体積の意味と考え方、柱体や錐体などの立体の体積の計算の仕方などについて説明します。
このページでは、「高さ」と言ったら断りのない限りは、底面から見た「立体的な意味での高さ」の事を意味しています。
立方体と柱体の体積
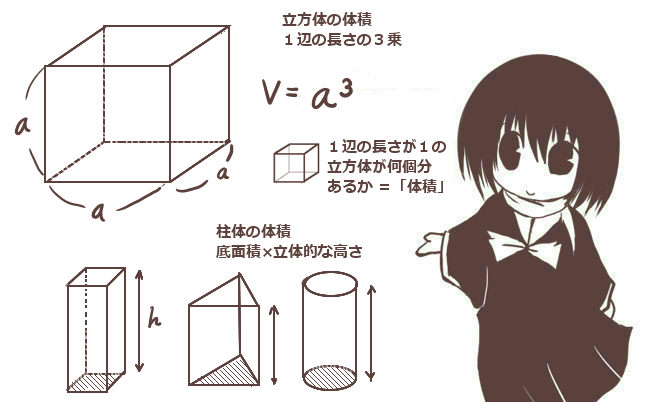
基本的には、1辺の長さが1の立方体の体積を1として、これが何個分あるかで立体の体積とします。それが2個分あれば体積は2、半分であれば1/2という具合です。面積が「広さ」を表す量であるのに対し、体積は大きさを表します。この時、1つの辺の長さが何倍かになれば、同じ割合で体積も増加します。
体積とは?
その意味で、1辺の長さがaの立方体の体積は、a3になります。例えば1辺が2であれば2×2×2=8が体積で、「1辺が1の立方体」の8個分の大きさであるという事です。
また、直方体の体積は互いに垂直な方向に伸びた3つの辺の長さの積になります。底面が辺の長さaとbの長方形で、立体的な高さがcである直方体の体積はa×b×c(=abc)となります。
体積の単位
3つの辺の長さが掛けられるので、その意味で辺の長さに単位がついている場合には、例えばセンチメートルcmに対しては体積の単位はcm3と書き、「立方センチメートル」と読みます。
単位がメートルであれば体積の単位はm3と書き「立方メートル」と読みます。
この時の単位の換算は、1m3=(100cm)3と考えて、1m3=1000000cm3(=106cm3)というふうにします。1立方メートルの体積は、100万立方センチメートルの体積に等しいという事です。これは、計算上の見かけはそうなるという事ではなくて、実際に立方メートルの体積の箱には1立方センチメートルのサイコロが100万個入る大きさであるという事です。
「え、そんなにたくさん入りますか・・?」
数字だけ見ると、確かにそんなに数が大きくなるだろうか?と、思ってしまいますね。しかし、100が100個あれば1万で、1万が100個あれば100万ですから、確かにそのような事になるのです。1cmのサイコロを1mの中に並べると、100個です。1mの長さの正方形には、それが100列ありますから1万個入ります。1mの長さの立方体には、それが100段ですから100万個になるという事です。身近な例で、計算してみると「意外と」大きくなるという例かもしれません。箱などの入れ物の体積を、特に「容積」と呼ぶ場合もありますが、数値として扱う時には体積と全く同じ単位や計算法を使います。
実用上の体積の単位として、「リットル」があります。記号ではℓ(「エル」の筆記体)を使います。【Lやl(小文字の「エル」)なども使われます。】これは牛乳などにも書いてある事もあるのでなじみがある人も多いかと思います。
実際、これは基本的には液体の体積を表すのに使われる事が多いものです。1リットルは、1000cm3に等しい体積です。液体の体積や、液体を入れる容器の体積を特に「容量」と言う場合もあります。
化学などでは「ミリリットル」という単位もよく使います。記号は、mℓもしくはmlのように書きます。この「ミリ」は、「1ミリメートル【mm】」のミリと同じで、千分の1という意味です。【10mmは1cmですが、本来は1m=1000mmという換算です。】
つまり、1000mℓ=1ℓですが、1ℓ=1000cm3でしたから、じつのところ1mℓと1cm3は、体積としては全く同じです。ただ、ミリリットルのほうは液体の容量を指す事が多いという点が実用上の違いです。
柱体の体積の考え方
面積の場合、三角形の面積は
三角形→平行四辺形→長方形→「正方形が何個分詰まっている広さか」
という考え方のもとで計算していました。立体の体積も、基本的に同じ考え方です。
まず、三角柱を考えると、これは2個合わせれば底面が平行四辺形である四角柱になります。その四角柱は、出っ張っている部分を切り取って反対側にくっつければ、直方体になります。
つまり、底面の三角形の面積を出して、立体的な意味での高さを掛ければ、体積1の立方体が何個分あるかという意味での体積に等しくなります。
さらに、任意の多角柱は、三角柱に分割できます。という事は、角柱の場合には
「底面の図形の面積(=底面積)」×「立体的な意味での高さ」
によって体積が計算できるという事を意味します。
円柱や、さらには任意の閉曲面を底面とする柱体でも考え方は同じで、無数の細かい三角柱の体積の和の極限を考えます。一般に柱体の体積は「底面積」×「立体的な意味での高さ」で計算します。
平行6面体のような立体の体積も、「底面×立体的な意味での高さ」で計算できます。底面に平行な平面で各高さの断面を見ると平行四辺形である事によります。【そのような薄い四角柱の合計の極限・積分として考えると導出は楽です。】
錐体の体積
三角錐、多角錐、円錐の体積の場合は、底面積×高さ÷3で計算します。(これを使った計算は、中学校の数学や高校入試の問題でも問われる事があります。)
体積=底面積×高さ÷3
この「÷3」あるいは「×1/3」は一体どこから出てくるのかというと、一番簡単な導出方法は積分を使う方法ですが、それを使わないでも導出は可能です。
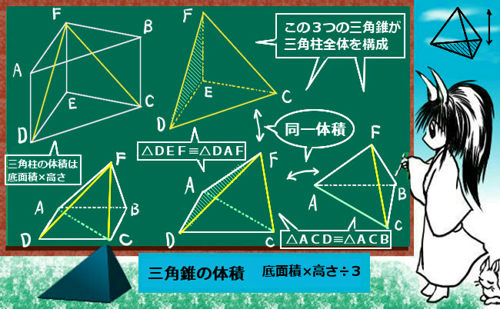
まず、三角錐からです。三角柱を考えて、これを体積が等しくなるように3分割する方法を考えます。この時に三角柱を、ちょうど体積が等しい三角錐3つで分割できます。三角柱の体積は「底面積×立体的な高さ」ですから、それを3で割って三角錐の体積になるというわけです。あるいは、三角錐を基準に考えるのであれば、「底面を共有し高さが等しく、かつ3倍の体積を持つ三角柱」を必ず考える事ができるので3で割ればよいというわけです。
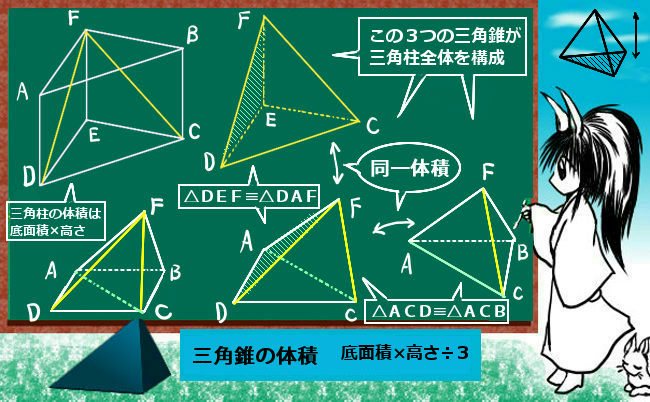
三角錐の体積については、底面積と立体的な意味の高さが分かっていれば、三角錐である限りどんな形状であっても公式を使えます。また、三角錐には4つの面がありますが、どの面を底面としても、そこから高さを測れば体積の公式を使えます。
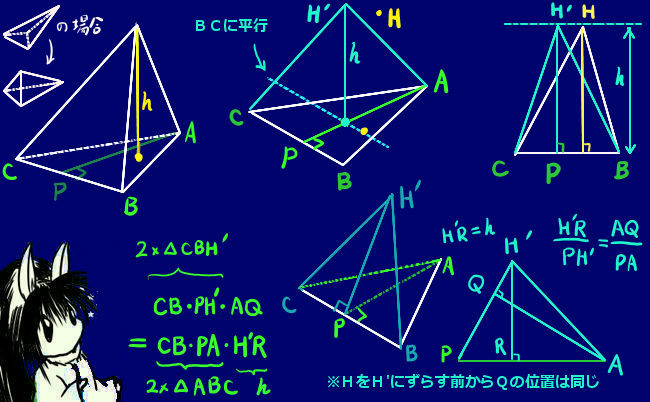
四角錐以上の多角錐は、全て底面を三角形の和として考える事ができます。そのため、多角錐の体積も同じく「底面積×立体的な高さ÷3」で計算できます。円も多角形で近似できるので、円錐の体積も同様になります。
柱体の時と同じ考え方で、多角錐と円錐についても同じく底面を三角形に分割して考えます。ただし四角錐以上の場合は、公式を使う時にどの面を底面として考えてもよいわけではなく、四角錐であれば四角形の面を、円錐であれば円の面を底面として、そこから高さを測ります。
球の体積については、図形だけから考えるのはかなり難しいので、積分によって体積の公式を出すのが普通です。結果は、半径をRとして(4/3)×R×円周率になります。