初等関数(英:elementary function)とは、大雑把に言うと「高校までに教わる関数」の事です。要するに、具体的には高校数学で扱っている関数が該当するのです。
例えば2次関数や、三角関数、それと指数関数と対数関数などが該当します。
目次:
★もう少し詳しく言うと「初等関数」とは、いわゆる高校で教わる関数の「加減乗除の組み合わせ」およびそれらの「合成関数」「逆関数」を指すとされますが、これはあまり気にしなくてよいでしょう。(ただし高校数学でも微積分までやる時は気にしてください。合成関数の微分や、逆関数の微分に対して特定の公式が成立するからです。)
初等関数は「特殊関数」に対する語でもあります。特殊関数とは具体的にはガンマ関数、ベータ関数、ゼータ関数のように積分や極限によって定義される関数が該当し、初等関数では表せない事を1つの特徴とします。
高校で教わる関数まとめ
さて、初等関数とは高校数学での関数と言い換えてもそんなに間違いはないので、初等関数とはどういうものかを見ると高校で教わる関数というものが見えてきます。
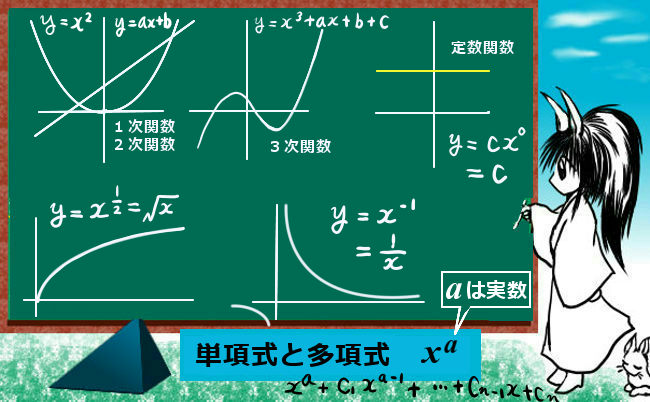
- 単項式と多項式:xaで表される関数。1次関数、2次関数、3次関数など。
反比例関数1/xや変数の平方根を考えた \(\sqrt{x}\) も含みます。 - 指数関数 実数等の「x乗」の形の関数。特に自然対数の底を使ったexが重要。
- 対数関数 ある数を何乗するとxになるかを表したもの。指数関数の逆関数でもある。
- 三角関数 直角三角形の辺の比をもとにした関数。代表的な周期関数としても使用。
- 逆三角関数 その名の通り三角関数の逆関数で、最近の高校ではあまり扱わない。微積分の理論においてむしろ使う事がある。
※他に例えば「双曲線関数」というものもありますが、これは指数関数の組み合わせで作る関数です。その他にも、初等関数を組み合わせて便宜上特別な名称をつける場合があります。ただし、高校数学ではそれらはさほど重要でない場合が多いです。
初等関数というものは、じつはまとめるとこれだけしかないのです。
もちろん、これらの組み合わせも初等関数であり、例えば1次関数と三角関数の組み合わせの xsin x なども該当します。また、高校ではこれらの関数の他に数列やベクトルや微積分や順列・確率等も教えますので、これら初等関数の一覧が高校数学の内容全てを網羅しているという意味ではありません。
しかしそれでも、高校で教わる具体的な関数というのは大別すると「じつはこれだけ」であるというのは少し意外であるという人もいるのではないでしょうか。高校数学でも、大学入試などでは確かに初見で時間内に正確に解くのはなかなか難しい「難問」や複雑な計算は存在しますが、それらも原則としてはじつは「基礎事項」の組み合わせなのです。
つまり学ぶべき基礎事項をしっかり整理して把握したうえで、それらを組み合わせて問題を解く練習をしてみる事が高校数学を得意にする鍵になります。
単項式と多項式
単項式とはxのa乗の形、つまりxaの単独の形です。
これらが和や差で組み合わさったx2+x+1などが多項式です。
xaのaを「指数」とも言います。単項式や多項式での指数の値は、高校数学では実数全体を取り得ます。
★高校数学および大学入試では、1次関数および2次関数について、図形上の性質と式による表現を組み合わせた出題がなされます。3次関数については微分によりグラフの形を考察するので、基本的には微積分での出題になります。
他方これらに対して、多項方程式を解くという作業は(中学校での)2次方程式の解法まででじゅうぶんです。3次方程式の解法や、4次方程式の解法は高校数学では原則として問われません。(ただしそれらを高校数学の範囲の知識で解く事は可能です。)
x0=1で、つまり定数関数は単項式に含めている形になります。
xaのaが負の値の時は分母に関数を持っていき反比例の形にしたものです。この時、x=0を定義域(変数xの値の範囲の事)から必ず除外して考えます。
$$x^{-1}=\frac{1}{x},\hspace{5pt}x^{-2}=\frac{1}{x^2}$$
xaのaが分数になる時は、自然数nを使って1/nの形になる時は「n乗根」(の正の値)を表します。この場合には、aがm/nのような形の時は、「xのm乗とxのn乗根の掛け算」であると考えます。
$$x^{\frac{1}{2}}=\sqrt{x},\hspace{10pt}x^{\frac{1}{3}}=^3\sqrt{x}$$
また、高校数学ではあまり気にする必要はないですがxaのaは無理数でもよくて、じつはさらに別途にaが複素数の場合も定義可能です。
こうしてみるとxの「何乗」の部分が自然数、負の数、有理数・・の場合があって複雑に見えるかもしれませんが、重要なのはそれらをxaという形で統一的な演算が可能であるという事です。
指数関数
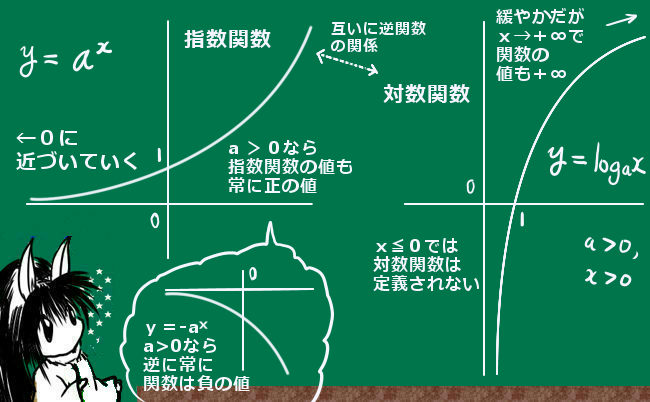
指数関数とは、2次関数や3次関数などとは異なり、「2のx乗」2xなどの関数です。基本的な考え方はxaの場合と同じで、指数関数2xなどの変数xの定義域は実数全体とする事ができます。
指数関数のグラフの形は、関数自体にマイナス符号がついていなければ正の値を常にとるという特徴があります。これは単項式や多項式で表される関数との大きな違いです。具体的な値を代入してみたりグラフに描いてみたりすると分かりやすいでしょう。
指数関数で重要なのは、e=2.718・・という無理数のx乗、exです。ただし、これが重要なのは微積分においてなので、もしも高校数学の範囲で微積分を除いて考えるのであればあまり気にしなくてよい事です。
対数関数
対数関数とは、指数関数の逆関数であり、logaxという記号で(正の数)aを「何乗するとxになるか」という値を関数とするものです。ここでのaの事を対数の「底」と言います。この時、x=aであれば logax=1, x=a2であればlogax=2です。
logaxにおいて、a=10の時を特に常用対数と言い、a=e=2.718・・の時を特に自然対数と言います。高校数学ではあまり気にしなくてよいのですが、常用対数を log x、自然対数を ln x(こちらをlog xとする人も)で記す場合があります。対数関数の場合、関数の値自体は負の数でもあり得ますが、変数の範囲は「正の数」という点がひとつ注意点です。
対数関数も指数関数と同じく、高校数学ではどちらかというと微積分との関連のほうが重要になってきます。
三角関数
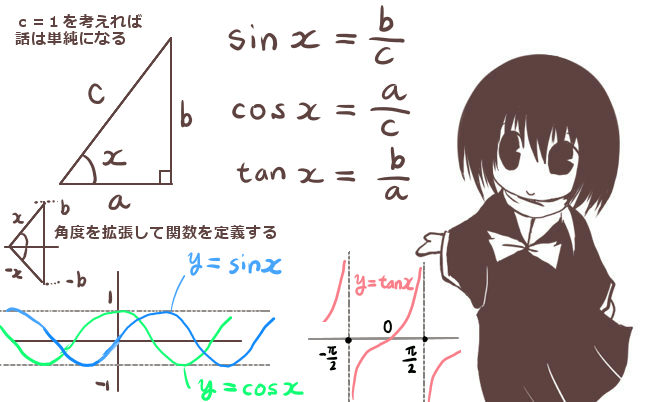
三角関数は、弧度法で表した三角形の角度を変数とした辺の比(三角比)を基本とする関数で、正弦関数(sin x)、余弦関数(cos x)、正接関数(tan x)の3つが基本です。角度を0から直角までに限定した場合して平面図形に使うなどには特に三角比と呼ぶ場合もあります。
必要に応じてこれらの逆数(例えば余接関数 cot x=1/(tanx))を考える事もありますが、高校数学では重要ではないでしょう。まず初めに学習すべき事を絞る事も大事である場合もあります。高校数学での基本は sin, cos, tan の3つだと思ってよいです。
三角関数は基本的には「角度」を変数とするのですが、プラスマイナスの値と対称性を考えて三角関数の変数の範囲は実数全体とします。(tan xだけは\(\pi\)/2 の奇数倍を定義域から除きます。)
前述の通り、逆三角関数については最近の高校ではほとんど問われないので、原則として気にする必要はありません。大学数学で扱う微積分の特定の計算で、逆三角関数を使う事が有用である場合があります。
以上、初等関数の一覧と重要な点を列挙しましたが、①:まずは学習すべき内容を整理し全体像をつかむ → ②:各関数についての細かい規定や計算方法を知る → ③:それらを組み合わせた問題(主に大学入試問題)を解く練習を積んでみる という手順が高校数学を得意にする勉強のやり方の1つです。
