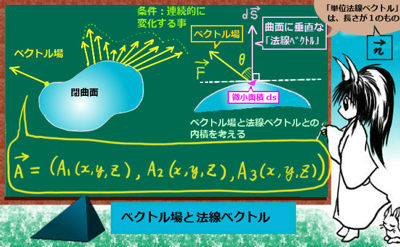
ベクトル解析と電磁気学の分野で使用する「法線面積分」は、閉曲面に分布するベクトル場に対して定義されるものです。ベクトル場とは、すなわちベクトルの3成分のいずれもがx、y、zのスカラー関数になっているベクトルです。
★書籍の紙面ではベクトルを表す表記として文字をボールド体にする方法が多く使われますが、このページではベクトルは一貫して文字の上に矢印を添える表記方法を採用します。
スカラー関数に対する「面積分」は似ていますが別物なので注意。具体的な計算方法も異なります。
ベクトルの内積の考え方を使用します。
法線面積分を表す式には幾つかの表記方法がありますが、次のようになります。いずれも等号で結ぶ事ができ、計算すれば同じ値になります。
$$\int_S \overrightarrow{F}\cdot d\overrightarrow{s}=\int_S (F_1 ds_1 + F_2 ds_2 + F_3 ds_3)=\int_SF_1 ds_1+\int_SF_2 ds_2+\int_SF_3 ds_3$$
$$\overrightarrow{F}=(F_1(x,y,z),F_2(x,y,z),F_3(x,y,z))$$
$$\int_S \overrightarrow{F}\cdot d\overrightarrow{s}を、\int_S \overrightarrow{F}\cdot \overrightarrow{n}dsとも書きます。$$
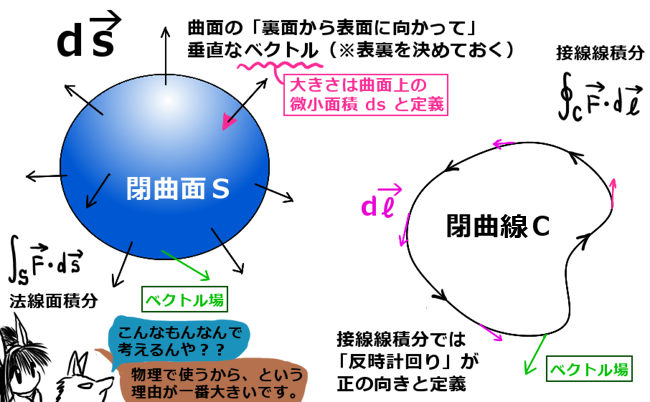
積分記号に添えてあるSは、surface(表面)からの記号として一般的に使われる記号です。
特定の閉曲面の表面全体(表側あるいは裏側のいずれかの全体)を表します。
また、二重積分で表して計算する事も可能です。その場合、各項の具体的な計算をする時には2方向の積分区間をきちんと指定します。 $$\int_S \overrightarrow{F}\cdot d\overrightarrow{s}=\int\int_S (F_1 dydz + F_2 dzdx + F_3 dxdy)$$ $$=\int_{Y1}^{Y2}\int_{Z1}^{Z2}F_1 dydz+\int_{Z1}^{Z2}\int_{X1}^{X2}F_2 dzdx+\int_{X1}^{X2}\int_{Y1}^{Y2}F_3 dxdy$$
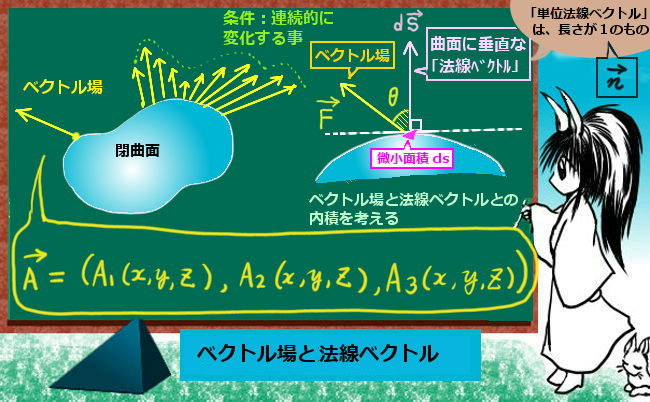
\(\overrightarrow{n}\) は、曲面の各点に対する単位法線ベクトルを表し、長さは1で曲面に対し垂直な向きのものです。また、\(d\overrightarrow{s}=ds\overrightarrow{n}\) になります。詳しくは次のようになります。
$$ d\overrightarrow{s}=( ds_1 , ds_2 , ds_3 ) $$
$$|\overrightarrow{n}|=1,\hspace{10pt}|d\overrightarrow{s}|=ds=\sqrt{ds_1^2 + ds_2^2 + ds_3^2},\hspace{10pt}d\overrightarrow{s}=ds\overrightarrow{n}$$
\(d\overrightarrow{s}\) および単位法線ベクトル\(d\overrightarrow{n}\) は、閉曲面上の各点から曲面の「裏側→表側」に向かう向きに伸びると約束します。
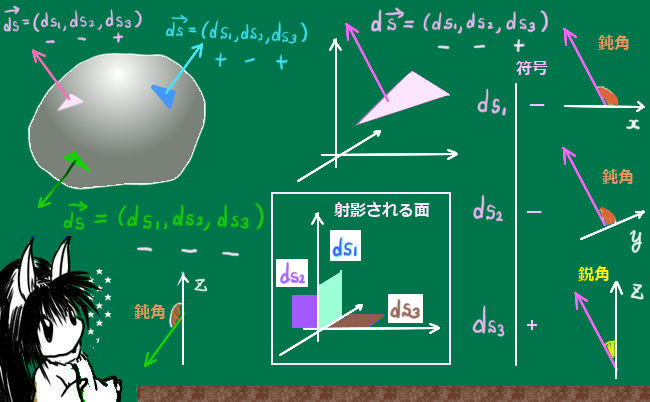
各成分は、微小面積の平面への「射影」になっています。
- \(|ds_1| \)=「yz平面」への射影領域の面積
- \(|ds_2| \)=「xz平面」への射影領域の面積
- \(|ds_3| \) =「xy平面」への射影領域の面積
外積ベクトルの成分の大きさ(絶対値)はyz平面、xz平面、xy平面への三角形の射影の面積に等しくなりますから、\(d\overrightarrow{s}=( ds_1 , ds_2 , ds_3 )\) の各成分の大きさも、垂直な3つ平面への微小面積の射影面積に等しくなる事が示されます。
法線ベクトルの成分ds1、ds2、ds3には通常のベクトルと同じく符号があります。
式としては、法線ベクトルと射影平面に垂直な軸がなす角の余弦の符号と同じプラスマイナスの符号を持つと定義します。例えば、ds1であれば対応する射影平面がyz平面で、それに垂直な軸はx軸ですから、法線ベクトルとx軸がなす角を見ます。それが鋭角であればds1の符号は+で、鈍角であれば-の符号になります。その符号は、座標上の図に描いてみた時の向きから判定したものともちろん一致します。
図で状況を見ながら式の意味を考えると分かりやすいでしょう。
つまり、球面などの閉曲面の各点にベクトル場がぎっしり詰まっている感じです。それを曲面全体に渡って積分します。その際に、ベクトル場の「曲面の法線ベクトルの向きの成分だけ」を内積によって取り出したものを考えているわけです。
微小面積を大きさに持つ法線ベクトル\(d\overrightarrow{s}=ds\overrightarrow{n}\)と微小面積の射影面積との関係も、図に描いて外積ベクトルとして捉えると見通しがよいです。
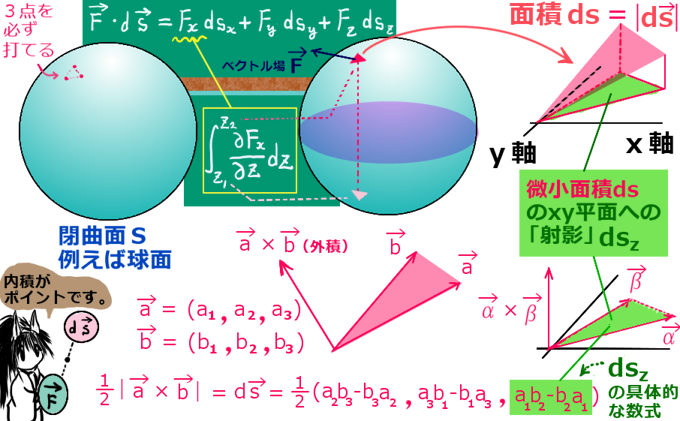
法線ベクトル\(d\overrightarrow{s}\)の成分の符号については、個々の法線ベクトルについて例えば(-1,2,1)といった成分表示となる事からプラスマイナスの符号を持ちます。各成分の「大きさ」については、微小面積のyz平面、xz平面、xy平面への射影面積に等しくなるという事です。
積分内の内積の部分については、余弦を使ったほうの内積の定義として書く場合もあります。
$$\overrightarrow{F}\cdot d\overrightarrow{s}=|\overrightarrow{F}||\overrightarrow{s}|\cos \theta$$
ただし、電磁気学などで法線面積分を考える場合では、特別な形のモデルで最初から考える場合も多いのです。例えば、ベクトル場が曲面に全て垂直であれば公式を使わなくても角度は0とすぐに判断できて、余弦は1になります。