今回は「特性方程式 」という多項方程式を解く事で、
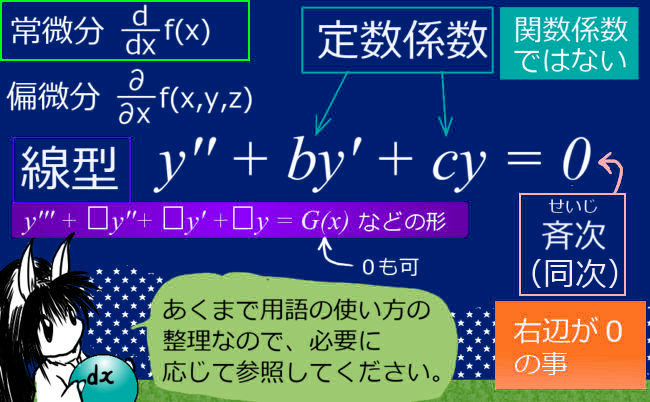
この方法で解けるのは「定数係数」で「線型」の「常微分」の微分方程式です。「1階微分=ゼロ」「2階微分」=ゼロ」といった簡単に解ける微分方程式 はその仲間です。それらの解法の延長線上・発展事項として今回の内容があります。n階の定数係数の線型常微分方程式の数学的な一般的解法を、この記事では詳しく見ていく事になります。
式が少し込み入る計算も含みますが、今回の内容で必要な公式は微積分の基本公式だけです。一部、複素関数論や代数学の話も含まれますが、そこは参考までに眺めるだけでも差し支えない箇所です。
「定数係数の線型常微分方程式」・・というのは名称が長いので、今回の記事の内容に限っては「常微分」であることや「線型」である事は前提として、単に「微分方程式」と記す事もあります。
今回扱うのは、一般のn階の「定数係数」の「線型」常微分方程式です。 (その中でもさらに「斉次」 のものです。ただし、非斉次のものも変形して斉次として扱える場合があります。)
「特性方程式」とは?
n階の定数係数の線型常微分方程式について、それぞれの階数の微分の部分に定数係数がくっついているわけですが、この時に次の対応を考えます:
$$n階微分の項に対する定数係数c_n \hspace{10pt} → \hspace{10pt} c_nx^n【定数項はそのまま定数項に対応】$$
この対応で作る多項方程式を、 定数係数の線型常微分方程式の特性方程式 と言います。
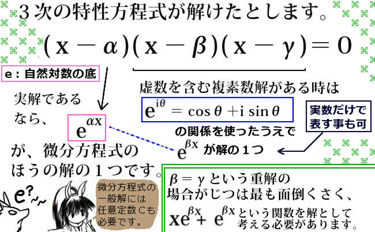
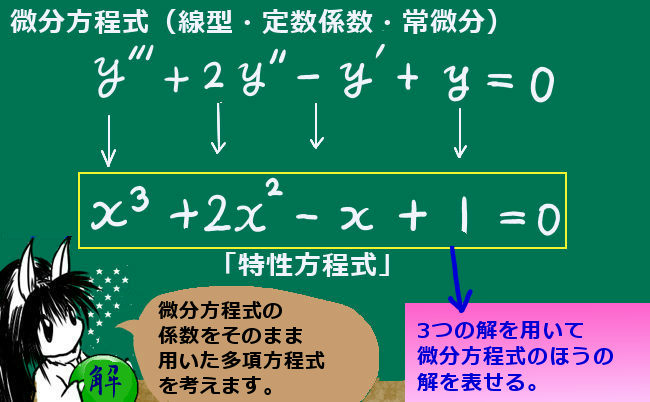
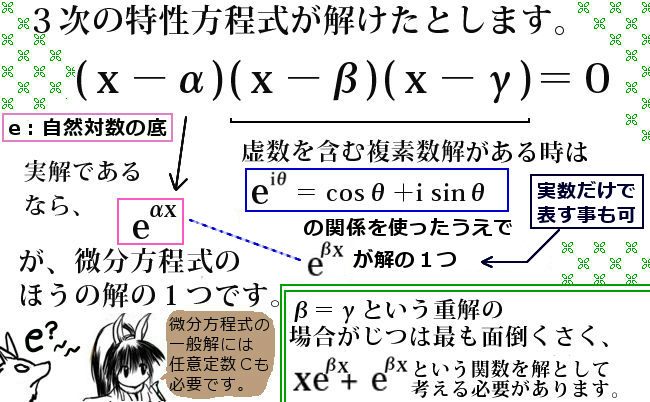
具体的な3次の例で見てみますと、次のようになります。
$$微分方程式:y^{\prime \prime \prime }+3y^{ \prime \prime }-2y^{\prime }+1=0$$
$$対応する特性方程式:x^3+3x^2-2x+1=0$$
一般のn次の特性方程式は次のようになります。
n次の特性方程式
次のような
$$x^n+c_{n-1}x^{n-1}+c_{n-2}x^{n-2}+\cdots+c_3x^3+c_2x^2+c_1x+c_0=0$$
の事を、その微分方程式に対する
特性方程式 (characteristic equation)と言います。
特性方程式の解の事を「特性根」と言う事もあります。
このように具体例で見たほうが分かりやすいかもしれませんね。
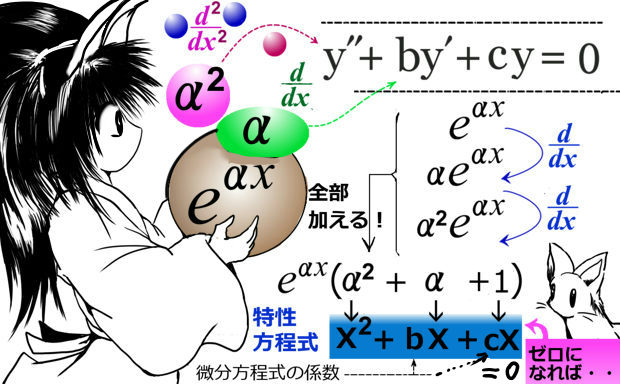
このように、作り方自体は簡単です。じつは特性方程式の「解」が、微分方程式のほうの解に直接関係します。根底にあるのは、自然対数の底 e の指数関数の微分演算です。微分して得る導関数が元の関数と同じであり、合成関数の微分を利用すると「元の関数×定数倍」という形を作れます。このパーツを上手に利用する事で、一般的には特性方程式とその解を計算すればよい、という理論になるのです。
用いる微積分の基本公式は、自然対数の底 e の指数関数と合成関数の微分公式です。それと積の微分公式も使用します。
対象の関数 微分公式 微分方程式の解法での役割 自然対数の底 e の指数関数 \({\large \frac{d}{dx}e^x=e^x}\) 微分すると元の関数に戻る 合成関数の微分 \({\large \frac{df(y)}{dx}=\frac{df(y)}{dy}\frac{dy(x)}{dx}}\) 微分方程式内の定数倍などを調整 積の形の微分 \({\large \frac{d}{dx}(fg)=\frac{df}{dx}g+\frac{dg}{dx}f\frac{dy(x)}{dx}}\) このページで解説する証明で使ったりします。
微分してない、もとの関数:\(e^{\alpha x}\)
微分1回目:\(\frac{d}{dx}e^{\alpha x}=\alpha e^{\alpha x}\)
微分2回目:\(\frac{d^2}{dx^2}e^{\alpha x}=\alpha^2 e^{\alpha x}\)
2階の場合の定数係数の微分方程式と、2次の特性方程式の関係が一般のn次の場合の解法の基本になりますので次に詳しく解法を見ます。
これは2次の特性方程式(多項方程式としては2次方程式)が異なる2つの実数解を持つ場合ですね。ただし、特性方程式が重解や複素数解を持つ場合でも、e の指数関数が重要である点には変わりありません。
2次の特性方程式が複素数解を持つ場合
2次の特性方程式が「異なる2つの実解」を持つ場合 は、自然対数の底 e の指数関数を用いればよい事を、
「じゃあ、そうでない場合はどうするのですか。」
まず、解が複素数解(虚数単位 i を含む解)である場合を述べます。この場合のほうがじつは比較的簡単です。解の表現としては虚数単位 i を含む形と、含まない形の両方で表現可能です。任意定数として複素数も許容されるとする事によって、定数をてきとうに調整すれば両者は同等になります。2つの形を両方記しておきましょう。
2次の特性方程式が複素数解である場合の微分方程式の解
2次の特性方程式の解が \(x=A+Bi\) である時、
対応する微分方程式の解 y は次のように表されます:
$$①虚数単位iを含む形で表す場合:y=C_1e^{\alpha x}+C_2e^{\beta x}$$
$$②実数でのみで表す場合:y=C_1e^{Ax}\cos (Bx)+C_2e^{Ax}\sin (Bx)$$
$$C_1とC_2は任意定数【特に①の場合、複素数も含めた任意定数です。】$$
①の形は、特性方程式の解が異なる2つの実数解である場合と同じ形です。①と②の2つの形が同等である事の詳細は後述しますが、複素数も含めた任意定数を上手に調整する事で示します。実数のみで表す事も可能である事から、物理の古典力学の範囲でも普通に意味を持つ事が見えるかと思います。
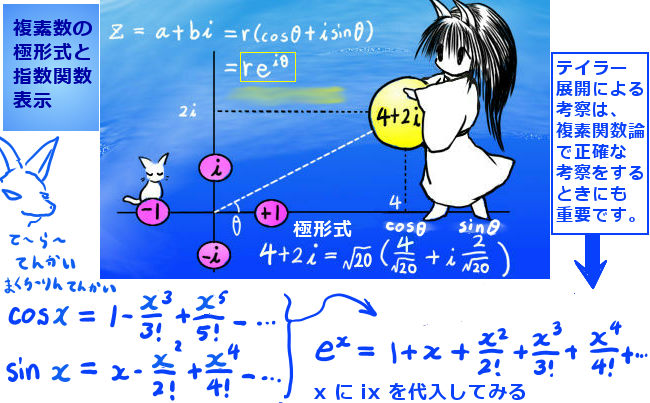
複素数を r(cosθ+i sinθ) という「極形式」で表したうえで、 r(cos(θx)+i sin(θx)) という関数を考えてみます 。【このように複素数を含んだ関数を、数学上は複素関数とも言います。】
この形の関数は、じつは微分した時に、e の指数関数と同じ性質を持っています。
$$\frac{d}{dx} r(\cos( \theta x)+i \sin( \theta x)) = r\theta (-\sin ( \theta x) +i\hspace{5pt}\cos ( \theta x) )=i \theta r (\cos( \theta x)+i \sin( \theta x)) $$
$$微分した後の式変形では、i^2=-1という関係を使っています。$$
【r等も変数ならxで偏微分という事になりますが、ここではr等は定数としてxでの「常微分」です。】
この結果を注意して見ていただくと、 xについてのもとの関数を「iθ 倍」したものと同じです。これは e の指数関数と同じ性質であり、指数関数の変数として複素数も考えるとするとじつは次のように書けます:
ポイントとなる1つの関係式
$$re^{i\theta x}= r(\cos( \theta x)+i \sin( \theta x)) $$
$$(おおもとの形:e^{i\theta}=\cos \theta +i\sin \theta)$$
この関係式は、ある条件(※)をつける事によって、変数が複素数範囲の場合は本質的にこの形として表してよいというものです。【(※):複素関数が「正則関数」であるという条件です。】
形式的には、e の指数関数のマクローリン展開(x=0でのテイラー展開)に、xの代わりに「 ix を代入してみて」、そこに正弦と余弦のマクローリン展開を「代入」する事で複素数の「指数関数表示」を得ます。ただし、より正確には複素数変数の指数関数を新たに定義するか、正則関数としての指数関数の複素数領域への拡張はただ1通りしかないという論法で指数関数表示を考察します。
この事を踏まえて、微分方程式 y”+ay’+by = 0 の解を考察します。
$$e^{\alpha x}=e^{(A+Bi)x}=e^{Ax}e^{Bi}x$$
これを、xで微分してみましょう。
$$\frac{d}{dx} e^{\alpha x}= \frac{d}{dx} ( e^{Ax}e^{iBx})=Ae^{Ax} e^{iBx} +iB e^{Ax} e^{iBx} =(A+Bi) e^{Ax} e^{iBx} = (A+Bi) e^{\alpha x}=\alpha e^{\alpha x} $$
このように、積の微分公式を使って丁寧に計算すると、微分の演算は実数係数の場合と全く同じ形になる事が分かります。 これは結局のところ、指数関数の部分が係数が乗じられる以外には形が変化しない事に起因しています。
と、なると解が異なる2つの実数ではなくて複素数であったとしても、
$$解は y=C_1e^{\alpha x}+C_2 e^{\beta x}の形で表せるという事です。 $$
微分方程式のほうの解を実数だけで表す方法
さて、前述のようにじつはこれを実数だけで表す事も可能です。
$$さきほどのe^{\alpha x}=e^{(A+Bi)x}=e^{Ax}e^{Bi}xという関係を使いましょう。ここで\beta=A-Biである事は重要です。$$
$$y= C_1 e^{Ax}e^{Bi}x +C_2 e^{Ax}e^{-Bi}x = C_1 e^{Ax} (\cos (Bx)+i\sin (Bx))+ C_2 e^{Ax} (\cos (Bx)-i\sin (Bx)) $$
$$= (C_1+C_2) e^{Ax} \cos (Bx) +i e^{Ax}\sin(Bx)(C_1-C_2)$$
$$C_1+C_2=C_3, C_1-C_2=iC_4 とすると、【そのようにおいてもよい事に注意】$$
$$y= C_3 e^{Ax} \cos (Bx) +C_4e^{Ax}\sin(Bx) $$
このように、任意定数も複素数であってよい事から「i を消せる」のです。特性方程式の2つの解が(必ず)共役複素数である事により、このように計算できます。
特性方程式の解(特性根)が異なる実数解の場合と複素数解の場合とでは、同じ形として微分方程式のほうの解を表す事が可能です。
2次の特性方程式が重解を持つ場合
次に、2次の特性方程式が重解(必ず実数)を持つ場合です。
2次の特性方程式が重根を持つ場合
特性方程式の解(重解)を \(\alpha\) とすると
$$y=C_1e^{\alpha x}+C_2xe^{\alpha x}=e^{\alpha x}(C_1+C_2x)$$
「x が指数関数に乗じられる」という形の項が、オマケでくっついてくるわけです。
\(e^{\alpha x} \) にxの1次関数が乗じられていると考える事もできます。
この解は、実際に微分してみると確かに微分方程式を満たす事は割と簡単に分かりますが、パっと見では2番目の項も含まれる事は、なかなか気づかないと思います。そこで、この解の詳しい導出について見ておきましょう。
$$演算子として\hat{D}=\left(\frac{d}{dx}-\alpha\right) を定義しておきます。 \hat{D} y= \frac{dy}{dx}-\alpha yです。$$
$$ \hat{D}^2=\hat{D} (\hat{D}) と定義すると \hat{D}^2= \left(\frac{d^2}{dx^2}-2\alpha \frac{d}{dx} +\alpha ^2\right) です。$$
$$\hat{D}^2y= \frac{d^2y}{dx^2}-2\alpha \frac{dy}{dx} +\alpha ^2y $$
この記号は別に定義しなくても証明はできますが、計算が結構煩雑なので過程を詳しく見るのに役立ちます。これはあくまで、ここでの計算だけに適用する便宜上の記号です。
特性方程式が重解を持つという設定ですから
$$x^2+Ax+B=(x-\alpha)^2= x^2-2\alpha x +\alpha^2より、 A=-2\alpha,B=\alpha^2$$
$$よって、y^{\prime\prime}+Ay^{\prime}+By= y^{\prime\prime} -2\alpha y^{\prime}+ \alpha^2 y= \hat{D}^2y$$
$$特性方程式が重解を持つならば、 y^{\prime\prime}+Ay^{\prime}+By=0 \Leftrightarrow \hat{D}^2y =0 という事です。$$
$$ここで、\hspace{5pt}e^{-\alpha x}y \hspace{5pt} という関数を考えると話がうまく進みます。$$
これの1階微分は、単純に積の微分公式を用いて計算を進められます。
$$\frac{d}{dx}(e^{-\alpha x}y)=-\alpha e^{-\alpha x}y+e^{-\alpha x}(y^{\prime})=e^{-\alpha x} \left (\frac{d}{dx}-\alpha \right)y$$
2階微分も積の微分公式を用いて計算を進められます。
$$\frac{d^2}{dx^2}(e^{-\alpha x}y)=\frac{d}{dx}\left\{e^{-\alpha x}\left(\frac{d}{dx}-\alpha \right )y\right\}=-\alpha e^{-\alpha x} \left (\frac{d}{dx}-\alpha \right )y+e^{-\alpha x}\frac{d}{dx}{\left(\frac{d}{dx}-\alpha\right)y}$$
$$= e^{-\alpha x} \left \{ -\alpha (\hat{D}y) + \frac{d}{dx}(\hat{D}y)\right \}= e^{-\alpha x} \left\{\left(\frac{d}{dx}-\alpha \right ) (\hat{D}y)\right\} = e^{-\alpha x} \hat{D}^2y $$
$$※ \left(\frac{d}{dx}-\alpha \frac{d}{dx} \right )y=\hat{D}y が1つの塊であり、 e^{-\alpha x} とのつながりは「通常の掛け算」である事に注意。$$
$$すると、 \hat{D}^2y =0 ならば e^{-\alpha x} \hat{D}^2y つまり \frac{d^2}{dx^2}(e^{-\alpha x}y)=0です。$$
$$ \frac{d^2}{dx^2}(e^{-\alpha x}y)=0 という形は、「2階微分=0」という形の微分方程式です。$$
「2階微分=0」という形の微分方程式の解は1次関数です。
$$「特性方程式が重解を持つ」 \Rightarrow y^{\prime\prime}+Ay^{\prime}+By=0 \Leftrightarrow \hat{D}^2y =0 \Rightarrow \frac{d^2}{dx^2}(e^{-\alpha x}y)=0 $$
$$ \Rightarrow e^{-\alpha x}y =C_1x+C_2 \Leftrightarrow y= e^{\alpha x}(C_1x+C_2)[証明終り]$$
最後の式変形は、両辺に\(e^{\alpha x}\)を掛けただけです。
n階の定数係数の線型常微分方程式の解法
さて、以上で2階の場合の考察を見てみましたが、3階以上の場合も基本的な考え方は同じです。ただし、3次以上の場合の特性方程式は実数解と複素数解が両方含まれている事もあり、実数解の場合は重解かそうでないかにも分かれます。
特性方程式が「解けた」という前提のもとで話を進めるとすると、その解を用いて微分方程式のほうの係数を表せます。表記を簡単にするため、4階のものを例に考えます。上記で、特性方程式の解が重解の場合に用いたような演算をここでも行います。
$$\frac{d^4y}{dx^4}+A_3 \frac{d^3y}{dx^3} +A_2 \frac{d^2y}{dx^2} +A_1 \frac{dy}{dx} + A_0y=\left(\frac{d}{dx}-\alpha_1\right) \left(\frac{d}{dx}-\alpha_2\right) \left(\frac{d}{dx}-\alpha_3\right) \left(\frac{d}{dx}-\alpha_4\right)y $$
$$A_3=\alpha_1+\alpha_2+\alpha_3+\alpha_4, A_0=\alpha_1 \alpha_2 \alpha_3 \alpha_4 等が成り立っています。 $$
1つ1つの解が「異なる実数解」や複素数解であれば2階の時と考え方は全く同じで、それらの解と e の指数関数を組み合わせ、任意定数とも合わせて加え合わせる(これを「線型結合」と呼びます)事を考えればよいのです。
$$つまり、C_1e^{\alpha_1 x}+ C_2e^{\alpha_2 x} + C_3e^{\alpha_3 x} + C_4e^{\alpha_4 x} などが解になります。$$
複素数解の部分は、2階の時と同じく実数だけで表す事もできます。共役になってる2解を用いて、指数関数と三角関数の積で表せます。(n次方程式の場合も、複素数解がある場合は必ず共役なもの同士が2つ1組になっています。)
$$例えば\alpha_1 と\alpha_2が共役な複素数解なら、\alpha_1=A+Bi, \alpha_2=A-Bi として$$
$$C_1e^{\alpha_1 x}+ C_2e^{\alpha_2 x}の部分をe^{Ax}(C_a\cos (Bx)+C_b\sin (Bx) )に変えても同じです。$$
「では、重解が含まれていたらどうなるのですか?」
n階の場合も、面倒なのは重解を持つ場合です。この場合、3重解4重解・・などを持つ事もあり得るので、考え方は2階の時と似ていますが別の補題を証明する必要があります。
補題
$$任意の自然数nに対して、
\frac{d^n}{dx^n}(e^{\alpha x}y)=e^{\alpha x}\left\{\left(\frac{d}{dx}+\alpha\right)^ny\right\}$$
$$ここで、\left(\frac{d}{dx}+\alpha\right)^nは\left(\frac{d}{dx}+\alpha\right)^2=\left(\frac{d}{dx}+\alpha\right)\left(\frac{d}{dx}+\alpha\right)=\left(\frac{d^2}{dx^2}+2\frac{d}{dx}\alpha+\alpha^2\right) 等の事。$$
これは、数学的帰納法を用いて丁寧に計算すると証明できます。
まず、n=1の場合は積の微分公式を用いてるだけで、これは成立します。
あるnで成立するとして、n+1の場合を考えます。
$$\frac{d^{n+1}}{dx^{n+1}}(e^{\alpha x}y)=\frac{d}{dx}\left\{\frac{d^n}{dx^n}(e^{\alpha x}y)\right\}= \frac{d}{dx}\left[ e^{\alpha x}\left\{\left(\frac{d}{dx}+\alpha\right)^ny\right\}\right]$$
$$=\alpha e^{\alpha x}\left\{\left(\frac{d}{dx}+\alpha\right)^ny\right\} + e^{\alpha x} \frac{d}{dx}\left[ \left\{\left(\frac{d}{dx}+\alpha\right)^ny\right\}\right] $$
$$= e^{\alpha x} \left( \frac{d}{dx} +\alpha\right) \left\{\left(\frac{d}{dx}+\alpha\right)^ny\right\} = e^{\alpha x} \left\{\left(\frac{d}{dx}+\alpha\right)^{n+1}y\right\} $$
よって、n+1の時も成立しますので任意の自然数nで成立します。【補題の証明終り】
さて、この補題を使ってどのように微分方程式のほうの解を考えるかと言いますと、次のようになります:
$$例えば N 重解になる部分について微分方程式を \left(\frac{d}{dx}-\alpha\right)^ny=0 と表せますから、 $$
$$ \left(\frac{d}{dx}-\alpha\right)^ny=0 \Rightarrow e^{-\alpha x} \left(\frac{d}{dx}-\alpha\right)^ny=0 \Rightarrow \frac{d^n}{dx^n}( e^{-\alpha x}y)=0$$
【※プラスマイナスの符号が上記補題と入れ替わるので注意してください。\(\alpha\) を \(-\alpha\) に置き換えます。】
$$つまり「e^{-\alpha x}yという関数をn回微分すると0になる」という式になります。$$
1回微分して0になる関数は定数関数、2回微分して0になる関数は1次関数であるわけですが、n回微分して0になる関数は(n-1)次関数です。
$$よって、 e^{-\alpha x}y =x^{n-1}+C_{n-2}x^{n-2}+\cdots+C_2x^2+C_1x+C_0$$
$$\Leftrightarrow y= e^{\alpha x}( x^{n-1}+C_{n-2}x^{n-2}+\cdots+C_2x^2+C_1x+C_0 )という事になります。$$
指数関数に(n-1)次関数を乗じた形の解になります。2次の特性方程式が重解を持つ時には指数関数に1次式を乗じた形の解であったわけですが、それもこのn次の場合の解の形に含まれるわけです。
$$特性方程式の解が3重根であれば、微分方程式のほうの解はy= e^{\alpha x}( C_2x^2+C_1x+C_0 ) になります。$$
この特性方程式の重解の部分に対する微分方程式のほうの解を、異なる実数解や複素数解に対応する微分方程式の解に加え合わせて、全体の一般解になるわけです。
参考:n次方程式について 複素数係数のn次方程式は、m重解の部分をm個の解と数えると約束するうえで、n個の複素数解(実数解を含めて)を必ず持ちます。これは代数学の基本定理と呼ばれます。(代数学の「基本」となる定理なのかは別問題ですが・・。)
特性方程式による、常微分方程式の解法についての考察
以前考察した簡単な微分方程式の解法について、特性方程式の観点からまとめと考察をしてみます。
■ 解法のまとめと一覧表 ■ 解法の考察 (特性方程式の観点から)
解法のまとめ・・一覧表
1階と2階の定数係数の線型常微分方程式を例にして、5つのタイプの微分方程式をまとめてみます。
微分方程式
解
使用する微分公式
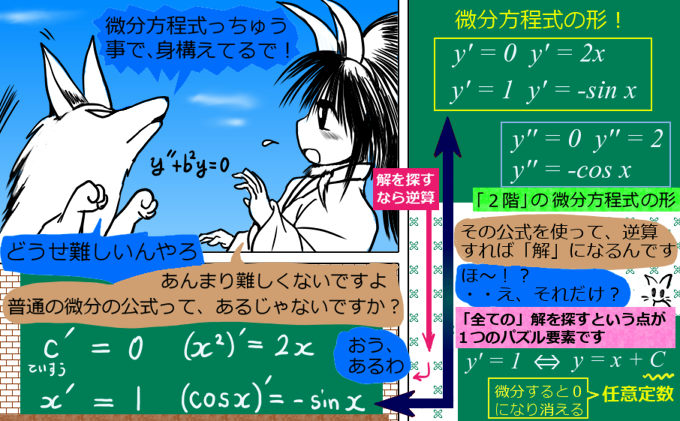
① \(y^{\prime}=0\)
\(f(x)=C\)
定数関数の微分
② \(y^{\prime\prime}=0\)
\(f(x)=bx+C\)
単項式の微分
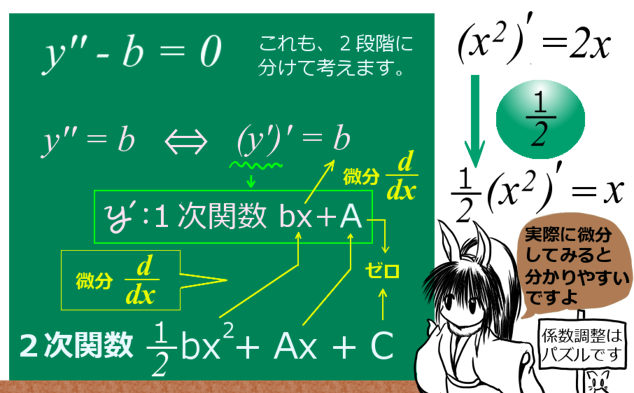
③ \(y^{\prime\prime}-b=0\)
\(f(x)=\frac{b}{2}x^2+Ax+C\)
単項式の微分
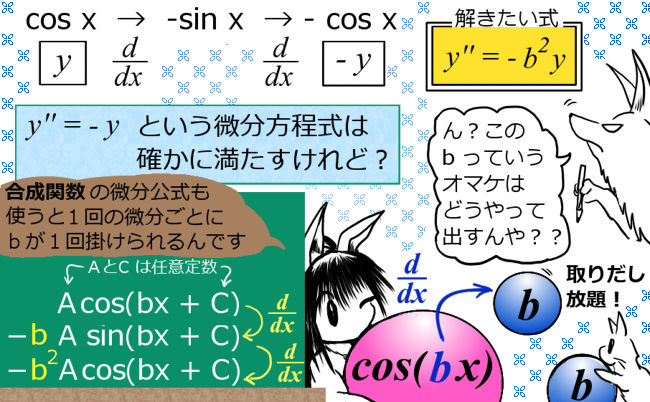
④ \(y^{\prime\prime}+b^2y=0\)
\(f(x)=A\cos (bx+C)\)
三角関数と合成関数の微分
⑤ \(y^{\prime\prime}+by^{\prime}+cy=0\)
1.特性根\(\alpha,\beta\)が重解でない:
これがこのページで特に扱った内容です。特性根が重解で無い場合は、実数解と複素数解の場合をまとめています。
「特性根 」とは、「特性方程式の解」の事です。
解法の考察・・特性方程式の観点から見ると?
上記の5つの種類の解は、5番目のタイプで「特性方程式の解」が重解である場合と複素数解である場合を含めると、③タイプを除いて「数学的にまとめる」事も可能なのです。
どういう事かと言いますと、まず④の三角関数タイプは、じつは特性方程式の観点から言うと「特性根として複素数解」を持つ場合なのです。その場合、e の指数関数は複素数と三角関数の関係により表され、任意定数(複素数も可)を上手に選ぶと「実数範囲の三角関数」を解として得る事ができます。特性方程式が複素数解を持つ場合には、解を複素数でも実数でも表せる事を上記で述べましたが、その事です。
①②の、定数関数と1次関数が解のパターンは、ちょっと意外かもしれませんが、特性方程式の観点からは、じつは「特性根が重解」パターンの仲間なのです。(上記では最も面倒だったパターンですね。)ただ、「2階微分=0」のような場合には特性方程式の重解は 0 ですので、指数関数部分は1となって見えなくなるので、定数の場合も含めて1次関数の部分だけが残ります。そのような見方も数学的には可能という事です。
上の表の中でじつは仲間外れなのは③の2次関数タイプで、定数係数の常微分方程式の中で、これだけが「非斉次」タイプで、残り①②④⑤は「斉次」タイプなのです。このページで扱った内容(表の中では⑤)は、全て「斉次」のものです。そのために、③の解だけは⑤の枠組みとは少し違ったものになっている、という見方もできるわけです。(※ただし、非斉次であっても一工夫して斉次の形に変形をしたうえで解く事は可能です。)