円・扇形に関連する面積の計算

円と扇形の面積に関連する計算の数学・算数の問題について説明します。

円と扇形

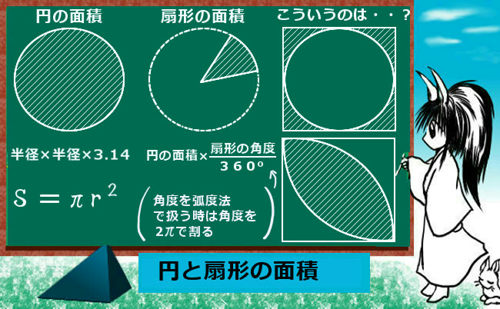
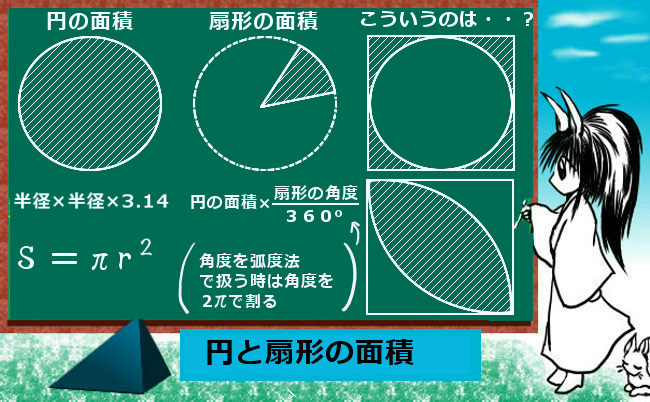
まず、円の面積は半径の２乗と円周率（≒３.１４）の積です。

例えば、半径が２メートルの円の面積はおおよそ２×２×３.１４＝１２.５６平方メートルという事です。

他方、「扇形」とはピザやアップルパイのように、中心からまっすぐ円周に向かって円を切り取った部分のような形の図形の事です。

この扇形の面積を計算するには、角度を使います。要するに角度が全体の何割かという事で、面積が円全体の何割かという事で計算するわけです。

例えば、簡単な例では半円は円の半分の面積、１／４円の面積は円の１／４の面積です。６０°の角度の扇形の面積は円の１／６の面積になります。

円・扇形に関する面積の応用問題

さて、算数や中学数学での図形の問題で、円や扇形に関連する「変な形」の図形の面積を計算させる問題があります。例えば、四角形から円を切り取った部分の面積や、１／４の円を組み合わせて作ったラグビーボールのような図形の面積です。

基本的には、ある図形の面積から別の図形の面積を差し引き、それをうまく組み合わせて変な形の図形の面積を上手に計算するのです。

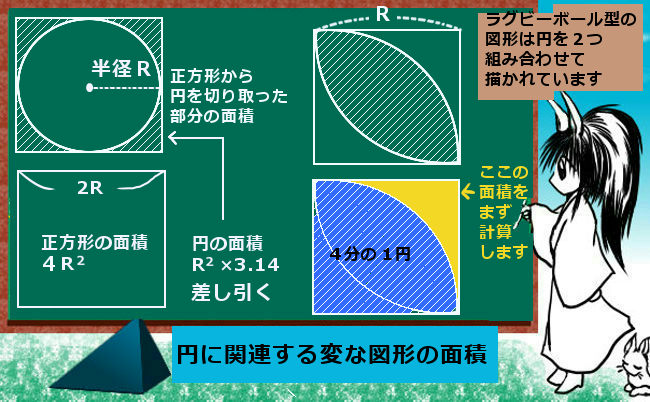
例えば、１辺の長さが２Ｒである正方形を考えましょう。これに円が内接する場合、円の半径はＲになります。そこで、正方形から円の部分を切り取った図形（４つ分）の面積は次のようになります。

$$S=(2R)^2-R^2×3.14=(4-3.14)R^2=0.86R^2$$

Ｒ＝１で正方形の１辺が２で正方形の面積が４である場合、約０.８６が切り取られた部分の面積の合計というわけです。１部分の１つだけの面積を問う問題であればそれをさらに４で割ります。

ラグビーボール型の面積については、２段階を踏みます。
今度は円の半径が正方形の１辺に等しいのでこれをＲとしましょう。

まず、正方形から４分円（円の４分の１）を引きます。

そして、その部分の２倍を、正方形から引きます。
これがラグビーボール型の図形の面積になります。

$$S=2×(R^2-R^2×3.14÷４)=2×0.215×R^2=0.43R^2$$

Ｒ＝１であればラグビーボール型の図形の面積は約０.４３という事になります。

この手の問題は図形の組み合わせによっていくらでも複雑にできるところがありますが、基本的にはこのように公式で面積が分かる図形から切り取った図形を組み合わせて計算します。

中学数学の場合は、三角形との組み合わせの問題もあり得ます。例えば、三平方の定理や図形の相似の関係と組み合わせるパターンです。

次図はその１つの例で、隠れてる扇形を見つける必要がある事、三平方の定理か三角比を使って１つの辺の長さを出す必要がある事から、一手間かかるタイプの問いです。

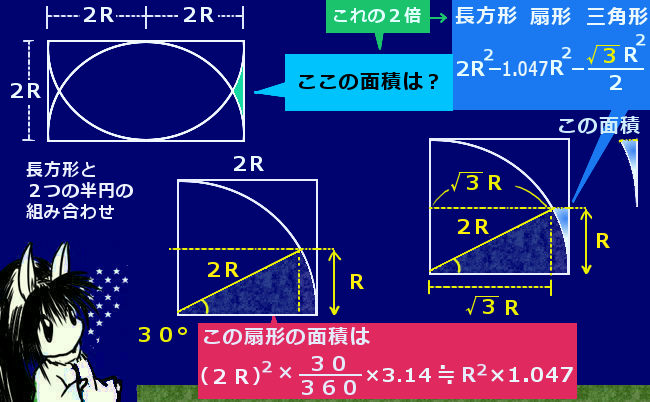
高校数学の場合はこのような問いが出題される頻度は少なくなりますが、積分の問題として、似たような図形の面積を計算させる問いは出題されます。