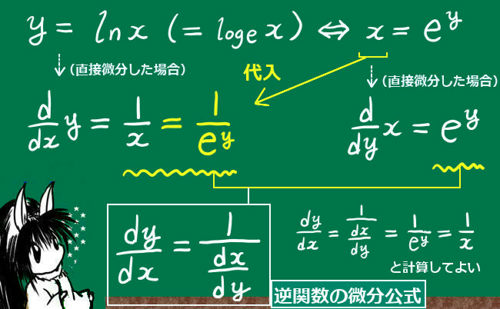
逆関数の微分公式の内容、具体例、証明について述べます。
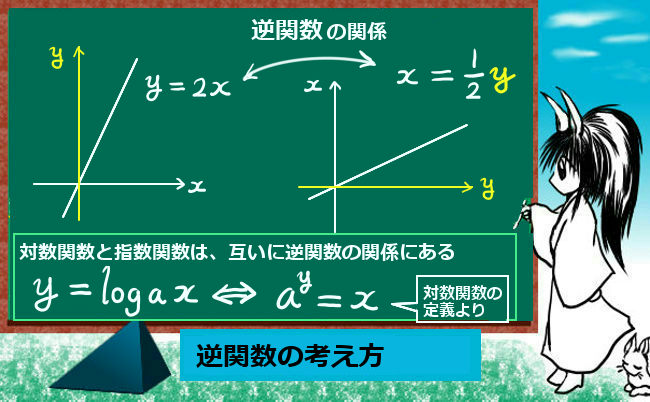
y = 2x のとき、両辺を2で割って x = y / 2 とも書けます。
このように、y = y(x) のとき、逆に x = x(y) と書けるとき、x(y) を y(x) の逆関数と呼びます。
【この時の関数の記号はfでもFでも何であっても問題ありません。】
高校数学の中で重要な例としては、指数関数と対数関数を挙げる事ができます。
これらは、互いに逆関数同士の関係にあるのです。
y=x2 のような場合に逆関数を考えると x=\(\pm \sqrt{y}\)のように x を y で表した関数が2つ出てきてしまうので、「1つの変数に対して1つの値が定まる」という関数の定義に反し、ちょっとした面倒事が起きます。
こういう場合には x の定義域と y の値域を特定の区間に定めれば逆関数を書けるという形になります。
逆関数の定義に関するそういった細かい事は多くあるのですが、ここでは本質ではないので略します。
高校数学で覚える必要はありませんが三角関数の逆関数を「逆三角関数」と言い、
sin x に対して arcsin x(「アークサイン x」)と書きます。
この逆三角関数は一見使いづらい関数なのですが、
その微分の性質から、一部の微積分の計算(例えばテイラー展開や不定積分の計算)で有用な働きをする事があります。この逆三角関数を微分する時には、逆関数の微分公式を使用します。
公式の内容
逆関数を考えた時、もとの関数を微分して得られる導関数と、逆関数を微分して得られる導関数の間にはある関係式が必ず成立するというのが、逆関数の微分公式です。内容は、次のようになります。
y=y(x)の時にx=x(y)と表せる時、次の関係式が成立します。
$$\frac{dy}{dx}={\large\frac{1}{\frac{dx}{dy}}}$$
ここで左辺はxの関数で、具体的な計算においては右辺はyの関数ですが、yはxで表せるという前提なので右辺もxだけの関数として表す事ができます。(※ただし後述するように具体的な計算ではyをxに直す作業が面倒である事があります。)
もちろん、分母は0になってはいけないという前提はあります。
ちょっと一見よく分からない公式だと思うかもしれませんが、xをyで表した時に「xをyで微分して得られる導関数」の逆数が、もとのyをxで微分して得られる導関数に必ず等しくなるという関係式です。
式としては単純で互いに逆数であるという関係ですから、dx/dy=・・の形として見ても公式は成立します。つまり基本的には公式を次のように書き換える事もできます。
$$\frac{dx}{dy}={\large\frac{1}{\frac{dy}{dx}}}$$
これは、具体例で見たほうが分かりやすいと思います。
具体例と計算例
具体的に公式を使うための手順は次のようになります。
もとの関数y=y(x)の導関数を計算したい場合であるとします。
- 関数と逆関数を、y=y(x), x=x(y) の形で出しておく。
- 逆関数のほうについて、導関数を計算する。【※これが簡単にできる場合でないと、公式を使う意味があまりない事になります。】$$\frac{dx}{dy}を計算$$
- 得られた逆関数の導関数(yの関数)を、逆関数の微分公式に代入します。$$\frac{dy}{dx}={\large \frac{1}{\frac{dx}{dy}}}\hspace{5pt}に\hspace{5pt}\frac{dx}{dy}\hspace{5pt}を入れる$$
- この段階で得られる計算結果は「y の関数」の形になっているので、y=y(x)を代入して x の関数にすれば、
それが y に対して x で微分したdy/dxの正しい形になっています。 $$式の変数をxだけにすれば\hspace{5pt}\frac{dy}{dx}\hspace{5pt}の結果になる$$
※合成関数でもこの「y を x の関数の形に戻す」作業がありますが、一般には y = f(x) を代入すればよいというものでした。しかし、逆関数の微分の場合は、この作業について少し工夫がいる場合があります。
具体的な計算例を次に記します。
ここでは参考までに、逆三角関数の微分の計算も記してあります【高校では不要】。
逆関数の微分公式は、通常の微分計算で多く使うというよりは、特定の微分公式を導出するために使われる事が多いように思います。
- 1次関数の例:y=2, x=y/2 の時、 $$\frac{dx}{dy}=\frac{1}{2}\hspace{5pt}により、$$ $$\frac{dy}{dx}={\large\frac{1}{\frac{dx}{dy}}}={\large\frac{1}{\frac{1}{2}}}=2$$ この場合には直接微分しても、あるいはグラフを見ても分かる結果ではありますが、逆関数の微分公式も確かに成立しているという事です。
- 2次関数の例:x>0かつ y=\(\sqrt{x}\), x=y2 の時、
$$\frac{dx}{dy}=2y\hspace{5pt}により、$$
$$\frac{dy}{dx}={\large\frac{1}{\frac{dx}{dy}}}=
\frac{1}{2y}
=\frac{1}{2\sqrt{x}}$$
ここでは平方根のほうの導関数を計算するために、2次関数を逆関数とみなしています。
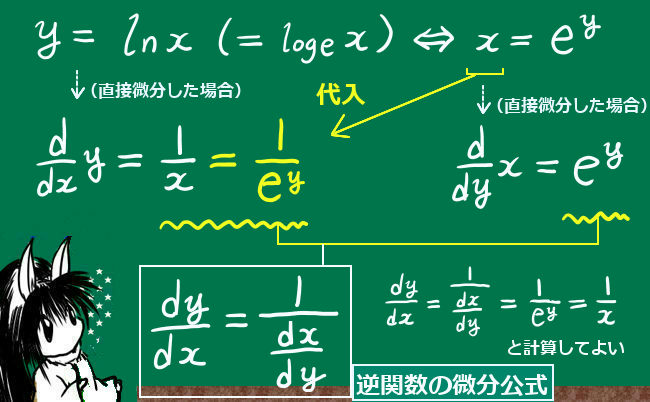
もちろん、この計算はyを直接xで微分しても同じ結果です。 - 指数関数と対数関数の例:y=ex, x=ln y の時、 $$\frac{d}{dx}e^x={\large\frac{1}{\frac{d}{dy}\ln y}}={\large\frac{1}{\frac{1}{y}}}=y=e^x$$ 指数関数と対数関数の微分公式は一見全く異なる形であるようにも見えますが、じつはこうしたつながりもあるというわけです。
- 逆三角関数と三角関数の例:y= arcsin x, x= sin y の時、$$\frac{d}{dx}\arcsin x={\large\frac{1}{\frac{d}{dy}\sin y}}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-\sin^2y}}=\frac{1}{\sqrt{1-x^2}}$$
ここでは「逆三角関数の導関数」を知るために、通常の三角関数を逆関数とみなしています。
計算過程では sin2x+cos2x=1 の関係を使用しています。 - 余弦の逆三角関数の例:y=arccos x, x=cos y の時、$$\frac{d}{dx}\arccos x={\large\frac{1}{\frac{d}{dy}\cos y}}=\frac{1}{-\sin y}=\frac{-1}{\sqrt{1-\cos^2y}}=\frac{-1}{\sqrt{1-x^2}}$$
- 正接の逆三角関数の例:y=arctan x, x=tan y の時、 $$\frac{d}{dy}\tan y==\frac{1}{\LARGE{\frac{1}{\cos^2y}}}\hspace{5pt}により、$$ $$\frac{d}{dx}\arctan x={\large\frac{1}{\frac{d}{dy}\tan y}}=\cos^2y=\frac{1}{1+\tan^2y}=\frac{1}{1+x^2}$$
高校数学では、指数関数と対数関数の関係あたりを逆関数の関係で結べる事を理解していれば、基本的にはじゅうぶんかと思います。
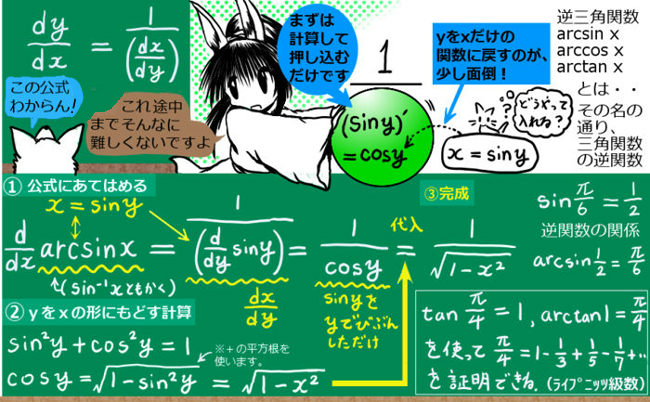
ただ、そのあとで y を x の関数の形にうまく戻すために、工夫が必要な事があるのです。
※逆三角関数の別の表記方法
あくまで表記方法の問題なのですが、逆三角関数を sin-1xとも書きます。
もちろんその場合は(sin x)-1=1/(sin x) とは全く異なる関数・・なのです。
個人的にこれは紛らわしい表記だとも思うので、このサイトでは arcsin x などの表記を使用します。
公式の証明
y=Y(x), x=X(y) として、まず Δx = X(y+k)-X(y) とすると
k → 0 の時に Δx → 0 となります。(その逆である「Δx→ 0 の時 k → 0 」も成立)
X(y+k)-X(y) について Δx という文字でおいたのは、ここでは X(y+k)-X(y) というものが「xの変化」に等しいという事を見やすくするためです。別に他の文字でも支障はありません。
これを上手に利用すると、同じ極限が2通りの方法で表せます。その2通りの方法による結果がdy/dxと1/(dx/dy)であり、それゆえに両者を等号で結べるというのが証明の内容です。
その点で、合成関数の微分公式のように1本の式だけで証明できない点が少しだけ異なります。
ここで、微分の定義の式を書きます。
$$\frac{dy}{dx}={\large\lim_{\Delta x \to 0}\frac{Y(x+\Delta x)-Y(x)}{\Delta x}}$$
これは定義通りの式です。しかし、極限をとる変数としてΔxを使っているところに計算上の工夫があります。ここの極限をとる変数は、h でなくとも何でも成立します。
上記の微分を表す微分を計算すると、次のようにも表せます。
$$ {\large\lim_{\Delta x \to 0}\frac{Y(x+\Delta x)-Y(x)}{\Delta x} } =\lim_{k \to 0}{\large\frac{Y(X(y)+X(y+k)-X(y))-Y(X(y))}{\Delta x}}$$
$$ ={\large\lim_{k \to 0}\frac{Y(X(y+k))-Y(X(y))} {\Delta x}} ={\large\lim_{k \to 0}{\large\frac{y+k-y}{\Delta x} }} ={\large\lim_{k \to 0}\frac{k}{\Delta x} }={\large\lim_{k \to 0}\frac{1}{\frac{\Delta x}{k}} }$$
$$ ={\large\lim_{k \to 0}\frac{1}{\frac{X(y+k)-X(y)}{k}} } ={\Large\frac{1} {\frac{dX(y)}{dy}}}={\Large\frac{1}{\frac{dx}{dy}} }$$
最初の変形では、分子のところだけΔxをもとの形Δx = X(y+k)-X(y)に直してしまい、
xをx=X(y)で書く事により、x+Δx=X(y+k)としています。
次に、関数を y 変数になるように整理し、Δx→0 の時 k→0 なので k の極限にしています。
そのあとで、少しややこしいのですが逆関数の重要な性質「Y(X(y))=Y(x)=y 」(X(y)=xに注意)を使って、X(Y(y+k)) = y + k としています。
その後の計算は、例えば2/3=1÷(3/2)=1/(3/2)などと、同じ計算です。
これらの結果から、
$$\lim_{\Delta x \to 0}{\large\frac{Y(x+\Delta x)-Y(x)}{\Delta x}}=\frac{dy}{dx}={\Large\frac{1}{\frac{dx}{dy}} }【証明終り】$$