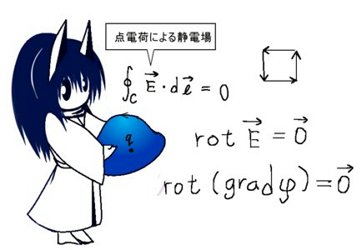
静止した電荷あるいは電荷の分布が作る静電場(時間による値の変動がない電場)についてはクーロンの法則と、その一般的な形であるガウスの法則が成立します。そしてもう一つ、「渦無しの法則」というものも成立します。
渦無しの法則とは
ここで言う電場の「渦」というのは数式としては流体力学等で想定されるものと同じ形の式です。すなわち、数式的にはベクトル場の「回転」(「カール」「ローテーション」とも)によって表す量です。
静電場を構成するものが静電荷あるいはその分布であるときには、電場が定義される任意の位置において電場の回転\(\mathrm{rot}\overrightarrow{E}\)はゼロベクトルになる事が数式的に証明できます。それが静電場の渦無しの法則と呼ばれるものです。
また、それと同時に循環と呼ばれる量も0になる事が示されて、それを静電場の渦無しの法則と呼ぶ事もあります。この循環という量は、数式的にはベクトル場の閉曲線に対する接線線積分です。2つの事実関係はストークスの定理によって結び付けられるので、どちらの事を渦無しの法則と呼んでも同じ事になります。
静止した電荷(またはその分布)がある時、
それによる電場が定義できる任意の位置で次式が成立します。
$$\mathrm{rot}\overrightarrow{E}=0$$
ナブラ記号を使って書けば次のようになります。
$$\nabla×\overrightarrow{E}=0$$
また、同じく静止した電荷が作る電場の循環(circulation)について
電場が定義される範囲で任意の閉曲線Cに対して次式が成立します。$$\oint_C\overrightarrow{E}\cdot d\overrightarrow{l}=0$$
実は電場の循環は、閉曲線Cに沿って単位電荷が1周分する時の「電場が行った仕事」です。渦無しの法則は、静電荷が作る静電場においてはそれが任意の閉曲線で0になる事を言っています。その事は電磁誘導によって回路等に起電力と誘導電場が生じる時には渦無しの法則が成立しない事との関係が大いにあります。
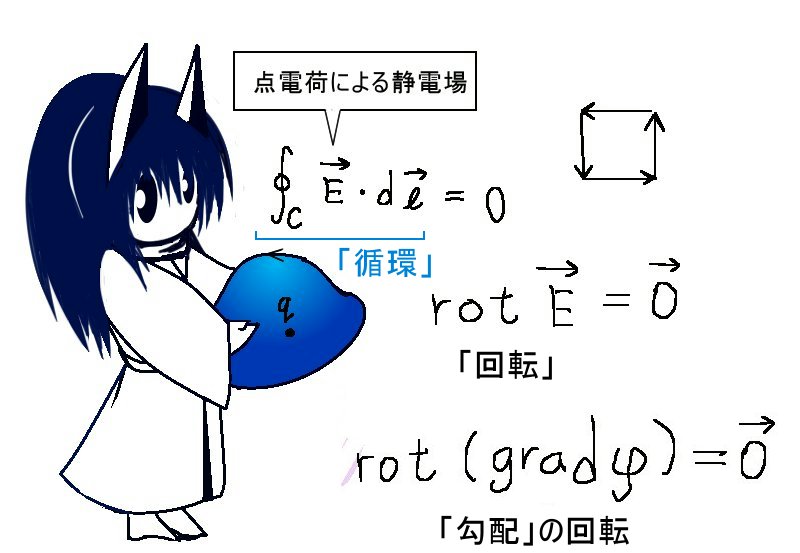
また、後述する事に関係しますが定電流によって作られる静磁場の場合には回転も循環も0にはなりません。つまり点電荷による静電場では渦無しの法則が成立し、逆に定電流による静磁場では渦無しの法則は成立せず「渦」がある状態になります。
渦無しの法則における回転と循環の関係
渦無しの法則における回転と循環の関係について先に示しておきましょう。
ストークスの定理により次式が成立します。
$$\oint_C\overrightarrow{E}\cdot d\overrightarrow{l}=\int_S\mathrm{rot}\overrightarrow{E}\cdot d\overrightarrow{s}$$
ここで、まず回転に関して渦無しの法則が成立するならストークスの定理の右辺(法線面積分の項)は0ですから、左辺の循環もそのまま0になるわけです。
$$\mathrm{rot}\overrightarrow{E}=0であるとき\oint_C\overrightarrow{E}\cdot d\overrightarrow{l}=\int_S\mathrm{rot}\overrightarrow{E}\cdot d\overrightarrow{s}=0$$
次に循環に関して渦無しの法則が成立する時にはストークスの定理の右辺が0という事になりますが、これは法線面積分が0という事であって積分対象の\(\mathrm{rot}\overrightarrow{E}\)が0という事を直ちには示しません。しかし、渦無しの法則が意味するところは閉曲線Cが特定のものではなく「任意」であるという事なので、積分対象の関数が高等的に0である事を意味します。
$$\oint_C\overrightarrow{E}\cdot d\overrightarrow{l}=0の時には\oint_C\overrightarrow{E}\cdot d\overrightarrow{l}=\int_S\mathrm{rot}\overrightarrow{E}\cdot d\overrightarrow{s}=0$$
$$この式は「任意の」閉曲線Cで成立するので\mathrm{rot}\overrightarrow{E}=0$$
(ストークスの定理における曲面Sは、閉曲線Cを外縁に持つ任意の開曲線。)
この論法はガウスの発散定理を使って静磁場の発散について積分形から微分形を導出する時のやり方に似ています。
これにより、点電荷が作る静電場の回転が0である事と、循環が0である事のどちらを指して渦無しの法則と呼んでも数式的には同じであると言えるわけです。
静電場の回転の直接計算による導出
静止した点電荷が作る電場について渦無しの法則が成立すれば電荷が複数あってもベクトル場は重ね合わせ(ベクトルの和)で計算されるので同じく渦無しの法則が成立する事になります。
考え方や導出・証明方法はたくさんあるのですが、実は電場の回転を定義に従って普通に計算しても意外に簡単に結果が出ます。そこで、まず偏微分の直接計算によって回転が0になる事を示し、次にそれが「偶然なのか必然だったのか」について考察してみましょう。
点電荷の電気量をQ【C】、比例定数はまとめてkとして、座標を使った電場ベクトルを成分で書きます。見やすくするようにkで割ったものを考えると次のようになります。
$$\frac{1}{k}\overrightarrow{E}=\left(\frac{x}{(x^2+y^2+z^2)^{\frac{3}{2}}},\frac{y}{(x^2+y^2+z^2)^{\frac{3}{2}}},\frac{z}{(x^2+y^2+z^2)^{\frac{3}{2}}}\right)$$
他方、電場の回転\(\mathrm{rot}\overrightarrow{E}\)は次のようなベクトルです。
$$\mathrm{rot}\overrightarrow{E}=\left( \frac{\partial E_3}{\partial y}-\frac{\partial E_2}{\partial z} ,\hspace{5pt} \frac{\partial E_1}{\partial z}-\frac{\partial E_3}{\partial x} ,\hspace{5pt} \frac{\partial E_2}{\partial x}-\frac{\partial E_1}{\partial y} \right)$$
一見計算するにならないかもしれませんが、商の微分公式と合成関数の微分公式を使って回転の第3成分を計算してみると次のようになります。上記と同じく比例定数kで割った状態で計算します。
$$\frac{1}{k}\mathrm{rot}\overrightarrow{E}の第3成分\frac{\partial E_2}{\partial x}-\frac{\partial E_1}{\partial y}$$
$$=\frac{-2x\cdot\frac{3}{2}\cdot(x^2+y^2+z^2)^{\frac{1}{2} } y}{(x^2+y^2+z^2)^3}+\frac{2y\cdot\frac{3}{2}\cdot(x^2+y^2+z^2)^{\frac{1}{2} } x}{(x^2+y^2+z^2)^3}$$
$$=\frac{-3xy}{(x^2+y^2+z^2)^{\frac{5}{2}}}+\frac{3xy}{(x^2+y^2+z^2)^{\frac{5}{2}}}=0$$
このように、意外にそこまで複雑というわけでもなく第3成分は0になると言う結果を得ます。
全く同じように計算すると第1成分と第2成分も0になるので、渦無しの法則の式 \(\mathrm{rot}\overrightarrow{E}=0\) が導出されます。
勾配と回転の関係からの導出
さて「計算したら上手い具合に0になった」というのは偶然でしょうか?
実の所、「ある程度は必然の結果であった」と言えるのです。これは、スカラー場の勾配ベクトルに対する回転は必ず0(ゼロベクトル)になるという公式が存在するためです。
勾配が定義できるスカラー場について、
3変数のそれぞれで2階までの連続な偏導関数が存在する時には次式が成立します。$$\mathrm{rot}(\mathrm{grad}\phi)=0$$
この公式の証明は直接計算でできます。これも、意外と複雑ではないのです。
$$\mathrm{grad}\phi=\left(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y},\frac{\partial \phi}{\partial z}\right)なので$$
$$\mathrm{rot}(\mathrm{grad}\phi)= \left( \frac{\partial^2 \phi}{\partial y\partial z}- \frac{\partial^2 \phi}{\partial z\partial y} , \frac{\partial^2 \phi}{\partial z\partial x}- \frac{\partial^2 \phi}{\partial x\partial z} , \frac{\partial^2 \phi}{\partial x\partial y}- \frac{\partial^2 \phi}{\partial y\partial x} \right)$$
$$= \left( \frac{\partial^2 \phi}{\partial y\partial z}- \frac{\partial^2 \phi}{\partial y\partial z} , \frac{\partial^2 \phi}{\partial z\partial x}- \frac{\partial^2 \phi}{\partial z\partial x} , \frac{\partial^2 \phi}{\partial x\partial y}- \frac{\partial^2 \phi}{\partial x\partial y} \right)=(0,0,0)$$
つまり、回転ベクトルの成分の構成が規則的である事と、偏微分を複数回行う時には順序によらず同じ結果となるという条件のもとで公式が成立するわけです。
偏微分の順序については「なめらかな関数」に対しては普通はあまり気にしないでよいのですが、特定の点や領域で微分可能性が怪しくなる場合には注意が必要な事があります。
複数の変数での偏微分において順序によらず同じ偏導関数が得られる保証があるのは
「偏微分を行う階数Nに対していずれの変数でもN階以下の連続な偏導関数が全て存在する事」になります。
このNは、例えばxとyで1回ずつ偏微分する場合には「2回」と数えます。
さて、公式 rot(gradφ)=0の意味を考えてみると、
あるベクトル場が「何らかのスカラー場の勾配ベクトルになっていて偏微分に関する条件も満たす」のであれば回転ベクトルは0になるという事になります。さらに言い換えると、そのようなスカラー場が存在するならば\(\mathrm{rot}\overrightarrow{F}=0\) が成立すると言えるのです。
静電場の渦無しの法則に戻ると、点電荷が作る電場に対してはそのようなスカラー場が存在する事ができて、それがいわゆる「電位」です。静電場においては電位は「単位電気量(1[C])の電荷の位置エネルギー」であるという意味付けができます。(2地点の電位の差である「電位差」がいわゆる「電圧」です。)
静電場から電位を計算する時には接線線積分を考えますが、無限遠を基準にとれば点電荷からの距離を変数とする変数の定積分として計算ができます。その結果として得られるスカラー場の勾配ベクトルを考えると、それはもとの静電場に戻るのです。ですので、実は成分の直接計算をしなくても、点電荷が作る静電場には電位が存在する事から渦無しの法則も成立すると言う事もできるのです。
$$\mathrm{grad}V=\overrightarrow{E}となる電位Vが存在し、これは所定の条件を満たすので\mathrm{rot}\overrightarrow{E}=0$$
また、静止した点電荷に対する電位を具体的に計算すると点電荷からの距離r【m】に反比例する形になりますので、その関数は点電荷自身の位置を除けば任意の点で何回でも偏微分可能ですから先ほど少し触れた「偏微分の順序」についても気にしなくてよい事になります。
電磁場で「渦」がある場合
逆に渦無しの法則が成立しない状況は電磁場においてどのようなものがあるかというと、ここでは簡単にだけまとめておくと代表的なものとして次のようなものがあります。
まず磁場の時間変動がある場合には電場にの回転はゼロではなくなります。これが電磁誘導の法則の内容であり、起電力が生じる事を意味しています。
次に、定電流が作る静磁場についても電流が生じている導線まわりの閉曲線においてはアンペールの法則により接線線積分の値はゼロにならず、渦ができていると考えられます。(ただし、この時の回転ベクトルと接線線積分に関する数学的な扱いには少し注意する必要もあります。)この場合には、アンペールの法則の意味としては電流もそうですが電場の時間変化(変位電流)にも起因して磁場の回転が発生する事を意味します。その事を指して起磁力と言う言葉が使われる事もあります。(起電力に対応する語)。
つまりごく簡単に言うと電場の時間変動(あるいは電流)によって磁場が作られて、磁場の時間変動によって電場(あるいは電流)が作られる関係があります。そしてその時に、循環の形の接線線積分で表される「渦」が生じるという体系になっていると言えます。
また電流の種類で「渦電流」というものも存在しますが、それはまた別の扱いが必要になってきます。