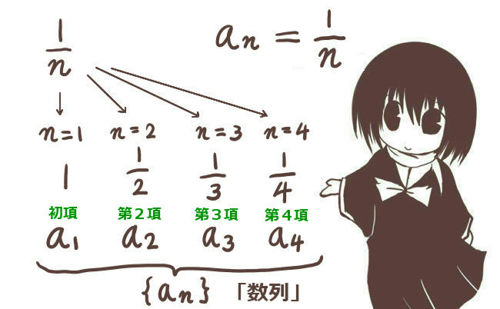
数列(「すうれつ」)とは、自然数や整数を代入する事で決定する種類の関数の事です。
考え方:関数と数列
普通の関数y=x2などを考えて、変数の値を自然数に限定しy=n2と考えると、
n=1,2,3,4,・・に対してy=1,4,9,16,・・と決定していきます。これが数列の例です。
要するに考え方は1次関数や2次関数などの普通の関数と同じで、変数を自然数や整数に限定したものを特に「数列」と呼びます。
この時に番号nに対して決まる関数の値(数列の値)のことを、
てきとうな文字と番号を組み合わせてynのように書きます。これはy=f(x)と書くのと同じような使い方です。添えてある番号を式に代入しますよ、という意味です。
例えばy=n2を数列と考えてy2と書いたときには
「y=n2においてn=2とした場合」の事を意味し、y2=22=4のようになります。
一般の関数と区別して「数列」である事を明示するために数列を{yn}のようにも表記します。文章の中での表記のされ方としては「自然数nに対して数列{yn}があり、yn=n2である」といった具合です。
一般的には、数列を表す文字はa、b、c・・を使ったan、bn、cnなどを優先して使う事が多いですが、本質的には番号を下に添えてあればどんな文字でも数列として表記できます。
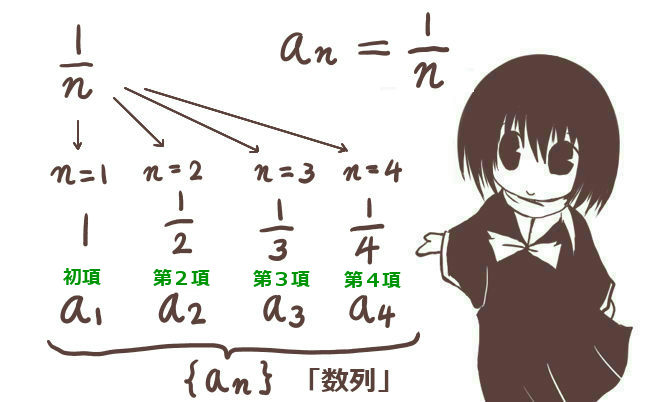
数列{an}があったときに、一番最初の値を「初項」(しょこう)と言います。
nが自然数であれば、a1が初項として該当します。an=1/nであれば、初項はa1=1/1=1です。2番目の値は「第2項」のように言います。この時、ものによっては番号を0から始める場合もあり、その時には初項はa0です。あくまで、一番最初の項を初項と呼ぶという事です。
漸化式と初歩的な数列
数列を扱う時の一般の関数との違いは、「漸化式」(ぜんかしき)というものを考える事が多いという点です。これは、an+1=2+anのように、n+1番目とn番目などの数列の項の間に成立する関係式を指します。
★「漸」(ぜん)とは、「次第に進む」とか「徐々に進む」といった意味の漢字です。
この場合、例えばa3=2+a2で、
さらにa2=2+a1なのでa3=2+a2=2+(2+a1)=4+a1のようにもなります。
an+1=2+anのような関係であれば、an=2+an-1としてもよいという事です。この考え方は漸化式を扱ううえで重要です。(番号が1から始まっているような場合には、この漸化式an=2+an-1を適用できるのはa2までであり、a1には適用不可です。)
より一般的には漸化式とは数列の項同士のかなり広い関係全般を差します。
例えばan+1=an3とか、複数の項を考えたan+3=an+2+an+1+anなども漸化式です。
「n+1とn」のように数列の異なる2項についての漸化式を特に言う場合は「2項間漸化式」、「n+2とn+1とn」のように異なる3項についての漸化式を特に言う場合は「3項間漸化式」と言う事もあります。より一般的には「m項間漸化式」も考えれるという事です。
番号が1つではなく2つ飛んでいる場合もあり得ます。例えばan+2=2+anなどです。
このようにあらゆるものが当てはまりますが、普通は漸化式の関係から具体的な数列の形を導出したり、あるいは和や極限を計算するために漸化式を使うので、実際問題として理論で扱われる漸化式はある程度の扱いやすい規則性を持つものに限られます。
高校数学では、特に3つの初歩的な数列を扱います。これらは意味としては簡単なものですが、いずれも漸化式によって特徴付けられます。
- 等差数列
an+1=c+an で表されます。
cは定数で、「公差」(こうさ)と言います。
an=a1+c(n-1) とも直接的に表せます。 - 等比数列
an+1=anr で表され ます。
rは定数で、「公比」(こうひ)と言います。
an=a1rn-1 とも直接的に表せます。 - 階差数列
bn=an-an-1 で表されます。
an-an-1を数列{an}の「階差」(かいさ)と言います。
bn=an-an-1は「{an}の階差数列」であるとも言います。

等差数列とは、1つの項に決まった定数を加える(あるいは減じる)事で次の項が確定するというタイプの数列です。例えばan+1=3+anを考え、a1=2とします。この時、a2=3+a1=3+2=5、a3=3+a2=3+5=8、a4=3+a3=3+8=11、・・・のように次々と計算できます。
これを繰り返して一般的に、an=3+2(n-1)とも表せます。例えばa4=3+2(4-1)=11と計算してもいいわけです。
等比数列とは、1つの項に決まった定数を掛ける(あるいは割る)事で次の項が確定するというタイプの数列です。例えばan+1=3anでa1=2であるとき、a2=3a1=3×2=6、a3=3a2=3×6=18、a4=3×a3=54、・・・といった感じです。これを繰り返して、an=a13n-1とも書けます。
等比数列に関しては、和を計算する公式が重要です。
階差数列とは、上記の通りbn=an-an-1といった形の漸化式で表される数列です。これの具体的な形は、階差数列の和を考えてみる事で計算できるという特徴があります。
特定の{an}について階差数列bnを考える時には例えば次のようにします。an=n2のとき、「階差」を計算するとn2-(n-1)2=2n-1なのでbn=2n-1と書けます。
この時、nが整数ならこの形で整合性がとれますが、もし{an}のnが自然数といった制限を課しているならb1については別途に「b1=-1とする」などとする必要があります。
いろいろな数列
関数には様々なものが想定できるのと同じように、数列も非常に幅広いものを指します。
例えば、数列{an}の和を考えてa1+a2+a3+・・・+an=Snとして、
それ自体を数列{Sn}と考える事ができます。
尚、この時Snー1=a1+a2+a3+・・・+an-1ですから、{Sn}の階差はSn-Snー1=anです。この関係自体は、当然といえば当然のものですが結構よく使います。
微積分学で重要な「自然対数の底」eは、ある数列を考えて、そのn→∞における極限値として定義されます。そのように、数列は極限と合わせて考えられる事も多いのです。
$$e=\lim_{n\to\infty}\left(1+\frac{1}{n}\right)^n\hspace{10pt}として定義されます。$$
また、極限値として円周率が存在する事を式で証明する時にも、図形上の辺の関係を漸化式で表しています。この場合に考えるのは、正n角形と正2n角形を考えてa2nとanの関係を出すという、少し特殊な漸化式です。
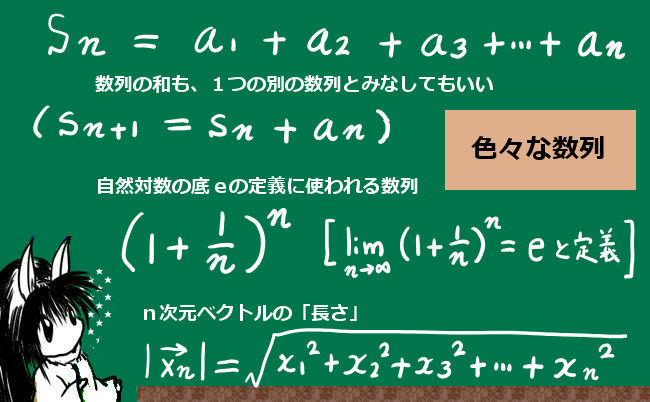
その他に、高校ではあまり扱いませんが「関数列」というものもあります。
これは、nによって関数自体の形が決まる数列{fn(x)}を考えるという意味です。1つ1つのfn(x)は定義域内のxによる関数であるという事です。
例を考えると意味としては難しくなくて、例えばfn(x)=xnやgn(x)=sin(nx)などを数列として考える場合には関数列であるということになります。
数列として見る場合、x,x2,x3,・・,xnのようにn個の関数があると見るわけです。
ベクトルなどでも、n次元に対してn+1次元を考えるというふうにすると諸量を数列的に見る事もできます。そのようにすると、何かの証明を行う際に数列的な計算が使えるので利点があったりします。