数列などについて成立する和の公式についてまとめました。
nの1乗、2乗、3乗に関する和
1+2+3+4+5+6+7=28です。
これは直接足し算をしてもよいのですが、じつは7×8÷2=28のようにも計算できます。
これは偶然ではなくて必然であるというのが、数列の和に関する公式です。
1から100までの自然数の和も、100×101÷2=5050のように計算できます。
同様に1からnまでの自然数の「2乗」や「3乗」を全て加えた時に成立する公式があります。
- 1~nまでの自然数の和 $$\sum_{j=1}^nj=\frac{n(n+1)}{2}$$
- 1~nまでの自然数のそれぞれの「2乗」の和 $$\sum_{j=1}^nj^2=\frac{n(n+1)(2n+1)}{6}$$
- 1~nまでの自然数のそれぞれの「3乗」の和$$\sum_{j=1}^nj^3=\frac{n^2(n+1)^2}{4}$$
4乗の和以降の公式も理論的には作れますが、複雑になるので公式として使われる事は基本的にはありません。Σ(シグマ)は和を表す記号です。
これらのうち、特に1+2+3+・・+nを表す公式は何かの個数の数え上げの際に(突然)使う時があるので、知っておくと便利な公式です。
ここで、もし1から「n-1」まで加えるといった場合には、単純に上記公式でnのところをn-1に置き換えれば計算可能です。例えば1~n-1までの和は次のようになります。
$$\sum_{j=1}^{n-1}j=\frac{n(n-1)}{2}$$
n→n-1と、n+1→(n-1)+1=n の置き換えで、
結果的にn(n-1)のように書けるという事です。
証明については高校で「証明せよ」という形で問われる事はほとんどないと思いますが、一応どういう根拠であるのかを知っておき、また計算問題の練習としてやってみるのもよいと思います。
図を使う方法も含めて複数の証明方法がありますが、例えば次のように考えます。
1+2+3+4+・・・+n-1+n=Sとした時、
全く同じ式を「和の順番だけ入れ替えた」ものを考えます。
つまり、n+(n-1)+(n-2)+(n-3)+(n-4)+・・・+2+1=Sを考えます。
2つ並べて、左辺と右辺をそれぞれについて加えます。
1+2+3+4+・・・+n-1+n=S
n+(n-1)+(n-2)+(n-3)+(n-4)+・・・+2+1=S
この時、左辺については左から見て何番目の項であるかを合わせて加えます。
例えば、左から3番目にある項は3とn-2なのでこれらを足し合わせる形にします。
すると、次のようになります。
(1+n)+(1+n)+(1+n)+・・・+(1+n)=2s
(1+n)という項はn個ある事に注意すると、
n×(1+n)=2S ⇔ S=n(n+1)/2となり、和の公式を得ます。
ここでどの項も必ず(1+n)になるという事は、
左からm番目の項についてm+(n-m+1)=n+1となるので保証されるというわけです。
【例えばn=3なら3+(n-3+1)=3+(nー2)=n+1です。】

では、2乗の和についてはどうでしょう。考え方は似ているのですが、少し工夫が必要です。
まず、1+2+3+・・・+nを考えます。
この時、最初から2乗を考えずに1乗を考えるところがポイントです。
これについては公式が得られているので1+2+3+・・・+n=n(1+n)/2
続いて、2+3+・・+nを考えます。
これは全体から1を引いただけなので2+3+・・+n=n(1+n)/2-1です。
さらに、3+4+5+・・・+nなどを考えていきます。
1+2+3+4+5+・・・+n=n(1+n)/2
2+3+4+5+・・・+n=n(1+n)/2-1
3+4+5+・・・+n=n(1+n)/2-1-2
4+5+・・・+n=n(1+n)/2-1-2-3
5+・・・+n=n(1+n)/2-1-2-3-4
・・・
n=n(1+n)/2-1-2-3-4-・・・-(n-1)
を考えます。
これらn個の式の両辺を全部加えて等号でつなぐと、
左辺については1が1個、2が2個、3が3個、4が4個、・・・nがn個ある事が分かります。
3が3個という事は3×3=32ですから、これで「2乗」の和ができるわけです。
右辺については、まずn(1+n)/2がn個ですからn2(1+n)/2という項があります。(これが公式で「nの3乗」がある理由です。)
続いて引き算の部分は、1乗の和で表されるものをさらに1~n-1について和をとる事になります。
1~n-1までの和としてΣ{j(1+j)/2}を考えるという事です。
この時に「2乗の和」が発生しますが、これは左辺にもありますので移項できます。
ただし、右辺で生じるのは「1からn-1までの」2乗の和なので、「1からnまでの2乗の和」からn2を引いたものになります。
12+22+32+42+・・・+n2=Sとして、
$$S=n\cdot\frac{n(n+1)}{2}-\sum_{j=1}^{n-1}\frac{j(j+1)}{2}=\frac{n^2(n+1)}{2}-\frac{(S-n^2)}{2}-\frac{n(n-1)}{4}$$
⇔3S/2=n2(n+1)/2+n2/2-n(n-1)/4
=(2n3+3n2+n)/4
=n(n+1)(2n+1)/4 【うまい具合に因数分解できます。】
⇔S=n(n+1)(2n+1)/6

3乗の和の公式も同じようにできて、今度は2乗の和から1つずつ項を引いたn個の式を加えます。
1+22+32+42+52+・・・+n2=n(n+1)(2n+1)/6
22+32+42+52+・・・+n2=n(n+1)(2n+1)/6-1
32+42+52+・・・+n2=n(n+1)(2n+1)/6-1-22
42+52+・・・+n2=n(n+1)(2n+1)/6-1-22-32
52+・・・+n2=n(n+1)(2n+1)/6-1-22-32-42
・・・
n=n(n+1)(2n+1)/6-1-22-32-42-・・・-(n-1)2
32が3個あれば3×32=33、m2がm個あればm×m2=m3ですから、
左辺の合計は3乗の和になります。
右辺は、n(n+1)(2n+1)/6がn個と、「2乗の和」の形の数列をさらに1~n-1まで和をとったものを引いたものになります。j(j+1)(2j+1)/6=(2j3+3j2+1)/6なので、これについて1~n-1まで和をとり、引き算するという事です。
少し長ったらしいですが式を整理すると次のようになります。
1+23+33+43+・・・+n3=Sとして、
$$S=\frac{n^2(n+1)(2n+1)}{6}-\frac{S-n^3}{3}-\frac{n(n-1)(2n-1)}{12}-\frac{n(n-1)}{12}$$
$$\Leftrightarrow \frac{4S}{3}=\frac{4n^4+8n^3+4n^2}{12}=\frac{n^2(n+1)^2}{3}$$
$$\Leftrightarrow S=\frac{n^2(n+1)^2}{4}$$

等比数列の和
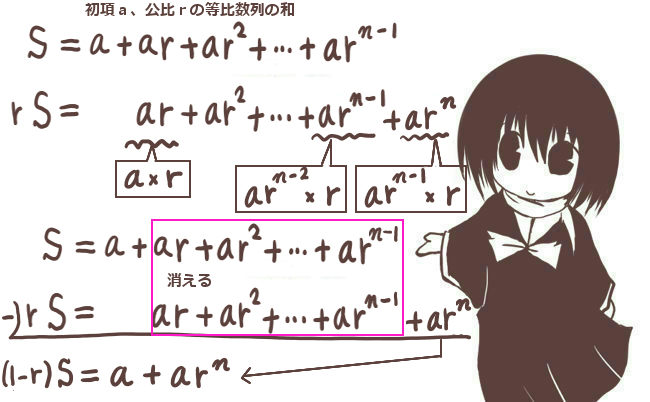
何かと重要になるのは「等比数列の和」です。これは次のようにします。
S=a+ar+ar2+ar3+・・・+arn-1
これの両辺にrを掛けます。
rS=ar+ar2+ar3+・・・+arn-1+arn
SとrSは、項数は同じで、途中のar+ar2+ar3+・・・+arn-1が共通しています。
共通する項は差し引けばもちろん0になるので、
S-rS=a+arn ⇔ S(1-r)=a+arn
r=1の時は単にn個のaの和なのでS=naで、r≠1のときはS=(a+arn)/(1-r)です。
これは、r=1/2のときなど、n→∞のときにrn→0となる場合が特に重要です。そのように項数を無限個にした場合の等比数列の和は、等比級数あるいは幾何級数と言います。
階差数列の和
bn+1=an+1-anのような形の数列(「階差数列」)の和を考えるとき、
bn+2=an+2-an+1のようになりますから、
bn+2+bn+1=an+2-anになります。
中間の項がプラスマイナスでちょうど消えるという事です。
さらにbn+3=an+3-an+2を加えれば、
an+2が消えてbn+3+bn+2+bn+1=an+3-anになります。
このような形で、階差数列の和を計算する事ができます。具体的に書きだすと、多少分かりやすいでしょう。
b2=a2-a1,
b3=a3-a2,
b4=a4-a3,
bn-1=an-2-an-3,
bn=an-1-an-2
b1=a1とすると、
b1+b2+b3+・・・+bn
=a1
+(a2-a1)
+(a3-a2)
+(a4-a3)
+(a5-a4)
+・・・
+(an-2-an-3)
+(an-1-an-2)
=an-1
階差数列および類似の形の数列には色々なパターンがあるので、公式を覚えるというよりは、和をとる事で度の項が消えてどの項が残るのかを個々の計算ごとに把握するとよいでしょう。
一般の和について成立する公式
特定の形の数列に限らず、一般に和に関して成立する公式というか関係式には次のようなものがあります。
- 「和」の定数倍 $$\sum_{\large{j=1}}^n(ca_n)=c\sum_{\large{j=1}}^na_n$$
- 「和」同士の和と差 $$\sum_{\large{j=1}}^n(a_n\pm b_n)=\left(\sum_{\large{j=1}}^na_n\right)\pm \left(\sum_{\large{j=1}}^nb_n\right)$$
- 「和」同士の「積」に関する性質$$\sum_{\large{i,j=1}}^{n}\large{(a_ib_j)}=\left(\sum_{\large{i=1}}^n\large{a_i}\right)\left(\sum_{\large{j=1}}^n\large{b_j}\right)$$ $$= (a_1+a_2+\cdots +a_n)(b_1+b_2+\cdots +b_n) $$ $$\sum_{\large{i=1}}^{n}\sum_{\large{j=1}}^{m}\large{(a_ib_j)}=\left(\sum_{\large{i=1}}^n\large{a_i}\right)\left(\sum_{\large{j=1}}^m\large{b_j}\right)$$ $$=(a_1+a_2+\cdots +a_n)(b_1+b_2+\cdots +b_m)$$ ここで、\(\large{a_ib_j}\)は\(\large{a_iとb_j}\)との積です。数列の変数が2つ以上ある場合のシグマ記号を使っています。
これらのうち、最初の2つは通常の足し算の性質を式の形で書いてあるだけなのであまり公式としては認識する必要はないですが、3番目の式は注意する必要があり、しかも重要です。
「和同士の積」の計算の場合は、nとmのうちまずnだけ全部足してmは変数扱いにしておき、
その後でさらにmを動かして全体の合計の和を計算してもよいという事です。
これは、次の計算を考えると式の展開の計算通りにすると(n,m)=(1,1), (1,2), (1,3), (2,1), (2,2), (2,3),・・・の全ての組が\(\large{a_ib_j}\)の項の中に出てくる事によります。
$$(a_1+a_2+a_3+\cdots +a_n)(b_1+b_2+b_3+\cdots +b_n)$$
$$=a_1b_1+a_1b_2+a_1b_3+\cdots+a_2b_1+a_2b_2+a_2b_3+\cdots +a_3b_1+a_3b_2+a_3b_3+\cdots$$
高校数学ではほとんど扱いませんが、変数が複数ある時にシグマ記号をやたらと多く組み合わせる場合には、この「和同士の積」に関する性質を把握しておく事は結構重要になります。
