【群論】可解群の性質

可解群（solvable group）とは、群に対して交換子群列を作った時に
Ｄ_ｋ(Ｇ)＝｛ｅ｝【単位元だけからなる群】となる自然数ｋが存在する群Ｇの事です。以下、Ｄ(Ｇ)（＝Ｄ_１(Ｇ)）はＧの交換子群で、Ｄ_２(Ｇ)＝Ｄ(Ｄ_１(Ｇ))、Ｄ_３(Ｇ)＝Ｄ(Ｄ_２(Ｇ))、・・・等とします。

可解群の性質７つ

可解群のいくつかの重要な性質をまとめると次のようになります。

以下、証明をしていきます。

①可換である群は全て可解群

まず最初は簡単です。
｛ｅ｝の交換子を作ってもｅにしかならないので、交換子群列は一度｛ｅ｝になるとその先の交換子群はずっと｛ｅ｝です。可換群はそもそも任意の交換子が単位元ｅであるわけですから、「可換群は可解群である」と言えます。

②可解群の部分群も可解群

２番目については集合としての包含関係を丁寧に見て行きます。
交換子についてＨがＧの部分群であれば、Ｇの交換子群にはＨの元で作った交換子も全て含まれるので、Ｄ(Ｇ)⊃Ｄ(Ｈ)です。【交換子群列の中ではこれはＤ_１(Ｇ)およびＤ_１(Ｈ)】
すると、今度はＤ(Ｇ)の交換子群とＤ(Ｈ)の交換子群についても同じ事が言えるわけですから、Ｄ_２(Ｇ)⊃Ｄ_２(Ｈ)です。
以下同様にして任意の自然数ｊについてＤ_ｊ(Ｇ)⊃Ｄ_ｊ(Ｈ)です。
ここで、Ｇが可解群であればＤ_ｋ(Ｇ)＝｛ｅ｝となるｋが存在するので、
その番号において｛ｅ｝⊃Ｄ_ｋ(Ｈ)であり、
それを満たせるのは同じく単位元だけからなる群しかないのでＤ_ｋ(Ｈ)＝｛ｅ｝であり、従ってＨも可解群である事を意味します。

③可解群の剰余群も可解群

３番目は、剰余類と剰余群の性質を丁寧に扱う必要があります。
次にＮをＧの正規部分群として剰余群Ｇ／Ｎの交換子を考えます。
Ｇの元ｘとｙを使って、交換子群Ｄ(Ｇ／Ｎ)の元は
(Ｎｘ)^－１(Ｎｙ)^－１(Ｎｘ)(Ｎｙ)＝Ｎ(ｘ^－１ｙ^－１ｘｙ) と書けます。
【Ｄ(Ｇ／Ｎ)もまた剰余類を元とする群であり、Ｎ＝Ｎｅを単位元とする。】
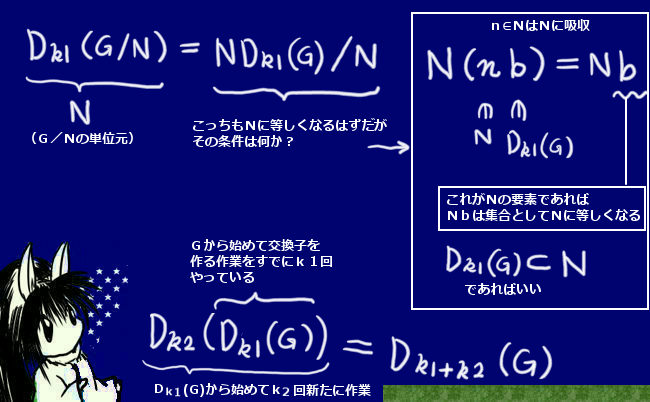
ここで２つの元の積を元とする別の群ＮＤ(Ｇ)＝｛ｎｂ｜ｎ∈Ｎ，ｂ∈Ｄ(Ｇ)｝を考えると、
これはＮを正規部分群に持つ群となりＮによる剰余群を定義できます。
【※一般に、ＨがＧの部分群で\(G\triangleright N\)である時、ＮはＮＨの部分群であり、任意のｓ∈ＮＨ（⊂Ｇ）に対してｓＮ＝Ｎｓとなる（任意のｔ∈Ｇに対してそうだから）ので、ＮはＮＨの正規部分群。
このタイプの群に対する剰余群は、(ＮＨ)／Ｎの事をＮＨ／Ｎのように書きます。】
剰余群ＮＤ(Ｇ)／Ｎの元はＮ(ｎｂ)＝(Ｎｎ)ｂですが、
Ｎが群でｎ∈Ｎに対してＮｎは集合としてはＮとして全く同じ物になるので、Ｎ(ｎｂ)＝Ｎｂ＝Ｎ(ｘ^－１ｙ^－１ｘｙ)
よって、全く同じ元を持つのでＤ(Ｇ／Ｎ)＝ＮＤ(Ｇ)／Ｎ
他方、Ｄ(Ｇ／Ｎ)の元ｕとｗを使うとＤ_２(Ｇ／Ｎ)＝Ｎ(ｕ^－１ｗ^－１ｕｗ) ですが、
剰余群ＮＤ_２(Ｇ)／Ｎの元は先ほどと同じくｎ∈Ｎを考えると
Ｎ(ｎｕ^－１ｗ^－１ｕｗ)＝(Ｎｎ)(ｕ^－１ｗ^－１ｕｗ)＝Ｎ(ｕ^－１ｗ^－１ｕｗ) となり、
Ｄ_２(Ｇ／Ｎ)＝ＮＤ_２(Ｇ)／Ｎ という事にもなります。
全く同じ論法で、任意の自然数ｊに対してＤ_ｊ(Ｇ／Ｎ)＝ＮＤ_ｊ(Ｇ)／Ｎ が成立します。
すると Ｄ_ｋ(Ｇ)＝｛ｅ｝となるｋにおいて、
ＮＤ_ｋ(Ｇ)／Ｎ の元はＮ(ｎｅ)＝Ｎｅ＝Ｎ【剰余群の単位元】ただ１つという事になり、
Ｄ_ｋ(Ｇ／Ｎ)＝ＮＤ_ｋ(Ｇ)／Ｎ＝Ｎ となってＧ／Ｎも可解群であるという結果になります。

④正規部分群Ｎと剰余群Ｇ／Ｎが共に可解群 ⇒ Ｇも可解群

次に４番目の性質ですが、これも１つ１つの式を丁寧に紐解きます。
Ｇ／ＮとＮが共に可解群である場合には、
①：Ｄ_ｋ１(Ｇ／Ｎ)＝Ｎｅ＝Ｎ　かつ
②：Ｄ_ｋ２(Ｎ)＝｛ｅ｝
となる自然数ｋ_１とｋ_２が存在します。
この時、前述において示した事からＤ_ｋ１(Ｇ／Ｎ)＝ＮＤ_ｋ１(Ｇ)／Ｎ であるわけですが、
Ｄ_ｋ１(Ｇ／Ｎ)＝ＮですからＮ＝ＮＤ_ｋ１(Ｇ)／Ｎという事になり、
実はＤ_ｋ１(Ｇ)⊂Ｎが成立しています。
【※ｎ∈Ｎおよびｂ∈Ｄ_ｋ１(Ｇ)として、ＮＤ_ｋ１(Ｇ)／Ｎの元Ｎ(ｎｂ)＝Ｎｂ は集合としてＮに等しくならないといけないので、ｂはＮの元である必要があります。それがＤ_ｋ１(Ｇ)⊂Ｎの意味です。】
すると、Ｄ_ｋ２(Ｎ)⊃Ｄ_ｋ２(Ｄ_ｋ１(Ｇ)) です。
ここで、Ｄ_ｋ２(Ｄ_ｋ１(Ｇ))とは
「すでにＧから始めてｋ_１回交換子を作る演算を行ってできた交換子群に対し、
そこを起点として改めてｋ_２回交換子を作る演算を行ってできた交換子群」です。
従って、Ｇから始めて(ｋ_１＋ｋ_２)回の交換子を作る演算を行ったＤ_{ｋ１＋ｋ２}(Ｇ)に等しいという事です。
よってＤ_ｋ２(Ｎ)⊃Ｄ_ｋ２(Ｄ_ｋ１(Ｇ))＝Ｄ_{ｋ１＋ｋ２}(Ｇ)であり、
Ｄ_ｋ２(Ｎ)＝｛ｅ｝でしたから、｛ｅ｝⊃Ｄ_{ｋ１＋ｋ２}(Ｇ) であり、
これを満たすにはＤ_{ｋ１＋ｋ２}(Ｇ)＝｛ｅ｝しかあり得ず、それを満たす自然数ｋ_１＋ｋ_２が存在する事になります。よって、おおもとの群Ｇも可解群である事になります。

この４番目の性質について、特に次のような特別な場合には１つの命題が成立します。
以下、Ｈ_ｊは群であるとします。

$$H_n\triangleright H_{n-1}\triangleright H_{n-2} \triangleright \cdots H_3\triangleright H_2\triangleright H_1\triangleright \{e\}$$

ここで、もし\(H_{j+1}\triangleright H_j\) が任意の自然数ｊについて成立し、剰余群Ｈ_ｊ＋１／Ｈ_ｊが可解群であり、
またＨ_１も可解群であったとしましょう。

そのような特別な場合が発生する時、Ｈ_１が可解群であり、Ｈ_２／Ｈ_１も可解群ですからＨ_２も可解群です。
そしてＨ_３／Ｈ_２も可解群なので、Ｈ_３も可解群です。
同様にして、任意の自然数ｊについてＨ_ｊは可解群という事になります。
より具体的には、例えば剰余群Ｈ_ｊ＋１／Ｈ_ｊが巡回群であれば可換群ですから可解群という事にもなります。そのようなタイプの群は、ベキ根で解ける多項方程式のガロア群を論じる時に出てきたりします。

⑤剰余群Ｇ／Ｎが可換群 ⇔ ＮがＤ(Ｇ)を含む事

【これは交換子群一般について言えます。性質として特に可解群に関係が深いです。】
５番目の性質については、まずＧ／Ｎの元の積を順番を変えて書いてみます。
ｘとｙをＧの元として、
(Ｎｘ)(Ｎｙ)＝Ｎ(ｘｙ) と(Ｎｙ)(Ｎｘ)＝Ｎ(ｙｘ) の２パターンありますが、
もしＮ(ｘｙ)＝Ｎ(ｙｘ)であるのなら
【※ここでの括弧は分かりすくするためにつけているだけで、Ｎｘｙ＝Ｎｙｘと書いても同じ】
ｙ^－１ｘ^－１を右から乗じる事によって
Ｎ(ｘｙｙ^－１ｘ^－１)＝Ｎ(ｙｘｙ^－１ｘ^－１) ⇔ Ｎ＝Ｎ(ｙｘｙ^－１ｘ^－１)
これが成立するためには、ｙｘｙ^－１ｘ^－１がＮの元でなければなりませんが、
ｙｘｙ^－１ｘ^－１はＧの交換子です。
【ｙｘｙ^－１ｘ^－１の逆元はｘｙｘ^－１ｙ^－１】
よって、Ｇ／Ｎが可換という事は任意のＤ(Ｇ)の元が例外なくＮの元でもある事、
つまりＤ(Ｇ)⊂Ｎを意味します。
逆にＤ(Ｇ)⊂Ｎならば
Ｎ＝Ｎ(ｙｘｙ^－１ｘ^－１) ⇔ Ｎ(ｘｙｙ^－１ｘ^－１)＝Ｎ(ｙｘｙ^－１ｘ^－１) のように逆にたどって、
右側からｘｙを乗じればＮ(ｘｙ)＝Ｎ(ｙｘ)となり、剰余群Ｇ／Ｎは可換である事になります。

⑥交換子群列の隣り合う交換子群の剰余群は可換

６番目の性質については、交換子群列において例えばＤ_２(Ｇ)⊃Ｄ_３(Ｇ)のような包含関係があり、
しかもそれらは群と正規部分群の関係にあって\(D_2(G)\triangleright D_3(G)\) のようになっています。
そこで剰余群Ｄ_２(Ｇ)／Ｄ_３(Ｇ)の可換性を調べてみると、
Ｄ_３(Ｇ)とは「Ｄ_２(Ｇ)の交換子群」なのでＤ_３(Ｇ)＝Ｄ(Ｄ_２(Ｇ)) とも書けます。
集合が（群も含めて）等号で結ばれるという事は
「Ｄ_３(Ｇ)⊃Ｄ(Ｄ_２(Ｇ))かつＤ_３(Ｇ)⊂Ｄ(Ｄ_２(Ｇ))」という事ですから、
【上述の５番目の性質により】Ｄ_３(Ｇ)⊃Ｄ(Ｄ_２(Ｇ)) ⇔「Ｄ_２(Ｇ)／Ｄ_３(Ｇ) は可換である」事になります。
同じように任意の自然数ｊとｊ＋１の交換子群についても
Ｄ_ｊ(Ｇ)＝Ｄ(Ｄ_ｊ＋１(Ｇ)) ⇒ Ｄ_ｊ(Ｇ)⊃Ｄ(Ｄ_ｊ＋１(Ｇ))
⇔「Ｄ_ｊ(Ｇ)／Ｄ_ｊ＋１(Ｇ) は可換である」という事が言えます。
可解群の場合、最後｛ｅ｝になっている部分についても同様に
｛ｅ｝＝Ｄ(Ｄ_ｋ－１(Ｇ)) からＤ_ｋ－１(Ｇ)／｛ｅ｝＝Ｄ_ｋ－１(Ｇ) が可換であるという事が言えます。
【｛ｅ｝＝Ｄ(Ｄ_ｋ－１(Ｇ))という事自体から、
交換子群の性質によりＤ_ｋ－１(Ｇ)の任意の要素は可換であるとも言えます。】

あるいは、交換子群の性質により「Ｇ／Ｄ(Ｇ)は可換である」と言えるので、
これをＤ_ｊ(Ｇ)／Ｄ_ｊ＋１(Ｇ)にも適用して示す事もできます。本質的に同じ証明です。

⑦２つの定義は同等である事

最後に７番目の性質として、２つの定義が同等である事を示します。
まず、交換子群列のほうの定義の場合での性質からＤ_ｊ＋１(Ｇ)はＤ_ｊ(Ｇ)の正規部分群であり、
剰余群Ｄ_ｊ(Ｇ)／Ｄ_ｊ＋１(Ｇ)は可換であると言えるわけですから、
そのような部分群の列が存在するので
「交換子群列の定義 ⇒ 正規部分群と剰余群の可換性のみの定義」が言えます。

次に逆の場合です。$$G=H_0\triangleright H_1 \triangleright H_2\triangleright H_3\triangleright \cdots\triangleright H_{n-1} \triangleright H_n={e}$$の関係のもとで剰余群Ｈ_ｊ－１／Ｈ_ｊが可換であったとします。
この時には「Ｇ／Ｎが可換群 ⇔ Ｄ(Ｇ)⊂Ｎ」【上記５番目の性質】である事を思い出すと、
「Ｇ／Ｈ_１が可換」なのでＤ(Ｇ)＝Ｄ_１(Ｇ)⊂Ｈ_１という事が言えます。
この時Ｄ(Ｄ_１(Ｇ))⊂Ｄ(Ｈ_１) ⇔ Ｄ(Ｈ_１)⊃Ｄ_２(Ｇ)でもあります。
【Ａ⊂Ｂ ⇒ Ｄ(Ａ)⊂Ｄ(Ｂ) 】
同様に「Ｈ_１／Ｈ_２が可換」なのでＤ(Ｈ_１)⊂Ｈ_２であり、先ほどのＤ(Ｈ_１)⊃Ｄ_２(Ｇ)と合わせると
Ｈ_２⊃Ｄ(Ｈ_１)⊃Ｄ_２(Ｇ)が成立します。
以下、同様にＨ_３⊃Ｄ_３(Ｇ)、Ｈ_４⊃Ｄ_４(Ｇ)_、Ｈ_５⊃Ｄ_５(Ｇ)_、Ｈ_ｊ⊃Ｄ_ｊ(Ｇ)・・・・と続きます。
最後の部分でＤ_ｎ(Ｇ)⊂Ｈ_ｎ＝｛ｅ｝となりますが、これはＤ_ｎ(Ｇ)＝｛ｅ｝を意味します。
よって、交換子群列の中で｛ｅ｝となる交換子群が存在するので
「正規部分群と剰余群の可換性のみの定義 ⇒ 交換子群列の定義」が言えます。
よって、２つの定義は必要十分条件で結ばれるので同等な定義である事になります。