球の表面積と体積の公式はセットになっています。微分と積分の関係で結ばれています。
微分の公式と積分の理論については別途に詳しくまとめています。
直接的な問いとして出題されるのは高校数学の範囲ですが、球の表面積や体積を種々の理論で「使う」事は大学数学と物理学でも引き続き行われます。特に物理学で円や球がモデルとしてよく使われますが、これは単純に、半径が等しいと性質が理論を組み立てる際に非常に便利であるからです。
公式
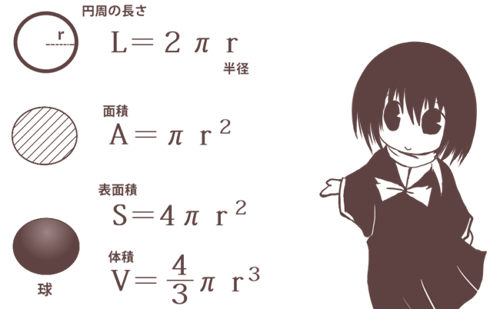
球の表面積と体積の公式は次のようになります。
$$S=4\pi r^2【球の表面積】$$ $$V=\frac{4}{3}\pi r^3【球の体積】$$ ★覚え方としては、面積は2乗、体積は3乗という点は四角形と立方体の関係と同じと考える事ができます。比例係数については微分・積分の関係にあり、円が関わりますから円周率もくっついてくるというわけです。
公式の導出については、じつは
円周の長さ → 円の面積 → 球の体積 → 球の表面積 という順番です。
しかも、基本的には微分と積分の関係で結ばれているのです。ただし微積分による導出では、順番としては体積が先でその次が表面積という事になります。

表面積公式の導出
球の体積のほうの公式の「4/3」という係数が不可解で覚えにくいという人もいるかもしれませんが、微積分を考えてみてください。球の体積公式をrで微分すると球の表面積になるのです。
これはそう考えると単に覚えやすいという事ではなくて、数学の理論としても本質的な事なのです。
$$rで微分する:\frac{d}{dr}\left(\frac{4}{3}\pi r^3\right)=4\pi r^2$$
このように、初歩的な微分の公式で体積と表面積の関係が結ばれています。
逆に表面積の公式をrで積分すれば体積の公式になりますが、これはより正確には「0からrまで」の定積分になります。しかし0の部分は代入すると消えるので、公式を覚えるという意味では結果的に考えなくてもよい事になります。

尚、積分を使えば最初に円の「面積」をいきなり出す事も計算上は可能ですが、この計算ではじつは三角関数への置換積分を利用します。そこで三角関数の微分公式を使うわけですが、肝心のこの三角関数の微分公式は、円周率が極限値として存在する事を前提としています。
そのため、この積分による面積計算は円周率という値の存在の「証明」としては、通常は使いません。ただし「理解」する方法としては有用です。また円周率の正確な数値3.14159265・・を直接計算するための手法としては、じつは周の長さよりも円の面積のほうを利用する事が多いのです。
体積公式の導出
しかし、球の体積と表面積が微積分の関係にあるとすれば、平面の円の面積と球の体積はどうつながるのか?という話になります。
微積分の関係である事は同じです。ただし、この場合は [-r,r] の積分区間での定積分になります。また、積分の設定をする際に1つだけ注意が必要です。そのため、定積分の結果である球の体積のほうから円の面積を推測するのは少々難しいでしょう。
基本的には、「断面の面積が分かっている立体」の体積を計算する要領で定積分を行って導出するのです。
直交座標上に立体をおいて、x軸に垂直な断面積をxで定積分します。
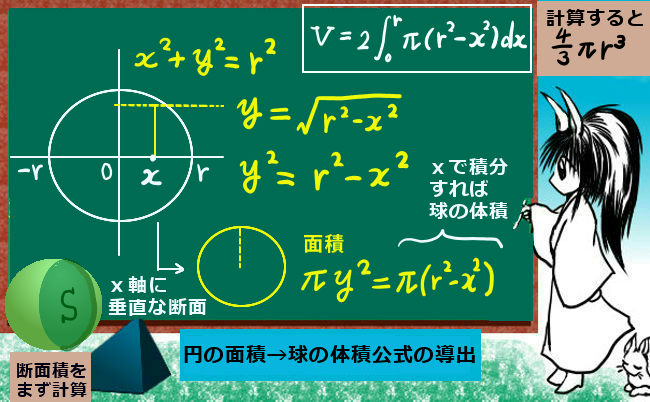
計算を簡単にするため、球の中心を原点におきます。すると、x軸に垂直な部分の断面の円の半径が分かれば、円の面積を-rから+rまで積分すれば球の体積となるのです。
その時に、xy平面の断面で一度考える必要があります。
注意点は、この時の球の、各x座標に対する断面積(円になります)と半径の考え方です。
これは、球をちょうど半分に切った時の円に対するx2+y2=r2の関係式を踏まえて、
x座標における「yの値の絶対値を半径とする」円の面積を断面積として考える必要があるのです。この設定を間違えると正しく計算されないので注意が必要です。
すると、円の式におけるyの値という事は「平方根が出てきてしまうではないか!」という事になり面倒に思えるかもしれませんが、円の面積はその2乗を考えればよいのですから、y2=r2-x2だけ分かればじゅうぶんです。
定積分の計算は次のようにします。計算は難しくありませんが、ここでの積分変数はxであり、rは定数扱いという点に少し気を付ける必要があります。
$$\int_{-r}^r\pi y^2dx=\int_{-r}^r\pi (r^2-x^2)dx=\left[r^2x-\frac{1}{3}\pi x^3\right]_{-r}^r$$
$$=r^3-\frac{1}{3}\pi r^3-\left(-r^3-\frac{-r^3}{3}\pi\right)=2r^3-\frac{2}{3}\pi r^3=\frac{4}{3}\pi r^3$$
途中の符号が入り乱れていて分かりにくい場合は、0から+rまで定積分して2倍しても同じです。
$$2\int_0^r\pi y^2dx=2\int_0^r\pi (r^2-x^2)dx=2\left[r^2x-\frac{1}{3}\pi x^3\right]_0^r$$
$$=2\left(r^3-\frac{1}{3}\pi r^3\right)=2\cdot\frac{2}{3}\pi r^3=\frac{4}{3}\pi r^3$$
この計算の仕方は球だけではなくて他の任意の立体の体積でも同じ事です。(もちろん、手計算でやる場合は原始関数を計算で出せるならの話ですが。)
物理学や工学の理論で球の表面積や体積を考える時には、特定の力等の大きさの関係と組み合わせて理論が組み立てられます。特に、距離の逆2乗に比例する(2乗に反比例する)関数と表面積の組み合わせは理論上重要な役目を果たす事になります。