静磁場では電場の場合のようにスカラーポテンシャルに相当する量を考えても統一的な物理的意味を与える事が難しくなります。(特に静磁場が電流により作られる場合。)
しかしその代わりに静磁場は発散が0になります(磁場に関するガウスの法則)。
そのため、任意の「ベクトル場の回転」の発散は0になるという公式と合わせて「回転が静磁場になるようなベクトル場」を考える事ができます。一般にそれをベクトルポテンシャルと呼びます。これはスカラーポテンシャルに対する用語というわけです。
■サイト内関連記事:
磁場に関するベクトルポテンシャルは計算を便利にするという意味合いもありますが、量子論などのように物理量としてポテンシャルのほうが重要になる場合などには本質的な重要性も持つようになったりします。
ベクトルポテンシャルとスカラーポテンシャルの関係
静磁場に対するベクトルポテンシャルを作れる数式的根拠
静電場の場合は、電位という「スカラーポテンシャル」を考えて「+1[C]の電気量の試験電荷の位置エネルギー」として物理的な意味付けもする事ができます。
それに対して静磁場の場合はポテンシャルを考える場合には普通、次のように考えます。
磁場に関するガウスの法則の微分形と、「任意のベクトル場の回転に対する発散は0になる」という公式をそれぞれ書きますと次のようになります。
$$(磁場に関するガウスの法則)\mathrm{div}\overrightarrow{B}=0$$
$$(公式)\mathrm{div}\left(\mathrm{rot}\overrightarrow{A}\right)=0$$
これらの式を見比べて、「回転が静磁場に等しくなるようなベクトル場」を考えます。それをベクトルポテンシャルと呼びます。
$$\mathrm{rot}\overrightarrow{A}=\overrightarrow{B}となるような「ベクトルポテンシャル」\overrightarrow{A}を考えます。$$
「回転の発散はゼロになる」公式の証明
上記で使った公式の証明はベクトル場\(\overrightarrow{F}=(F_1,F_2,F_3)\) の回転と発散を直接計算すると得られます。ただし、F1, F2, F3 は対象の領域でそれぞれ2階まで偏微分可能であるとします(偏微分の順序を入れ換えてよい条件。通常の関数であればあまり気にしなくて問題無し)。
$$\mathrm{rot}\overrightarrow{F}=\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z},\frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x},\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) なので$$
$$\mathrm{div}\left(\mathrm{rot}\overrightarrow{F}\right)=\frac{\partial^2 F_3}{\partial x\partial y}-\frac{\partial^2 F_2}{\partial x\partial z}+\frac{\partial^2 F_1}{\partial y \partial z}-\frac{\partial^2 F_3}{\partial y\partial x}+\frac{\partial^2 F_2}{\partial z\partial x}-\frac{\partial^2 F_1}{\partial z\partial y}=0$$
静磁場に対するベクトルポテンシャルを考える場合は、偏微分を行う対象はベクトルポテンシャルのほうなので多価関数などの通常と異なる関数などを考えない限りは問題なくこの公式も成立します。
ベクトルポテンシャルの任意性(ゲージ不変性)
ところで、上記のように想定したベクトルポテンシャルは1つだけに定まるとは限らず、むしろ何の制限もなければ非常に多くのものが存在できるのです。
例えば次のようなものです。
あるベクトル
\(\overrightarrow{A}\)が静磁場のベクトルポテンシャルになる事が分かったとしましょう。次に、そのベクトル場に渦無しの条件を満たす(つまり回転が0となる)別のベクトル場\(\overrightarrow{P}\)を加えます。すると、両者の合計\(\overrightarrow{A}+\overrightarrow{P}\)もまた「回転が静磁場を表す」ベクトル場となります。
$$\mathrm{rot}\overrightarrow{A}=\overrightarrow{B}かつ\mathrm{rot}\overrightarrow{P}=0である時$$
$$\mathrm{rot}(\overrightarrow{A}+\overrightarrow{P})=\mathrm{rot}\overrightarrow{A}+\mathrm{rot}\overrightarrow{P}=\mathrm{rot}\overrightarrow{A}=\overrightarrow{B}$$
すなわち、\(\overrightarrow{A}\) はベクトルポテンシャルであるけれども
\(\overrightarrow{A}+\overrightarrow{P}\)もまたベクトルポテンシャルであると言えるわけです。
「回転が0になる」ベクトル場の具体例は意外と簡単に見つける事ができます。普通の3変数関数を使う限りスカラー場に対しては公式 rot(gradφ)=0が成立するためです。(証明は成分ごとの直接計算により可能で、偏微分の順序入れ換えを使用。)「渦無し」の条件を満たすベクトル場としてはスカラー場の勾配と考えたほうが見通しがよくなる場合があります。
このようにベクトルポテンシャルを考えた時には複数の多くのベクトル場がそれに該当し得るわけで、言い換えると無条件では1つに限定できないという事も意味します。
上記の例のようにベクトルポテンシャルに対し1つのベクトル場を付け加える「自由度」がある時(回転=0となるものを加える場合は実質的に1つのスカラー場)、その事を指して「ゲージ不変性」と呼ぶ事があります。また、一定の条件のもとでゲージ不変性を利用してベクトルポテンシャルの変換を行う事をゲージ変換と呼びます。
$$「ゲージ変換」の1つ:\mathrm{rot}\overrightarrow{A}→\overrightarrow{A}+\mathrm{grad}\phi$$
$$(変換前と変換後とで、どちらも回転をとる操作で同じ静磁場を表します。)$$
関連して、ベクトルポテンシャルそのものに対して\(\overrightarrow{B}=\mathrm{rot}\overrightarrow{A}\) 以外に課す具体的な条件をゲージ条件と呼ぶ事があります(後述の「放射ゲージ条件」のように名前を付けて使う事が多い)。普通は、ゲージ条件を課す事によってゲージ変換の自由度が制限され、ベクトルポテンシャルも特定の形に制限されるようになります。
放射ゲージ条件(発散が0の条件)
様々なベクトル場がポテンシャルとしてあり得てしまうと理論的にかえって扱いにくくなる事もあるので、静磁場の理論においては「発散が0である」というゲージ条件を課します。
この条件を放射ゲージ条件、あるいはクーロンゲージ条件などと言います。
(「クーロンゲージの条件」のように言う事も。)
ベクトルポテンシャルに対して課す「発散が0である」という条件を
「放射ゲージ条件」または「クーロンゲージ条件」と言います。$$放射ゲージ条件:\mathrm{div}\overrightarrow{A}=0$$普通、静磁場のベクトルポテンシャルを考える場合にはこの放射ゲージ条件を付けて考えます。
放射ゲージ条件を考える場合もそうですが、基本的にはそれ以外の場合でもベクトルポテンシャルに対しては「回転が0」という条件は付けません。「ベクトルポテンシャルの回転が静磁場に等しい」という条件をまず大前提として考えていますから、ベクトルポテンシャルの回転が0であったらそれは「磁場が無い(ゼロベクトルである)」事を表すものでしかないためです。
$$静磁場においては\mathrm{rot}\overrightarrow{A}=\overrightarrow{B}の条件も、そもそも存在します。$$
静磁場に対しては発散が常に0(静磁場に関するガウスの法則)であるわけですが、放射ゲージ条件は静磁場と同じ条件をベクトルポテンシャルに対しても考えていると見る事もできます。尚、大元の静磁場の発散が0になるという条件(物理的には「湧き出しを持たない事」)は数学上は実は重要で、ベクトルポテンシャルがベクトルとして存在できる事を保証する条件になっています。
放射ゲージ条件のもとでのベクトルポテンシャルの式
放射ゲージ条件を課した状態でベクトルポテンシャルに関する式を作ると、各法則による条件等から解を出せる微分方程式を作る事ができ、その解としてベクトルポテンシャルを具体的な式で表せます。(ただしそれでも式に積分が入ってしまいます。)
電流の周囲に同心円ごとに一定の静磁場ができる事を表すアンペールの法則を考えます。これは微分形で書くと磁場の回転が電流密度ベクトルに等しいという式になります。マクスウェル方程式全体を考える時には変位電場を考える必要がありますがそれは0であるものを考えます。
$$アンペールの法則(微分形):\mathrm{rot}\overrightarrow{B}=\mu_0\overrightarrow{j}$$
電流密度ベクトルとは、定量的には「単位面積当たり」の電流を
向きも含めて考えたベクトルです。【大きさで言うとj=I/S[A/m2]】
普通、電気回路などでは電流の向きは電線に沿った1方向とその逆だけをプラスマイナスで表現すればよいのですが、電磁場も含めて電流を扱う場合にはまずは一般の3次元ベクトルとします。
アンペールの法則の式に、静磁場をベクトルポテンシャルで表した式を代入します。
$$\mathrm{rot}\overrightarrow{B}=\mu_0\overrightarrow{j}に\mathrm{rot}\overrightarrow{A}=\overrightarrow{B}を代入すると$$
$$\mathrm{rot}\left(\mathrm{rot}\overrightarrow{A}\right)=\mu_0\overrightarrow{j}$$
ところで、この場合においてはナブラを使って式を書いたほうが左辺を展開するうえで見通しがよくなります。「『ベクトル場の回転』の回転」に対する公式は存在するのですが、実は外積ベクトルの計算「『ベクトル同士の外積』との別のベクトルとの外積」に対する公式と形が一致するのです。
(ただし計算の順番に注意。\(\overrightarrow{P}\times\left(\overrightarrow{Q}\times\overrightarrow{R}\right)\) の順番での場合の公式に対応します。)
ベクトル場の回転に対して、次の公式が成立します。 $$\nabla\times(\nabla\times\overrightarrow{A})=\nabla\left(\nabla\cdot\overrightarrow{A}\right)-\nabla^2\overrightarrow{A}$$ $$\nabla\left(\nabla\cdot\overrightarrow{A}\right)=\mathrm{grad}(\mathrm{div}\overrightarrow{A})\hspace{20pt}\nabla^2\overrightarrow{A}= \frac{\partial^2\overrightarrow{A}}{\partial x^2}+ \frac{\partial^2\overrightarrow{A}}{\partial y^2}+ \frac{\partial^2\overrightarrow{A}}{\partial z^2} $$ 対応する外積ベクトルの公式は次のようになります。 $$\overrightarrow{P}\times\left(\overrightarrow{Q}\times\overrightarrow{R}\right)=\overrightarrow{Q}\left(\overrightarrow{P}\cdot\overrightarrow{R}\right)-\left(\overrightarrow{P}\cdot\overrightarrow{Q}\right)\overrightarrow{R}$$ $$\overrightarrow{P}=\overrightarrow{Q}の時には\overrightarrow{P}\times\left(\overrightarrow{P}\times\overrightarrow{R}\right)=\overrightarrow{P}\left(\overrightarrow{P}\cdot\overrightarrow{R}\right)-\left|\overrightarrow{P}\right|^2\overrightarrow{R}$$
※「ベクトルであるという状態を保ちながら」各成分に対して
「2階の偏微分を3変数で行い和をとる」操作を表す記号は慣例としては∇2しかなく、無理に grad, div 等で表す事も不可能ではないですがかえって式が複雑になります。
ただし、もし計算対象がスカラー場であれば∇2φ= div(gradφ) として書けます。ベクトル場についても、成分ごとに見るなら例えば∇2A1= div(grad A1)のように書けるのです。
そこでナブラ記号を使って計算を進めると次のようになります。
$$\mathrm{rot}\left(\mathrm{rot}\overrightarrow{A}\right)=\nabla\times(\nabla\times\overrightarrow{A})=\nabla\left(\nabla\cdot\overrightarrow{A}\right)-\nabla^2\overrightarrow{A}=-\nabla^2\overrightarrow{A}$$
$$\left( 放射ゲージ条件\nabla\cdot\overrightarrow{A}=0により\nabla\left(\nabla\cdot\overrightarrow{A}\right)=0\right)$$
$$よって、-\nabla^2\overrightarrow{A}=\mu_0\overrightarrow{j}\Leftrightarrow\nabla^2\overrightarrow{A}=-\mu_0\overrightarrow{j}$$
この式は成分ごとに見れば3つの偏微分方程式です。
これを数学的に解析する手段はありますが、物理学的に考える時はむしろ次のように解釈します。
今は静磁場について考えていますが、静電場のスカラーポテンシャル(電位)についても実は同じ形の式が成立するのです。具体的には、電場が電位の勾配を使って表される式をガウスの法則の微分形に代入します。
$$\overrightarrow{E}=-\mathrm{grad}\phi\hspace{5pt}かつ\hspace{5pt}\mathrm{div}\overrightarrow{E}=\frac{\rho}{\epsilon_0}\hspace{5pt}により、$$
$$-\mathrm{div}(\mathrm{grad}\phi)=\frac{\rho}{\epsilon_0}\Leftrightarrow\nabla^2\phi=-\frac{\rho}{\epsilon_0}$$
$$\left(\mathrm{div}(\mathrm{grad}\phi)=\mathrm{div}\left(\frac{\partial\phi}{\partial x},\frac{\partial\phi}{\partial y},\frac{\partial\phi}{\partial z}\right)=\frac{\partial^2\phi}{\partial x^2}+
\frac{\partial^2\phi}{\partial y^2}+
\frac{\partial^2\phi}{\partial z^2}=\nabla^2\phi\right)$$
ところで無限遠(電荷から十分離れた位置)を基準にすれば電位φは点電荷に対して普通に計算ができて次のようになります。
$$\phi=\int_0^{\infty}\overrightarrow{E}\cdot d\overrightarrow{r}=\int_0^{\infty}\left|\overrightarrow{E}\right|dr=\frac{kQ}{r}$$
接線線積分の段階で見れば、点電荷が複数あってそれらが作る電場の合計\(\overrightarrow{E_1}+\overrightarrow{E_2}+\overrightarrow{E_3}+\cdots\) を考えたとしても項別の積分を行って加えれば良い事が分かります。つまり複数の点電荷による電位は個々の点電荷による電位の「重ね合わせ」(スカラーの和)で計算して良い事になります。そこで、電荷が連続的に分布しているとみなせて電荷密度ρで表せるとすると次のように積分を使って書けます。
$$\phi=k\int_V\frac{\rho}{R}dv$$
この積分において R は「電位を考える点(x,y,z)」と個々の微小領域dv(=dXdYdZ)の座標との距離です。
さて、そのように電位が表せるわけですが、
この直接計算によるφは同時に先ほどの微分方程式∇2φ=-ρ/ε0を満たすわけです。
言い換えると「微分方程式の解になっている」という事になります。そして静磁場のベクトルポテンシャルに関しても成分ごとに見れば∇2A1=-j1μ0という形であるわけですから、定数の違いを除くと「同じ形の微分方程式」であり、解も「電位を電荷密度で表す式と同じ形になる」と見るのです。
(これらのような∇2u(x,y,z)=-v(x,y,z) の型の微分方程式を総称して「ポアソン型の微分方程式」とか「ポアソン方程式」などと呼ぶ事もあります。)
$$ベクトルポテンシャルの成分ごとにA_1=K\int_V\frac{j_1}{R}dvの形になるはずであり、$$
$$ベクトルでは\overrightarrow{A}=K\int_V\frac{\overrightarrow{j}}{R}dv$$
これが放射ゲージ条件のもとでの静磁場のベクトルポテンシャルを表す式になります。より具体的な関数形は、電流密度の関数形と分布領域によって変わってきます。
(数式だけでポアソン型の微分方程式を解く場合には、ガウスの発散定理から証明できる「(実関数についての)グリーンの定理」を使用します。)
上式では比例定数はkおよびKなどと書きましたが、真空の誘電率と透磁率を使って改めて書いて整理すると次のようになります。
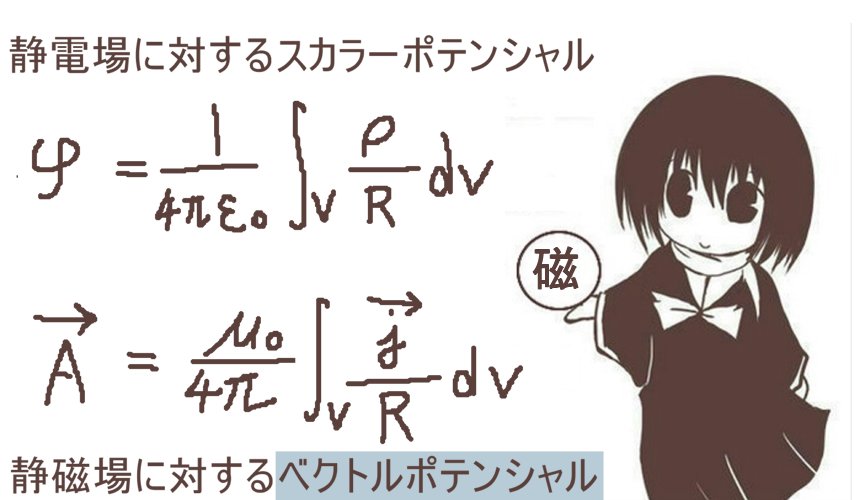
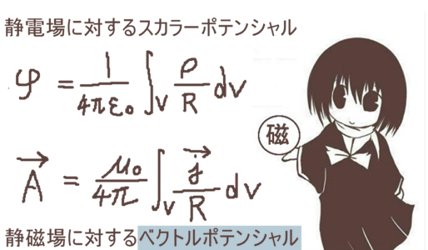
静電場がスカラーポテンシャル(電位)を持つのに対して、
静磁場はベクトルポテンシャルを持ち、それぞれの式は次のように書けます。
$$静電場のスカラーポテンシャル:\phi=\frac{1}{4\pi\epsilon_0}\int_V\frac{\rho}{R}dv$$
$$静磁場のベクトルポテンシャル:\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_V\frac{\overrightarrow{j}}{R}dv$$
ε0は真空の誘電率、μ0は真空の誘磁率です。
ρは電荷密度、\(\overrightarrow{j}\)は電流密度ベクトルでいずれも「分布」の意味での位置の関数(x,y,zの3変数関数)です。
Rはポテンシャル(スカラー・ベクトルともに)を考える位置と
微小領域dv(dxdydzと考えても同じ)を代表する位置との距離で、より数式的にそれを明示するならそれぞれの位置を\(\overrightarrow{r}\)および\(\overrightarrow{R}\) として\(R=\left|\overrightarrow{r}-\overrightarrow{R}\right|\) のように書きます。それぞれの位置を表す座標は、式に積分が含まれている事に由来して上式では互いに独立した3変数の組として扱うので注意。例えば(x,y,z)と(X,Y,Z)のように何らかの表記で区別します。(その場合 dv =dXdYdZ として計算し、積分の結果は x, y, z の関数になります。)