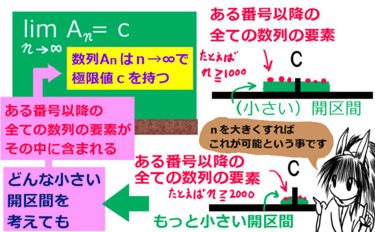
今回は、高階微分と、その応用として重要なテイラー展開、マクローリン展開と呼ばれる無限級数展開について説明します。大学で物理や工学を学ぶ場合などは、非常に重要となる項目です。
★このページの中盤以降では、マクローリン展開の事は Mcl .展開と略記します。
まず、高階微分について簡単に説明し、その応用としてテイラー展開とマクローリン展開について述べます。最後に、関数がテイラー展開可能である条件として、数学的には剰余項と呼ばれるものが収束する必要があるので、その問題について述べます【これは数学上の問題で、物理等にはあまり関係のない問題です】。
後半、数学的にかなり詳しく述べている部分もありますが、詳しい証明や導出を知りたい人向けです。
そうでない場合は参考までに眺めていただければじゅうぶんです。
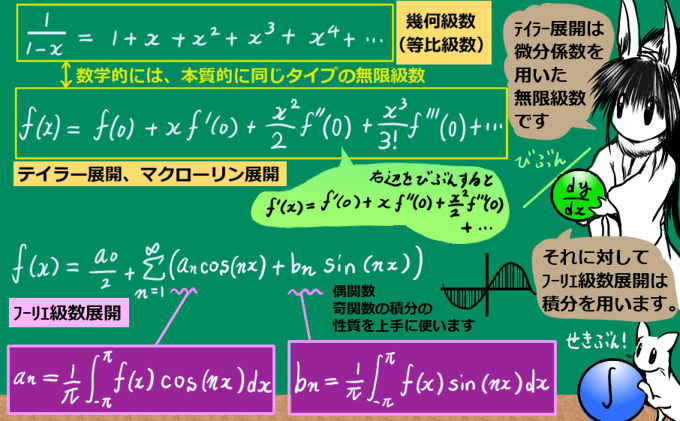
今回はテイラー展開とマクローリン展開です。高階微分を用いた無限級数展開です。
高階微分とは?
「高階微分」=「1つの関数を何度も微分する事」です。意味としては簡単ですので具体例などを見てみましょう。記号で書かれるとややこしく見えるところにだけ注意しましょう。
■ 2階微分とは?高階微分(2階微分、3階微分・・)について
■ 極限としての2階微分(2階導関数)および高階導関数の定義
2階微分とは?高階微分(2階微分、3階微分・・)について
2階微分とは、「2回」微分操作をするという事です。 同じく、3回微分操作した場合を3階微分、n回微分したも場合をn階微分と言い、まとめて高階微分と呼びます。導関数については、「n階導関数」のように表現します。
※たまたま日本語では「2階」と「2回」が同じ読み方なのでどちらで表現してもほとんど誤解はないと思いますが、一応用語としては区別されています。

例えば sin x の通常の微分(1階微分)は cos x ですが、
2階微分は -sin x で、3階微分は -cos x 、4階微分は sin x です。
- sin x → cos x [1回目の微分(=通常の微分、1階微分)]
- cos x → -sin x [2回目の微分(=2階微分)]
- -sin x → -cos x [3回目の微分(=3階微分)]
- -cos x → sin x [4回目の微分(=4階微分)]※元の関数に戻るわけです。
\(x^2\)の通常の微分(1階微分)は 2x であるわけですが、
2階微分は 2 で、3階微分は 0 です。(4階以上の微分も、全て 0 です。)
- \(x^2 \rightarrow 2x\) [1階微分]
- 2x → 2 [2階微分]
- 2 → 0 [3階微分]※定数の微分ですから、0ですね。
\(e^x\)は、1回微分すると \(e^x\) で元の関数と同じなので、
それをさらに微分した2階導関数も3階導関数も、全ての高階導関数について同じ形で \(e^x\) です。
このように、続けて公式を適用していけばいいだけなので、計算としては特別難しいものではありません。
ただ、数式としての表記方法だけ見ると、慣れないと少し難しく「見える」かもしれません。 しかし、意味するものは通常の微分の延長にあるだけという事が分かると、なじみやすいかと思います。
極限としての2階微分(2階導関数)および高階導関数の定義
極限として2階微分を考えた時の定義は次のようになります。「通常の微分(導関数)」をさらに微分するわけですので、1階微分の定義の関数の部分に、1階導関数を当てはめれば2階微分により得る2階導関数になります。
これが、2階微分(あるいは2階導関数)を定義で表した場合の式です。
初等関数に適用する場合などは、上記の例のように、公式により出されている1階の微分による導関数を単純に「もう1回」微分する事が行われるのが普通です。
3階、4階・・の微分についても、同様に考えます。例えば3階微分を定義式で(敢えて)表すのであれば次のような式になります。
高階微分の表記方法
ある関数を2階微分している事を表す表記方法は、通常の1階微分にいくつもの表記方法があるように、同じく多くの表記方法があります。基本的には1階微分の表記方法に基づくものです。
$$2階微分の表記法:\frac{d^2y}{dx^2},\frac{d^2}{dx^2}f(x),\frac{d^2f}{dx^2},\frac{d^2f(x)}{dx^2},y^{\prime\prime},f^{\prime\prime}(x),f^{(2)}(x),d^2y/dx^2, \ddot{y}$$ 3階微分、n階微分の場合の表記方法は次の通りです。 $$3階微分の表記法:\frac{d^3y}{dx^3},\frac{d^3}{dx^3}f(x),\frac{d^3f}{dx^3},\frac{d^3f(x)}{dx^3},y^{\prime\prime\prime},f^{\prime\prime\prime}(x),f^{(3)}(x),d^3y/dx^3$$ $$n階微分の表記法:\frac{d^ny}{dx^n},\frac{d^n}{dx^n}f(x),\frac{d^nf}{dx^n},\frac{d^nf(x)}{dx^n},f^{(n)}(x),d^ny/dx^n$$基本的には何階であっても表記の考え方は同じであるわけですが、階数が増えると、f(x) に「’ (プライム、ダッシュ)」をつける方法や、y の上に「・(ドット)」をつける方法は分かりにくいので、\(\frac{d^ny}{dx^n} や f^{(n)}(x)\)の表記が使われる事が多いのです。
高階導関数の表記方法を用いると、具体的な初等関数の2階微分やn階微分も、
$$\frac{d^2}{dx^2}\sin x=\frac{d}{dx}\cos x=-\sin x\hspace{10pt}\frac{d^n}{dx^n}e^x=e^x$$
・・というふうに書けます。こういう書き方をすると難しく見えてしまうかもしれませんが、
重要なのは「決められた回数だけ微分操作を繰り返している」という事なのです。
もしとっつきにくいと感じた方も、そのように易しい形で理解していただければと思います。
高階微分って、何に「使う」の??
「2階以上の微分」というものは、一見すると何に使うのか分かりにくいかもしれません。
具体例を見てみるのが、最も分かりやすいと思います。
例えば、「2階微分」を用いる最も簡単な応用例は、物理の力学の「運動方程式」です。
物理では、時間を変数としたうえで、次の解釈が適用される事が重要です。
- 速度は位置座標の1階の時間微分:\(v=\frac{dx}{dt}\)
- 加速度は位置座標の2階微分(速度の1階微分):\(a=\frac{d^2x}{dt^2}=\frac{dv}{dt}\)
※ここでの a は、定数ではなくて、加速度(acceleration)です。
※細かい事を言いますとじつは物理では「ベクトルの微分」を考えるのですが、ここでは簡単のため1次元の速度と加速度を例として挙げています。
「運動方程式を解く」という事は、「2階の微分を含む『微分方程式』」を解くという事ですので、例えばそこで2階微分の考え方が用いられるわけです。
また、このページで次に述べるテイラー展開も物理や各種の工学などで重要です。これは1階および高階の微分を用いた無限級数による関数の表現方法になります。
テイラー展開とマクローリン展開
高階微分の応用として重要なテイラー展開とマクローリン展開について述べましょう。
数学的には、1段階前のテイラー公式というものがある事が重要です。
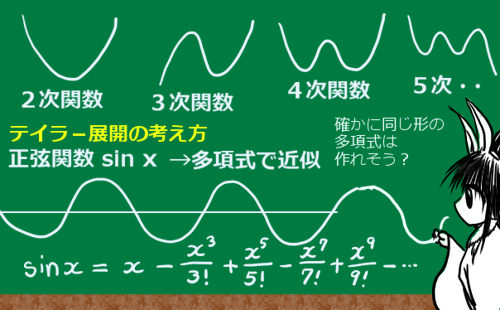
微分法はそもそも、関数のある点の近傍における近似1次式としての意味があります。そこで、1次式だけでなく、2次式、3次式の近似や、最終的には無限項の多項式で関数を近似しようという発想で、関数を多項式によって無限級数展開するのが、テイラー展開です。(平均値の定理の拡張と見る事もできます。)
■ テイラー展開とは? ■ マクローリン展開の一覧表 ■ テイラー公式の証明
関数の x = a における「テイラー展開」とは?
このテイラー展開では、通常の微分と、高階微分による微分係数(x = a におけるf'(a), f”(a)など)が用いられます。一見とっつきにくいかもしれませんが、具体的な初等関数のテイラー展開は、このページの前半でも述べた微分公式を使って係数を出していけばいいだけですので、決して難しいわけではありません。
この形で表された無限級数展開を、x = a におけるテイラー展開と言います。
このようなテイラー展開を行う時、「x = a のまわりでテイラー展開する」という言い方もします。
これは、テイラー展開が x = 0, x = 1, x = 2, ・・など、任意の x の値における微分係数で表現できるという事です。
注意と参考:数学的には「剰余項」を含む段階の「テイラー公式」があります
解析学的においては、上記の形の式が n で終わる有限項の和に「剰余項」Hn(x)を加えたものをまず考えます(テイラー公式と呼ばれる事があります)。この剰余項が n→∞ でゼロになればテイラー展開の形になります。
$$テイラー公式:f(x)=\left(\sum_{j=0}^{n}\frac{(x-a)^j}{j!}f^{(j)}(a)\right)+H_n(x)$$
初等関数では多くの場合に、この剰余項は n →∞ の極限で 0 になるので応用の面ではそこまで気にしなくてもいいのですが、収束する「xの範囲」が限定される場合もあります。
この剰余項の収束問題については、このページの後半で詳しく説明しましょう。
テイラー展開の式に \(a=0\)を代入したものがマクローリン展開と呼ばれる公式です。
x=0におけるテイラー展開がマクローリン展開です。
x=0における微分係数、高階微分係数を考えます。
★以下、マクローリン展開の事は Mcl .展開と略記します。
Mcl . 展開は、「テイラー展開の中でも、特によく用いられる形」・・という事になりますが、その理由は単純で、式の形が簡易になるためです。x = 0 という使いやすい場所での計算をしたいがため、物理などでも多く使われるのです。
物理等では、よほどの精度を求めない限り、3次や4次などの高階の部分は「ほとんど0」とみなせる場合をわざと考察する事も多いです。
指数関数や三角関数の Mcl .展開は、物理等への応用でも純粋数学的にも重要です。
例えば、ほんの1例ですが、自然対数の底 e の値が2.718・・である事や無理数・超越数である事の証明には Mcl .展開を用います。半端な変数における三角関数の具体的な値を知るのにも Mcl .展開を使えます。
$$e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots$$
$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$$
$$\cos x=1-\frac{x^2}{2}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots$$
参考までに、テイラー展開には、大学数学の解析学的には「一意性」がある事が重要です。どういう事かと言いますと、同じ「『多項式の形』の無限級数」(整級数と言います)で表される関数がある場合、同じ関数を表すのであれば、各\(x, x^2, x^3, \cdots\)の係数の表し方は「1通りしかない」という数学的事実があるのです。
(※微分以外の方法では決して表せないという事ではなくて、微分以外の方法で表せたとしても、じつは微分で表したテイラー展開に一致する、という意味です。)
これは、微分の範囲を複素数まで広げた場合などで、結構理論的には重要になります。
テイラー展開の一意性については、じつは\(f(x)=A_0+A_1(x-a)+A_2(x-a)^2+\cdots\) の形の無限級数を微分したうえでx→ a の極限を考えれば、かなり簡単に分かる事なのです。
そのように無限級数を直接微分する事を「項別微分」と言います。
しかし、じつはこの項別微分という計算は「できる場合とできない場」合があります。
\(f(x)=A_0+A_1(x-a)+A_2(x-a)^2+\cdots\) の形の無限級数(整級数と言います)は、「一様収束性」という性質があるので項別微分が可能なのです。これについては自明ではないので解析学的な証明が必要です。
\(\frac{1}{1-x}\)のテイラー展開と幾何級数展開は、本質的に同じもの?違うもの?
「高校でも教わる無限級数展開」として、幾何級数展開があります。「等比数列の和」という名前のほうが、多くの方にとって、もしかするとなじみがあるかもしれません。
例えば次の無限級数は、幾何級数の方法で出す事ができます。
$$|x| < 1 の時、\frac{1}{1-x}=1+x+x^2+x^3+x^4+\cdots$$ $$※導出:S_n=1+x+x^2+x^3+\cdots+x^n として S_n-xS_n=1-x^{n+1} となるので$$ $$|x|<1 の時、S_n(1-x)=1-x^{n+1}\Leftrightarrow S_n=\frac{1-x^{n+1}}{1-x}\rightarrow \frac{1}{1-x}\hspace{5pt}(n\rightarrow \infty)$$
このとき、じつは\(\frac{1}{1-x}\)をテイラー展開・Mcl.展開する事もできます。この時、結論を言いますと、幾何級数で表された無限級数は、Mcl.展開に一致するのです。
2つ以上の方法で整級数の形に表わせたとき(例えば幾何級数の方法とテイラー展開)であろうと、両者は本質的に同じである・・という事の具体例になります。
整級数の形に無限級数展開を行う時、何かしら「計算しやすい方法」で1つの形を導出してけば、それは本質的に1通りの正しい整級数の表式という事が、じつは保証される、という数学的事実があります。
テイラー展開等が特別扱いというわけではなく、\(\frac{1}{1-x}\)の場合であれば幾何級数によって考えるほうが簡単なので、そちらの考え方でもよいというわけなのです。
マクローリン展開の一覧表
物理等では重要なので、主要な初等関数の Mcl. 展開をいくつか表にまとめてあります。x = 0 での f(0) と、微分係数 f ‘ (0), f ‘ ‘ (0),・・を具体的に計算し、 Mcl. 展開の式に代入すれば公式が得られます。
表にある「収束半径」とは、無限級数が有限の値に収束する「変数 x の範囲」の事で、ここでのより具体的な意味としては剰余項が収束するかという事です。これについては、初等関数の中でも、あまり気にしなくてよいものと、気にしたほうがよいものがあります。
| 対象の関数 | Mcl.展開 | 収束半径 | 計算方法 |
|---|---|---|---|
| e の指数関数 | \(e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\cdots\) | 実数全域 | \((e^x)^{\prime}=\frac{d^n}{dx^n}e^x=e^x\) f(0) = f'(0) = f”(0) = 1 |
| 自然対数関数 ln(1+x) | \({\small\ln (1+x)}\) \(=x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+\cdots\) ※ln x だと、x = 0 で定義できず、微分不可能・Mcl.展開不可能 | |x| < 1 | \({\small(\ln(1+x))^{\prime}}=\frac{1}{1+x}\) \({\small(\ln(1+x))^{\prime\prime}}=\frac{-1}{(1+x)^2}\) f(0)=0, f'(0)=1, f”(0)=-1 |
| 三角関数 (正弦) | \(\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots\) | 実数全域 | \({\small(\sin x)^{\prime}=\cos x }\)
\({\small(\sin x)^{\prime\prime}=-\sin x}\) f(0)=0, f'(0)=1, f”(0)=0, f”(0)=-1 |
| 三角関数 (余弦) | \(\cos x=1-\frac{x^2}{2}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots\) | 実数全域 | \({\small(\cos x)^{\prime}=-\sin x}\)
\({\small(\cos x)^{\prime\prime}=-\cos x}\) f(0)=1, f'(0)=0, f”(0)=-1, f”(0)=0 |
| \(\frac{1}{1-x}\) 幾何級数 |
\(\frac{1}{1-x}\) \(=1+x+x^2+x^3+x^4+\cdots\) | |x|<1 | \(\left(\frac{1}{1-x}\right)^{\prime}=\frac{1}{(1-x)^2}\)
\(\left(\frac{1}{1-x}\right)^{\prime\prime}=\frac{2}{(1-x)^2}\) ※(-1)と(-1)がかけられ、 必ず+になります。 f(0)=1, f'(0)=1, f”(0)=1, f”(0)=1 |
| \((1+x)^a\) 一般2項級数 |
\((1+x)^a=1+ax\) \( +\frac{a(a-1)}{2}x^2+\frac{a(a-1)(a-2)}{3!}x^3+\cdots\) | |x|<1 | \({\small((1+x)^a)^{\prime}=a(1+x)^{a-1}}\)
\({\small((1+x)^a)^{\prime\prime}=a(a-1)(1+x)^{a-2}}\) f(0)=1, f'(0)=a, f”(0)=a(a-1) f”'(0)=a(a-1)(a-2) |
テイラー展開の式は、どのように導出する??
証明の方法はいくつかありますが、ここでは積分の公式である「部分積分」を使う方法を、述べます。(積分区間に変数を含んだ形の計算になるので注意してください。
ここで具体的に述べますのは、「剰余項」を含んだ「テイラー公式」の証明です。
そして個々の関数について、剰余項が n→∞ でゼロになる事を示して個々の関数についてのテイラー展開と Mcl. 展開が証明されるという流れです。剰余項の収束問題については後述します。
まず、
\(f(x)-f(a)=\int_a^x f^{\prime}(t)dt \Leftrightarrow f(x)=f(a) + \int_a^x f^{\prime}(t)dt\)
【※これは「微積分学の基本定理」を用いています。唐突に t という別の変数が出てきてどういう事かと思われる方もいるかもしれませんが、これはあくまで積分での表記方法の約束です。】
次に、
\(f(x)=f(a) + \int_a^xf^{\prime}(t)dt\)
\(
=f(a)-\int_a^x(x-t)^{\prime}f^{\prime}(t)dt \hspace{10pt}【∵\frac{d}{dt}(x-t)=-1】
\)
\(
=f(a)-\left[(x-t)f^{\prime}(t)\right]_a^x +\int_a^x(x-t)f^{\prime}(t)dt
\)
\(
=f(a)+(x-a)f^{\prime}(a)-\int_a^x\left(\frac{d}{dt}\frac{(x-t)^2}{2}\right)f^{\prime}(t)dt \hspace{10pt}【∵\frac{d}{dt}(x-t)^2=-2(x-t)】
\)
\(
=f(a)+(x-a)f^{\prime}(a)-\left[\frac{(x-t)^2}{2}f^{\prime}(t)\right]_a^x+\int_a^x\frac{(x-t)^2}{2}f^{\prime\prime}(t)dt
\)
\(
=f(a)+(x-a)f^{\prime}(a)+\frac{(x-a)^2}{2}f^{\prime}(a)-\int_a^x\left(\frac{d}{dt}\frac{(x-t)^3}{3!}\right)f^{\prime\prime}(t)dt
\)
\(
=f(a)+(x-a)f^{\prime}(a)+\frac{(x-a)^2}{2}f^{\prime}(a)-\left[\frac{(x-t)^3}{3!}f^{\prime\prime}(a)\right]+\int_a^x\left(\frac{d}{dt}\frac{(x-t)^3}{3!}\right)f^{\prime\prime\prime}(t)dt
\)
\(
=f(a)+(x-a)f^{\prime}(a)+\frac{(x-a)^2}{2}f^{\prime}(a)+\frac{(x-a)^3}{3!}f^{\prime\prime}(a)+\int_a^x\frac{(x-t)^3}{3!}f^{\prime\prime\prime\prime}(t)dt\)
\(=\cdots\)
この操作を繰り返す事により、\(\int_a^x\frac{(x-t)^{n-1}}{(n-1)!}f^{(n)}(t)dt\)の形の剰余項(「積分型の剰余項」)を含んだ形の「テイラー公式」が成立します。【証明終り】
この剰余項は、主要な初等関数の場合は0に収束するのでテイラー展開が成立します。ただし、剰余項が収束する「x の範囲」が限定される場合もあるので、そこは注意が必要です。
e の指数関数や、三角関数については定義域の全域で剰余項は0に収束するので、定義域全域で「テイラー展開可能」です。
この他に、計算は結構面倒なのですが、逆三角関数の Mcl.展開はじつは数学的には特徴的な形になって、円周率を表す式の導出に使えたります。ただしこれは、物理等への応用ではあまり重要ではないです。
剰余項の収束問題
上記のような部分積分による方法でも他の方法でも、テイラー展開を導出すると最後のnを含んだオマケの項である「剰余項」がくっついてきます。
結論を言うと指数関数や三角関数などの初等関数においては剰余項はn→∞で0に収束するので、無限級数の形で問題なくテイラー展開・ Mcl.展開を、使う事ができます。ここでは、その事の証明を記しておきます。結構面倒な部分も含まれるので、参考までに見てください。
■ \(e^x,\sin x,\cos x\) の剰余項の収束問題 ■ 関数 \((1+x)^{\alpha}\) の剰余項の収束問題
\(e^x,\sin x,\cos x\) の剰余項の収束問題
上記で、理論的にはまずテイラー公式というものがあって、n→∞で剰余項が0に収束するものが「テイラー展開可能」という事でした。
e の指数関数や三角関数については、剰余項が収束する事を証明してみましょう。
ポイントは、「nに関する極限」を考える事です。つまり、変数xについては極限操作としてはいじらないという事です。
極端な話、例えばx=0、x=100といった具体的な値を代入してみて、その時に剰余項がnに関してn→∞で0に収束すれば、「x=0、x=100でテイラー展開可能」という事です。
積分型の剰余項では積分区間にxが入ってますが、nに注目した場合は特定の積分区間での定積分のように考える事ができるのがポイントなのです。
前半でも触れましたように e の指数関数や三角関数はn階導関数を容易に表せます。これによってまず、剰余項のn階微分のところが具体的になります。
まず最初は、e の指数関数です。
$$e^x のテイラー公式の積分型の剰余項は:R_n(x)=\int_a^x\frac{x^{n-1}}{(n-1)!}e^tdt$$
$$注目すべきところはnに関する部分、つまり \frac{x^{n-1}}{(n-1)!}です。$$
具体的な関数の部分については各々の変数について「nに関しては定数」という扱いになり、積分も各々のxに対して有限の区間内の定積分とみなせますから、積分の中身がn→∞で0に収束すれば定積分も0に収束するのです。
$$よって、\lim_{n\to \infty}\frac{x^n}{n!}=0を示せばよく、 $$
$$それによりe^x は全実数の範囲でテイラー展開可能である事が示されます。 $$
nをじゅうぶん大きくすればおそらく0に収束する「だろう」事が予想されますが、具体的にそれを示しましょう。まずxが正の範囲の時に示します。xよりも大きいてきとうな自然数 Mを考えます。n=2Mを考えると、分母には、M+1、M+2、・・M+Mという、M個のMより大きい数が因数として含まれています。
他方、分子にあるのはMよりも小さいxという正の実数のM乗です。この時点でまず分子よりも分母が確実に大きい事が分かりますが、このn= 2Mよりもさらにnを大きくすると、nが1増えるごとに分子はxが1つ乗じられ、分母は2M+1、2M+2、・・などの数が乗じられます。つまり、nを大きくすれば、どのような小さい正の実数よりも \(\frac{x^n}{n!}\) を小さくできます。
$$x>0の時、任意の正の実数\epsilon に対し\frac{x^n}{n!}< \epsilon つまり \lim_{n\to \infty}\frac{x^n}{n!} =0 です。$$
xが負の場合も、絶対値は変わりませんから符号が入れ替わりながら0に収束します。x=0の場合は\(\frac{0^{n-1}}{(n-1)!}=0\) ですから、この場合も組み込む事ができます。
$$ よって、任意の実数xに対して\lim_{n\to \infty}\frac{x^n}{n!}=0であり、 \lim_{n\to \infty} R_n(x) =0【証明終り】 $$
三角関数の場合は、n階微分も三角関数の形ですから、絶対値は1よりも小さい事を用いて不等式を作ります。そして指数関数の時と同様の極限を考える事で剰余項がn→∞で0に収束する事になるのです。
関数 \((1+x)^{\alpha}\) の剰余項の収束問題
じつは剰余項の収束問題に関しては、e の指数関数や三角関数よりも\((1+x)^{\alpha}\)といった一見簡単な関数のほうが、証明が面倒です。
おそらく、このページの内容の中では問題としてはここが一番難しいです。
上手に不等式を使って値の大きさを評価しないと、なかなかうまくいきません。
ここでは、次の事を示します:
$$任意の実数\alpha に対して(1+x)^{\alpha} は、|x|<1ならば Mcl. 展開可能$$
「|x|<1 の範囲で、x=0のまわりでテイラー展開可能」と言っても同じです。
以下、x=0のまわりでのテイラー公式について考えます。Mcl.展開の形で「無限級数ではなく剰余項が残ったままの状態」と考えてもよいと思います。
$$ f(x)=(1+x)^{\alpha} の積分型の剰余項:R_n(x)=\int_0^x\frac{(x-t)^{n-1}}{(n-1)!}f^{(n)}(t)dt$$
$$f(x)=(1+x)^{\alpha}とすると、 f^{(n)}(t)=\alpha (\alpha -1)(\alpha -2)\cdots(\alpha -n+1) (1+t)^{\alpha -n} $$
積分変数(ここではt)に対する定数となる部分は、積分記号の前に持っていきましょう。
$$ R_n(x)= \frac{ \alpha (\alpha -1)(\alpha -2)\cdots(\alpha -n+1) }{ (n-1)! } \int_a^x (x-t)^{n-1} (1+t)^{\alpha -n} dt $$
不等式をうまく使うために、2つほど、それほど難しくない関係式を示します。まず、1つ目です。
$$|x|<1 かつ 0<t<xまたは0>t>xならば\left|\frac{x-t}{1+t}\right|<|x|$$ ちょっと分かりにくいかと思いますが、xとtの正負の符号が一致して、尚かつ絶対値に関して|x|>|t| という関係のもとで成立する式です。これは、積分に関してうまく不等式を作るための式です。
★ 証明: $$0<t<xの時、\left|\frac{x-t}{1+t}\right|=\frac{x-t}{1+t}<\frac{x}{1+t}<x=|x|$$ $$0>t>xの時、\left|\frac{x-t}{1+t}\right|=\frac{-x+t}{1+t}<\frac{-x-xt}{1+t}=\frac{-x(1+t)}{1+t}=-x=|x|【証明終り】$$ 2番目のほうについては、x >-1 に―t(>0)を乗じた ―xt>tの関係を使っています。
これによって剰余項を次のように変形したうえで不等式で評価できます。
$$ R_n(x)= \frac{ \alpha (\alpha -1)(\alpha -2)\cdots(\alpha -n+1) }{ (n-1)! } \int_a^x (x-t)^{n-1} (1+t)^{\alpha -n} dt$$
$$= \frac{ \alpha (\alpha -1)(\alpha -2) \cdots (\alpha -n+1) }{ (n-1)! } \hspace{5pt}\int_a^x \left(\frac{x-t}{1+t}\right)^{n-1} (1+t)^{\alpha -1} dt $$
これに絶対値をつけます。不等式を作りやすくなるためです。
次の式の2段目から3段目への不等式を作るために上記の補題の結果を用いています。
$$ |R_n(x) |= \left | \frac{ \alpha (\alpha -1)(\alpha -2) \cdots (\alpha -n+1)}{ (n-1)! } \hspace{5pt} \int_a^x \left(\frac{x-t}{1+t}\right)^{n-1} (1+t)^{\alpha -1} dt\right|$$
$$< \frac{ | \alpha (\alpha -1)(\alpha -2)\cdots(\alpha -n+1) |}{ (n-1)! } \int_a^x \left| \frac{x-t}{1+t}\right|^{n-1} |1+t|^{\alpha -1}dt $$
$$< \frac{| \alpha (\alpha -1)(\alpha -2) \cdots (\alpha -n+1)|}{ (n-1)! } \hspace{5pt} \int_a^x |x|^{n-1} |1+t|^{\alpha -1}dt $$
$$=\frac{| \alpha (\alpha -1)(\alpha -2) \cdots (\alpha -n+1)|}{ (n-1)! } |x|^{n-1} \hspace{5pt} \int_a^x |1+t|^{\alpha -1}dt $$
この最後の式には積分の中身にはnが入っていませんから、nに関しては定数であると考えて(もちろん各々のxに対しては別々の値になります)、てきとうにCとおけます。絶対値を外せば積分の計算も直接できてしまいますが、ここでは「nに関して定数」である事が分かればじゅうぶんなのです。まとめると次のようになります。
$$|R_n(x)|< \frac{ |\alpha (\alpha -1)(\alpha -2)\cdots (\alpha -n+1) |}{ (n-1)! } |x|^{n-1} C$$
この不等式の右辺側をもう少し変形します。
$$\frac{ |\alpha (\alpha -1)(\alpha -2) \cdots (\alpha -n+1) |}{ (n-1)! } |x|^{n-1} C$$
$$=\frac{| \alpha (\alpha -1)(\alpha -2) \cdots (\alpha -n+1) |}{ 1・2・3・4 \cdots (n-2)(n-1)} |x|^{n-1} C$$
$$< \frac{| \alpha (\alpha +1)(\alpha +2) \cdots (\alpha +n-1) |}{ 1・2・3・4 \cdots (n-2)(n-1)} |x|^{n-1} C $$
$$=|\alpha|\left(1+\frac{| \alpha |}{1} \right ) \left (1+\frac{| \alpha |}{2} \right ) \left (1+\frac{| \alpha |}{3} \right ) \cdots \left (1+\frac{| \alpha |}{n-1} \right ) |x|^{n-1} C $$
ここで、先に進むにはもう1つ補題が必要です。
$$任意の実数\alpha に対して、0<r<1 ならば1+\frac{|\alpha|}{N}<\frac{1}{r} となる自然数Nが存在する$$ これは何の事かと言うと、要するに1と1よりも大きい数の間には1+εという別の数が必ずあり、大きい自然数Nで割る事でそのような小さい数εを作れる事を、式で表しただけです。
★ 証明: $$1<\frac{1}{r} であり、1<1+\epsilon <\frac{1}{r}を満たす正の実数\epsilon が必ず存在する。$$ $$任意の実数\alpha に対して0<\frac{|\alpha|}{N}<\epsilon となる(十分大きい)自然数Nは存在できる。$$ $$よって、 1+\frac{|\alpha|}{N}<1+\epsilon <\frac{1}{r}となる自然数Nが存在する。【証明終り】$$
これによって、さらに別の不等式で評価ができます。0<|x|<r<1を満たすてきとうな実数 r を想定します。
$$1+\frac{|\alpha|}{N}<\frac{1}{r} となる自然数Nが存在し、n≧N ならば 1+\frac{|\alpha|}{n}<\frac{1}{r}でもある。$$
$$n≧N の時、R_n(x)<|\alpha|\left(1+\frac{| \alpha |}{1} \right ) \left (1+\frac{| \alpha |}{2} \right ) \left (1+\frac{| \alpha |}{3} \right ) \cdots \left (1+\frac{| \alpha |}{N} \right ) \cdots \left (1+\frac{| \alpha |}{n-1} \right ) |x|^{n-1} C$$
$$< |\alpha|\left(1+\frac{| \alpha |}{1} \right) \left (1+\frac{| \alpha |}{2} \right ) \left(1+\frac{| \alpha |}{3} \right) \cdots \left(1+\frac{| \alpha |}{N-1} \right) |x| ^{N-1} \left(\frac{ |x| }{r}\right)^{n-N-1} C $$
この不等式評価は、ある自然数Nについて、N-1までの項はそのままにして、N以降の項は1/rよりも小さいとしているのです。
ここで、N-1までの項の積は、nに関して定数である事に注意します。
$$つまり、 |\alpha|\left(1+\frac{| \alpha |}{1} \right ) \left ( 1+\frac{| \alpha |}{2} \right ) \left (1+\frac{| \alpha |}{3} \right ) \cdots \left (1+\frac{| \alpha|}{N-1} \right ) |x| ^{N-1} =K(nに関して定数)とおけます。$$
$$よって、|R_n(x)|<KC \left(\frac{ |x| }{r}\right)^{n-N-1}で、 \frac{ |x| }{r}<1 ですから、$$
$$\lim_{n\to \infty} \left(\frac{ |x| }{r}\right)^{n-N-1} =0, 従って \lim_{n\to \infty} |R_n(x)| =0 $$
よって、n→∞で剰余項が0に収束するので |x|<1の時 、x=0においてテイラー展開可能(つまり Mcl. 展開可能)です。【証明終り】
\((1+x)^{\alpha}\) の剰余項が|x|≧1の範囲では収束しない事
★尚、x≧1の時は剰余項が収束しない事については、少し遠回りですが、次のように考えます。
|x|<1 の時にマクローリン展開が可能であるわけですが、このように整級数の形で無限級数展開できた場合、じつは収束半径を計算する公式を使う事ができるのです。
$$公式:\sum_{n=0}^{\infty}a_nx^nの収束半径を\rho とすると、\frac{1}{\rho}=\lim_{n\to \infty}\left|\frac{a_n}{a_{n-1}}\right|$$
【ただし、公式を適用できる条件があり、この極限が収束するか+∞に発散する場合に限ります。】
その公式を使うと、収束半径は1であるという結果が出ます。 整級数は収束半径未満のxの範囲で収束します。従って、x≧1の範囲でMcl.展開できたとすると、その形の収束半径が1である事に矛盾してしまうので|x|≧1でn→∞において剰余項が0に収束する事はあり得ない、というわけです。
注意すべきは、であるからといって|x|<1で剰余項が0に収束する事が直ちに示されるか?というとそうではないという事です。 |x|<1で関数をMcl.展開の形の整級数で表せるかどうかは、面倒ですが例えば上記のような方法でその範囲で確かに剰余項が0に収束する事を証明する必要があるのです。
このように\((1+x)^{\alpha}\)の形の多項式に関するMcl.展開可能性の理論は、厳密に見ると意外に細かくて面倒ですが、これによって一般2項定理が成立する事が確かに分かります。
また、物理等でも平方根や分数の形を無限級数の形にして(多くの場合3次以降等の高次項は0とみなして)理論を分析する事がよくありますが、そこで使われるのがMcl.展開です。平方根は「1/2乗」、分数は「-1乗」でもあるので、そのような事ができるのです。