今回は、極限について、より数学的に考えた場合にはどのような定義になるのかといった事を紹介します。じつはこのページで語られる内容が、大学の学部での一般的な解析学・微積分学で最初に教えられるものです。そのため、今回の内容は数学科で教わるような「解析学の初歩」をかなり分かりやすく説明した内容にもなっています。その内容を見てみましょう。
解析学的な極限の厳密な定義は?
■ 数列の極限の定義とε-N論法 ■ 実数の性質 有理数にない性質は? ■ 有界性と上界 下界 上限 下限
数列の極限の定義とε-N論法
解析学での極限の理論は、数列の極限が初歩的で基本的内容となるので、まずそれを述べましょう。
\(\frac{1}{n},\frac{1}{n^2}\)といった数列は、限りなく0に近づきます。
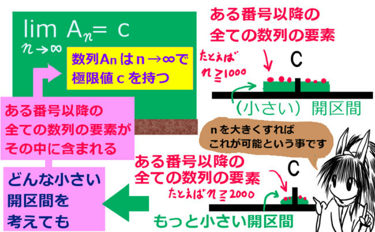
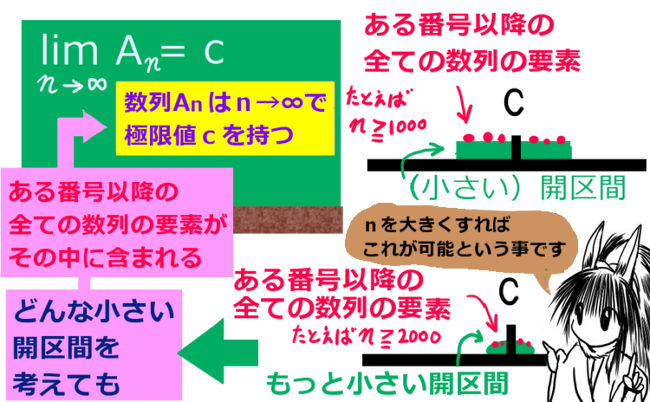
この事について、極限値である0を基準にして考えた時、0を含む任意の区間(普通、開区間を考えます)内にある番号以降の数列がおさまる事を意味するのです。
「任意の区間」とは、「任意の『小さな』区間」を想定しています。
例えば、( -0.001 , 0.001 ) のような開区間です。数列1/nであれば、n=1001以上であれば、全てこの小さな区間内に入るわけです。
数列の、ある番号以上の「全ての」要素を考える理由は、「振動」の可能性を除くためです。振動してしまう場合は、収束では無く発散の部類に区分します。
この時、別の ( -0.0001 , 0.0001 ) のような、さらに小さい開区間を考えると、n=10001 以上でなければ要件を満たしません。そのため、数学的には次のように考えます。
- まず、値cを含む開区間 U を考え、ある番号以上では全てそこに含まれるとする
- どんな小さな開区間 U を考えても、対応する番号 N が存在するとする(これを、「任意の開区間Uに対し、ある自然数Nが存在する」などと表現します)
- そのような条件を満たす時、数列はn→∞で「極限値cを持つ」と呼ぶ事にする(定義する)
$$\lim_{n\to \infty}A_n=c $$ $$\Leftrightarrow c を含む任意の開区間 U に対してn ≧ N_0 ならば A_n\in U となる自然数 N_0 が存在する$$
★ この小さな開区間の事を、「近傍」(英:neighborhood)とも言います。
日本語の場合、「どんな実数でも」という事を「任意の実数に対して」という、少々難しい言い回しで表現する習慣があります。これに対して、じつは英語の場合では、日常で使う言葉をそのまま使う習慣があります。
「任意の実数 R に対して」を英語で言うと、for all real numbers R となります。
every や each を使っても表現されます。for each real number R 等。意味するものは大体同じです。
多くの微積分学・解析学の教科書では、同じ内容を不等式で書く事も多いです。その場合、「任意の正の(小さい)実数」をギリシャ文字の「イプシロン」ε で表すのが通例です。
$$\lim_{n\to \infty}A_n=c $$ $$\Leftrightarrow 任意の正の実数\epsilon に対してn ≧ N_0 ならば |A_n – c| < \epsilon となる自然数 N_0 が存在する$$
★ これは、極限値と数列の差が「限りなく小さくなる」=「どんな小さい正の実数cよりも小さくできる」・・と、捉えているわけです。
この方法による定義を、慣習的に 「イプシロン・エヌ論法」と呼んだり、後述しますように関数の場合には別の正の実数デルタ δ を考える事から「イプシロン・デルタ論法」と呼んだりします。
これらの定義は、分かりにくい事で悪名高いものでもあります。(意味としては難しくないのですが。)
実際、物理などで関数等の極限を考える時は、これらの定義はあまり重要でない事も多いです。
例えば、1/n や 1/x などの数列や関数は、直感的に捉えても上記の定義を使っても結局「極限値は0」という結果は同じなのです。そのため、同じ結果を得るのであればよりシンプルな考え方をすべきだ・・とも、言えるわけです。
数学的に厳密に考える利点があるのは、収束するのか発散するのかすごく微妙で、直感的には判定しがたいという場合です。そのような場合は、物理や工学などでの応用よりも、純粋数学的な議論において多いと思われます。
実数の性質 有理数にない性質は?
次に、極限に関する基礎的な理論を下支えするものとして、実数が持つ性質が重要です。実数とは有理数に無理数を合わせたものですが、無理数とは「実数のうち有理数でないもの」・・などと説明されますから、これでは実数とは何なのか?という事の説明としては不足するものがあります。
結論を言うと、次の有理数の性質は、実数も共有するものです。
- +-÷× の四則演算などが定義できる(より正確には「体」(field) であるという事)
- 「順序構造」がある・・異なる2つの要素を選んだ時、p < q または p > q が必ず成立する。
★ これは、実数も備えている性質であるわけです。実数とは全ての有理数を含んだ集合ですから、有理数が持つ性質は実数も全て備えていなければならない、とも言えます。
では実数にしかない性質は何だろう?と考えると、次の「切断」(Schnitt これはドイツ語由来です)と呼ばれる、部分集合の分け方において成立する事が、じつは有理数と異なるのです。
「切断」とは、ごく簡単に言うと1箇所だけ境を決めて、1つの集合を2つの部分集合に分けるという操作です。例えば実数全体を「0以上」と「0未満」に分ける事は「切断」に該当します。(必ずしもその集合に属する「1点」で分けない場合も含みます。)
順序構造を持つ集合Mと、M のある要素 c について、次の条件を満たす部分集合AとBに分割する事を「Mのcにおける『切断』」と呼ぶ: $$①A\cup B=M\hspace{10pt}②A\cap B=\phi\hspace{10pt}③任意のa\in A,b\in Bに対してa<b $$
部分集合AとBの役割は入れ替えても同じです。
要するに、このような2つの部分集合を考えるという事を意味しています。
\(\mathbb{R}\)のcにおける切断によってできる部分集合AとBにおいては次の事が必ず成立する: $$「Aの最大値」と「Bの最小値」のどちらかだけが存在し$$ $$「Aの最大値 と B の最小値も両方存在しない」という事は起こらない$$
★ 尚、どんな集合の切断でも「A の最大値と B の最小値も両方する」という事は起こりません。
これを仮定すると、矛盾が生じるためです。
有理数の場合、じつは有理数全体における「切断」を考えた時には、切断で作った部分集合AとBについて「A の最大値 と B の最小値も両方しない」という事が起こります。
これを見るには、例えば \(q^2<2\) と \(q^2>2\) を満たす2つの部分集合に有理数を分けます。これはじつはきちんと「切断」に該当するのです。ところが \(q^2=2\) を満たす有理数は存在しませんから、これらの部分集合に最大値も最小値も存在しないという事です。
それに対して、これが実数の切断であれば \(r^2=2\) を満たす \(r=\sqrt{2}\) が存在しますからどちらかの部分集合に最大値か最小値が存在できるわけです。
有界性と上界、下界、上限、下限
さて、次に実数の中の部分集合(具体的には数列や関数)に対する、極限に関連する用語で重要なものを見ていきます。
これらも、意味としては簡単です。
ただし、記号などでごちゃごちゃ書かれると分かりにくいですから、意味を理解する事が重要です。
実数の部分集合Aとその要素 a について、 Aが「上に有界である」事と「下に有界である」事を次のように定義します。
- 上に有界である:
\(任意のa\in A について a < c となる実数 c が存在する\) - 下に有界である:
\(任意のa\in A について a > c となる実数 c が存在する\)
「上」「下」「有界」という語が入っていれば、多少の文章での使い方は変えてもよい習慣になっています。例えば「上に有界なので・・」のように使えます。
意味としては全く難しくなくて、例えば数列1/nは必ず0より大きいので「下に有界」です。また、nが自然数であれば最大値は1ですから「上にも有界」です。これが関数1/xでxが正の実数であれば、「下には有界」であるけれどx→0で無限大に発散するので「上には有界でない」事になります。
次に、上界と下界です。これらはそれぞれ、上に有界である集合、下に有界である集合について考えられます。要するに、数列や関数よりも「必ず大きくなる集合」と「必ず小さくなる」集合です。
実数の部分集合が上または下に有界である時、
集合「上界」と「下界」を次のように定義します。
- 上界:\(U={c|任意のa\in A について a ≦ c}\)
- 下界:\(V={c|任意のa\in A について a ≧ c}\)
【{x|・・・}は、「・・・を満たすxから成る集合」の意味】
上界は「じょうかい」、下界は「かかい」と読みます。UとかVの記号は、何でも構いません。
数列1/nは0より大きい事によって下に有界であると言えるわけですが、-1よりも必ず大きいので下に有界であると言ってもよいのです。
そのような、必ず1/nより小さくなる実数の集合が1/nの下界であり、「0以下の全ての実数」という集合を指すわけです。
定義の説明としては最後に、上限と下限を見てみましょう。これらも意味としては簡単で、それぞれ「上界の最小値」「下界の最大値」という意味で使います。
有界である実数の部分集合 A の上界 U と下界 V に対して、
上限(supremum)と下限(infimum)を次のように定義します。
- 上限:\(\sup A=\mathrm{min} U\)(Aの上界 U の最小値)
- 下限:\(\inf A=\mathrm{Max} V\)(Aの上界 V の最小値)
上界または下界の要素は無限個ありますが、特にそれぞれの最小値と最大値に注目するわけです。対象となる集合が数列であれば、$$\sup A_n,\inf A_n といった表記もなされます。$$
さてここで、上界が存在するなら上限は必ず存在し、下界が存在するなら下限は必ず存在するという事実があります。特に名前はついていない定理ですが、重要なので述べておきましょう。
有界である実数の部分集合 A に対して、 上界 U と下界 V に対して、
- A の上界Uが存在するならばAの上限:\(\sup A=\mathrm{min} U\)も存在する。
- A の下界Vが存在するならばAの下限:\(\sup A=\mathrm{Max} V\)も存在する。
上界または下界の要素は無限個ありますが、特にそれぞれの最小値と最大値に注目するわけです。
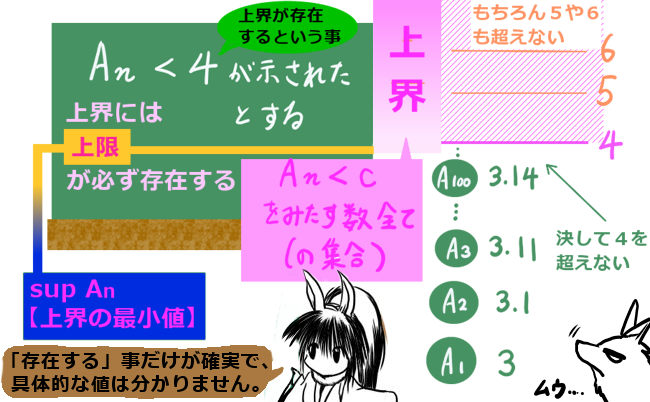
円周率や、自然対数の底 e はこの理屈によって、上限として「存在する」事が証明されます。
他方で、円周率が3.141・・である事や e = 2.718・・である事は、直接的に数列の値を計算したり、無限級数展開を利用したりして示す必要があります。
これは自明な事ではないので証明が一応必要です。実数の完備性を用いる事で確かに成立する事を示せます。参考までに、記しておきます。
証明:上界には最小値が存在し、下界には最大値が存在する
Aの上界Uと、実数のうちAの上界でない集合\(\bar{U}\)は実数全体の「切断」になっている事に注目します。
実数全体に対する切断なので、Uと\(\bar{U}\)のどちらか片方「だけ」に必ず最小値あるいは最大値が存在します。
しかし、上界の定義から、\(\bar{U}\) の任意の要素 c に対して、必ず c < a となるAの要素 a が存在します。【上界の定義の否定を考えるわけです。】
となると、そのような c と a の間には必ず別の実数が存在し、(例えば\(\frac{c+a}{2}\))、その実数は\(\bar{U}\) の要素です。これは、\(\bar{U}\) の任意の要素 \(c_1\) に対して、\(c_1<c_2\)となる別の要素 \(c_2\) が存在するという事なので、\(\bar{U}\) には最大値は存在しません。
よって、もうひとつのほうの「Uに最小値が存在する」事が真という事になるので、上界には必ず最小値・すなわち上限が存在します。【証明終り】
下界に対して下限が存在する事の証明も、全く同じ論法によります。
解析学の基本的な定理:有界な単調数列は収束列である
数列や関数が特定の極限において収束するのか発散するのかを調べて理論を形成する事が、解析学では行われます。その1つとして、「有界である単調数列は収束列である」という事実(「定理」)は重要ですので見ておきましょう。単調数列とは単調増加あるいは単調減少数列という事です。収束列とは、単純に「収束する数列」という意味です。この時、もちろん上に有界である数列が収束する条件(の1つ)は単調増加である事、という意味です。
円周率や自然対数の底といった重要な定数が極限値として存在する事の根拠は、この定理です。
■ 証明の流れと概要
■ 定理の証明:上限あるいは下限が極限値となる事を示す
■ 具体的な「有界な単調数列」にはどんなものがある?
証明の流れと概要
まず、証明の流れを見ておきましょう。有界には上に有界と下に有界である場合(あるいは両方)がありますから、それぞれの場合に分けます。
- 上に有界である単調増加数列
- 下に有界である単調減少数列
証明の方法は全く同じなので、片方だけ示せばもう片方も全く同じように証明できます。ここでは、上に有界な単調増加数列の場合を考えます。
- 数列が上に有界であるから、上限(最小の上界)が存在する事実を確認
- 上限を含む任意の(小さな)開区間\(U_{\epsilon}\)を考える
- 少なくとも1つ、数列の要素がその開区間内に含まれる事を示す
- 単調増加関数である条件を適用すると、数列の上限が極限値の定義を満たす事が分かるので、これが極限値であると判定。→ 証明完了
要するに、上に有界である場合は「上限」が必ず存在するわけですが、その上限が数列の極限値に(必ず)なる、という事です。その詳しい証明を次に見ましょう。これはそれほど難しい証明ではなく、事実関係や極限の定義を丁寧に整理すれば「確かにそうである」事が言えるというものです。
★ 尚、数列とは、厳密にはそれ自体は集合よりもむしろ関数として考えるべきもので、集合として考える時は「そのような関数の値からなる集合」を考える必要が本来はあります。そのような厳密な区分が重要である場合もあります。
しかし、それは表記として少々煩雑でもあるので、数列{\(A_n\)} における具体的な \(A_1, A_2 \) などをここでは「数列の要素」と記す事にします。
定理の証明:上限あるいは下限が極限値となる事を示す
まず、単調増加数列が上に有界である時、それがどんな数列であろうともn→∞で収束する事を証明しましょう。上に有界という条件ですから、まず無限大に発散はしない事は明らかですが、明確に「極限値」が存在するかどうかが曖昧なので明確にしようというわけです。
前述のように、上に有界であれば上限すなわち「上界の最小値」が必ず存在します。結論は、この上限が数列の極限値という事になります。
$$\sup A_n=c とおくと任意の自然数nに対してA_n<c$$
ここで、このページの最初のほうでも述べた、極限値の定義を考えましょう。この場合は、不等式も使ったほうが簡単です。任意の小さい正の実数εを考え、区間 \(U_\epsilon =( c -\epsilon ,\hspace{5pt}c ] \)を考えます。
【※c -ε 側は開区間、c側は閉区間という事です。(c -ε ,c + ε) を考えても別に構いません。ここでの場合は単純に、cより大きい範囲は考える必要はないというだけです。】
この時、区間 \(U_\epsilon =( c -\epsilon ,c ] \) 内に数列の要素が含まれないという事はあり得ないのです。なぜなら、もしそのような事が起こるなら任意の自然数nに対して \(A_n ≦ c -\epsilon\) という事になり\(c -\epsilon\)も上界の1つという事になりますが、cが「最小の」上界なのですからそれはあり得ない、という事です。
【ここの部分に関しては、そのように仮定すると矛盾するから、という背理法の論法でも同じです。】
すると、少なくともある1つのn=Nについて、 \(A_N\in U_\epsilon( c -\epsilon ,c ] \) という事は言えるわけです。
ここで、\(A_n\) は単調増加数列という条件であれば、
任意のn≧Nを満たす自然数について、 \(A_n\in U_\epsilon( c -\epsilon ,c ] \) という事になります。
【c は上界の1つですから、nをどれだけ大きくしてもcを超える事はありません。】
さて、これで一体何が言えたのかと言うと、
「cは\(A_n\) 極限値の定義の条件としてぴったり当てはまる」事が言えたのです。
つまり \(A_n\) はn→∞で極限値cを持つ事が証明された、という事になるのです。
【証明終り】
このように、定義や事実関係を丁寧に当てはめていく事でこの定理は証明されます。下に有界である単調減少数列も、全く同様に下限を極限値として持つ事を証明できます。
具体的な「有界な単調数列」にはどんなものがある?
では、有界な単調数列とは具体的にはどんなものがあるでしょう。抽象的には表せるけれども具体例が全く見つからない・・というのでは、純粋数学的にもあまり有意義とは言えません。具体的には、1/nなどのごく簡単な数列は下に有界で単調減少である数列の1つです。この他にも、有界な単調数列というのは少し考えれば具体的にたくさん見つかるのです。
問題はむしろ、特定の数列が「有界な単調数列」かどうかの判定が分かりにくい場合でしょう。
$$例えば、\left(1+\frac{1}{n}\right)^n \hspace{5pt}や \hspace{5pt} \sum_{j=1}^n\frac{1}{n}-\ln n \hspace{5pt} などの数列です。$$
これらは、見た目では有界なのかも単調数列なのかも、ちょっと分かりにくいですね。結論を言うとこれらはどちらも有界な単調数列であり、それぞれ極限値を持ち e(自然対数の底、ネピア定数), γ(ガンマ、オイラー定数) で表される事が普通です。
円周率も、特定の数列の極限値です。この場合、円に内接および外接する正n角形の周の長さを数列として表した時に有界な単調数列になります。半径が1の円の円周の長さが円周率の2倍になります。【極限値が存在する事が分かれば定数倍に関しては調整できるので、円周率に関してはそのように定義しておくという事です。】
実関数の場合の極限と連続の定義
最後に、変数が実数である一般の関数(実関数)の場合の極限の定義なども整理しておきます。数列の場合は、言わば「変数が自然数」であるわけです。変数が実数になる事で、極限の定義なども1つ2つ文言が増えますが、基本的な考え方は同じです。
■ 関数の場合の極限の定義: ε-δ論法 ■ 関数が連続であることの定義 ■ 微分と関数の連続性の関係
関数の場合の極限の定義: ε-δ論法
まず、極限値となる値を含む任意の開区間を考える点は、数列の時と全く同じです。異なるところは、数列の場合において「n≧Nとなる任意のnについて」の箇所で、これを関数の場合にはどうするかという事が、問題になります。これに対しては、変数を無限大にする時と、特定の値に近づける時とで2つ定義を設けます。(本質的な意味は同じです。)
- 変数を無限大にする時の関数の極限:\(\lim_{x\to \infty}f(x)\)
- 変数を有限の値に近づける時の関数の極限:\(\lim_{x\to a}f(x)\)
数列の場合はn=1が変数の最小値ですが、関数の場合は x → 0 の時の極限なども考える事ができる、という事です。
この場合は数列の極限と大体同じ考え方です。ある値を含む任意の(小さな)開区間に、ある値以上の任意の変数に対する関数の値が全て含まれる事を定義にします。 $$\lim_{x\to \infty}f(x)=c$$ $$\Leftrightarrow c を含む任意の開区間 U に対して、x ≧\delta ならばf(x)\in U となる実数\delta が存在する$$ この場合、無限大∞は正の方向の無限大であり、それを明確にする場合は +∞ とも書きます。実関数の場合、変数をマイナスのほうの無限大にした時の極限も考えます。考え方は同じです。 $$\lim_{x\to -\infty}f(x)=c$$ $$\Leftrightarrow c を含む任意の開区間 U に対して、x ≦\delta ならばf(x)\in U となる実数\delta が存在する$$ 数列の時と同様、「任意の開区間」の部分を(小さな)正の実数\(\epsilon\) を用いた不等式を使っても同じ事です。 $$\lim_{x\to a}f(x)=c$$ $$\Leftrightarrow 任意の正の実数\epsilon に対しx ≧\delta ならば|f(x)-c|<\epsilon となる実数\delta が存在する$$
特定の有限の値に変数を近づける場合、対象が変な関数だと変数を「a より大きい側から近づけた時」と「 a より小さい側から近づけた時」に、極限値が異なる場合があります。そのような事があるので、解析学で厳密な考察をする場合は両者の極限を区別し、両者が一致する場合にその極限での「極限値」が存在すると呼ぶ事にしています。
尚、もし「右極限」と「左極限」の値が異なる場合には上記の という条件は満たされないのです。
$$「c を含む任意の開区間 U に対して、x \in V_{\delta} ならば f(x)\in U となる a を含む開区間V_{\delta} が『存在できない』」$$
それは、a を含む開区間の中で a よりも「大きい側」と「小さい側」とで、関数が別々の \(c_1 と c_2\) という値を含む開区間に含まれる事になってしまうからです。
参考までに、右極限と左極限が存在するけれども異なる値になる場合は上記の関数の極限の定義に当てはまらず、「極限値が存在しない」判定になる事を、一応式でも記しておきましょう。
2つの開区間\(U_1とU_2\)が共通部分を持たないように区間の幅を小さく取った時、a を含む開区間をどのようにとっても\(x\in U_1\) になる部分と\(x\notin U_1\) となる部分に分かれてしまいます。
- \(x\in U_1 になる部分:[a, a+\delta_1)\)
- \(x\notin U_1 となる部分:(a-\delta_1,a]\)
関数が連続であることの定義
関数が連続である事の定義も、極限の定義の延長線上にあります。三角関数や指数関数などの初等関数は連続関数です。
連続性の厳密な数学的定義は、物理などへの数学の応用ではそれほど重要ではないと思います。ただし、数学の解析学・微積分学の中では重要な基礎理論になりますので、考え方だけは見ておきましょう。
関数の定義域内の実数(の点) a において関数が連続であるとは、次の条件を満たす事を言います:
$$f(a)=\lim_{x\to a}f(x)$$
これは、1次関数、2次関数、三角関数、指数関数・・などの初等関数を単独で考える場合は「当然」の事なので、それほど重要とは言えないかもしれません。
数学の理論上、多くの場合に問題となるのは、次のような変な関数です:
- 例①:「\(x=0 のときf(x)=0,x≠0 の時 f(x)=\sqrt{|x|}\sin \frac{1}{x}\)」という f(x)
- 例②:「\(x=0 のときf(x)=0,x≠0 の時 f(x)=\sin \frac{1}{x}\)」という f(x)
このように、初等関数での感覚で言う「つながっている」事が必ずしも不明確でない関数を考える場合には数学的な定義を決めておく事は重要にもなるのです。(こういった関数が物理などへの応用で使えるかどうかは、また別の問題になります。)
関数が連続であるかどうかという事は、関数自体の性質を探求する事以外に、微分の理論においても重要な位置付けにあります。ある点で微分可能であるかどうかと関数の連続性が深く関わるからです。
参考:定義域の完備性、関数の連続性と一様連続性
普通は、関数の定義域(変数が取り得る値の範囲)を、実数全体であるとか、特定の閉区間や開区間を想定します。このような定義域は、実数全体の性質と同じく、「完備性」を持っていると呼びます。上記の説明においても、それを前提にしています。
他方で、あくまで理論上の話ですが、定義域として「無理数全体」などという無茶苦茶なものを考える事も数学上は可能なのです。これは、数直線上で言うとボコボコの「穴だらけ」の定義域です。
しかし、そのような滅茶苦茶な定義域上の関数でも、適当な関数を用意すれば上記の連続性の定義に当てはめて「『定義域上の』任意の点で連続である」という判定になってしまう事が知られています。
例えば、次のような簡単な関数を考えればじつはじゅうぶんです。
- x>0の時 f(x)=1
- x<0の時 f(x)=0
- 定義域は、無理数全体
事の本質は、じつのところ「本来は不連続点と言うべき点を、定義域から除外さえしてしまえば不連続な点はない事になる」・・というところにあります。
より簡単な例では、1/xという関数でx=0で不連続「のはず」ですが、そもそもx=0を定義域から除外しておけば「不連続点はない」という、おかしな事になるといったものです。
これを解消するためには、「一様連続」というものを定義します。一様連続性の定義は次のようなものです。
$$任意の正の実数\epsilon に対し、定義域内で|x-y|<\delta を満たす『任意の2点』x,y に対して$$
$$|f(x)-f(y)|<\epsilon となるような、正の実数\delta が存在する。$$
この一様連続性の考え方は、微積分の理論でも使用する事があります。
微分と関数の連続性の関係
さて、微分や積分も極限の一種です。ここでは、微分について考察してみましょう。初等関数の微分を考える時は、前述の厳密な極限の定義を考える事よりも、上手な式変形をして明らかに極限値が分かるようにする事のほうが重要である場合が多いです。
他方で、変な関数も含めた一般の関数を数学的に考える場合は、どのような場合に微分が可能で、どのような場合に微分が不可能なのか?といった事を明確にしておくことも、理論的な位置付けとして重要なのです。
結論を言うと、定義域内での特定の点での微分可能性と連続性については、次の関係があります:
- ある点で微分可能ならば、連続でもある
- ある点で連続であっても、微分不可能な場合がある
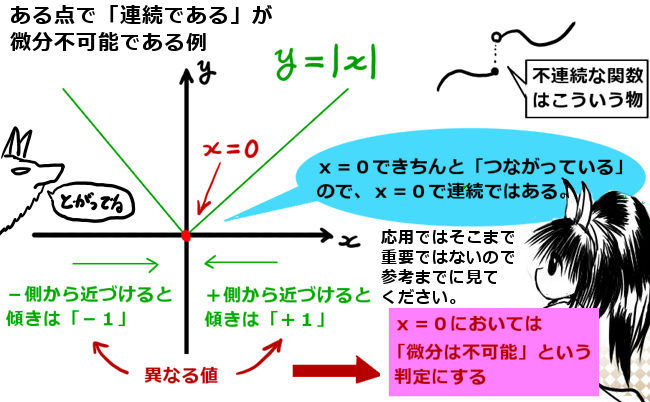
「連続であっても、微分不可能な場合」とはどういう事かと言いますと、一番簡単な例は f(x) = |x| という関数です。これは、グラフで見るとx=0の点で「尖っている」関数です。このように、ある点で必ずしも「なめらかでない」場合でも、つながっていれば「連続である」という判定になります。(もちろん厳密には上記の定義に当てはまるか、式を使って判定します。)
しかし、 f(x) = |x| のx=0における状況を見ると、微分係数とは「傾き」であったはずですが、x=0では傾き+1と-1のどちらを採用するのかという話になります。このような場合、その点では「微分不可能」という判定をするのです。そのため、「関数 f(x) = |x| はx=0 で連続であるが微分不可能である」という事です。尚、「x≠0の任意の点で、 関数 f(x) = |x| は『連続であり微分も可能』 」です。
全く同じ事ではないので注意が必要な事もあります。
前述の極限と連続性の定義から考えると、 f(x) = |x| の微分係数はx=0 において、
$$右極限\lim_{h\to +0}\frac{f(x+h)-f(x)}{h}と左極限 \lim_{h\to -0}\frac{f(x+h)-f(x)}{h} は共に存在するが値は異なる$$
というパターンに該当します。
\(右極限\lim_{h\to +0}\frac{f(x+h)-f(x)}{h}=+1, 左極限 \lim_{h\to -0}\frac{f(x+h)-f(x)}{h} =-1\) で、異なる値というわけです。
そのため、極限値として厳密に定義に当てはめた場合、極限値としての微分係数も存在しない、という判定になります。
$$ f(x) = |x| の時、極限値としてのx=0での微分係数\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}は存在しない。 $$
つまり、直感的に考えて「傾きが一意的に定まらない」という事と、数学的に考えて極限値が存在しないという判定になる事は、一応調和しているわけです。
このような場合以外に、関数自体が無限大に発散する点においても、微分係数も無限大に発散し、微分不可能という判定にします。そのような点では、関数は「不連続かつ微分も不可能」という事になります。
尚、一応これは「微分可能ならば連続である」という事実の対偶命題を考える事により「不連続ならば微分不可能」と言う事もできます。不連続点では、どのような場合でも微分不可能というわけです。
今回お話した内容は、上記でも少し触れましたように、物理等への応用よりも、純粋数学的な内容の基礎事項という側面が強いです。ただし、有界な単調数列は収束列であるといった事は、円周率や自然対数の底といった重要な定数の極限値としての存在の根拠でもあり、これらの定数は物理や工学でも使用しますから、大まかな事は知っておいてよいのではないかと思います。
参考文献・参考資料

微分積分学〈1〉1変数の微分積分