平方根の考え方と基本計算について説明します。
英:平方根 square root
定義と記号の書き方
まずは定義と記号からです。
「2乗するとnになる数」の事をnの平方根と言います。
n>0の時、平方根はプラスものとマイナスのものの2つがあります。
この時、「nの平方根でプラス符号のもの」を特に「ルートn」と呼んで次の記号で書きます。
【root:植物の「根」。数学では「こん」と呼ぶ】$$\sqrt{n}\hspace{20pt}\sqrt{2}\hspace{20pt}\sqrt{3}$$
「2乗すると2になる数」であれば「2の平方根」であり、
プラス符号のものを \(\sqrt{2}\) と書き「ルート2」と読みます。
これらを使って、マイナス符号の平方根は次のように表します。
$$-\sqrt{n}\hspace{20pt}-\sqrt{2}\hspace{20pt}-\sqrt{3}$$
マイナス1の2乗はプラス1なので、
これらを2乗しても確かにn、2、3といった数になります。
「平方」とは要するに「2乗」の事で、「平方根」の事を「2乗根」とも言います。
22=2×2=4、32=3×3=9の「2乗」の事です。
長さの単位で、1平方センチメートル1cm2というのがありますね。
あれに使われている「平方」です。

このとき、文字式を組み合わせた式の「平方根」を考える事もできます。
(これは一部、中学校の数学でも扱います。)$$\sqrt{x^2+y^2}\hspace{20pt}\sqrt{b^2-4ac}\hspace{20pt}\sqrt{1-\frac{v^2}{c^2}}$$尚、これらの例は1つめが図形問題で三平方の定理を使う時に出てくるような式、
2番目は2次方程式の解の公式に出てくる項、
3番目は相対性理論で重要になる量の1つです。(cは光の速さ、vは物体の速さ)
平方根の考え方は中学数学だけでなく、数学全般や数理科学で普通に使うものですので基礎事項をしっかり理解しておくと後々便利です。
これらの基本的な考え方は\(\sqrt{2}\) や \(\sqrt{3}\)と同じで、2乗すると「平方根が消える」ような計算になります。$$\left(\sqrt{x+y}\right)^2=x+y\hspace{20pt}\left(\sqrt{b^2-4ac}\right)^2=b^2-4ac\hspace{20pt}\left(\sqrt{1-\frac{v^2}{c^2}}\right)^2=1-\frac{v^2}{c^2}$$
平方根の整数倍、例えば2倍、3倍などは \(2\sqrt{2}\) , \(3\sqrt{2}\) のように書きます。
文字式のaの2倍や3倍を2a、3aと書く感覚です。
整数倍の時は次のようにします。
$$2×\sqrt{2}\hspace{3pt}=\hspace{3pt}2\sqrt{2}\hspace{15pt}-3×\sqrt{2}\hspace{3pt}=\hspace{3pt}-3\sqrt{2}のように書きます。$$
一般的には、平方根を分数倍した時には分子に平方根を一緒に書く事が多いです。
$$\frac{1}{3}×\sqrt{2}=\frac{\sqrt{2}}{3}\hspace{15pt}\frac{2}{3}×\sqrt{2}=\frac{2\sqrt{2}}{3}$$
文字式と平方根を組み合わせる時には、2a、3bと書く感覚で平方根を文字式の前に書きます。
そこにさらに整数倍がある時は、整数・平方根・文字式の順番にする事が多いです。
$$a×\sqrt{2}\hspace{3pt}=\hspace{3pt}\sqrt{2}a\hspace{15pt}2b×\sqrt{2}=2\sqrt{2}b$$
負の数に対しても平方根を考える事ができて、例えば-2の平方根は次の2つです。 $$\sqrt{-2}\hspace{3pt}=\hspace{3pt}i\sqrt{2}\hspace{20pt}-\sqrt{-2}\hspace{3pt}=\hspace{3pt}-i\sqrt{2}$$ これらは複素数というものに属します。実数の範囲では、2乗して負の数になる数は存在しません。
小数で表すとどのような大きさ?
「2乗すると2になる数」である \(\sqrt{2}\) とは具体的にはどのような大きさの数でしょう?
\(\sqrt{2}\) の大きさは小数で表すと約1.4142135・・・になります。
この小数点は無限に循環しない形で続き、\(\sqrt{2}\) は無理数になります。
てきとうなところで小数点を四捨五入したもの、例えば「1.414」として2乗してみると
1.414 × 1.414=1.999396 であり確かに2に近い数になります。
いくつか例を挙げてみると次のようになります。
- \(\sqrt{2}\)=1.4142135・・・
- \(\sqrt{3}\)=1.7320508・・・
- \(\sqrt{4}\)=2
- \(\sqrt{5}\)=2.2360679・・・
- \(\sqrt{6}\)=2.4494897・・・
- \(\sqrt{7}\)=2.6457513・・・
- \(\sqrt{8}\)=2.8284271・・・
- \(\sqrt{9}\)=3
- \(\sqrt{10}\)=3.162276・・・
これらのうち、22=2×2=4、32=3×3=9ですから、
4の平方根と9の平方根を考えた時にはぴったりと整数の値になります。
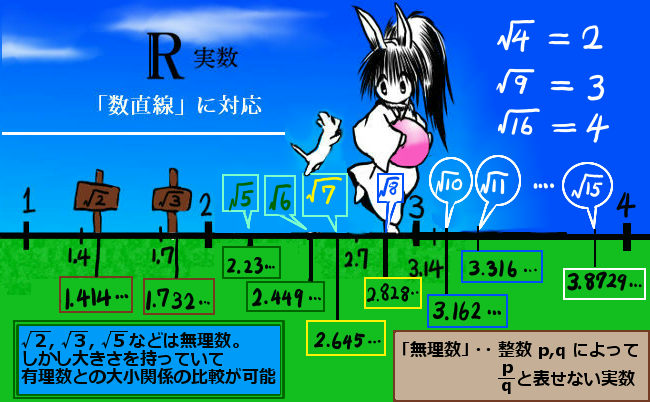
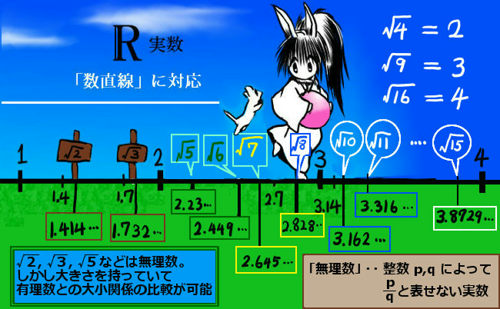
数直線上に有理数と合わせて大小関係を比べる事ができます。
これら平方根の小数の値は、\(\sqrt{2}\) や \(\sqrt{3}\) に関しては「1.414」「1.732」といった数値を覚えておくと便利な事もありますが、他のものはそれほど覚える必要はありません。
(ましてや、延々と続く小数を覚える必要はありません。)
それよりも重要なのは、平方根の値がどれくらいの大きさなのかを見積もる方法です。
例えば \(\sqrt{7}\) の大きさを知りたい時に「2以上3以下」といった事を知るのはじつは簡単で、
22<7<32という不等式によってその事を知れるのです。
もちろんこれは4<7<9という事です。
この不等式の各値の平方根(のプラスの値)を考えると2<\(\sqrt{7}\)<3となるので、
\(\sqrt{7}\) を小数で表した時の1以上の部分の値は2になると判定できるというわけです。
(実際の値は\(\sqrt{7}\)=2.6457513・・・)
そう考えると、\(\sqrt{5}\), \(\sqrt{6}\), \(\sqrt{7}\), \(\sqrt{8}\) の小数での値がいずれも 2.23・・などの、
「2より大きく3より小さい」値になるのは偶然ではなく必然という事になります。
5、6、7、8はいずれも4より大きく9より小さいからです。
この考え方は、何かてきとうな自然数の平方根に対して一般的に適用できます。
\(\sqrt{17}\) の大きさを見積もる時には
16<17<25、つまり42<17<52ですから
4<\(\sqrt{17}\)<5といった感じになります。(実際の値は\(\sqrt{17}\)=4.1231・・)
また、てきとうな\(\sqrt{151}\) といった数の大きさを見積もる時には
144<151<169、つまり122<151<132により、12<\(\sqrt{151}\)<13なので
\(\sqrt{151}\)=12.・・・・といった数になる事が分かります。(実際は12.2882・・)
この不等式の作り方・使い方に関しては高校入試でも問われる可能性はあります。
平方根に関する計算・公式
\(\sqrt{2}\) と \(\sqrt{8}\) の小数での値を比較すると、じつはちょうど2倍の関係になっています。
- \(\sqrt{2}\)=1.4142135・・・
- \(\sqrt{8}\)=2.8284271・・・=2×1.4142135・・・=\(2\sqrt{2}\)
これは偶然ではなく、8=22×2という関係があるのでそうなるのです。
\(2\sqrt{2}\) を2乗すると、確かに22×2=8になります。
一般的に、平方根の中に「何かの数の2乗」がある場合にこのような計算ができます。
いくつか具体例を挙げると次のような感じです。
- \(\sqrt{8}\) = \(2\sqrt{2}\)
- \(\sqrt{12}\) = \(2\sqrt{3}\)
- \(\sqrt{18}\) = \(3\sqrt{2}\)
- \(\sqrt{24}\) = \(2\sqrt{6}\)
- \(\sqrt{27}\) = \(3\sqrt{3}\)
- \(\sqrt{32}\) = \(4\sqrt{2}\)
- \(\sqrt{4x}\) = \(2\sqrt{x}\)
掛け算に慣れていないと少し分かりにくいかもしれませんが、
例えば32なら32=16×2=42×2のように考えるのです。それで\(\sqrt{32}\) = \(4\sqrt{2}\)になります。
(※入試対策としては、これを頭の中でできるようにするのが望ましいです。)

次に、「分母の有理化」という計算も重要です。
これは、分母に平方根がある場合には、分子と分母の両方にその平方根を掛ける事で
「分母を有理数にできる」という計算です。
1つめの式は、\(a=\sqrt{a}×\sqrt{a}\) を式変形して考えても同じです。
2つめの式は(a+b)(a-b)=a2-b2の関係を使っています。
同じ関係を使って、分母が平方根の差の場合には次のようにできます。$$\frac{1}{\sqrt{a}-\sqrt{b}}=\frac{\sqrt{a}+\sqrt{b}}{(\sqrt{a}-\sqrt{b})(\sqrt{a}+\sqrt{b})}=\frac{\sqrt{a}+\sqrt{b}}{a-b}$$
具体例では、例えば次のようになります。
$$\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}\hspace{20pt}\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\hspace{20pt}\frac{1}{\sqrt{1-x^2}}=\frac{\sqrt{1-x^2}}{1-x^2}$$
$$\frac{1}{\sqrt{3}+\sqrt{2}}=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}=\frac{\sqrt{3}-\sqrt{2}}{3-2}=\frac{\sqrt{3}-\sqrt{2}}{1}=\sqrt{3}-\sqrt{2}$$
$$\frac{1}{\sqrt{2}-1}=\frac{\sqrt{2}+1}{(\sqrt{2}-1)(\sqrt{2}+1)}=\frac{\sqrt{2}+1}{2-1}=\frac{\sqrt{2}+1}{1}=\sqrt{2}+1$$
この具体例のように「分母の有理化」を行う事で分母が1になり実質的に「分母が消える」場合もあります。
慣れてくると、途中の計算は暗算でできるようにもなると思います。
平方根同士の掛け算・割り算と足し算・引き算については次のような規則が成立します。
- 掛け算と割り算:
平方根の中身同士の掛け算・割り算をして計算で可能。$$\sqrt{a}×\sqrt{b}=\sqrt{ab}\hspace{15pt}\frac{\sqrt{b}}{\sqrt{a}}=\sqrt{\frac{b}{a}}$$ - 足し算と引き算:
基本的に同じ数の平方根同士で足し算・引き算を行い、そこからさらに計算したいなら小数で近似して数値的に加え合わせるなどする。 $$a\sqrt{c}+b\sqrt{c}=(a+b)\sqrt{c}\hspace{15pt}a\sqrt{c}-b\sqrt{c}=(a-b)\sqrt{c}$$ $$\sqrt{2}+\sqrt{3}のような式は、このままだとこれ以上計算できない。$$ $$(小数に近似すれば\sqrt{2}+\sqrt{3}≒1.414+1.732=3.146のようにできる)$$
平方根の掛け算については、(\(\sqrt{a}×\sqrt{b}\))2=\(\sqrt{a}×\sqrt{a}×\sqrt{b}×\sqrt{b}=ab\) なので、
\(\sqrt{a}×\sqrt{b}=\sqrt{ab}\) としてよいという事です。
割り算のほうについては「分母の有理化」もできますが、分子と分母の両方に単独の平方根がある場合には先に割り算をして平方根をとる事も可能である、という意味です。
$$\sqrt{2}×\sqrt{3}=\sqrt{2×3}=\sqrt{6}\hspace{15pt}\frac{\sqrt{6}}{\sqrt{3}}=\sqrt{\frac{6}{3}}=\sqrt{2}$$
分母と分子にある平方根が単独ではなく和や差の形になっている場合には、項を分ける・分母の有理化をするなどの計算が必要になります。
$$\frac{2\sqrt{2}+\sqrt{6}}{\sqrt{2}}=\frac{2\sqrt{2}}{\sqrt{2}}+\frac{\sqrt{6}}{\sqrt{2}}=2+\sqrt{3}$$
$$\frac{\sqrt{6}}{\sqrt{3}-\sqrt{2}}=\frac{\sqrt{6}(\sqrt{3}+\sqrt{2})}{(\sqrt{3}-\sqrt{2})(\sqrt{3}+\sqrt{2})}=\sqrt{6}(\sqrt{3}+\sqrt{2})=\sqrt{18}+\sqrt{12}=3\sqrt{2}+2\sqrt{3}$$
平方根の足し算や引き算は、基本的には文字式の足し算引き算のように考えるという事です。
例えば、文字式の場合には 2a+3a+b=5a+bのようにして、aとbの具体的な値が分からない限りはそこで計算はストップしますが、それと同じように考えるという事です。$$2\sqrt{2}+3\sqrt{2}+\sqrt{3}=5\sqrt{2}+\sqrt{3}【この先は平方根を含んだままの形では計算しない】$$
各平方根を有限の小数に近似する(つまり有理数に近似する)のであれば、さらに計算をする事が可能です。