角運動量の数学

物理学で考える「角運動量」は回転運動を表す物理量です。外積ベクトルを使って表します。

◆関連：ベクトルの基本事項と内積

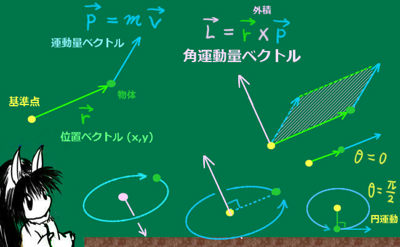
角運動量ベクトル

角運動量を外積ベクトルで表す事には幾つかの意味があります。

まず、回転の向きに関しては時計回り（順方向）と反時計回り（逆方向）という事もありますが、回転している「面」の事も含みます。例えば、空間内にｘｙｚの直交座標を考えた時に、同じ速さで同じの形の軌道を描いて回転している場合であっても、「ｘｙ平面での回転」「ｙｚ平面での回転」は当然「異なる運動」であると言えます。

そこで外積ベクトルの向きは、回転面の「軸」の向きに相当する方向を表す事になります。物体の運動方向が基準点から見て時計回り方向なのか、それとも反時計回り方向なのかも外積ベクトルの向きで表す事ができるわけです。（外積ベクトルの符号が反転すると運動量ベクトルの符号が反転し、全く反対の方向への運動を表す事になります。）

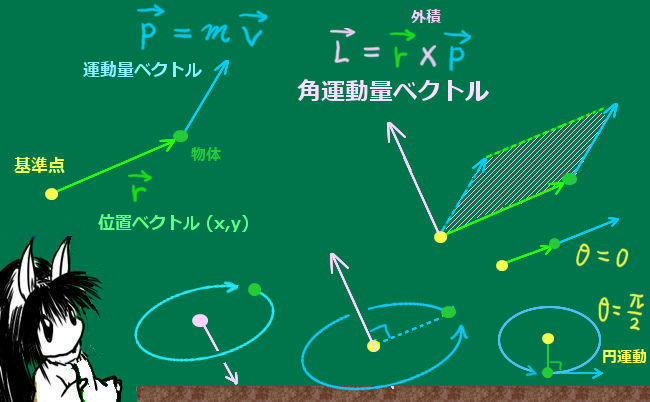
また、ある点を基準として同じ角速度で回転をしていても、その点の近くを回転している時と遠くを回転している時とでは、物体の速度は異なります。
「物体の位置ベクトル」\(\overrightarrow{r}\) は、回転の中心からの「距離」も情報として含むので角運動量ベクトルを構成する要素として使わます。（この事は「力の能率（モーメント）」と関係します。）

外積ベクトルで表されているという事は、２つのベクトルが平行である場合（成す角度が０または \(\pi\)である場合）には値が０である事になります。これは、物体の運動がある点から直線状に遠ざかっていく、あるいは直線状に近寄ってくるような場合であり、「回転」の様子がない事を表しています。

力の能率（モーメント）

力の能率（あるいは「力のモーメント）」moment of force）は角運動量ベクトルの時間微分として表されます。ベクトルに対する微分は、具体的には成分に対する微分として定義されます。

ここで角運動量ベクトルの定義通りの式に時間微分をすると考えると、外積ベクトルに対する微分をするいう事になりますが、これは通常の積の形に対する微分公式と同じ形が成立します。【証明は外積の成分表示を使うと比較的簡単です。】

すなわち、次式のように書けます。

$$\frac{d}{dt}\overrightarrow{L}=\frac{d}{dt}\left(\overrightarrow{r}×\overrightarrow{p}\right)=\frac{d\overrightarrow{r}}{dt}×\overrightarrow{p}+\overrightarrow{r}×\frac{d\overrightarrow{p}}{dt}$$

【ここで、位置ベクトルの時間微分は速度ベクトル\(\overrightarrow{v}\)である事に注意します。】

$$=\overrightarrow{v}×\overrightarrow{p}+\overrightarrow{r}×\frac{d\overrightarrow{p}}{dt}=m\left(\overrightarrow{v}×\overrightarrow{v}\right)+\overrightarrow{r}×\frac{d\overrightarrow{p}}{dt}=\overrightarrow{r}×\frac{d\overrightarrow{p}}{dt}$$

【最初のｔで微分した後の第１項は０になり、第２項だけが残るという事です。】

ところで、運動量ベクトルの時間微分とは何であったかというと「力ベクトル」\(\overrightarrow{F}\)であったわけです。（それが運動方程式が表現している事そのものです。）

という事は、角運動量ベクトルの時間微分は結局「位置ベクトル」と「力ベクトル」との外積という事になるわけです。

$$\frac{d}{dt}\overrightarrow{L}=\overrightarrow{r}×\overrightarrow{F}$$

この外積ベクトルの事を、「力の能率」あるいは「力のモーメント」と呼びます。

力の能率は、意味としては「大きさを持つ物体に力を働かせる時、ある支点から距離が離れているほど回転させる効果は大きい」というものですが、より詳しくは角運動量ベクトルの時間変化という事になるわけです。

角運動量の保存則

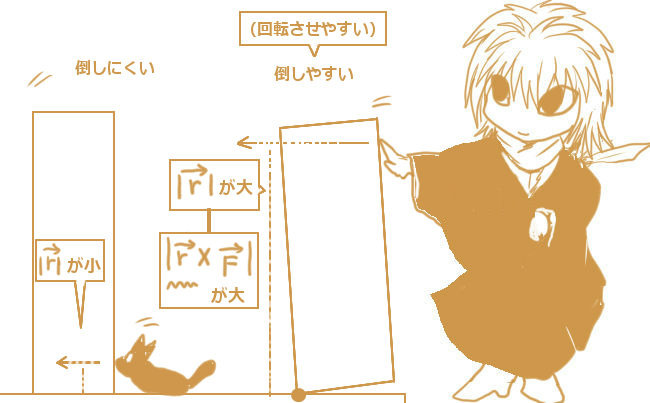
物体に働く力が「中心力」で、原点を中心にとった時には角運動量は保存量となります（角運動量保存則）。

この時には、角運動量ベクトルがどちらに向いているかはその時々によって異なりますが、
「力」の向き――つまり「運動量ベクトルの時間微分」の向きは、常に中心を向いている事を意味します。

従って、角運動量ベクトルが具体的にどう表されるかはその時々により異なりますが、
「力の能率は中心力のもとでは常にゼロベクトルである」と言えるわけです。

$$中心力が物体に働く時：\overrightarrow{r}×\overrightarrow{F}=0【ゼロベクトル。\overrightarrow{F}=C\overrightarrow{r}と書けるから。】$$

ところで、力の能率は角運動量ベクトルの時間微分であったわけですから、中心力のもとではそれが０になる事を意味します。

$$\frac{d}{dt}\overrightarrow{L}=\overrightarrow{r}×\overrightarrow{F}=0$$

時間微分が０であるという事は、「時間によって変化しない」事を意味します。（実際、ベクトルの各々の成分に対して、その形の微分方程式の解は時間に関して「定数」という事になります。「時間に依存しない」形となるわけです。）

$$\frac{d}{dt}\overrightarrow{L}=0\Leftrightarrow \overrightarrow{L}は定ベクトル（時間に依存しない。「保存」する）$$

この事を、「中心力のもとで角運動量は保存する」と表現します。
その事を、力学では角運動量保存則とも言います。

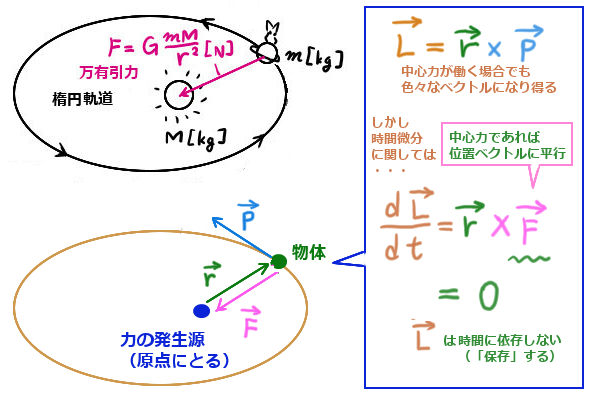
中心力のもとで軌道が円ではなく楕円のようになる場合にでもこの角運動量保存則は成立するので、中心力の発生源に近い場所では物体の運動量（および速さ）が大きくなり、発生源から離れているほど物体の運動量（および速さ）は小さくなる事を表しています。

剛体の角運動量

さて、では大きさを持った立体的な球とか円盤とか（変形しない事を仮定した場合に剛体と呼びます）が、
中心に立てた軸周りに「自転」している形式の回転の場合にはどうなるでしょうか。

この場合には、微小な体積領域で通常の角運動量を考えて、質量を位置の関数としての「密度」で表し、それに体積要素を乗じる事で表現します。それを領域全体で積分する事で「全角運動量」を計算するという形の理論になっています。

$$微小領域の質量：m=\rho dv【mと\rhoは\overrightarrow{r}の関数】$$

$$微小領域の角運動量ベクトル：\overrightarrow{r}×(\rho dv\overrightarrow{v})=\rho(\overrightarrow{r}×\overrightarrow{v}) dv$$

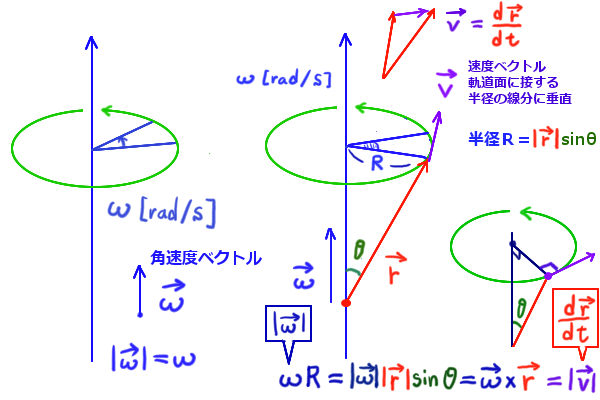
ここでは自転的な運動、つまり回転軸の方向が不変である場合を考えます。
その場合は、速度ベクトル\(\overrightarrow{v}\)は「角速度ベクトル」\(\overrightarrow{\omega}\)と位置ベクトル\(\overrightarrow{r}\)の外積として表せるという公式を使えるので、角運動量ベクトルの式を変形できます。

$$公式：\overrightarrow{v}=\frac{d\overrightarrow{r}}{dt}=\overrightarrow{\omega}×\overrightarrow{r}を使えるので、$$

$$\rho(\overrightarrow{r}×\overrightarrow{v}) dv=\rho\left(\overrightarrow{r}×(\overrightarrow{\omega}×\overrightarrow{r})\right) dv$$

この関係式は、より一般的に角速度ベクトルが定ベクトルではなく時間的に変化する関数になっている場合でも成立します。

外積ベクトルの公式（「ベクトル三重積」）を使うと、もう少し計算を進められます。

$$\rho\left(\overrightarrow{r}×(\overrightarrow{\omega}×\overrightarrow{r})\right) dv=\rho\left(|\overrightarrow{r}|^2\overrightarrow{\omega}-(\overrightarrow{\omega}\cdot\overrightarrow{r})\overrightarrow{r}\right) dv$$

これを領域内で積分（体積分）したものが、剛体全体での角運動量の合計（全角運動量）になります。
積分する領域はＶと置いておきます。
◆参考：ガウスの発散定理（体積分の考え方と公式）

$$全角運動量：\overrightarrow{L}=\int_V\rho(\overrightarrow{r}×\overrightarrow{v}) dv=\int_V\rho\left(|\overrightarrow{r}|^2\overrightarrow{\omega}-(\overrightarrow{\omega}\cdot\overrightarrow{r})\overrightarrow{r}\right) dv$$

内積はスカラーである事に注意して、位置ベクトルの成分表示を（ｘ，ｙ，ｚ）とし、角速度ベクトルの成分表示を（ω_ｘ，ω_ｙ，ω_ｚ）とするとさらに次のように書けます。

$$\overrightarrow{L}=\int_V\rho(x^2+y^2+z^2)\overrightarrow{\omega}dv+\int_V\rho(x\omega_x+y\omega_y+z\omega_z)\overrightarrow{r}dv$$

ここで全角運動量のベクトルも成分ごとに分けると、それら各成分は角速度ベクトルの成分の線型結合で表せるという、ちょっとした規則性を見出せます。全角運動量ベクトルのｘ成分を例として書いてみると、次のようになります。

$$\overrightarrow{L}のx成分：L_x=\int_V\rho\omega_x(x^2+y^2+z^2)dv-x\int_V\rho(x\omega_x+y\omega_y+z\omega_z)dv$$

$$=\omega_x\int_V\rho(x^2+y^2+z^2)dv-\int_V\rho(x^2\omega_x+xy\omega_y+xz\omega_z)dv$$

$$=\omega_x\int_V(y^2+z^2)\rho dv-\omega_y\int_Vxy\rho dv-\omega_z\int_Vxz\rho dv$$

【ｘ^２の項が引き算で消える形になっています。】

全角運動量ベクトルのｙ成分とｚ成分についても同様の形の式になり、全角運動量はある正方行列Ｉと角速度ベクトルの積で表現できる事が言えます。その行列の成分Ｉ_ｉｊの事を「慣性テンソル」と呼び、その対角成分【Ｉ_11, Ｉ₂₂，Ｉ₃₃】は特に「慣性能率」とも呼ばれます。

$$ある3×3行列Iを使って、\overrightarrow{L}=I\overrightarrow{\omega}とも書ける。$$

一様な材質でできた対称性のある剛体の場合（球、円柱、円盤等）、具体的な積分の計算を手計算でも実行する事ができて、慣性能率は比較的簡単な形で表す事ができます。

これらの事は、物理学を専攻する学生さん以外にも、ベクトルやベクトルの外積の応用例を見るのに非常に良い題材の１つになっていると思います。