方向余弦(direction cosine)とはベクトルに対して考えられる補助的な量で、ベクトルの大きさに乗じる事で各成分の値になるような余弦(コーサイン、cos)を指します。(空間ベクトルの平面への射影を考える時の余弦とは一般的に異なるものです。)
この方向余弦の応用として特に重要であるの直交座標同士の座標変換です。
(局所的には直交座標から直交曲線座標への変換もできます。)
■関連記事:ベクトルの内積
「方向余弦」の定義
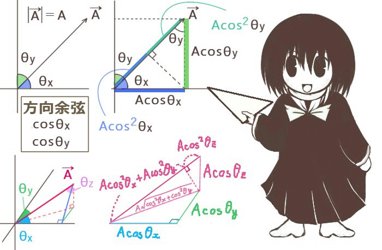
方向余弦とは、ベクトルと座標軸とのなす角に対して考える余弦であり、xyzの空間での直交座標なら1つのベクトルに対して3つ定義されます。平面であれば2つです。
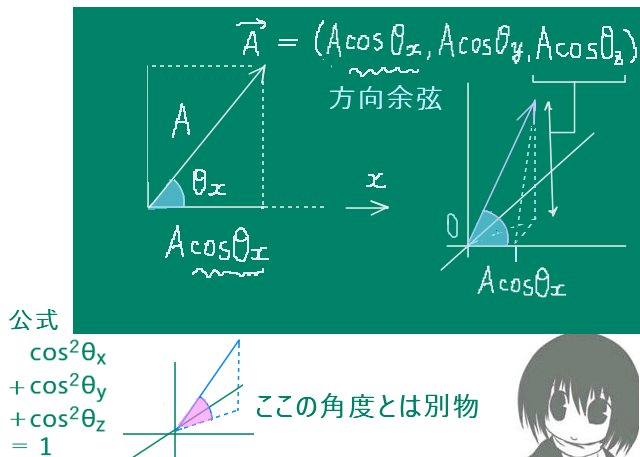
大きさが0でないベクトル\(\overrightarrow{A}\) =(A1,A2,A3)に対して
\(\left|\overrightarrow{A}\right|=A\) ( >0)とおくとして、
\(A\cos\theta_x=A_1\),
\(A\cos\theta_y=A_2\),
\(A\cos\theta_z=A_3\) である時、
余弦 cosθx,cosθy,cosθz を特に「方向余弦」と呼ぶことがあります。
本質的に関数としては普通の余弦 cosθと同じものではありますが、
ベクトルに関する性質と組み合わせる事で特有の関係式がいくつか成立するものになります。
「おおきさが0でないベクトル」という条件を付しているのは、ゼロベクトルに対して方向余弦の定義を適用するとベクトルの大きさも0ですが、成分も全て0なので方向余弦は「任意の角度の余弦」であってもよい事になってしまうからです。
そのため、定義自体をできないわけではありませんがゼロベクトルに対する方向余弦は
「あまり意味のないもの」になってしまうので、ここでは除外して考えるという事です。
方向余弦をベクトルの大きさに乗じる事で、ベクトルの成分が計算されます。
具体的で簡単な数値で考えてみると、例えば(1,1,1)のようなベクトルなら
ベクトルの大きさは\(\sqrt{3}\)なので、各軸に対する方向余弦は3つとも等しく1/\(\sqrt{3}\)になります。
\(\sqrt{3}\cdot\frac{1}{\large{\sqrt{3}}}=1\)であり、大きさ×方向余弦=成分となっています。
この時に、具体的な角度の値は必ずしも分かっていなくてもよい事も多くあります。
cosθ=1/\(\sqrt{3}\)に対しては角度は約54.7°、弧度法で0.955≒0.3πとも書けますが、
角度の値よりも「余弦の値」のほうが重要である場合も少なからずあります。
(特にこの記事で見て行く方向余弦の公式や諸性質・応用ではその傾向があります。)
このように方向余弦の定義自体は比較的簡単なものですが、
注意すべき点があるとすれば方向余弦は3次元の空間の場合には一般的に
「ベクトルをxy平面やxz平面に射影する余弦とは異なる」という事です。
平面であれば、方向余弦はx軸あるいはy軸に対してベクトルを射影する余弦でもあります。
空間の場合でも確かに「軸に対する射影」を行うベクトルであるとは言えますが、それはxy平面等の「平面に対する射影」とは異なるのです。
図で見ると、一般的に3次元空間でのベクトルの方向余弦はxy平面等に対して「斜めになった平面」における直角三角形の1つの角に対する余弦となります。
公式1:方向余弦の2乗和に対する公式
方向余弦は普通の余弦と同じく三角比や三角関数の公式が使えますが、特に方向余弦に対して成立する公式として「3つの方向余弦(平面であれば2つ)の2乗の和は1になる」というものがあります。
3次元空間における3つの方向余弦に対しては次式が成立します。
$$\large{\cos^2\theta_x+\cos^2\theta_y+\cos^2\theta_z=1}$$
平面では次式です。
(空間で1つの方向余弦だけが0と考えても同じ。)
$$\large{\cos^2\theta_x+\cos^2\theta_y=1}$$
この公式は「方向余弦」について成立するものであり、
一般の余弦 cosθで成り立つものではありません。
平面の場合では図を見ると実質的には sin2θ+cos2θ=1 と同じである事も分かるでしょう。
この公式は式で考えても導出できますし、図による平面幾何的な導出も可能です。
(式で考えたほうが、実はやや簡単かもしれません。)
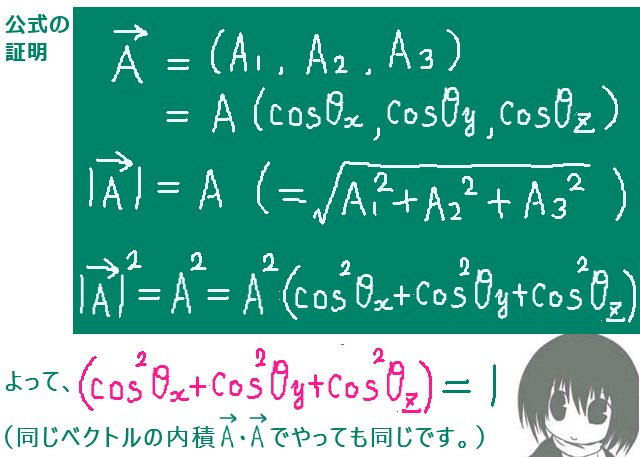
証明
式で見る場合には、ベクトルの大きさ(の2乗)を成分で敢えて表してみると公式がすぐに出ます。(同じベクトルでの内積で考えても同じです。)
ベクトルの大きさをAとすると方向余弦を使った成分は
(A cosθx,A cosθy,A cosθz)です。ここでA>0であるとします。
成分を使って敢えて大きさの2乗を計算すると
A2 cos2θx+A2 cos2θy+A2 cos2θzです。
しかし考えているベクトルの大きさは A なのですから、その式の値はA2です。
A2 cos2θx+A2 cos2θy+A2 cos2θz=A2
A>0なので
cos2θx+cos2θy+ cos2θz=1となり、公式が導出されます。
図で見る場合は、平面だと分かりやすくて式で見る場合と同じように三平方の定理で斜辺の長さを見れば数式だけで考えた時と同じ式を得ます。
また、同じ角度で三角比の意味での余弦を2回考えるという方法も可能です。
すなわち長さ A の斜辺に対して A cosθ を考えて、さらにそこを斜辺とする線分を探します。
するとベクトルが作る直角三角形において直角の頂点から斜辺に垂線を下ろした時に、
そこを境にA cos2θxの長さの部分とA cos2θyの長さに分かれる部分となる事が分かります。
空間の場合も似た考察ができますが、平面と比べるとどうしても単純さが失われる傾向があります。
三平方の定理を使うのが一番早く、式で考える場合と結局同じになります。
それ以外の方法だと、かえって複雑です。
図形的にはベクトルの辺はA cos2θx+A cos2θyの部分とA cos2θzの部分に分かれます。
いずれにしても、方向余弦に関しての性質を調べる時には平面の場合は図形的な考察は比較的容易でも、空間の場合では式で取り扱ったほうが見やすい事を示唆しています。
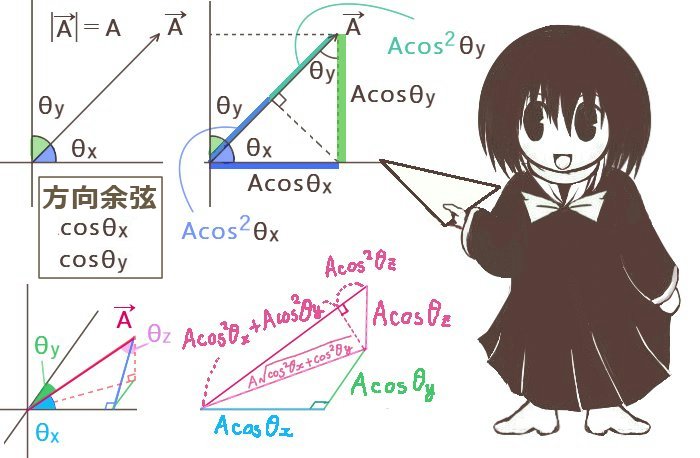
平面の場合は図で見ても比較的分かりやすいですが、空間の場合だとやや複雑になる傾向があります。後述していく方向余弦の関係式や公式の証明では基本的に内積などの式による計算を使っています。
公式2:ベクトルの直線に対する射影についての関係式
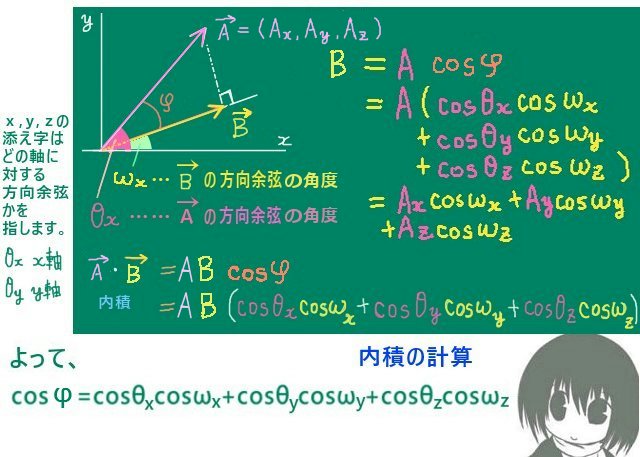
ベクトル\(\overrightarrow{A}\) =(A1,A2,A3)と始点のみを共有する直線があるとして、
始点からの長さが「その直線への\(\overrightarrow{A}\)の射影に等しい」ベクトルを\(\overrightarrow{B}\) とします。
どちらのベクトルもゼロベクトルではないとします。
その他、次のように設定を考えます。
- \(\overrightarrow{B}\) =(B1,B2,B3)とします。
- \(\overrightarrow{A}\)と\(\overrightarrow{B}\) とのなす角をφとします。
- \(\overrightarrow{A}\)の方向余弦の角度をθx,θy,θzとします。
- \(\overrightarrow{B}\)の方向余弦の角度をωx,ωy,ωzとします。
- ベクトルの大きさについては\(\left|\overrightarrow{A}\right|=A\)( >0)および \(\left|\overrightarrow{B}\right|=B\)( >0) とおきます。
この時、B=A cosφ ですが、他にも次の公式が成立します。
上記の設定のもとで、次式が成立します。
$$\large{\cosφ=\cos\theta_x\cos\omega_x+\cos\theta_y\cos\omega_y+\cos\theta_z\cos\omega_z}$$
$$\large{B=A_x\cos\omega_x+A_y\cos\omega_y+A_z\cos\omega_z}$$
これらの式が一体何を言っているのかというと、
最初の式は2つのベクトルのなす角の余弦を互いの方向余弦の積の和で表せる事、
2式目は1つのベクトルの大きさを3つの方向余弦と
「射影のもとになっている別のベクトルの成分」で表せるという事です。
また、1式目は2式目を導出するのに使う式でもあります。
証明
第1式の証明は内積を使います。また、第1式から第2式を証明できます。
ベクトルの成分表示を方向余弦を使って書き、内積をとります。
\(\overrightarrow{A}\) =(A1,A2,A3)=A (cosθx,cosθy,cosθz)
\(\overrightarrow{B}\) =(B1,B2,B3)=B (cosωx,cosωy,cosωz)
\(\overrightarrow{A}\cdot\overrightarrow{B}\)=AB (cosθxcosωx+cosθycosωy+cosθzcosωz)
他方で\(\overrightarrow{A}\cdot\overrightarrow{B}\)=AB cosφ なので、
AB cosφ=AB (cosθxcosωx+cosθycosωy+cosθzcosωz)
A>0かつB>0よりAB>0なので
cosφ=cosθxcosωx+cosθycosωy+cosθzcosωz
次に2式目については、Acosφ=B の関係式に1式目の結果を代入します。
A cosθx=Ax等の関係を使って途中の変形を行います。
B=Acosφ
=A (cosθxcosωx+cosθycosωy+cosθzcosωz)
=(A cosθx) cosωx+(A cosθy) cosωy+(A cosθz) cosωz
=Axcosωx+ A ycosωy+Azcosωz
この2式目のほうの式は、次に見て行くように2つの直交座標においてベクトルの成分の変換公式を導出するのに必要です。(直交座標から直交曲線座標への変換も局所的には可です。)
公式3:2つの直交座標系でのベクトル成分の変換公式
原点を共有する2つの異なる直交座標を考えます。1つの直交座標に対して、もう片方の直交座標が原点を共有した状態で回転したような位置関係です。
この時のベクトルの成分に対する座標変換に対して、方向余弦を使う事ができます。
ここで言う「ベクトルの成分に対する座標変換」とは、
1つの直交座標における成分で表されたベクトルが、空間での大きさと向きは同じにしたままで
「別の直交座標から見た時」にはどのような成分で書けるだろうか?という問題です。
得られる公式は形が規則的ではあるのですが、3軸の3軸に対する方向余弦を考える必要があるので合計9個の方向余弦を必要とします。
それらは1~3の番号の組み合わせを使うと処理をしやすい場合もありますが
(線形変換的な式なので、特に行列などを使う場合など)、
ここではx,y,zとX,Y,Zの文字で区別を行う事にします。
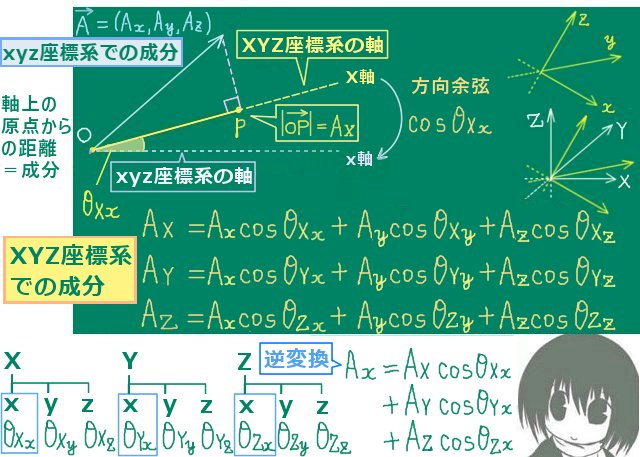
原点を共有するxyz系とXYZ系の2つの直交座標軸があり、
片方はもう片方に対して原点回りに回転したような位置配置となっているとします。
この時にx,y,zの軸上のベクトルからX,Y,Zの軸への方向余弦を考えます。
x軸上のベクトルに対するY軸への方向余弦を cosθxYのように書く事にすると、
xyz座標系で成分を考えたベクトル\(\overrightarrow{A}\) =(Ax,Ay,Az)(\(\neq\overrightarrow{0}\))を
XYZ座標系の成分(AX,AY,AX)で書く時の変換の式は次のようになります。
- AX=AxcosθXx +AycosθXy +AzcosθXz
- AY=AxcosθYx +AycosθYy +AzcosθYz
- AZ=AxcosθZx +AycosθZy +AzcosθZz
また、逆にXYZ座標系の成分で書かれた(AX,AY,AX)を
xyz座標系の成分(Ax,Ay,Az)で書くには次のような変換をします。
- Ax=AXcosθXx +AYcosθYx +AZcosθZx
- Ay=AXcosθXy +AYcosθYy +AZcosθZy
- Az=AXcosθXz +AYcosθYz +AZcosθZz
後述しますが、2つの異なるベクトルに対してこの変換を適用した時に
2つのベクトルの内積は変換前と変換後で値は同じ(=不変)になります。
(そこから前提である2つのベクトルの大きさも変換の前後で値は同じという事も見れます。)
ここでも考えているベクトルはゼロベクトルを除いていますが、考えている2つの直交座標系は原点を共有しているという設定なので、原点におけるゼロベクトルはそもそも変換の必要はなくどちらの座標系でも同じ成分(0,0,0)として共有されている事になります。
上記の変換の3式は線形結合の形なので、次のように行列の積で表現する事もできます。
また、方向余弦の添え字が一定の規則性を持つので行と列に上手く対応させる事ができます。
$$
\left(\begin{array}{c}
A_X\\
A_Y\\
A_Z\end{array}\right)
=
\left(\begin{array}{lcr}
\cos\theta_{Xx} &\cos\theta_{Xy}&\cos\theta_{Xz}\\
\cos\theta_{Yx} &\cos\theta_{Yy}&\cos\theta_{Zy}\\
\cos\theta_{Zx} &\cos\theta_{Yz}&\cos\theta_{Zz}\end{array}\right)
\left(\begin{array}{c}
A_x\\
A_y\\
A_z\end{array}\right)
$$
3行3列程度ならわざわざ行列にするよりも普通に式で書く方が早いし分かりやすいと見るか、
行列で見たほうが規則性が明らかで書く手間も少し減ると見るかは人それぞれと思われます。
9つの方向余弦の位置関係を表にして整理すると次のようになります。
| 方向余弦 | X軸から | Y軸から | Z軸から |
| x軸へ | cosθXx | cosθYx | cosθZx |
| y軸へ | cosθXy | cosθYy | cosθZy |
| z軸へ | cosθXz | cosθYz | cosθZz |
余弦が角度のプラスマイナスで同じ値になる事を考えると、これらの方向余弦は「xyz系の軸からXYZ系の軸への方向余弦」を考えた時と同じ値になります。つまり例えば「z軸からY軸への方向余弦」は「Z軸からy軸への方向余弦cosθZy」と同じものを使ってよいという事です。
ただしxyz系の軸からXYZ系変換への公式は導出過程に由来して、
単純にx,y,zとX,Y,Zの置き換えをすればよいわけではなく
「x軸から考えた場合の3つの方向余弦」を使う必要があります。
表で言うと、
XYZ系への変換では1つの変換につき「縦」の3つを使うのに対して、
xyz系への変換では1つの変換につき「横」の3つを使う事になります。
ここで具体的な角度よりも「余弦の値」自体のほうが基本的に重要となる事を考えて、
方向余弦を cosθXy=CXyのように略記すると次のように書けます。
| 方向余弦 | X軸から | Y軸から | Z軸から |
| x軸へ | CXx | CYx | CZx |
| y軸へ | CXy | CYy | CZy |
| z軸へ | CXz | CYz | CZz |
さらに、添え字をアルファベットではなく1~3の番号だけで書くと次のようになります。
| 方向余弦 | X軸から | Y軸から | Z軸から |
| x軸へ | C11 | C12 | C13 |
| y軸へ | C21 | C22 | C23 |
| z軸へ | C31 | C32 | C33 |
変換後の式が線形変換の形になっている事に由来して方向余弦の配列を行列として扱う時には、添え字の組み合わせと行・列の番号が一致するので便利な事もあります。また、和をシグマ記号で表したい時も添え字がアルファベットではなく番号になっているほうが便利です。
ただし2種類の添え字を同じ1~3の番号で表すと、どの軸からどの軸への方向余弦を考えているかといった図的な位置関係は少し見えにくくなります。そのため、この記事では番号ではなくアルファベットによる添え字を使用しています。いずれの表示方法でも表現する事自体は同じです。
この公式の変換は原点を始点として考えていますが、任意の点を始点とする場合でもそこを基準に考えるかベクトルを原点に平行移動して考える事によって変換公式を適用する事ができます。直交座標系ではベクトルの向き(および大きさ)を保ったまま平行移動を行っても軸とのなす角は同じ値に保たれます。つまり方向余弦の値も同じものが使えるので、上記の変換公式を適用できます。
証明
変換公式の証明には前述の「ベクトルの直線への射影と方向余弦の関係式」を使います。本質的には、意味を把握しているならその関係式に当てはめる事で変換の式はそのまま導出できます。
前述の公式を書くと次の通りです。
ここでは射影ベクトルの始点からの距離を表すほうの式だけを使います。
$$\large{B=A_x\cos\omega_x+A_y\cos\omega_y+A_z\cos\omega_z}$$
変換公式の証明用に変数を対応させると次のようになります。
$$\large{A_X=A_x\cos\theta_{Xx}+A_y\cos\theta_{Xy}+A_z\cos\theta_{Xz}}$$
実はこれで変換公式の証明に既になってしまっているのですが、
以下もう少し詳しく説明を加えます。
まず、xyz系からXYZ系への変換を考えたいので
「AXをAx,Ay,Azと方向余弦で表す」事を考えます。
そこで、ベクトル\(\overrightarrow{A}\)のXYZ系の各軸への射影を1つずつ考えます。
すると、ベクトルの終点から軸に下ろした垂線の足と始点までの距離は、
実はそれがそのまま「XYZ系における座標成分」になっています。
すると「X軸からのx軸」「X軸からのy軸」「X軸からのz軸」への方向余弦を考えて、公式に当てはめればXYZ系でのベクトル\(\overrightarrow{A}\)の「X成分」が得られるという流れです。
それが AX=AxcosθXx +AycosθXy +AzcosθXzの式になります。
Y軸についても同様に「Y軸からのx軸」「Y軸からのy軸」「Y軸からのz軸」への方向余弦を考え、
Z軸についても同様に「Z軸からのx軸」「Z軸からのy軸」「Z軸からのz軸」への方向余弦を考えて
AY=AxcosθYx +AycosθYy +AzcosθYz および
AZ=AxcosθZx +AycosθZy +AzcosθZz の式を得ます。
逆変換の式の場合
同じ考え方で、XYZ系の成分で表されたベクトルをxyz系の成分で表す逆変換の式も作れます。
ただし「考え方」が同じでも使う方向余弦が違ってくるので注意も必要です。【余弦の値自体はx軸からY軸の方向余弦はY軸からx軸への方向余弦と同じものを使えます。cosθ=cos(-θ)であるため。】
xyz系からの変換を考える時には、使う方向余弦は次のようになります。
| Axを表すために使う方向余弦 | Ayを表すために使う方向余弦 | Azを表すために使う方向余弦 |
| 「x軸からX軸」cosθXx 「x軸からY軸」cosθYx 「x軸からZ軸」cosθZx | 「y軸からX軸」cosθXy 「y軸からY軸」cosθYy 「y軸からZ軸」cosθZy | 「z軸からX軸」cosθXz 「z軸からY軸」cosθYz 「z軸からZ軸」cosθZz |
XYZ系からの変換の時とは微妙に違っていて、各変換の式で使用する方向余弦のうち1つは共通していて残り2つは異なっています。(行列表示で言えばcosθXxなどの対角成分は共通していて、残り2つが違うものになっています。)
式で使うベクトル\(\overrightarrow{A}\)の成分についてはXYZ系での成分であるAx,Ay,Azを使用します。
これらによって、xyz系での成分であるAx,Ay,Azを表す式を得るわけです。
すなわち
Ax=AXcosθXx
+AYcosθYx
+AZcosθZx
Ay=AXcosθXy
+AYcosθYy
+AZcosθZy
Az=AXcosθXz
+AYcosθYz
+AZcosθZz の3式が導出されます。
局所的には直交曲線座標への変換にも適用可能である件
上記の方向余弦による直交座標間のベクトルの変換公式は、
局所的には極座標や球面座標などの「直交曲線座標」にも適用可能です。
その事についてもここで簡単に触れておきます。
ここで「局所的に」というのは、直交曲線座標においては1つ1つの点において2つまたは3つの座標曲線(極座標だと同心円と放射状に伸びる直線)の接線ベクトルが互いに直交するので、そこに限定して見れば「直交座標とみなせる」という事を指します。
ただし直交曲線座標では一般的に、そのような局所的には直交座標の軸とみなせる接線ベクトルも位置を変えれば向きが変わってしまいます。ですので直交曲線座標においては「向きが異なる局所的な直交座標」が至るところに存在するという感じです。
そのため、直交曲線座標に対して上記の変換公式を使う時には方向余弦を微分や偏微分を使って表します。そのようにする事で、変換の式が座標変数による関数として表せるので、結果的に領域全体での変換を表す事が可能になります。これは微分方程式に対して基本ベクトルを変更する形での極座標変換を行う時などに重要になります。
基本ベクトルを変更しない形での微分方程式の極座法変換もあり、その場合には方向余弦を使った公式は不要になります。
方向余弦を使った変換公式を適用する必要があるのは力ベクトルなども含めたベクトル場の成分をx,y,zではなくr,θ,φで表し、rやθによる変化を考えたい場合です。
公式4:直交座標変換における方向余弦の関係式
上記は9つの方向余弦を使った「成分についての座標変換の公式」でしたが、
9つの方向余弦自体に対して成立する関係式も公式として存在します。
■ J,K =X,Y,Z のそれぞれ(J≠K)に対して次式が成立します。
$$\large{
\cos\theta_{Jx}\cos\theta_{Kx}+\cos\theta_{Jy}\cos\theta_{Ky}+\cos\theta_{Jz}\cos\theta_{Kz}=0
}$$
■ j=x,y,z のそれぞれに対して次式が成立します。
$$\large{
\cos^2\theta_{Xj}+\cos^2\theta_{Yj}+\cos^2\theta_{Zj}=1
}$$
■ j, k = x,y,z のそれぞれ(j≠k)に対して次式が成立します。
【j=kの時は第2式になります。】
$$\large{
\cos\theta_{Xj}\cos\theta_{Xk}+\cos\theta_{Yj}\cos\theta_{Yk}+\cos\theta_{Zj}\cos\theta_{Zk}=0
}$$
■J=X,Y,Z のそれぞれに対して次式が成立します。
(第1式の左辺でJ=Kとした時に相当。)
$$\large{
\cos^2\theta_{Jx}+\cos^2\theta_{Jy}+\cos^2\theta_{Jz}=1
}$$
J≠Kおよびj≠kのもとで
第1式の意味は「XYZ系の2つの軸からのxyz系の1つの軸への方向余弦の積の和は0になる」
第2式の意味は「xyz系の1つの軸からのXYZ系の各軸への方向余弦の2乗和は1になる」
第3式の意味は「xyz系の2つの軸からのXYZ系の1つの軸への方向余弦の積の和は0になる」
という事になります。
第3式でj=kとした場合が第2式、
第1式でJ=Kとした場合が第4式であり、値が変わる事になります。
(j=kとj≠kおよびJ=KとJ≠Kの場合分けで全体を2式にまとめる事もできます。)
第2式と第4式は、空間内の直交座標系の任意のベクトルに対して「各軸への方向余弦の2乗和は1になる」という公式と実は同じものであるという見方もできます。
これらの公式は「暗記」するようなものではなく、このような規則的な関係が成立するという認識のもと、もし必要であれば適宜参照すればよいと考えるべきでしょう。後述する「原点を共有する直交座標間の変換の前後でベクトルの内積は不変である」事の証明ではこれらの関係式の一部を使います。

$$
\left(\begin{array}{c}
A_X\\
A_Y\\
A_Z\end{array}\right)
=
\left(\begin{array}{lcr}
\cos\theta_{Xx} &\cos\theta_{Xy}&\cos\theta_{Xz}\\
\cos\theta_{Yx} &\cos\theta_{Yy}&\cos\theta_{Zy}\\
\cos\theta_{Zx} &\cos\theta_{Yz}&\cos\theta_{Zz}\end{array}\right)
\left(\begin{array}{c}
A_x\\
A_y\\
A_z\end{array}\right)
=\left(\begin{array}{lcr}
C_{11} &C_{12}&C_{13}\\
C_{21} &C_{22}&C_{23}\\
C_{31} &C_{32}&C_{33}\end{array}\right)
\left(\begin{array}{c}
A_x\\
A_y\\
A_z\end{array}\right)$$
のように方向余弦を略記して、さらに行列の要素に対応する番号で表す時には
上記の公式は次のようにも書けます。
$$\sum_{n=1}^3C_{Jn}C_{Kn}=0\hspace{5pt}(J\neq K)$$
$$\sum_{n=1}^3(C_{nj})^2=1$$
$$\sum_{N=1}^3C_{Nj}C_{Nk}=0\hspace{5pt}(j\neq k)$$
$$\sum_{n=1}^3(C_{Jn})^2=1$$
(J,K=1,2,3は、ここでは行の番号です。j,k=1,2,3はここでは列の番号。)
| 公式 | 例 | 行列要素での表記 |
| cosθJxcosθKx +cosθJycosθKy +cosθJzcosθKz=0 (J≠Kの時) | cosθXxcosθZx +cosθXycosθZy +cosθXzcosθZz=0 【X,Z軸からの方向余弦の積の和】 | $$\sum_{n=1}^3C_{Jn}C_{Kn}=0\hspace{5pt}(J\neq K)$$ |
| cos2θXj +cos2θYj +cos2θZj=1 (第3式でj=kの時) | cos2θXy +cos2θYy +cos2θZy=1 【y軸への方向余弦の2乗和】 | $$\sum_{n=1}^3(C_{nj})^2=1$$ |
| cosθXjcosθXk +cosθYjcosθYk +cosθZjcosθZk=0 (j≠kの時) | cosθXxcosθXz +cosθYxcosθYz +cosθZxcosθZz=0 【x,z軸への方向余弦の積の和】 | $$\sum_{N=1}^3C_{Nj}C_{Nk}=0\hspace{5pt}(j\neq k)$$ |
| cos2θJx +cos2θJy +cos2θJz=0 (第1式でJ=Kの時) | cos2θZx +cos2θZy +cos2θZz=0 【Z軸からの方向余弦の2乗和】 | $$\sum_{n=1}^3(C_{Jn})^2=1$$ |
証明
証明はいずれも内積計算を使いますが、2乗和の形の式はそれ以外の方法でもできます。
ここで考えるベクトルは任意のベクトルではなく「始点と終点が軸上にあるベクトル」です。
以下、そのようなベクトルを「軸に重なるベクトル」と呼ぶ事にします。
1つの座標系における軸に重なるベクトルであっても、別の座標系から見た成分で書くと通常のベクトルとして扱われる事になり、その事をここでの証明でも使います。
第1式
第1式については、X,Y,Z軸の異なる2つの軸は直交しますから、それらの軸上のベクトル同士の内積は0です。そこで、ベクトルの成分で内積を計算して0に等しいとする事で証明されます。(同じ1つの軸同士【公式でJ=K】であれば当然直交はせず、内積は大きさの2乗になります。それは第4式の証明です。)
J≠Kの時に J 軸と K 軸(例えばX軸とZ軸)は直交するので、
大きさが P(>0)のJ軸上のベクトル\(\overrightarrow{P}\)について成分はxyz系での座標で書ける事に注意すると
\(\overrightarrow{P}\)= P (cosθJx,cosθJy,cosθJz)
同じように大きさがQ(>0)であるK軸に重なるベクトル\(\overrightarrow{Q}\) は次のように書けます。
\(\overrightarrow{Q}\)= Q (cosθKx,cosθKy,cosθKz)
2つのベクトルは直交するので内積は0であり、
\(\overrightarrow{P}\cdot\overrightarrow{Q}\)=PQ(cosθJxcosθKx+cosθJycosθKy+cosθJzcosθKz)=0
PQ≠0なので J≠K であれば
cosθJxcosθKx+cosθJycosθKy+cosθJzcosθKz=0
第2式
第2式については、xyz系の軸に重なるベクトルから見て考えます。
xyz系のj軸(例えばy軸)に重なる大きさ(p>0)のベクトル\(\overrightarrow{p}\)を考えて、
成分をXYZ系の座標として書きます。
方向余弦はXYZ系からxyz系へのものを選んで使う事ができ、
k軸からX,Y,Zに向かうものを選ぶ事に注意すると次のように書けます。
\(\overrightarrow{p}\)= p (cosθXj,cosθYj,cosθZj)
同じベクトル同士の内積\(\overrightarrow{p}\cdot\overrightarrow{p}\)を考えるか、
成分で計算したベクトルの大きさ=p2と考える事で結果の式を得ます。
\(\overrightarrow{P}\cdot\overrightarrow{P}\)=p2(cos2θXj+cos2θYj+cos2θZj)=p2
p>0なので
cos2θXk+cos2θYk+cos2θZk=1
この式は第3式でj=kとして考えた場合でもあります。
第3式
第3式はxyz系から見て、第1式の時と同じように考えます。
j,k=x,y,zでj≠kのもとで、p>0およびq>0が大きさである
j軸とk軸に重なる2つのベクトルを考えると、2つのベクトルは直交します。
両者をXYZ系の座標で書き、内積を成分で計算して0になるとおくと結果の式を得ます。
\(\overrightarrow{p}\)= p(cosθXj,cosθYj,cosθZj)
\(\overrightarrow{q}\)= q (cosθXk,cosθYk,cosθZk)
\(\overrightarrow{p}\cdot\overrightarrow{q}\)=pq(cosθXjcosθXk+cosθYjcosθYk+cosθZjcosθZk)=0
p>0かつq>0なのでj≠kであれば
cosθXjcosθXk+cosθYjcosθYk+cosθZjcosθZk=0
第4式
第4式は、第1式において大きさがP (>0)の1つのベクトル同士の内積か大きさを成分で計算する事で結果の式を得ます。
\(\overrightarrow{P}\cdot\overrightarrow{P}\)=P2(cos2θJx+cos2θJy+cos2θJz)=P2
P>0なので
cos2θJx+cos2θJy+cos2θJz=1
第2式と第3式はxyz系から見て計算を考えましたが、得られた方向余弦の関係式はXYZ系をxyz系に変換する場合でも成立しているので必要があれば使ってもよい事になります。
また、第2式と第4式に関しては成分を考えている座標系だけから見れば「ある1つのベクトル」を考えている事になります。そのため、前述の「方向余弦の2乗和は1になる」という公式と実は同じものであるという見方もできます。
方向余弦を使った直交座標の変換の前後において内積は不変である事の証明
座標変換をした時に値が変わらない量(「不変量」)についての考察は数学的に重要で、扱う対象によっては物理学でも重要となる場合もあります。
ところで前述の原点を「共有する直交座標同士のベクトルの成分の変換」は、ベクトル自体はいじっていないはずなので変換前と変換後で大きさは「同じはず」です。もしも、現に計算したらベクトルの大きさの値が変わってしまうなどという結果が出たら整合性がとれず困った事になります。
しかし実際は計算をしてもベクトルの大きさは同じ値に保たれる事が数式でも分かります。
そして実は、変換前と変換後ではベクトルの大きさだけでなく内積が同じ値に保たれているのです。
2つのベクトルの成分を、原点を共有する2つの直交座標間で変換するとします。
\(\overrightarrow{A}\) =(Ax,Ay,Az)および\(\overrightarrow{B}\) =(Bx,By,Bz)を考えて、
変換後の座標はそれぞれ
(AX,AY,AZ)および(BX,BY,BZ)であるとします。
この時に2つのベクトルの内積\(\overrightarrow{A}\cdot\overrightarrow{B}\) の値は、変換前のxyz系の座標成分で計算しても、
変換後の座標成分で計算しても同じ値になります。
$$\overrightarrow{A}\cdot\overrightarrow{B}=A_xB_x+A_yB_y+A_zB_z=A_XB_X+A_YB_Y+A_ZB_Z$$
同じベクトル同士の内積を考える事により、
変換の前後でベクトルの大きさも同じ値に保たれる事も確認される事になりす。
(外積ベクトルについては変換によって異なるベクトルに変化してしまいます。)
証明
変換後の成分で内積を計算し、変換前の内積の値に等しくなる事を示します。
2つのベクトルの変換について、使用する方向余弦は「座標軸から座標軸へのもの」なので共通して使う事ができます。
- AX=AxcosθXx +AycosθXy +AzcosθXz
- AY=AxcosθYx +AycosθYy +AzcosθYz
- AZ=AxcosθZx +AycosθZy +AzcosθZz
- BX=BxcosθXx +BycosθXy +BzcosθXz
- BY=BxcosθYx +BycosθYy +BzcosθYz
- BZ=BxcosθZx +BycosθZy +BzcosθZz
さて、これの内積を計算するとなるとX成分だけで見ても9つの項ができる事になりますが
規則性があるので全体としても3項の和の塊が9つという形です。
さらに前述の座標変換時の方向余弦に関する関係式を使うと、実は多くの部分が0になるのです。
- AxBxcos2θXx+AxBxcos2θYx+AxBxcos2θZx=AxBx
【∵cos2θXx+cos2θYx+cos2θZx=1】 - AxBycosθXxcosθXy+AxBycosθYxcosθYy+AxBycosθZxcosθZy=0
【∵cosθXxcosθXy+cosθYxcosθYy+cosθZxcosθZy=0】 - AxBzcosθXxcosθXz+AxBzcosθYxcosθYz+AxBzcosθZxcosθZz=0
【∵cosθXxcosθXz+cosθYxcosθYz+cosθZxcosθZz=0】 - AyBycos2θXy+AyBycos2θYy+AyBycos2θZy=AyBy
【∵cos2θXy+cos2θYy+cos2θZy=1】 - AyBxcosθXycosθXx+AyBxcosθYycosθYx+AyBxcosθZycosθZx=0
【∵cosθXxcosθXy+cosθYxcosθYy+cosθZxcosθZy=0(2番目の計算と同じ)】 - AyBzcosθXycosθXz+AyBzcosθYycosθYz+AyBzcosθZycosθZz=0
【∵cosθXycosθXz+cosθYycosθYz+cosθZycosθZz=0】 - AzBxcosθXzcosθXx+AzBxcosθYzcosθYx+AzBxcosθZzcosθZx=0
【∵cosθXxcosθXz+cosθYxcosθYz+cosθZxcosθZz=0(3番目の計算と同じ)】 - AzBycosθXzcosθXy+AzBycosθYzcosθYy+AzBycosθZzcosθZy=0
【∵cosθXycosθXz+cosθYycosθYz+cosθZycosθZz=0(6番目の計算と同じ)】 - AzBzcos2θXz+AzBzcos2θYz+AzBzcos2θZz=AzBz
【∵cos2θXz+cos2θYz+cos2θZz=1】
ここでは一応全部記してみましたが、
「2番目と5番目」「3番目と7番目」「6番目と8番目」は
掛け合わせる方向余弦の順番が違うだけで実質的に同じ計算であり、しかも値が0になります。
つまり6式については実は3組のほぼ同じ計算の式で、しかも0になって消えるわけです。
残るのは他の3つだけで、それらは方向余弦の部分が上手い具合に1になります。
よって、XYZ系に成分を変換後の内積の値は
AxBx+AyBy+AzBzとなり、
これは変換前の内積の値に一致するわけです。

XYZ系からxyz系への逆変換の式でも、内積の不変性は同様に証明も同様に可能です。
乗じる項の順番が異なるだけで実質的に同じ計算になる2組の箇所が3つあったのはあながち偶然ではなくて、実は行列の非対角部分でC12とC21のような転置の配置にある要素の組がそれらに該当します。
また、計算結果が0にならなかった部分は対角部分の3つです。
ここでの変換の場合に方向余弦が行列の要素に対応するような結果の式であったので、そのような規則性が見れるわけです。
上記の証明について、シグマ記号を使った証明も記します。
番号を使ってやる事も可能ですが、ここではアルファベットのままやる方法を書きます。
方向余弦はcosθXz=CXzのような略記号を使います。$$\large{\overrightarrow{A}\cdot\overrightarrow{B}=\sum_{J=X,Y,Z}A_JB_J}$$
$$\large{=\sum_{J=X,Y,Z}\left\{\left(\sum_{j=x,y,z}C_{Jj}A_j\right)\left(\sum_{k=x,y,z}C_{Jk}B_k\right)\right\}}$$
$$\large{=\sum_{J=X,Y,Z}\left(\sum_{j,k=x,y,z}C_{Jj}C_{Jk}A_jB_k\right)}$$
$$\large{=\sum_{j,k=x,y,z}\left\{A_jB_k\left(\sum_{J=X,Y,Z}C_{Jj}C_{Jk}\right)\right\}}$$
この式をよく見ると、1つのJを決めてj,k=x,y,zについて加え合わせた時に、
前述の公式によりj=kの場合以外は0になる事が分かります。
$$j\neq kの時、\large{
\cos\theta_{Xj}\cos\theta_{Xk}+\cos\theta_{Yj}\cos\theta_{Yk}+\cos\theta_{Zj}\cos\theta_{Zk}=0なので、
}$$
$$j\neq kの時、\large{A_jB_k\left(\sum_{J=X,Y,Z}C_{Jj}C_{Jk}\right)=0}$$
よって内積はk=jの項だけ考えればよい事になりますが、
k=jの時は同じ形の式が1になるので結局、方向余弦は全て式から無くなります。
整理すると、次のようになります。
$$
\large{\overrightarrow{A}\cdot\overrightarrow{B}=\sum_{j=x,y,z}\left\{A_jB_j\left(\sum_{J=X,Y,Z}C_{Jj}C_{Jj}\right)\right\}}
$$
$$\large{=\sum_{j=x,y,z}\left(A_jB_j\right)}$$
これによってXYZ系の成分による内積の結果と、
xyz系の成分による内積の結果が等しい事が示されます。