電磁誘導(「でんじゆうどう」)は「磁場が変化する事で起電力が生じる」事を表す現象で、発電機や変圧器の原理です。電磁誘導の法則はマクスウェル方程式の1つで、数式的には磁場の時間変化と電場の回転を含む式になっています。
電磁誘導の法則は、アンペールの法則と組み合わせて電磁波を表す式を導出するための法則でもあります。また、電磁誘導の法則はマクスウェル方程式の中では電気回路論との直接的な関係が強い法則であるとも言えます。そのため、この記事では電磁誘導に関連した回路論の事項もいくつか含まれます。
電磁誘導を考えるにあたって重要となる「誘導起電力」について、記号はVでもEでもεでも何でもよいのですが、この記事では統一してVeという記号で書いておきます、(それほど深い意味はなく、電場等との記号と混同しないようにという意味合いです。)
この法則はいくつか呼ばれ方があって、
「ファラデーの(電磁誘導)法則」「ノイマンの(電磁誘導)法則」「ファラデー・ノイマンの(電磁誘導)法則」あるいは単に「誘導法則」・・・などとも言います。
このサイトでは「電磁誘導の法則」の名称で統一します。
科学史的には、電磁誘導に関する詳しい実験と基本的なアイデアの提唱を行ったのはファラデーであり、その結果を整理して定式化したのはノイマンだとされています。
電磁誘導という現象
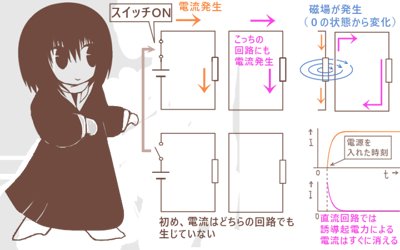
直流電源(起電力の向きが一定)をつないだ回路と電源が無い回路を用意して、電源を入れると電源が無いほうの回路にも一瞬だけ電流が発生します。この現象が電磁誘導です。
この現象は、電源をつないでいない回路に磁石を近づけたり遠ざけたりする時にも起こります。つまり磁場が関係している事が分かります。1つの回路が別の回路に電流を発生させているのは、片方の回路の電流によって発生した磁場であると言えます。
ただし磁場さえあれば同じ現象が起きるかというと実はそうではなく、
「磁場の変化」(つまり増加か減少)があるとそのような事が起きます。また、電源をつないでいない回路に発生する電流の大きさは回路の導線の長さ・断面積・材質で変化します。つまり回路の抵抗に依存します。そのため、磁場の変化によって誘起されるのは電流を生じさせる「起電力」(電源としての電位差)であると考えられるわけです。
- 電磁誘導が起きるのは「磁場の変化」が起きる時
- 磁場の変化によって誘導されるのは回路全体に電位差を作る「起電力」(回路全体の電圧)
電磁誘導は1つの回路の電流による磁場が、電気的には絶縁されている他の回路に対して誘電起電力および結果としての電流を生じさせています。これについては、切り離された2つの電気回路が磁気回路によって接続されているという見方もできます。確かに直流電流が発生させる誘導起電力は「電源を入れた時と切った時だけ」の一瞬ですが、交流電流であれば継続的な交流の誘導起電力を発生し続ける事ができます。
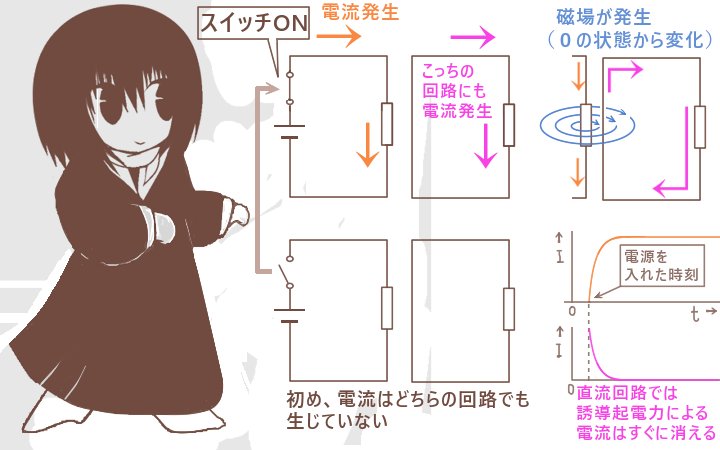
しかも、次に見て行くように発生する誘導起電力は「磁場の変化」の大小で決定し、直接的には電流の大きさには依存しません。すると、何らかの方法で局所的に磁場の変化量を増やせば回路の電圧の調整が可能になります。(具体的には導線をコイル状にして、さらに中に鉄心を入れます。)それを実用化しているのが変電所等に設置されている変圧器です。電磁誘導は発電機の原理でもありますが、変圧器の原理でもあるわけです。
電流が作る磁場を表すアンペールの法則やビオ・サバールの法則は電磁石の原理です。また、磁場中の電荷や電流が生じている導線が受ける電磁力あるいはローレンツの力は電動機(モーター)の原理です。電動機と発電機は実は構造的には基本的にほぼ同じか非常に似た機械であり、電動と発電という用途の違いで区別がされています。

法則の積分形(固定回路で磁場の時間変動がある時)
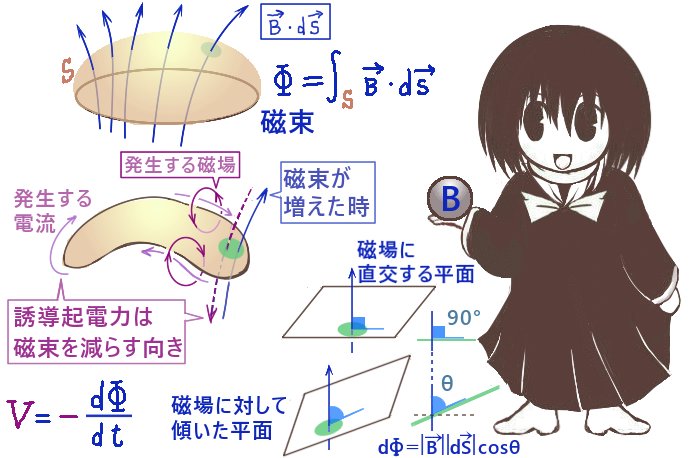
電磁誘導の法則は、磁束と誘導起電力との関係を表した式です。磁束とは磁場の法線面積分で表される量を言います。(\(\overrightarrow{B}\) を「磁束密度」として考える事があるのは磁束の定義に由来します。ただし当サイトではそれを磁場として扱う方式で記述をしています。)
そして誘電起電力を「電気回路一周分で電荷が受ける事になる仕事」として捉えると、電磁誘導の法則は「電場の回転」と「磁場の時間変化」の関係を表す式であるとみなす事ができます。
他の3つのマクスウェル方程式同様に、電磁誘導の法則にも積分形と微分形が存在します。法則の直接的な意味が分かりやすいのは積分形であり、次のようになります。
曲面Sに発生する誘電起電力は、磁束の時間変化で表されます。
誘電起電力や磁束はベクトルではなく、スカラー量です。
$$V_e=-\frac{d\Phi}{dt}=-\frac{d}{dt}\int_S \overrightarrow{B}\cdot d\overrightarrow{s}$$
$$\left(V_e=-\frac{\partial\Phi}{\partial t}=-\frac{d\Phi}{dt}と考えても同じです。\right)$$
特に回路が固定されている時は、
回路が固定されている時には特に磁場の時間変化で表す事ができます。
$$V_e=-\int_S \frac{\partial\overrightarrow{B}}{\partial t}\cdot d\overrightarrow{s}$$
曲面としては基本的には開曲面を考えます。
磁場の関数形は領域で不連続点が無いものとします。
(数学的に\(\large{\frac{d}{dt}\int_S \overrightarrow{B}\cdot d\overrightarrow{s}=\int_S \frac{\partial\overrightarrow{B}}{\partial t}\cdot d\overrightarrow{s}}\) となるための条件。)
また1変数の微分なのか偏微分なのかの問題については、磁束は曲面に対して想定される量なので「時間だけの関数」であり、1変数の微分で扱えます。積分のほうで見ても、積分した結果を考えれば座標成分の変数は残っていない事になるので時間だけの関数です。
面積分は変数としては座標成分だけが関係するので、被積分関数が領域内で連続であれば時間微分(これは偏微分になります)を積分しても同じ結果を得ます。
また、時間微分というのは基本的に偏微分を考えるものであり、
1変数に関しては∂/∂tもd/dtも同じ事なので∂/∂tで統一しても同じ事になります。
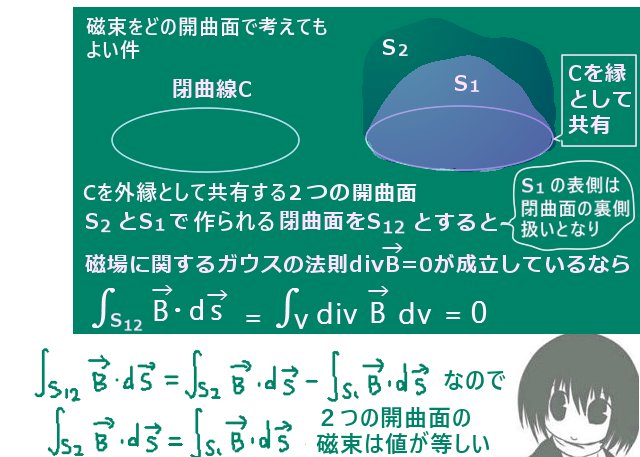
磁束に関しては「閉曲面」に関して任意のものを考えてもよいのですが、それは
「時間変動する磁場の任意の時刻においては静磁場同様に磁場に関するガウスの法則が成立する」のであれば、確かにそう言える事が分かります。
閉曲線Cを外縁として共有する任意の2つの開曲面を考えて、
それらで囲まれる閉曲面内ではどの位置でも磁場の発散が0です。
式で書くと\(\mathrm{div}\overrightarrow{B}=0\) であり、物理的には「湧き出しを持たない」事を意味します。
すると、ガウスの発散定理によって2つの閉曲面上の磁場の法線面積分は等しい値になる事が言えます。すなわち1つの閉曲線Cを外縁として共有している限り、開曲面Sは任意のものを考えても「磁束」\(\large{\int_S\overrightarrow{B}\cdot d\overrightarrow{S}}\) は同じ値になる事が数式的にも保証される事になります。
磁束を考える開曲面の任意性については、てきとうな閉曲面を考える事もできますが磁力線が通過する回路の任意の形状を表すという捉え方もできます。(どちらの捉え方にも意味があります。)
電磁誘導の法則について、発生する誘電起電力の「向き」に着目したものを特にレンツの法則と呼ぶ事もあります。
電磁誘導における誘導起電力は、
「回路を通過する磁束の変化を妨げるような電流を発生させる向き」に生じます。
つまり磁束が増えるなら減らすような磁場を作る電流を発生させる向きに誘電起電力が発生し、磁束が減るなら増やす方向に誘導起電力が発生します。
(ただし、それで実際に電流がどれだけ多く発生するかはまた別問題となります。)
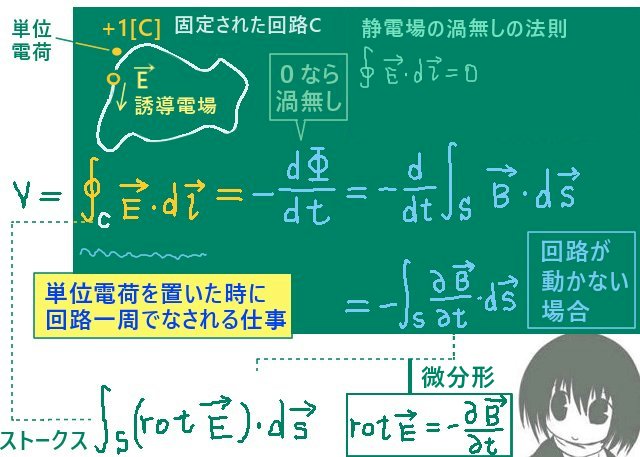
起電力の発生とは回路全体に電位差が生じる事です。その結果として回路には電流が発生します。この時に回路の導線に沿って電場が発生していると考えて、それを特に誘導電場と呼ぶ事があります。
この時に、+1 [C]の電荷を置いてみた時に誘導電場から受ける仕事が「回路全体に生じている電位差」(=起電力)であるので、それは回路1周分の電場(=+1 [C]の電荷が受ける電気力)の接線線積分で表す事ができます。
$$\oint_C\overrightarrow{E}\cdot d\overrightarrow{l}=-\frac{\partial\Phi}{\partial t}\left(=-\frac{d\Phi}{dt}\right)$$
特に回路が固定されている時は次式です。
マクスウェル方程式の1つとして見る場合は基本的にこの形のものを指します。
$$\oint_C\overrightarrow{E}\cdot d\overrightarrow{l}=-\int_S \frac{\partial\overrightarrow{B}}{\partial t}\cdot d\overrightarrow{s}$$
閉曲線Cは導線でできた回路を考えてもいいし、空間内のてきとうな任意の閉曲線を考えても良い事になります。導線の回路とは無関係に閉曲線を考えた場合でも、磁場の時間変動(および磁束の時間変動)があるなら起電力に相当する電位差は発生していると見るわけです。
回路として導体でできたものを指定しなくても閉曲線として形状さえ指定すればよいという意味では、確かに物理的には「より一般的な式」であるという事は言えそうです。
空間中に導線の回路ではなくてきとうな閉曲線を考える時には、
その空間というのが空気などの電気的に絶縁性の高い物質中であるか、あるいは真空中という事を想定するなら「電位差(=電圧)は発生していても電流は生じない」事になります。(電位が0でない場所には「電場」は発生しています。)
その事は回路論においての電圧と電流の違いという意味でも重要ですし、電磁波が絶縁物中や真空中であっても伝わって進行していくという点でも大事であると思われます。
ただし絶縁物中や真空中で電流は基本的に発生しないという事は、敢えて「誘導起電力」を考える必然性も無い事も意味すると言えます。そのため、そのような場合には電場と磁場の関係で表したほうが良いという捉え方もできそうです。
法則の微分形
電場と磁場の関係で表した電磁誘導の法則の積分形にストークスの定理を適用すると、法則の微分形を得る事ができます。
ストークスの定理を適用するのは、電場のほうの項です。それが循環(周回の接線線積分)の形になっているので、「電場の回転」の法線面積分として書けます。
$$\oint_C\overrightarrow{E}\cdot d\overrightarrow{l}=\int_{S_0}\mathrm{rot}\overrightarrow{E}\cdot d\overrightarrow{s}$$
開曲面をS0としていますがこれは磁場のほうに対する開曲面と同じである必然性がないので予めそう書いただけであり、本質的にはあまり関係ありません。
$$電磁誘導の法則により\oint_C\overrightarrow{E}\cdot d\overrightarrow{l}=-\int_S \frac{\partial\overrightarrow{B}}{\partial t}\cdot d\overrightarrow{s}であるから$$
$$\int_{S_0}\mathrm{rot}\overrightarrow{E}\cdot d\overrightarrow{s}=-\int_S \frac{\partial\overrightarrow{B}}{\partial t}\cdot d\overrightarrow{s}$$
開曲面S0とSは任意にとれるので、式が成立するには被積分関数が同一でなければなりません。
よって、電磁誘導の法則の微分形が成立する事になります。
これは他のマクスウェル方程式の積分形から微分形への変形の時と同じやり方です。
$$\mathrm{rot}\overrightarrow{E}=-\frac{\partial\overrightarrow{B}}{\partial t}$$ ナブラで書くと次のようになります。 $$\nabla\times\overrightarrow{E}=-\frac{\partial\overrightarrow{B}}{\partial t}$$ この式の形は、マクスウェル方程式の中で言うとアンペールの法則と対になっています。
電磁誘導の法則の微分形は、
磁場の直接的な時間変化と「電場の回転」を関連付ける式です。
少し妙な結果にも思えるかもしれませんが、この微分形の式は物理的には「局所的には磁場の時間変化により電場の渦ができ、回路全体では誘導起電力の発生を意味する」という解釈ができます。
「渦」のイメージは微小な領域に対して積分形を考えてみると比較的分かりやすいかもしれません。それを1点で考えて数式で表すとこのような微分形の式になるわけです。
電磁波の式を導出する時にマクスウェル方程式を組み合わせる時には、基本的に微分形のほうの式を使います。電磁誘導の法則と組み合わせるのはアンペールの法則の微分形です。
時間変動しない磁場中で回路が動く時の法則の形
ところで各位置における磁場が時間的に一定である時に、回路自体を動かしても「回路を通過する磁束」は変化する事になります。(磁場の分布と運動の仕方によっては変化しない事もありますが、一般的に言えば変化をします。)
実際、そのような場合でも電磁誘導は起きます。ただし、その時に電磁誘導の積分形の見た目が違った形で書かれる事があります。
それは接線線積分で書かれる事になりますが、上述の電磁誘導の法則の積分形をストークスの定理等を使って変換したものとは異なります。
時間変動しない磁場中で閉曲線Cを作る回路が運動する時に、
回路の各位置の速度ベクトル(位置の時間変化)を\(\overrightarrow{v}\)とすると
$$V_e=\oint_C \left(\overrightarrow{v}\times\overrightarrow{B}\right)\cdot d\overrightarrow{l}$$
$$=-\oint_C \overrightarrow{B}\cdot\left(\overrightarrow{v}\times d\overrightarrow{l}\right)$$
ここで言う回路の運動とは直線運動でも曲線運動でも良くて(瞬間の位置の変化=速度を考えているので)、回転運動も含みます。また、理論的には閉曲線の形状自体が微小変化する場合も含めて成立する式になっています。
式の1段目から2段目の変形は外積ベクトルの公式によります。
2段目の式は法線面積分としても捉える事ができます。ただし実質的にはそれを閉曲線の周に沿ってだけ考えれば十分であるという意味です。
この法則の形は回路が動く場合に必ず適用しないといけないかというと実はそうではなく、磁束の変化を直接計算できるならそっちで考えたほうが早い場合もあります。
例えば交流の起電力を発生させるために回路を回転させる場合などは上記の式で考える事もできますが、最初から磁束を計算したほうが早いです。
(実際の発電機では、回路を回転させるタイプと磁場を発生させる電磁石部分等を回転させるタイプの両方が存在して使い分けられています。)
電磁誘導の法則の積分形の元の形に即して言えば考え方自体は固定された回路において磁場が時間変動する時と同じで、回路を周・外縁とする開曲面の磁束の変化を計算していると見る事ができます。
回路を閉曲線Cとして、それを外縁とする開曲面Sを考えます。
回路が移動あるいは変形すると、そもそもの閉曲線が変わるので開曲面に対する磁束も変化します。(平行移動や回転で開曲面の形状を変えていなくても。)
1つの閉曲線Cに対しては開曲面Sは任意に選べるので、なるべく大きくならないものを選びます。例えば閉曲線の各点を直線で結ぶ事で形成される曲面などです。
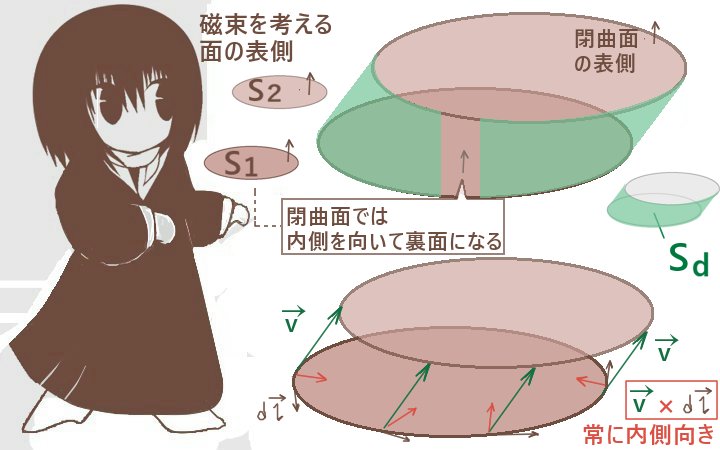
最初に存在する閉曲面S1と、移動後の閉曲面S2を考えて、
それと移動の軌跡で作られる側面の閉曲面Sdも考えます。
次に、速度ベクトルがS1の表面とのなす角が180°以下の時を見てみます。これは速度ベクトルがS1の表面側を向いている状況です。
任意の時刻で静磁場に関するガウスの法則が成立しているとすれば、
閉曲面全体での磁場の法線面積分(=磁束)の合計は0です。
(この事は、電磁誘導の積分形のところで触れた「磁束は1つの閉曲線を外縁として共有している条件のもと任意の開曲面で考えても同じ値になる」という話と同じです。)
その内訳を見ると、最初のS1の表面が「閉曲面の裏面」になる事に由来してS1に対する磁束Φ1とS2に対する磁束Φ2が互いに異符号で存在します。それと軌跡で作られた側面Sdにおける速度ベクトルと接線ベクトルの外積が閉曲線の内側を向いています。
するとΦ2-Φ1-Φd=0 ⇔ Φ2-Φ1=Φd です。
非常に短い時間では、Φdは「速度ベクトル(どの位置でも同じ)と接線ベクトルが作る平行四辺形」を面積に持つ面積要素ベクトルと、磁場との内積を考えた法線面積分です。
しかしこの時の面積要素ベクトルは「速度ベクトルと接線ベクトルの外積ベクトル」に等しく、それを閉曲線C(最初の位置での閉曲線)において周回ですればよい事になります。上記の式で言う2段目の形です。その式をさらにベクトルの外積の公式で変形すると上記の1段目の形が得られます。
$$移動の軌跡で作られる面の磁束\Phi_d=\int_{S2} \overrightarrow{B}\cdot d\overrightarrow{s}=-\oint_C \overrightarrow{B}\cdot\left(\overrightarrow{v}\times d\overrightarrow{l}\right)$$
$$=\oint_C \left(\overrightarrow{v}\times\overrightarrow{B}\right)\cdot d\overrightarrow{l}$$
曲線の一部だけが移動すると考えれば、
回路の形状が微小に変化する場合にも同様に考える事ができます。
次に、S1の表面と速度ベクトルのなす角が180°を超える時、つまり速度ベクトルがS1の裏面側に伸びている状況を考えます。この時は、閉曲面を考える事で表が裏に転じるのはS2のほうになります。さらに、速度ベクトルと接線ベクトルの外積は今度は閉曲面の外側(=表側)を向くようになります。
従ってその場合はΦ1-Φ2+Φd=0となり、
Φ1-Φ2=-Φd ⇔ Φ2-Φ1=Φd となって
先ほどと同じ関係式になったので同様に考える事ができます。
この式は物理的には単位電荷が受ける仕事の変化という観点からも見れます
すなわち、導線中に電荷を持った自由電子があるとしてそれを動かす事になるので生じる電磁力(ローレンツの力)が1[C]あたりの電気量で見ると\(\overrightarrow{v}\times\overrightarrow{B}\) となりますが、この力自体は電荷の速度に垂直に生じるので「生じた電磁力がする仕事はゼロ」です。
しかし実際は、何らかの外力で導線の回路を動かした事による仕事はゼロではありません。(導線の質量を考えた通常の力学的な仕事を抜きにして。)
ここで、電磁誘導によって起電力と電流が回路に生じるとすると、その誘導起電力に由来する電流に働く電磁力\(Id\overrightarrow{l}\times\overrightarrow{B}\) が生じます。
(これは電流を電荷の電気量とその速度に分けて、大きさはQv=Idl で回路の接線ベクトルと電荷の速度ベクトルが等しいと考える事によります。)
この電磁誘導に由来する電磁力は、回路の移動を妨げる方向に働きます。
言い換えると、現に回路を動かせたとすれば電磁力に逆らって外力が仕事をした事になり、その仕事が電気エネルギーに変換されたと見る事ができます。
しかし外力と電磁誘導による電磁力は方向は一般的に一致しないので
外力が「単位時間あたりに電磁力に逆らってした仕事」(つまり仕事率)は内積で考えると
\(-\left(Id\overrightarrow{l}\times\overrightarrow{B}\right)\cdot\overrightarrow{v}=I\left(\overrightarrow{v}\times\overrightarrow{B}\right)\cdot d\overrightarrow{l}\)
右辺は左辺を変形したもので、誘電起電力を外積で表した式の微小量にに電流を乗じたものです。
また電流と電圧を乗した量は実は「電力」であって、電気的な「仕事率」の事です。
積分を行うと両辺共に回路全体での「仕事率」です。(左辺は外力、右辺は電荷によるもの。)
$$-\oint_C\left(Id\overrightarrow{l}\times\overrightarrow{B}\right)\cdot\overrightarrow{v}=I\oint_C\left(\overrightarrow{v}\times\overrightarrow{B}\right)\cdot d\overrightarrow{l}$$
つまり電流も含めて考えると
「外力が電磁力に逆らって行う仕事率」=「誘電起電力が消費できる電力」
という関係式ができます。
磁場の時間変動がある時と時間変動がない磁場中を回路が動く時とでは、結果は同じでも物理的に誘電起電力の発生の機構が違うという見方と、回路の速度は相対的なものである事も含めて本質的にも同じものであるという見方の両方が存在しているようです。
自己インダクタンスと逆起電力
「1つの回路による電流による磁場の変化が、もう1つの回路に誘導起電力を発生させる」という理論をよく考えてみると、磁場を生じている元の回路を通過する磁場も変化しているはずではないのか?と思えるかもしれません。
そして実はそれは正しくて、一般的に電気回路は
「それ自身に発生している電流による磁場の変化があった時」
にはそれに由来する誘導起電力が発生するのです。
そしてその部類の誘電起電力は特に逆起電力と呼ばれます。
それは直流回路で電源を入れた時などは無視できる大きさですが、交流電気回路では考慮に入れる必要があります。特にコイルがある場合には基本的に無視する事はできない事が多いです。
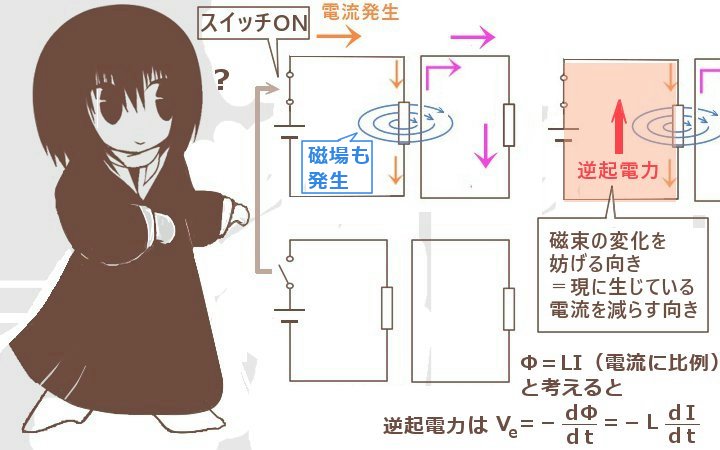
電磁誘導の法則を思い返してみると、磁束の変化を妨げるような向きに誘導起電力が発生するのでした。
つまり、回路の電流がその回路自体に対して及ぼす誘導起電力はまさに「磁場の発生源である電流を減らそうとする向き」に発生します。それは一般的に電源の起電力によってかかる電圧と逆向きであるので「逆起電力」と呼ぶわけです。
実験によって(あるいはアンペールの法則やビオ・サバールの法則から)直線電流によって生じる磁場は電流の大きさに比例します。これは交流電流のように電流が時間変化する場合でも、各時刻で考えると同じ事が言えます。
※アンペールの法則で考える変位電流の影響については、コンデンサーにおける場合などは考える意味がありますがここでの考察のようにコイルなどでは無視できる大きさであるとします。
そこで主に逆起電力を考える場合に特に多く使う考え方として、
比例定数Lを使って磁束をΦ=L I と表現する事が多くあります。
この比例定数Lを、考えている回路の自己インダクタンスと呼びます。
この形の磁束の式を使って逆起電力を表す場合の電磁誘導の法則の式を書くと、
Ve=-(dΦ/dt)=-L (dI/dt)となります。
その形の式は、電気回路に限定した議論のように空間的な電場や磁場のベクトルを考えなくてもよい場合によく使われます。回路で考えている場合の電流は時間に依存する事はあっても、空間的な位置座標には依存しません。
電気回路中において、誘電起電力として逆起電力を表す場合には
比例定数である自己インダクタンスLを使って次のように書く事ができます。
$$\Phi=LI\hspace{5pt}と電磁誘導の法則を組み合わせる事で、$$
$$V_e=-\frac{d\Phi}{dt}=-L\frac{dI}{dt}$$
ここでのマイナス符号は、回路における電流や電圧の「2方向の向き」を表すものです。
電流の方向と逆向きに逆起電力が発生する事を表します。
この電流や電圧の向きはベクトル的な空間的な電流等の向きにも対応していますが、回路だけを考えるならベクトルとして考えなくても同じ形の式が使えます。
微分については「電位回路中の電流」という条件のもとでは電流は空間的な位置座標の関数ではなく、交流回路において時間のみの関数と考える事がでます。そのため、微分は1変数の微分として考えれば十分です。
他回路に対しても同様に考える時には「相互インダクタンス」を考える時もあります。
ただし、考えているのが1つの回路である事が明確な時には
自己インダクタンスを単に「インダクタンス」と言う事も多くあります。
(「自己」と「相互」をまとめて指す意味でインダクタンスとも言います。)
また、無視できない大きさの自己インダクタンスを持つコイルのような部分を回路素子とみなす時には、それをインダクタと呼ぶことがあります。
自己インダクタンスを使った考え方は回路論以外で使ってはいけないわけでは無いですが、
基本的に「電流が作っている磁場が、その電流が生じている回路に及ぼす誘電起電力(=逆起電力)」
を考えているので必然的に電気回路で使う事が多くなるわけです。
ここで、回路にV sin(ωt)で表される交流電源があって、回路素子としては無視できないインダクタンスを持つコイルだけがある状況を考えてみます。
(全ての導線にもコイルにも抵抗成分は必ずありますが、ここでは簡単のためにそれらは無視できる大きさとして考えます。)
すると、キルヒホッフの法則(回路の電圧降下の合計は起電力に等しいというもの)を考えると
「電源の起電力=逆起電力の大きさ」という事になってV sin(ωt)=L (dI/dt)です。
(向きまで含めて考えれば電源の起電力とここでの逆起電力は符号が異なります。)
このtに関する微分方程式は比較的簡単に解く事ができます。
任意定数が0になるように初期条件を考えると、I=-{1/(Lω)}cos(ωt) となります。
【合成関数の微分を考えて(d/dt){cos(ωt)}=-ωsin(ωt)となる事に注意。】
-cos(ωt)=-sin(π/2-ωt)=sin(ωt-π/2)でもあるので、
コイルの端子間電圧(ここでは電源電圧に等しい)V sin(ωt)に対して
コイルに生じている電流は「位相がπ/2遅れている」という表現もされます。これは交流回路論においては割と重要です。
その条件のもとでは電源の起電力と回路の電流の最大値の絶対値だけで関係を見ると
|V|=|I|/(Lω)となっています。
(交流回路では電圧や電流の最大値を2の平方根で割った「実効値」が使われますが、実効値で考えても同じ関係が成立します。)これは交流回路を分析する時に実は便利な関係です。
そこで、角速度(回路論や通信工学などでは角周波数とも言います)も含めたLωという値を改めて誘導リアクタンスと呼ぶ事もあります。
この誘導リアクタンスを使用する場合には、位相の変化も含めて考える必要がある事も多いです。
実はコンデンサーについても同様の考察ができます。一般的に、コイルに対するLωという量と、コンデンサの容量を使って表される1/(Cω)という量を共にまとめて「リアクタンス」と呼び、さらに抵抗成分と合わせたものをインピーダンスと呼びます。
使われ方:1発電機における電磁誘導
電磁誘導を利用して発電を行う発電機にはいくつか種類がありますが、
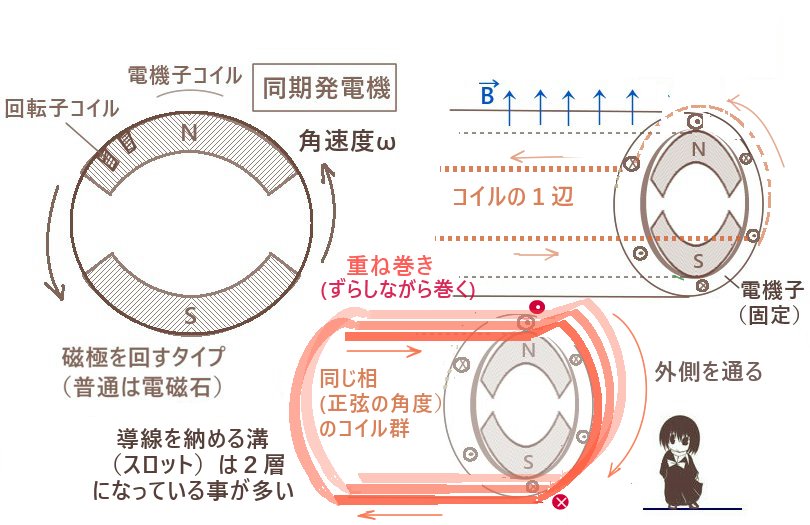
実はいずれも電動機(モーター)と対になった分類になっています。発電所で従来から使われてきた発電機で多いものは同期発電機(synchronous generator)と呼ばれます。以下、積分などの計算はありませんがいわゆる電気機器・電気機械の理論独特の多少込み入ったな話も一部含まれます。
- 同期発電機:発電所で多く使われてきた発電機。火力発電などでは一般的に巨大。
- 直流発電機:交流ではなく直流の電源として使える発電機。
- 誘導発電機:誘導電動機という種類の電動機を発電機として使ったもの。やや稀なタイプ。
原理的には交流の電源を作るには磁場を回転させてもよいし,
磁場を固定して回路の一部であるコイルのほうを回してもよいのですが、火力発電に使われるような大型の同期発電機では磁場を発生させる電磁石(以下、「磁極」と呼びます)のほうをタービンの軸に接続して回転させます。
(規格では3300[V], 6600[V]や、それを超えるものなど)
しかも発電所の発電機では、送電の都合上の理由等から位相(正弦波の角度)が異なる3つの交流起電力を発生させる事が多いです。その方式の電線路は三相三線式と呼ばれます。
そしてそのようなものを高速で回すような事はできればしたくないといった事情や、電磁石側のほうが機械的に丈夫に作りやすいといった理由により、容量の大きい同期発電機では多くの場合に電磁石のほうを回転させます。電磁石を作るほうの電源は一般的に低圧です。
電磁誘導の法則を使って発電機という「機械」を作って運用するとなると、電気と磁気に関する事が特に重要ではありますがその他の力学的・機械的な事も多く関わってきます。例えば電磁石を回転させるタイプのものでは、遠心力を抑えるために直径はなるべく小さく抑えて長い円筒形の形状にするといった事です。
また、発電を行っていると「損失としての熱」も多く発生するので冷却という事も考慮に入れる必要が出てきます。
この場合、誘電起電力を発生させるコイルは回転する磁極を囲むようにして固定されます。
磁極は通常の磁石のようにNとSに相当する部分が対になりますが、この対を複数設置して同時回転させる事もできます。火力発電では2極(つまりNとSの1対だけ)の事が多く、小規模の水力発電などでは多くの極(例えば多いものでは48極)などが使われる傾向があります。
発生する起電力の計算に使うのは、
電磁誘導の法則において「磁束の時間変化」を直接使うパターンです。
磁極を回転させる時にはコイル面に対する磁場の垂直成分が理想的には時間を変数として正弦関数と嬉しいのですが、実はコイルの配置などを工夫しないと歪んだ台形のような波形になってしまいます。(周期関数を正弦波の和で表す考え方だと「高調波」成分が多くなる事を意味します。)
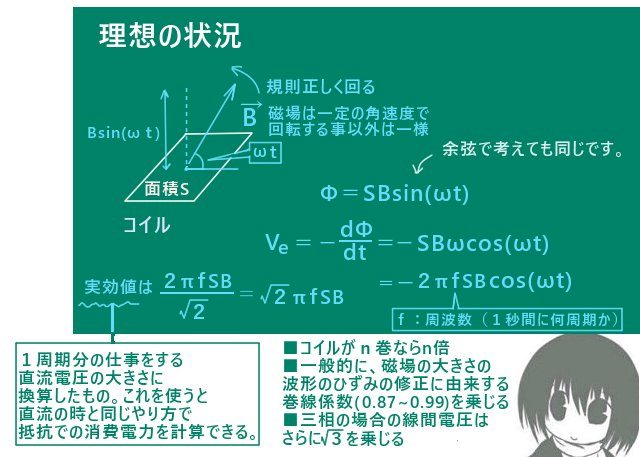
ここではそのような工夫が既にされているとして、誘導起電力を発生させるコイルにおける磁場の波形が正弦波に近似できるものとします。また、磁束を考える面は長方形状のコイルの平らな面であるとして、その面積をSとします。
さてそのような時には考察は比較的簡単で、
コイルの面の面積要素ベクトルと磁場のなす角度が回転磁極の角速度ωと時間tの積ωtで表せる事になります。
今、磁場ベクトルの大きさが一定でBであるとします。
コイル面に対する垂直成分B0が正弦波で表されるとすると
B0=Bsin(ωt)で、ωt=π/2の時に最大値です。
(磁場とコイル面の面積要素ベクトルとのなす角θを使えばB0=Bcosθであり、
位置関係としてはθ+ωt=π/2です。)
よってこの時のコイル1巻き分の磁束はΦ=SBsin(ωt)で、1巻きのコイルに対する誘電起電力は
Ve=-(dΦ/dt)=-ωSBcos(ωt)=ωSBsin(π/2-ωt)です。
自己インダクタンスを使った計算時のように合成関数の微分になります。
$$合成関数の微分である事に注意して、V_e=-\frac{d\Phi}{dt}=-\frac{d}{dt}\left\{SB\sin (\omega t)\right\}=-\omega SB\cos (\omega t)$$
速度ではなく周波数f[Hz] で考えるならω=2πfなのでVe=-2πfSBcos(ωt)です。
実効値で考えるのであれば最大値(つまり正弦または余弦が1の時)の絶対値を\(\sqrt{2}\)で割って
V =\(\sqrt{2}\pi\)fSB です。
(SもBも定数であるのでまとめて\(\phi\)=SBとおいてしまう事もあります。)
以上の結果はコイル1巻きに対してなので、n回巻かれていればn倍になります。
その他、導線の結線方法やコイルの巻き方に由来して所定の値や係数が乗じられます。
ただし発電機の誘電起電力は高ければ高いほど良いというものでも無いので、用途に応じて所定の電圧の電源になるように構造が決定されています。
- 磁場の大きさの波形を正弦波に近付けるために1箇所にコイルの巻きを集中させない方式(分布巻、短節巻等)を使った場合は誘電起電力が理論値より少し減るので巻線係数kを乗じます。
kは基本的におおよそ0.87~1未満の値です。
さらに細かく見るとこの巻線係数は別の2つの係数の積です。 - 3つの正弦波の位相が互いに120°ずれた「三相三線」の線路として出力する場合は、
2本の導線の「線間電圧」は1相で考えた場合の\(\sqrt{3}\)倍になります。
2極の同期発電機において周波数がf、1つのコイルの巻き数がn、巻き線係数がkであり
コイル面を通過する磁束の最大値\(\phi\)=BSが一定値である時には、
1相ごとの誘導起電力の実効値は次のように表されます。
$$V_e=\sqrt{2}\pi knf\phi\hspace{3pt}≒\hspace{3pt}4.44knf\phi$$
比例定数の一部を「4.44」という数字でも書いたのはちょっとしたオマケで、
「たまたまそのように特徴的で覚えやすい値である」という意味です。
この式の導出方法は他にもありますが、
ここでは電磁誘導の法則に即して一番簡単と思われる方法での導出を説明しました。
使われ方2:変圧器における電磁誘導
変圧器は変電所に設置されている装置であり、電柱の上にも設置されています。
2つの電気回路を接続し、それぞれの接続部分にコイルがあります。電柱に張り巡らされた電線の2線間の電圧は高圧の6600[V] であり、それを家庭で使う100Vに下げます(降圧)。逆に、発電所から鉄塔の送電線に向けては特別高圧の範囲の1万~50万[V] にまで電圧を上げます(昇圧)。
変圧器の原理は発電機と同じく電磁誘導であり、交流回路においてのみ機能します。理論的には前述の逆起電力の考え方が重要な部分の1つでもありますが、変圧に関する結果の式は非常に簡単で2つのコイルの電圧の比は「コイルの巻き数の比に等しい」というものです。
変圧器で接続された2つの電気回路のうち電源側のほうの量である事を指して「1次」と言い、もう片方の回路の量である事を指して「2次」と呼ぶ事があります。
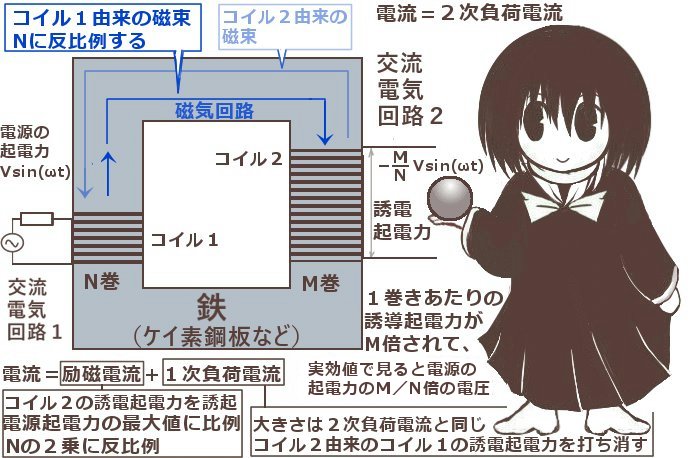
今、変圧器の1次側のコイルの巻き数がNで2次側のコイルの巻き数がMである時、1次側のコイルの端子間電圧と2次側の端子間電圧の実効値は次式で表されます。
$$\frac{E_2}{E_1}=\frac{M}{N}$$
これはつまり、例えば電圧を2倍にしたいなら2次側のコイルの巻き数を1次側の巻き数の2倍にすればよいし、逆に降圧を行うのであれば2次側よりも1次側の巻き数を多くすれば良い事になります。
結果の式は簡単ですが、導出する時には実は少し注意が必要な点もいくつかあります。
以下、導出の概略について説明します。
1次側のコイルによる電誘誘導によって2次側の回路に誘導起電力が生じるわけですが、この時に実は2次側のコイルによる磁束の変化が1次側に逆に影響を及ぼします。
ただし1次側に変化があるのは実は電圧ではなく電流のほうで、2次側からの電磁誘導に由来する電流が逆起電力を発生させて結果的に1次側の電圧の変化を打ち消す仕組みになっています。
そのため、変圧器で2つの回路を接続した時には1次側には2種類の電流があると考えます。「励磁電流」はであり、「1次負荷電流」は2次側のコイルからの電磁誘導に由来する電流です。しかし大きさ的には一般的に後者のほうが大きくなります。
- 「励磁電流」:2次側の回路に誘導起電力を発生させる電流。大きさ的には小さい。
- 「1次負荷電流」:2次側のコイルからの電磁誘導に由来する電流。
ただし逆起電力によって、結果的に1次側のコイルの端子間電圧に基本的に影響を与えない。
1次側の励磁電流によって、1次側のコイルには巻き数Nに比例する磁場が発生します。
そこで、この励磁電流による磁束は励磁電流の大きさと1次コイルの巻き数に比例するとして
Φ0=kNI とおけます。
ビオ・サバールの法則を使ってコイルで発生する磁場が「巻き数と電流に比例する事」を比較的簡単に(と言っても割と面倒ですが)導出できるのは、円筒に導線を均一に巻いた模式的なソレノイドにおいてです。
他方で、実際の変圧器の多くは断面が四角形です。
しかし近似的にはソレノイドのように考える事ができます。
ここで、自己インダクタンスLの定義は
「電流が発生させた磁束について」Φ=LIとなるような定数の事でしたが、
電流がコイルの1つ1つの輪に作用して逆起電力を発生させている事を考えると
実はこの場合の磁束は「Φ0のN個分の合計」として考える必要があります。
そのために1次コイルのに対して励磁電流が発生させた磁束の合計は Φ=kN2I であり、
自己インダクタンスはL1=kN2となるのです。
この時に回路の抵抗成分は小さいとすると、逆起電力V1の大きさは電源電圧とほぼ同じになります。(向きは互いに逆です。)
電源の起電力をVsin(ωt)とすると、
Vsin(ωt)=-L1(dI/dt)により(あるいはリアクタンスL1ωを使って)
励磁電流は I=-{Vcos(ωt)}/(L1ω)=-V{cos(ωt)}/(kN2ω)です。
つまり、少し妙な感じもするかもしれませんが
「励磁電流の大きさは1次コイルの巻き数の2乗に反比例する」というわけです。
【逆起電力は、ここでは大きさが電源の起電力に等しく向きが逆でV1=-Vsin(ωt)です。】
励磁電流の大きさは変圧器回路の1次コイルの巻き数の2乗に反比例します。
- 1次コイルの自己インダクタンスを計算するとN2(巻き数の2乗)に比例する。
- 抵抗分が少ないとしてキルヒホッフの法則(ここではオームの法則でも同じ)から励磁電流を計算すると、励磁電流の大きさは1次コイルの自己インダクタンスに反比例する
- よって、励磁電流の大きさはN2に反比例する事になります。
ここで改めて1次コイルが近似的にソレノイド同様の磁場を作ると考えると、先ほどと同じように考えてΦ0=kNI=-V{cos(ωt)}/(Nω)の磁束が発生しますが今度はこれは1次コイルではなく2次コイルのほうに作用している状況を考えます。
2次コイルでの誘電起電力V2は電磁誘導の法則により -(dΦ/dt)を計算する式で考えます。
1巻きではNに反比例し、2次コイルでM巻きの導線の輪があるのでM倍します。
つまり、Φ0=-V{cos(ωt)}/(Nω)をtで微分して符号を変えてからM倍する事によって、
V2=-M(dΦ0/dt)=-VM{sin(ωt)}/Nです。
(結果的にωは式から無くなります。)
よって、V1≒-VのもとでV2/V1={-VM{sin(ωt)}/N}/{-V{sin(ωt)}=M/Nとなります。
(実効値をE1およびE2として、E2/E1で考えたとしても同じようにE2/E1=M/Nとなります。)
以上の事は、交流回路における複素数法(交流の電流と電圧は複素数として直流回路同様に計算しても正しい結果を得る)を使うと少しだけ計算は見やすくなります。
ところで磁気的に接続されていても、電気的には接続されていない2つの回路間の電流や電圧についてプラスマイナスの符号での「向き」を比べる意味があるのかという話にもなりますが、これは正弦波の位相で考えると比較的分かりやすいかもしれません。
マイナス符号が付いているという事は正弦波では
「位相が180°(弧度法でπ)ずれている波形」としても表せます。
そのため、交流回路においては電気的には直接接続されていない2つの回路間でも位相の観点からはプラスマイナスの符号の関係も意味を持ち得る事になります。ある時刻で1次側の何らかの量の位相がθの時に、2次側のある量の位相はθ-πで表されるといった事が分かるからです。
1次側・2次側単独で見た場合はプラスマイナスの符号は通常通りの「向き」として見れます。