複素数の指数関数表示について説明します。
これは「オイラーの公式」とか「オイラーの式」とも呼ばれますが、じつは同じ名前・似た名前で全く別の公式や定理が複数存在します。大変紛らわしく、使用する都度に「複素数に関する・・」「実関数の解析学における・・」「幾何学での・・」このように断り書きをつけるのは大変不便なので、
このサイトではeiθを表す語としては「複素数の指数関数表示」という表現を採用します。
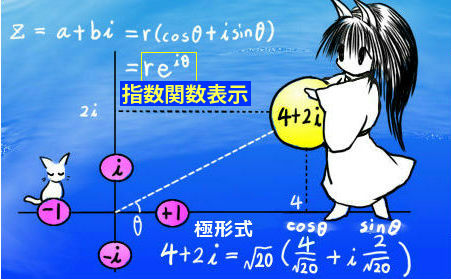
複素数の指数関数表示とは次のようなものです。
複素数の極形式表示を指数関数の形で書く事ができ、次のように定義します。 $$e^{i\theta}=\cos\theta +i\sin\theta$$ このeは自然対数の底です。eiθを exp(iθ)と書く事もあります。これは実数範囲の指数関数での表現と同じです。(exponential の略)
こういう形なので、eiθの絶対値は1になります。
$$|e^{i\theta}|=|\cos\theta +i\sin\theta|=1$$
さて、このように「指数関数」で書くからには指数関数としての規則を満たしているのかというと、きちんと満たしています。これらの性質、特に微分の演算は表記を簡易にするので便利です。
- 積の演算:eiθeiω=ei(θ+ω)
eiθeiω=(cosθ+isinθ)(cosω+isinω)
=cos(θ+ω)+isin(θ+ω) 【ドモアブルの定理より】
=ei(θ+ω) - 微分:(d/dθ)eiθ=ieiθ 【合成関数の微分使用】
(d/dθ)eiθ=(d/dθ)(cosθ+isinθ)
=-sinθ+icosθ=i(cosθ+isinθ)
=ieiθ
見ての通り、この指数関数表示は三角関数の性質に直接的に関わるものです。
(ドモアブルの定理の成立根拠は三角関数の加法定理。)
実際、一見唐突にも見えるこの「指数関数の定義域の拡張」は三角関数をもとに考えられたものです。
「三角関数と指数関数では全然違うではないか?」という話ですが、それらをテイラー展開すると似た形をしているのです。(微分の性質も似ている事に注意:eの指数関数は微分に関して1回周期、三角関数は4回周期でもとの関数に戻ります。さらに正弦関数と余弦関数は微分により符号を変えながら互いに互いの導関数に変化します。)
特にマクローリン展開(x=0でのテイラー展開)の形にすると形は似てきます。
$$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots$$
$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$$
$$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots$$
ここで、正弦関数の場合は「偶数項」が抜けていますが、余弦関数を見るとちょうどそれを補うように項が並んでいるのです。(正弦関数を微分すると余弦関数になる事に対応します。)これを合わせると、ちょうど指数関数のほうで使っている項が並ぶ事になります。
しかしそれでも符号が変わっている箇所は対応しないという話になりますが、ここで指数関数exに「ix」を「形式的に」代入してみるという工夫をしてみます。
$$e^{ix}=1+ix-\frac{x^2}{2!}-i\frac{x^3}{3!}+\frac{x^4}{4!}+i\frac{x^5}{5!}-\frac{x^6}{6!}+\cdots$$
これをよく注意して見ると、次の規則があります。
- 虚数単位iは奇数項にのみつき、偶数項にはつかない。
- 奇数項と偶数項に分けてみると、それぞれが1項ごとにプラスマイナスの符号が反転する。
そこで、奇数項と偶数項に分けて式を整理すると次のようになります。
$$e^{ix}=\left(1+\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots\right)+i\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots\right)$$
$$=\cos x +i\sin x $$
このように「導出」できるわけですが、基本的には複素数の指数関数表示は上記のように「定義」するものになります。複素数の範囲に定義域を拡張する時には上記のようにすると定義するわけです。
しかしそういう事を言うと、定義域の拡張の際に「別のやり方」もあるのではないかという問題も起きます。上記のように定義する必然性がないのではないか、という事にもなります。
この件について複素関数論においては、「正則関数」になるように定義域を拡張する場合には上記のようにeiθ=cosθ+isinθ のようにするしかない、という位置付けになります。(その際にも重要になるのはじつはテイラー展開です。)