三平方の定理は平面の直角三角形の辺の長さに関して成立する関係式です。(曲面に対して拡張したものも存在します。)別名をピタゴラスの定理とも言います。
目次:
中学で教わる数学公式の中でも重要度が高いものの1つだと思います。
定理の内容
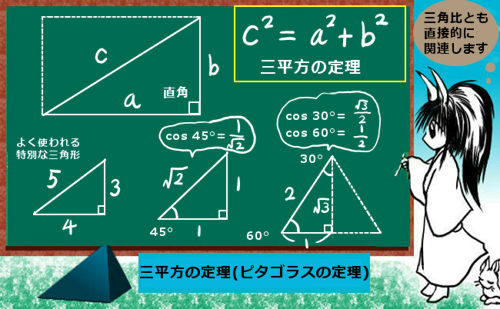
直角三角形の斜辺の長さの2乗は、残りの2つの辺のそれぞれの2乗の合計に等しいというのが三平方の定理の内容です。「平方(つまり2乗)」が3つある事が「三平方」の意味です。
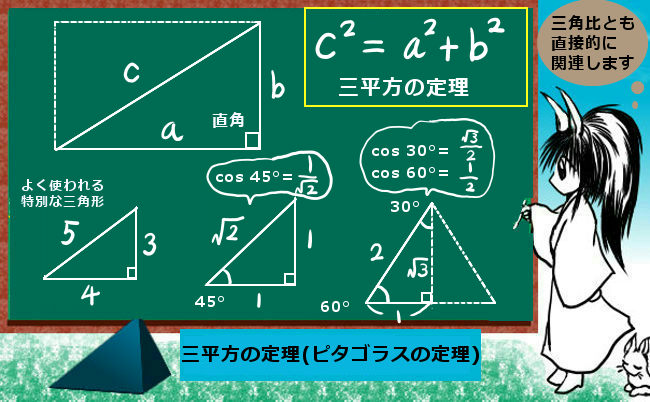
直角三角形の斜辺の長さをc、残りの辺の長さをそれぞれa、bとすると次の関係が必ず成立する:$$c^2=a^2+b^2$$
これは一般の鋭角三角形、鈍角三角形も含めた余弦定理の特別な場合です。
【余弦定理は、普通は高校数学で学習します。】
$$c^2=a^2+b^2 -2ab\cos \theta$$
θ=90°の時 cosθ=0であり、余弦定理は三平方の定理に一致します。
ただし、余弦定理の証明には三平方の定理が必要です。
具体的な適用例としては、直角を挟む2辺がそれぞれ3、4である直角三角形の斜辺の長さは5になります。
32+42=25=52 という計算になるわけです。
また、1つの角度が45°、60°といった特別な三角形の斜辺の長さの計算にも三平方の定理を使います。
1つの角度が45°の場合・・2つの辺の長さがそれぞれ1の時、
12+12=2 より、斜辺の長さは\(\sqrt{2}\)
1つの角度が60°の直角三角形の場合は、2つ合わせると正三角形になる事を組み合わせて、斜辺と1つの辺から、もう1つの辺の長さを三平方の定理で計算するという流れになります。
$$c^2=a^2+b^2\Leftrightarrow b^2=c^2-a^2\hspace{5pt}の関係を使います。$$
斜辺の長さを2とすると、もう1つの辺の長さは1であるので、残る1辺の長さは\(\sqrt{2^2-1^2}=\sqrt{3}\)
ちなみにこれが三角比・三角関数における、角度が特別な時の値の正弦や余弦の意味に直接関連します。
$$ \cos 45°=\frac{1}{\sqrt{2}}$$
$$\cos 60°=\frac{1}{2},\hspace{10pt}\cos 30°=\frac{\sqrt{3}}{2}$$
証明
証明の方法は1つではなく複数ありますがここでは2つ紹介します。
※上記でも触れた余弦定理の証明には三平方の定理が必要なので、余弦定理の特別な場合として三平方の定理が成立するという事は、証明としては使用できないのです。
①三角形の相似関係を使う方法
この方法は、直角三角形の中には別の小さな直角三角形が必ずある事に注目して、三角形の相似関係から辺の長さを計算すると三平方の定理の内容が得られるというものです。
三角形の相似を使う方法は、アインシュタインが12歳ほどの時に自ら証明したと、のちに語ったと言われているものです。これは、彼が「発見」したというよりは、どのように証明ができるのか自ら考え、自力で見出す事ができてとても嬉しかった、というエピソードですね。彼曰く、謙遜してかもしれませんが「苦労」したとのことです。
まず、直角の部分の頂点から、斜辺に向けて垂線を引きます。その垂線の足で斜辺の長さを分割するのです。
図のように長さを変数でおき、三角形の相似関係で式を組み立てます。
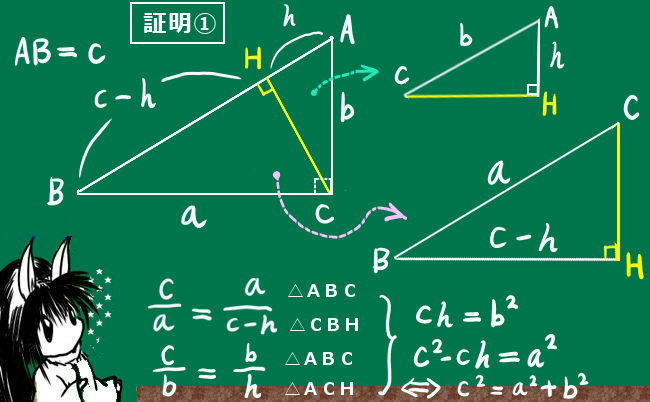
c=(c-h)+h となるように辺ABを分割します。
∠AHC=∠BHC=90°となるようにします。(そのようにできる点Hが必ずAB上に存在。)
この時、もとの三角形と相似関係にある小さな三角形は2つある事がポイントです。
すると、三角形の相似関係により辺同士の長さの比は次のようになります。
$$\frac{c}{a}=\frac{a}{c-h}\Leftrightarrow c^2-ch=a^2$$
$$\frac{c}{b}=\frac{b}{h}\Leftrightarrow ch=b^2$$
$$2式を合わせると、c^2-b^2=a^2\Leftrightarrow c^2=a^2+b^2【証明終り】$$
どの辺がどの辺に対応するか分かりにくい場合には、図のように相似関係が明らかに成立すると分かるように図を描き直して整理すると見やすいと思います。
②三角形の合同関係と面積を使う方法
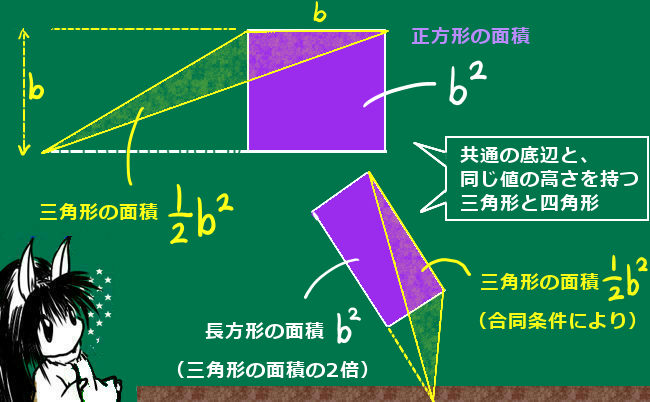
この方法はユークリッドの『原論』における証明方法として古くから知られ、3つの「平方」とは正方形の面積であるという考え方によります。(※「ピタゴラス」によるものではないのです。)
直角三角形の各辺を1辺とする正方形を3つ作り、三角形の合同関係から斜辺の長さの正方形の面積は、残る2つの正方形の面積の合計に確かに等しい事を示せるのです。
補助線を1本引きますが、じつはこれは上記の相似関係で使ったものと同じです。ただしこちらの証明では、補助線は斜辺を突き抜けて正方形のもう1辺にまで伸ばす事になります。
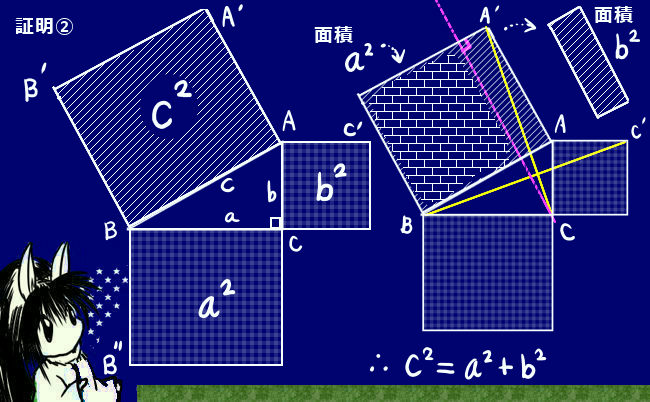
合同関係は、図で言うと△AA’Cと△ABC’について成立します。合同という事は面積も等しい事がポイントで、図をよく見ると、この細長い三角形の面積は正方形の半分、つまりb2÷2です。底辺、高さともに長さはbであることによります。
合同条件は「2辺とそのはさむ角が等しい」です。
図で言うと次のようになります。
AC=AC’ AA’=AB ∠CAA’=∠C’AB=90°+∠BAC となります。
同様に、図の△BB’Cと△BB”Aについても合同関係が成立し、こちらの面積はa2÷2です。
ここで、補助線によって分割される大きな四角形の長方形部分の面積は、細長い三角形の面積の2倍である事に注目します。(底辺と高さの値が三角形のものと等しいため。)
長方形の面積の合計は正方形の面積c2に等しいですから、c2=a2+b2が成立するというわけです。
定理の「逆」も成立する
上記での証明は、正確には次の命題の証明になっています:
三角形の斜辺の長さがc、残りの2辺の長さがa、bのもとで
三角形ABCは直角三角形 ⇒ c2=a2+b2
では逆に、
c2=a2+b2 ⇒ 三角形ABCは直角三角形
という命題は成立するのかというと、じつは成立します。
この証明は次のようにします。(これもユークリッドの方法です。)
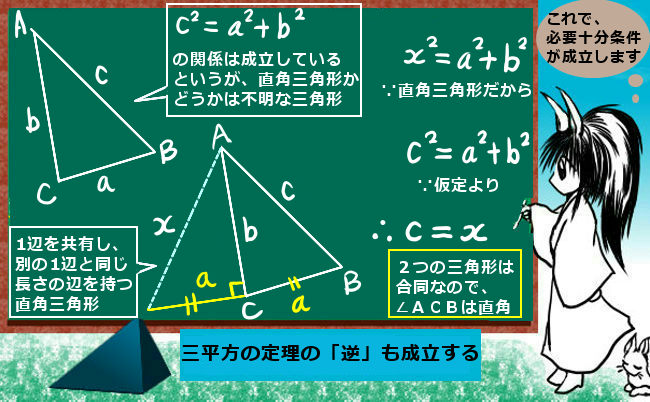
c2=a2+b2 が成立している三角形と1辺を共有する直角三角形を考えます。この直角三角形の1つの辺は、もとの三角形の別の1辺と同じ長さのものを考える事が必ず可能です。
この時点で、最初の三角形と別途に作った直角三角形は、2つの辺の長さが等しいわけです。
ここで、
命題:三角形ABCは直角三角形 ⇒ c2=a2+b2は直角三角形
は上述の証明方法により真であると言えますから、新しく作った直角三角形についてこれを適用できます。
すると、2つの三角形は2辺が等しいですから、辺の長さについて「三平方」の関係がともに成立する条件になるので、残りの1辺の長さも等しくなるのです。
これによって、もとの三角形は新しく作った直角三角形と合同です。(合同条件は『3組の辺の長さがそれぞれ等しい』。)という事は、もとの三角形も直角三角形であるという事です。もちろん、斜辺に対応する角が直角になります。
よって、命題:c2=a2+b2 ⇒ 三角形ABCは直角三角形
も成立しますから、三平方の定理は「必要十分条件」の形という事になるのです。
三角形の斜辺の長さがc、残りの2辺の長さがa、bのもとで
三角形ABCは直角三角形 ⇔ c2=a2+b2
他の分野との関連
上記で三角比および三角関数との関連に少し触れましたが、他の数学的事項や物理学・種々の工学とも密接に関連します。
三平方の定理は様々な場面で「距離」を計算する計算のツールとして使われます。直交座標を考えた時、斜めの線の長さは2点間の距離になります。この時、座標さえ分かっていれば三平方の定理から距離を必ず計算できるというわけです。
この「距離」という考え方はもちろん理論の中だけではなくて現実の距離の計算にも適用できるので、物理学でもじつに頻繁に使用され、また測量のような、より実務的な事項にも間接的に利用されます。
数学の図形的な平面幾何以外の分野でも、ベクトルや複素数の理論において三平方の定理をもとに定義が成されます。ベクトルの「大きさ」や複素数の「絶対値」の考え方自体は、三平方の定理そのものです。
$$\overrightarrow{X}=(x,y)のとき、|\overrightarrow{X}|^2=x^2+y^2$$
$$z=x+iyのとき、|z|^2=x^2+y^2$$
上記で少しアインシュタインに関するエピソードを紹介しましたが、彼の特殊相対性理論の考察においても三平方の定理は使用され、一般相対性理論では平面ではなくて曲面(4次元)において三平方の定理を拡張した考え方の一部が使用されています。なお、平面から曲面に拡張を行ったときには必ずしも「三平方」ではなくなってしまうので、その観点から「ピタゴラスの定理」のほうの名称を優先して使うべきではという考え方をする人もいます。