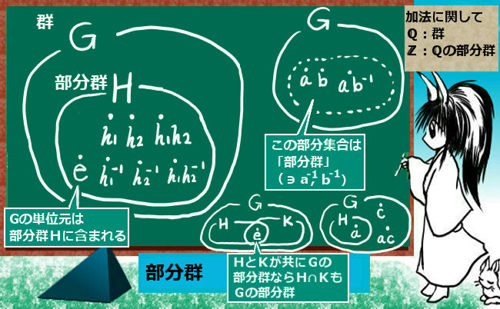
群【ぐん】を作る集合の部分集合で、それ自体でも群を作るものを部分群と言います。
英:部分群 subgroup 正規部分群 normal subgroup
考え方と具体例
簡単な例で言うと、加群としての整数全体の部分集合のうち「偶数である整数の全体(負の数と0含める)」もそれ自体で加法に関して群を作るので部分群であるという事になります。
これに対して、「奇数である整数の全体(負の数含む)」は整数全体の部分集合ではありますが、加法について単位元となるべき0を含まない、奇数+奇数=偶数になる等の理由により加法について群になりません。そのため、加法に関して言えば「部分群では無い」という判定になります。
また、他に重要な例としてはn次の置換全体を表す群(対称群)に対して、n次の偶置換全体を表す群(交代群)も部分群になります。
- 0を除く実数全体に対して、0を除く有理数全体は乗法に関して部分群になる。
【無理数全体は実数全体の部分集合だが部分群にならない】 - 有理数全体に対して、整数全体は加法に関して部分群になる。
- 整数全体に対して集合{2n | nは整数}は加法に関して部分群になる。
【集合{2n+1|nは整数}は整数全体の部分集合だが部分群にならない】 - n次の置換全体Snに対してn次の偶置換全体Anや、
1文字だけ固定してn-1次の置換全体Snー1同様に考えた集合は部分群になる。
【Snの部分群を一般に「置換群」と呼びます。】

このように具体例で見るとそれほど難しいものではないのですが、代数学の群論ではもう少し抽象的なレベルでの部分群についての性質が重要になります。
式での定義と性質
部分群である事の定義を記号で書くと次のようになります。
群Gの部分集合Hが次の2条件をともに満たす時、Hを「部分群」と呼びます。
- a∊Hかつb∊H ⇒ ab∊H
- a∊H ⇒ a-1∊H
Gが群でG⊃Hですから、元同士の積が行える事や逆元の存在自体は前提になっています。
群Gに対してG自身や単位元だけからなる集合{e}も部分群になります。それらを除いた部分群を特に「真部分群」と言う事もあります。
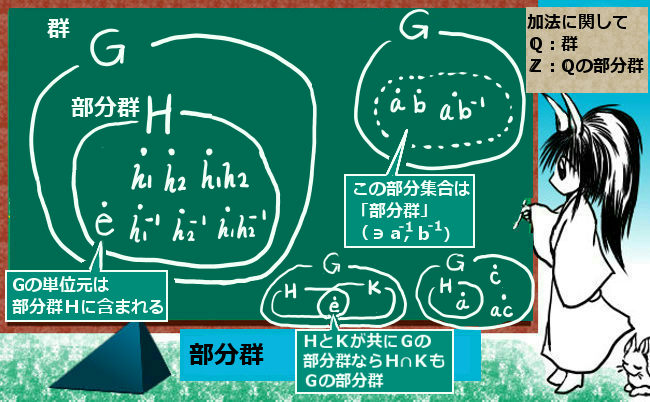
部分群に関する重要な最初の性質として、
「部分群Hが存在する時、Gの単位元は必ずHに含まれている」という事が言えます。
「eが群Gの単位元」⇔「eは部分群Hの単位元」
(GとHとで別々の単位元を持つ事はなく、共通の単位元を必ず持つ。)
【証明】定義の2番目の条件により「a∊H ⇒ a-1∊H」であり、
定義の1番目の条件により「a∊Hかつb∊H ⇒ ab∊H」なので
「a∊Hかつa-1∊H」であるから「aa-1=∊H ⇔ e∊H」と言える事によります。
逆にeがHの単位元であれば、そのeがGの単位元ではないとするとHの外にGの単位元e’ がある事になりますが、先に示した事からそのe’ は部分群Hの単位元でなくてはなりません。しかしこれは、任意の群の単位元は一意性と矛盾します。よってeがHの単位元であればGの単位元でもあります。
さらに、定義から少し計算をすると「部分群である事」を次のように言い換える事もできます。
次の関係が成立します。
「群Gの部分集合HがGの部分群である」⇔「a∊Hかつb∊H ⇒ ab-1∊H」
【証明の中で示されるように、「a∊Hかつb∊H ⇒ ab-1∊H」が成立するならa-1∊Hとb-1∊Hも成立します。ただ、例えばある部分集合が部分群になっている事を示すには「a∊Hかつb∊H ⇒ ab-1∊H」であるかを調べれば十分という事です。】
この必要十分条件の関係は自明ではないので証明が必要です。ただ、理屈自体は非常に単純です。
まず、「群Gの部分集合HがGの部分群である」ならば、
定義から「『a∊Hかつb∊H ⇒ ab∊H』かつ『a∊H ⇒ a-1∊H』」ですから、
b∊Hよりb-1∊Hであり、「a∊Hかつb-1∊H」であるから 「ab-1∊H」となります。
この時「a∊Hかつb∊H ⇒ ab-1∊H」の関係が確かに成立しており、
「群Gの部分集合HがGの部分群である」⇒「a∊Hかつb∊H ⇒ ab-1∊H」が成立します。
次に、「a∊Hかつb∊H ⇒ ab-1∊H」であるとすると、
「a∊Hかつa∊H」【b=aの時に相当】は常に成立するので、aa-1∊H ⇔ e∊Hであり、
「e∊Hかつa∊H」であるからea-1∊H ⇔ a-1∊H となるので、
この時「a∊H ⇒ a-1∊H」が確かに成立しています。
なおかつ、e∊Hが示されているので「e∊Hかつb∊H」も成立し、
aの場合と同様にeb-1∊H ⇔ b-1∊Hとなり、
「a∊Hかつb-1∊H」も成立するのでa(b-1)-1∊H ⇔ ab∊Hも成立します。
つまり「a∊Hかつb∊H ⇒ ab-1∊H」⇒「群Gの部分集合HがGの部分群である」が成立しています。
これらの証明は「確かにそうなるという事の保証」のようなもので、結果のほうが重要です。
部分群についての他の基本的性質としては、次のようなものがあります。
- 群Gに対して2つの異なる部分群HとKがある時、
その共通部分H∩Kも1つの部分群になる。
【Gの単位元はH∩Kに含まれる事になります。】 - 群Gに属するが部分群Hに属しない元c対して、
部分群Hに属する元aとの積acはGに含まれHには含まれない。$$【Gが群、Hがその部分群の時、c\in Gかつc\notin H かつ a\in H\Rightarrow ac\notin H】$$ - 群Gに属するが部分群Hに属しない2つの元bとc対して、
積bcはHに含まれる場合・含まれない場合両方ともあり得る。
【証明】
■1番目の性質:a∊H∩Kかつb∊H∩Kとすると、
a∊Hかつb∊Hなので ab-1∊Hであり、
a∊Kかつb∊Kなので ab-1∊Kであるから、
ab-1はHの元でもあり、同時にKの元でもある、
つまりab-1∊H∩Kとなるので、
部分群であるための必要十分条件により示されます。
■2番目の性質:\(c\in Gかつc\notin H かつ a\in H\) のとき、ac∊Hとすると、
a-1∊Hなのでa-1ac∊H ⇔ c∊H
しかしcはHに含まれないはずだったので、これは矛盾です。
あるいは、c∊Gとa∊Hに対してa-1(ac)=c\(\notin\)Hなので、
c\(\notin\)Hならa-1∊Hであるからac\(\notin\)Hとなる、とも言えます。
ここでの3番目の性質は一体何を言っているのかというと、加群で考えると比較的分かりやすいでしょう。
整数全体に対して3の倍数(0と負の数含む)を考えます。この時に、3n+1や3n+2で表されるものはもちろん3の倍数になりませんが、その和(群論一般で言うとこれが「積」に該当)は3n+3=3(n+1)ですから3の倍数になります。
他方、3n+1で表されるもの同士の和は3n+2の形ですから、3の倍数にはなりません。おおもとの群の元であって部分群の外にあるもの同士の積(加群だと「和」)は、部分群の元になる時もあるし、そうでない事も両方あり得るという事です。
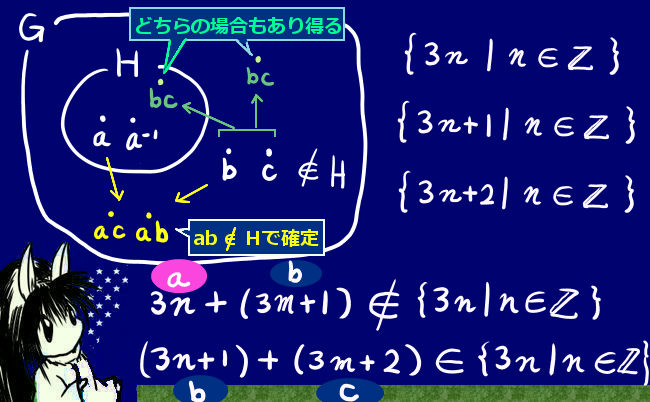
このため、部分群Hの元aとその外にあるおおもとの群Gの元cの積acはHに含まれませんが、さらにその積同士を考えると部分群の中に戻る事もあります。例えばa∊Hのもとでacとc-1aがともにHに含まれない場合でも、その積はacc-1a=aaですからこれはHの元になります。
巡回部分群
群Gがあるとき、a∊Gに対して実数等との時の感覚でaa=a2、aaa=a3、a-1a-1=a-2、a-1a-1a-1=a-3、・・のように書きます。実数等との時と全く同じ感覚でこれらをaの「べき」とか「べき乗」と言います。
この時、次の部分集合H={an|a∊G, nは整数}を考えます。
何かてきとうなGの元に対して、そのべき乗を集めるという事です。
例えばGが0以外の実数・演算は乗法であるとして、てきとうに「3」を選んでH={1,3,32,33,34,・・・,3-1,3-2,3-3,3-4,・・・}を考えるという事です。【30=1, 31=3】
この時、Gが群であれば、H={an|a∊G, nは整数}は必ず部分群になります。これは、定義から示してもよいですが前述の「部分群であるための必要十分条件」を考えるとより簡単であり、an∊Hかつam∊Hのもとでana-m=an-m∊Hとなるので確かに部分であるという事になります。anam=aman(=an+m)なので、これは可換群です。このような部分群Hを、特に「巡回部分群」と呼び、H=<a>と書く事があります。この場合にaを「Hの生成元」と言う事もあります。
Gが群の時、H={an|a∊G, nは整数}を「巡回部分群」と呼びます。
- H=<a>とも書く
- aを「生成元」とも言う
- 可換群である
加群の場合には、特に<a>={na|a∊G, nは整数}と書けます。
【★ 似た用語として、置換の1つの種類として「巡回置換」がありますが区別する必要があります。】
G自体が{an|a∊G, nは整数}として表される時にはGを「巡回群」と呼びます。
正規部分群
群Gに対して部分群Sがあったとき、t∊G【Sに含まれていてもそうでなくてもよい】とs∊Sを組み合わせたt-1stという積を考えます。これを元とする集合も部分群になり「Sに共役な部分群」と言います。
Gが群、SがGの部分群でt∊G, s∊Sのとき、次の集合を「Sに共役な部分群」と言います。
t-1St={t-1st |t∊G, s∊S }
これが本当に部分群になるかは、再び
「『群Gの部分集合HがGの部分群である』⇔『a∊Hかつb∊H ⇒ ab-1∊H』」
の、部分群であるための必要十分条件の関係から見るとすぐに示せます。
s∊Sかつu∊Sのもとで、
(t-1st)(t-1ut)-1=(t-1st)(t-1u-1t)=t-1stt-1u-1t=t-1(su-1)t∊S
よって、集合{t-1st |t∊G, s∊S }はGの部分群です。
【Sは部分群なので、u∊H ⇒ u―1∊H(上記で証明済です)なのでsu―1∊Sです。
また、群の元に関する公式 (ab)-1=b-1a-1の関係に注意。】
さて、群Gに対して部分群Nがあれば「Nに共役な部分群」も必ずある事になりますが、この「Nに共役な部分群」がN自身であり、しかもN自身以外にはありえない時はNをGの「正規部分群」と呼びます。
「『Nに共役な部分群』(必ず存在)がN自身しかない」 時、NをGの「正規部分群」と呼びます。
式で書くと、任意のt∊Gに対し{t-1nt|n∊N}=N,
もしくはt-1Nt=N
もしくはtN=Ntなどと表されます。
tがGの要素でNの要素でない時、n∊Nに対してt-1n\(\notin\)Nかつnt\(\notin\)Nです。
しかしそれらとtやt-1の積の(t-1n)t=t-1(nt)=t-1ntはNの元になり得ます。
Nが群Gの正規部分群である時は、t-1ntがNの元であり、かつnをNの中全体に渡って動かした時にNの中の全ての元になっている事を意味します。
少し理屈が込み入るようですが、この「正規部分群」とは具体例を探すと割と多くあるもので、
例えば「可換群の部分群」は全て正規部分群です。
【∵任意のn∊Nに対してt-1nt=nt-1t=nより、t-1Nt=N】
群Gに対するG自身や単位元だけの群{e}も正規部分群に該当し、「自明な正規部分群」と言います。
Gの正規部分群がこの「自明な正規部分群」しか存在しない時、Gを「単純群」と呼ぶ事があります。
「では非可換な群の部分群で、うまい具合にt-1Nt=Nなどという関係になるものがあるのか?」
結論を言うと、あります。非可換な群で重要なものとして置換全体から成る群がありますが、n次(n個の番号が対象)の置換全体に対して「n次の偶置換(操作回数が偶数回)全体の群」は正規部分群です。
また、4次の置換全体に対してはそれとは別の1つの正規部分群が存在します。
その他に、群Gの元a、bに対してa-1b-1abを考え、これを元とする「交換子群」も正規部分群になります(Gが可換か非可換かに関わらず)。
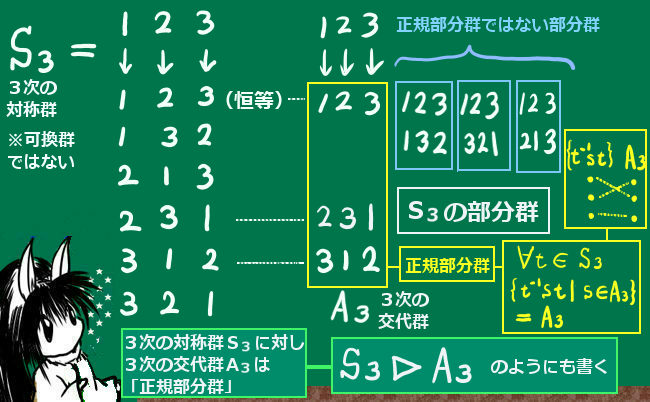
この正規部分群というのは群論の基礎理論のなかで重要な役割を持っています。