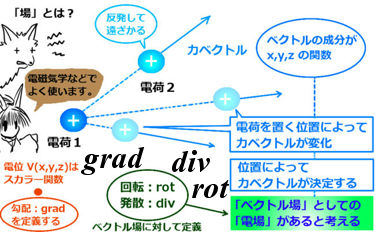
このページでは、電磁気学などで使われる「ベクトル解析」という数学の分野について説明します。
その中でも特に、勾配・発散・回転と呼ばれるものについての説明を行います。
これは「ベクトルの微積分・力学での応用」の延長線上にある理論です。純粋数学よりも、応用数学の色彩の濃い微積分学の分野になります。(もちろん、純粋数学的・解析学的に考察する事も可能です。)
◆関連項目(サイト内リンク):
- 法線面積分の定義
- 接線線積分の定義と考え方
- ガウスの発散定理【証明】
- ガウスの法則【電磁気学】
- ベクトルの考え方:スカラーとの違い(初歩的な内容)
- 偏微分の定義と公式
- 位置エネルギーと保存力の関係(勾配ベクトル の応用例。偏微分の応用でもあります。)

はじめに:「場」という考え方とベクトル解析
勾配(grad)、発散(div)、回転(rot)は「スカラー場」や「ベクトル場」というものに対して考えます。それらはいずれもスカラーやベクトルの仲間なのですが、特にどのようなスカラーやベクトルをそのように呼ぶのかを最初に述べておきます。
■ ベクトル場
■ スカラー場
■ 電磁気学でのベクトル場とスカラー場の例
ベクトル場
てきとうな電荷があって、まわりに別の電荷を持ってくると、電荷同士に力が働きます。この時に、後から持ってきたほうの電荷を置く場所によって働く力が変わってきます。これは数式で表すと、電荷が受ける力が座標上の点ごとに異なると考える事もできて、力を座標変数の関数で表されたベクトルで表せます。このように表されるベクトルを、「ベクトル場」と呼びます。ベクトル場の各成分は、座標成分による多変数関数になっています。(必要に応じて時間変化もするとして時間成分も加えます。)
このようなベクトル場の微積分を扱う数学の分野をベクトル解析と呼んだりします。後述するスカラー場の微積分も合わせて考えます(スカラーをベクトルに変換する操作などが含まれます) 。
★ ベクトル場の事を「ベクトル界」と言う事もあります。ベクトル界という呼び方は工学系で使われる事が多いとも言われます。
どちらが正しいかの基準はありませんが、このサイトでは、「ベクトル場」の呼び方を使用します。
「場(field)」という語は、「遠隔力」という考え方に対する概念として物理学で単独でも使う事があります。他方、『界』という語は単独では普通は使わない事が多いので、用語としては「場」という語でこのサイトでは統一します。
x, y, z の直交座標上で、
次のように各成分が x, y, z の関数として表される空間ベクトルを「ベクトル場」と呼びます:
$$\overrightarrow {F}(x,y,z)=(\hspace{3pt}F_1(x,y,z),F_2(x,y,z),F_3(x,y,z)\hspace{3pt})$$
$$ベクトルの各成分\hspace{3pt}F_1(x,y,z)などは、x,y,z の多変数関数(スカラー関数)$$
平面ベクトルで考えたとしても、成分が1つ減るだけで同様にベクトル場を考える事ができます。4成分以上の場合も理論的には考える事は可能ですが、普通はあまり考えません。ここでは基本的に3成分の空間ベクトルのベクトル場を考えます。
ベクトル場自体は多変数関数を成分とする「ベクトル」とも言えるので、上記の形が「ベクトル場の『定義』」であるというよりは、ベクトルのうち「このような形で表されるものを特にベクトル場と呼ぶ」という感じだと言えます。
物体の軌道をベクトルで表す時に、物体の位置座標を「時間の関数」として表す方法があったわけですが、それとの違いは、成分となる関数の変数に「座標成分が含まれている」という事です。
$$\overrightarrow {X}(t)=(x(t),y(t),z(t)) といったベクトルとは少し区別されるのです。$$
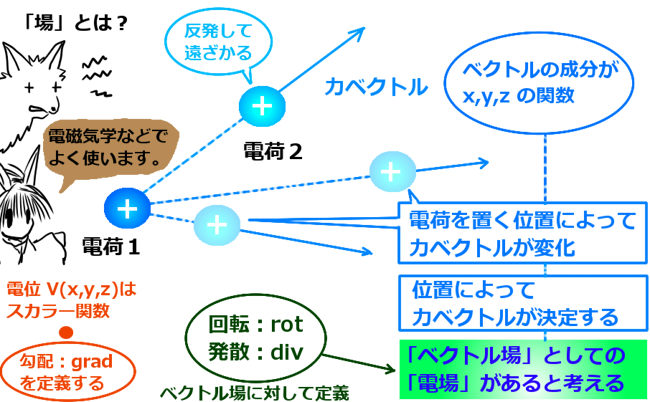
向きは2つの電荷を結ぶ直線に沿い、遠くに離れるほど力の大きさは弱くなります。
「電荷に働く力を「場」として見る場合は「電場」と呼びます。
スカラー場
もう1つ、ベクトル解析では「スカラー場」というものも考えて、ベクトル場との使い分けを上手に行う事が理解のポイントになっていきます。
スカラー場とは、数式的には座標成分 x, y, z を変数とする多変数関数の事です。意味としては何ら難しくないのですが、電磁気学等の理論ではベクトル場と入り乱れる形で使われるので、物理の理論の中では慣れないと少し難しく感じると思います。
x, y, z の直交座標上で、
次のように x, y, z の関数として表される多変数関数を「スカラー場」と呼びます:
$$\phi= \phi (x,y,z)$$
記号はここでは「\(\phi\)ファイ」を用いていますが、別に何でも構いません。
これは数学的に見れば通常の多変数関数であって、これをスカラー場と呼ぶのは基本的には x, y, z が空間上の直交座標の成分である事が明確であって物理等で用いられる場合、特にベクトル場と区別する場合です。
電磁気学でのベクトル場とスカラー場の例
+1[C] の電荷をある場所に置いたときに、その電荷が受ける力ベクトルを位置座標の関数で表したものはベクトル場であり、特に電場と呼びます。電気だけでなく磁気についても同じ考え方ができます。磁気の場合は単独の「磁荷」は存在しないと言われていますが、仮想的に単独の「磁荷」を考えて、磁荷が受ける力のベクトル場の事を磁場と呼びます。
電磁気学では、これを総称して電磁場と呼んだりもします。磁場は電流によって作られ、電流を生じさせる電圧(起電力)は磁場の変化によって作られるという関係が知られています。電磁気学は、観測によって得られたそれらの関係を定量的に表せるように数式で整理する物理学の分野です。
ベクトル場の具体例として、+1[C] の電荷のまわりの電場は次のように表せます(その付近に、別の+1[C] の電荷を持ってくると考えます。k は比例定数です。 ):
$$\overrightarrow {E}(x,y,z)=\left(\frac{kx}{r^3}, \frac{ky}{r^3}, \frac{kz}{r^3} \right)= \left (\frac{kx}{(x^2+y^2+z^2)^{\frac{3}{2}}}, \frac{ky}{(x^2+y^2+z^2)^{\frac{3}{2}}}, \frac{kz}{(x^2+y^2+z^2)^{\frac{3}{2}}} \right )$$
$$r= \sqrt{x^2+y^2+z^2} = (x^2+y^2+z^2)^{\frac{1}{2}}の関係で処理しています。 \frac{kx}{r^3} =\frac{k}{r^2}\cdot \frac{x}{r}という事です。 $$
$$詳細は別途に記しますが、ここでの電場の「大きさ」は| \overrightarrow {E} |=\frac{k}{r^2}になります。$$
ただし、このように具体的な座標成分で記すと計算が面倒なので、大枠となる理論ではベクトル場という事だけ踏まえて数式的な処理を加えていく事が行われます。個々の具体的な事例の考察では具体的な関数にして考えたりします。
このようなベクトル場である電場に対して、ある位置での+1[C]の電荷が持つ事になる位置エネルギー(または「ポテンシャル」)を電位と言います。これは日常でもよく耳にすると思われる電圧と本質的には同じものです。電位は、ベクトルでは無く、スカラー場になります。つまり、x, y, z という3つの変数によって決まる1つの値が決まるという3変数関数になります。
$$「電位」V(x,y,z) はべクトル場ではなく、スカラー場です。$$
これらのベクトル場やスカラー場の微積分を考えられる時に使われるのが、次に記す「勾配」「発散」「回転」というものです。
ベクトル場の発散(div)と回転(rot)、スカラー場の勾配(grad)
ではここで、ベクトル解析で重要な 勾配、発散、回転 と呼ばれるものの説明をします。
■ div, rot, grad ・・定義と考え方
■ 図形的にはどのような意味を持つ?
※ここでの「発散」は、「無限大に発散」という意味ではなく、また別のものです。少々分かりにくいかもしれませんが、同じ用語を使う習慣があります。
※「回転」は「循環」と呼ばれる場合もあります。
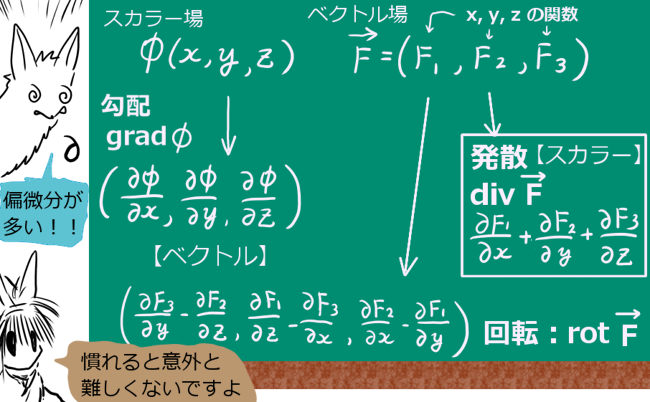
ベクトル場、スカラー場ともに多変数関数である事が直接的に関わっています。
div, rot, grad ・・定義と考え方
あるベクトル場 \(\overrightarrow {F}\) があったとき、それに対する発散、回転を考える事になります。(成分が x, y, z の関数になっていない通常の「ベクトル」に対しては基本的に考えないので注意。)
他方、勾配についてはスカラー場に対して定義します。
$$ベクトル場\overrightarrow {F}(x,y,z)に対して、発散:\mathrm{div} \overrightarrow {F},\hspace{10pt} 回転:\mathrm{rot} \overrightarrow {F},\hspace{10pt} を定義します。$$
$$また、スカラー場\phi (x,y,z)に対して、 勾配:\mathrm{grad} \phi ,\hspace{10pt} を定義します。$$
勾配(gradient)【グレディエント】
- スカラー場 \(\phi (x,y,z)\)に対して次のベクトル(関数)を勾配(勾配ベクトル)と呼びます。
$$\mathrm{grad} \phi=\left(\frac{\partial \phi}{\partial x},\frac{\partial \phi}{\partial y},\frac{\partial \phi}{\partial z}\right)$$
- \(\mathrm{grad}\phiの代わりに\nabla \phi とも書きます。\)
発散(divergence)【ダイヴァージェンス】
-
ベクトル場 \(\overrightarrow {F}(x,y,z)=(F_1,F_2,F_3)\) に対する次のスカラー(関数)を発散と呼びます。
$$\mathrm{div} \overrightarrow {F}=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}$$ -
\(\mathrm{div}\overrightarrow {A}の代わりに\nabla \cdot \overrightarrow {A} とも書きます。\)
\((F_1,F_2,F_3)=(F_1(x,y,z),F_2(x,y,z),F_3(x,y,z))\) です。
回転(rotation,curl)【ローテイション、カール】
- ベクトル場 \(\overrightarrow {F}(x,y,z)=(F_1,F_2,F_3)\) に対する次のベクトル(関数)を回転と呼びます。$$\mathrm{rot} \overrightarrow {A}=\left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z}, \frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x}, \frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right)$$
- \(\mathrm{rot}\overrightarrow {A}の代わりに\mathrm{curl}\overrightarrow {A}、あるいは\nabla × \overrightarrow {A} とも書きます。\)
★ 見ての通り、いずれも偏微分を用いて定義されます。
偏微分とは、1つの変数だけに着目し、他の変数は定数扱いにして微分操作を行う演算です。
★ \(\nabla \cdot \overrightarrow {A},\nabla × \overrightarrow {A}\) という表記について:これらの定義による式の形が、ベクトルの内積や外積の計算規則と似ている事からそのようにも書く習慣があります。この逆三角形の記号∇は「ナブラ」と呼ばれます。
★ 勾配・発散・回転自体も x, y, z を変数とするベクトルや実関数ですからベクトル場とスカラー場という事になりますが、勾配・発散・回転自体に対してはあまり「場」とは言わない事が多いです。
このように定義した時、
勾配と回転はベクトルであり、発散はスカラーである事に、少し注意してみてください。
同時に、勾配を考える対象はスカラー場であり、
発散と回転を考える対象はベクトル場であるわけです。少し整理しましょう。
| 対象の関数 | 勾配・発散・回転 | ベクトル・スカラーの区別 |
|---|---|---|
| スカラー場\(\phi (x,y,z)\) | \(\mathrm{grad}\phi \) | 勾配:ベクトル(成分は関数) |
| ベクトル場 \(\overrightarrow {F}(x,y,z)\) | \(\mathrm{div}\overrightarrow {F}\) | 発散:スカラー(関数) |
| ベクトル場 \(\overrightarrow {F}(x,y,z)\) | \(\mathrm{rot}\overrightarrow {F}\) | 回転:ベクトル(成分は関数) |
★ 尚、発散と回転については、上記で定義した数式を「積分した形」を発散および回転と呼ぶ場合もありますが、このサイトでは一貫して上記の形の定義を用いる事にします。
図形的にはどのような意味を持つ?
こういった色々見慣れない記号をなぜ考えるのか?という話にもなるかと思いますが、これらに関しては基本的に「3次元の空間」の中のベクトルの理論ですので、図形的を持っている事が理解の1つのポイントです。
まず勾配については、偏微分を考えている事に注目すると、あるスカラー場が x方向、y方向、z方向に対して、その向きだけの変化率をベクトルで表したものになります。
次に、ベクトル場の発散についてです。これは位置が微小変化した時に、特定の量が全体として「周りからどれだけ出入りするか」の変化率を表します。単位体積から出入りする流量(※1)を表すとも言えます。
ベクトル場の発散に体積要素(dv = dxdydz)を掛け算すると、微小な領域に出入りする流量を表します。発散を面積分と重積分(※2) を結びつける公式(発散定理、ガウスの定理)もあり、それも物理で重要です。
(※1)もう少し詳しく言いますと、電磁気学の理論の一部は、流体力学の理論とのアナロジー(類似性)から類推して組み立てられています。「流量」とは流体力学で使われる用語であり、ある断面を1秒間あたりに通過する流体の体積を表します。
(※2)この場合、dv = dxdydz を考えるので体積積分とも言います)
回転については、定義式からは少し分かり辛いと思いますが、じつはこれを積分(「法線面積分」という種類の積分)をした時に文字通りの意味を表します。公式(「ストークスの定理」)を用いる事で、あるベクトル場の回転の面積分は、そのベクトル場に対して閉曲線を1周するように接線線積分したものに等しくなるのです。ベクトル場の回転は流体力学では「渦」を表現するのに使い、電磁気学などの領域でも使用します。
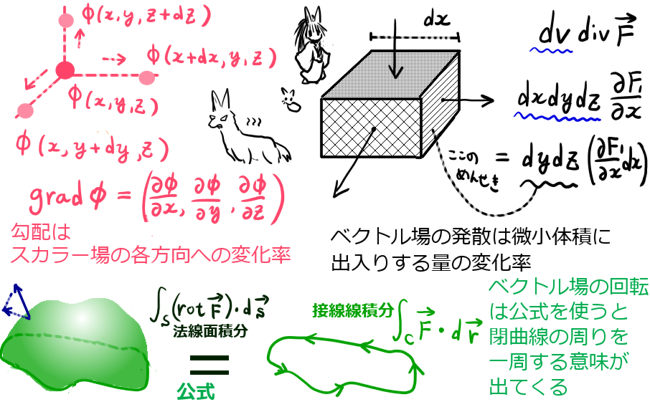
勾配・発散・回転に関するいくつかの公式
最後に、いくつかの公式について紹介をしておきましょう。
■ 勾配・発散・回転の公式①:色々な組み合わせによる関係式
■ 勾配・発散・回転の公式②:積分を含む公式
勾配・発散・回転の公式①:色々な組み合わせによる関係式
ベクトル場の勾配・発散・回転を使ってどういう理論が展開されるのかを軽く見るために、いくつかの公式を挙げてみます。これらは、一般的には暗記するほど重要ではないと思いますが、簡単なものや特徴的なものは知っておくと物理学全般を学ぶ時に便利です。
\(\phi\) などはスカラー場、\(\overrightarrow {F}\) などはベクトル場であるとします。
- \(\mathrm{grad}(\phi_1\phi_2)=\phi_1(\mathrm{grad}\phi_2)+\phi_2(\mathrm{grad}\phi_1)\)
- \(\mathrm{div}(\phi\overrightarrow {F})=\mathrm{div}(\overrightarrow {F}\cdot \mathrm{grad}\phi)+\phi\mathrm{div}\overrightarrow {F}\)
- \(\mathrm{rot}(\mathrm{grad}\phi)=0\)
- \(\mathrm{div}(\mathrm{rot}\overrightarrow {F})=0\)
- \(\mathrm{rot}(\mathrm{rot}\overrightarrow {F})=\mathrm{grad}(\mathrm{div}\overrightarrow {F})-\left(\frac{\partial ^2F_1}{\partial x^2}+\frac{\partial^2 F_2}{\partial y^2}+\frac{\partial^2 F_3}{\partial z^2}\right)\)
\(\phi_1\phi_2\) は2つのスカラー場の積(普通の掛け算)であり、\(\phi\overrightarrow {F}\) はベクトル場の各成分に(同一の)スカラー場を掛け算したものです。\(\overrightarrow {F}\cdot \mathrm{grad}\phi\) は、内積です。
電磁気学の理論では、3番目と4番目の関係は特に重要です。
5番目の形の式は、回転はベクトル場から別のベクトル(場)を作る操作であるために考える事ができる点に注意。(勾配や発散では同じような事はできません。)
これらの公式の証明は、基本的には定義に直接当てはめて、積の微分公式などの基本公式を使って丁寧に計算する事で得られます。例えば、1番目の公式は各成分ごとに積の微分公式を使うだけです。
(偏微分の場合も通常の微分の場合と同じ形の積の微分公式が成立します。)
$$\mathrm{grad}(\phi_1\phi_2)=\left(\frac{\partial (\phi_1\phi_2) }{\partial x},\frac{\partial (\phi_1\phi_2) }{\partial y},\frac{\partial \ (\phi_1\phi_2) }{\partial z}\right)$$
$$= \left( \phi_1 \frac{\partial \phi_2}{\partial x}+ \phi_2 \frac{\partial \phi_1}{\partial x} , \phi_1 \frac{\partial \phi_2}{\partial y}+ \phi_2 \frac{\partial \phi_1 }{\partial y} , \phi_1 \frac{\partial \phi_2 }{\partial z}+ \phi_2 \frac{\partial \phi_1 }{\partial z} \right) $$
$$= \left( \phi_1 \frac{\partial \phi_2}{\partial x} , \phi_1 \frac{\partial \phi_2}{\partial y} , \phi_1 \frac{\partial \phi_2 }{\partial z}\right) + \left(\phi_2 \frac{\partial \phi_1}{\partial x} , \phi_2 \frac{\partial \phi_1 }{\partial y}, \phi_2 \frac{\partial \phi_1 }{\partial z} \right) $$
$$=\phi_1(\mathrm{grad}\phi_2)+\phi_2(\mathrm{grad}\phi_1)【1番目の公式の証明終り】$$
2番目の公式も、積の微分公式を用いるだけです。
$$\mathrm{div}(\phi\overrightarrow {F})=\frac{\partial (\phi F_1)}{\partial x}+\frac{\partial (\phi F_2)}{\partial y}+\frac{\partial (\phi F_3)}{\partial z} $$
$$ = \left( \phi \frac{\partial F_1}{\partial x}+ F_1 \frac{\partial \phi }{\partial x} \right) + \left( \phi \frac{\partial F_2}{\partial y}+ F_2 \frac{\partial \phi }{\partial y} \right) + \left( \phi \frac{\partial F_3}{\partial z} +F_3 \frac{\partial \phi }{\partial z} \right) $$
$$ = \phi \left( \frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+ \frac{\partial F_3}{\partial z}\right) + F_1 \frac{\partial \phi }{\partial x} + F_2 \frac{\partial \phi }{\partial y} + F_3 \frac{\partial \phi }{\partial z} $$
$$= \phi \mathrm{div} \overrightarrow {F}+ \overrightarrow {F} \cdot \mathrm{grad}\phi 【2番目の公式の証明終り】 $$
3番目と4番目の式は、2つの変数で続けて偏微分を行う時には偏微分の順番は関係なく同じ結果になる(※)という事を使って示します。【※解析学的に厳密に言うと条件がありますが、通常の連続関数であれば基本的に問題ありません。】
3成分のそれぞれについて0になる事を示す必要がありますが、変数が入れ替わるだけで同じ形・同じ計算ですので、第1成分(x成分)についてのみ記します。
$$\mathrm{rot}(\mathrm{grad}\phi)の第1成分=\frac{\partial}{\partial y} \left(\frac{\partial \phi}{\partial z}\right)- \frac{\partial}{\partial z} \left (\frac{\partial \phi}{\partial y} \right) = \frac{\partial^2 \phi}{\partial z \partial y }- \frac{\partial^2 \phi}{\partial y \partial z }=0 $$
$$【3番目の公式(第1成分)証明終り】 $$
$$\mathrm{div}(\mathrm{rot}\overrightarrow {F})の第1成分= \mathrm{div} \left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z},
\frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x},
\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right)$$
$$= \frac{\partial}{\partial x} \left(\frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z} \right) + \frac{\partial}{\partial y} \left( \frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x} \right) + \frac{\partial}{\partial z} \left( \frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y}\right) $$
$$= \left( \frac{\partial^2 F_3 }{\partial x \partial y }- \frac{\partial^2 F_3 }{\partial y \partial x } \right) + \left( \frac{\partial^2 F_1 }{\partial y \partial z }- \frac{\partial^2 F_1 }{\partial z \partial y } \right) + \left( \frac{\partial^2 F_2 }{\partial z \partial x }- \frac{\partial^2 F_2 }{\partial x \partial z } \right) =0 $$
$$【4番目の公式(第1成分)証明終り】(最後の式では消える項ごとにまとめました。) $$
5番目の公式に関しては少々計算が面倒ですが、定義に当てはめて丁寧に計算する事で結果が得られます。特別な定理や計算技巧は必要ありません。
この他にも、勾配・発散・回転の組み合わせによる色々な公式が存在します。
勾配・発散・回転の公式②:積分を含む公式
勾配・発散・回転のいずれも微分(偏微分)を使って定義されるものであるわけですが、発散と回転に関してはそれらに対する積分を考える事で独特な形の公式が成立します。しかも、それらは物理の理論の中でも重要です。
2つの公式を、ごく簡単にですが挙げておきます。上記でも少し触れた「発散定理(ガウスの定理)」と「ストークスの定理」です。これらは積分を含む公式であり、通常の積分ではなく「法線面積分」「接線線積分」「体積積分」という種類の積分が含まれます。
$$発散定理:\int_V \mathrm{div}\overrightarrow{F} dv = \int_S \overrightarrow{F}\cdot d\overrightarrow{s}$$ $$ストークスの定理:\int_S \mathrm{rot}\overrightarrow{A}\cdot d\overrightarrow{s} = \int_C \overrightarrow{A}\cdot d\overrightarrow{r}$$ここでは、C:閉曲線、S:閉曲面の表面、V:閉曲面内の領域 を表しています。
接線線積分については力学でも使う考え方ですが、法線面積分については初歩的な運動の解析にはあまり使わないかもしれません。基本的な考え方は共通していて、微小な領域において内積の計算をしてから積分をする(合計する)というものです。
体積積分は重積分で表す事もでき、法線面積分も内積の処理をした後に重積分として表す事もできます。(しかも、その事が証明で重要です。)
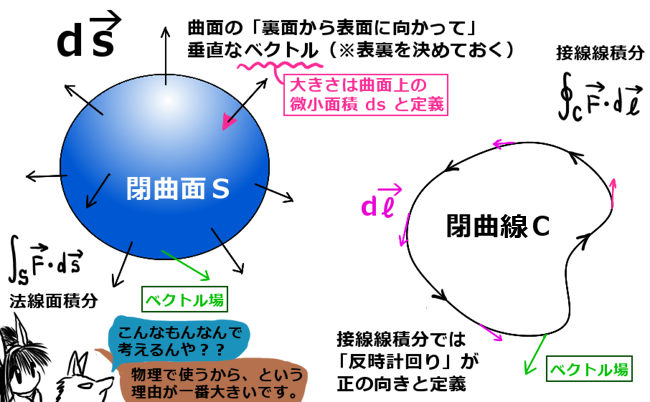
空間上に閉曲線がある場合には、閉曲線を外周とする曲面の表側を決めたうえで、接線線積分の積分方向を定めます。
このベクトル解析の領域は、物理の電磁気学や流体力学と合わせて学んでみる事がおすすめです。数学的に詳しい考察が必要な部分と、応用で重要になる部分との関連がよく分かるようになると思います。