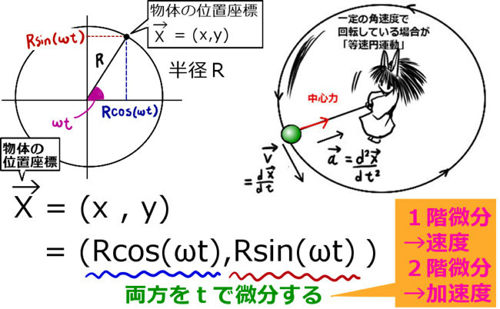
ベクトルに対する微分と積分について、古典力学での使われ方を例に具体的に見て行きます。
■ベクトルの基本事項(高校数学)や、逆にこのページの内容の発展事項であるベクトル解析については別途に述べています。
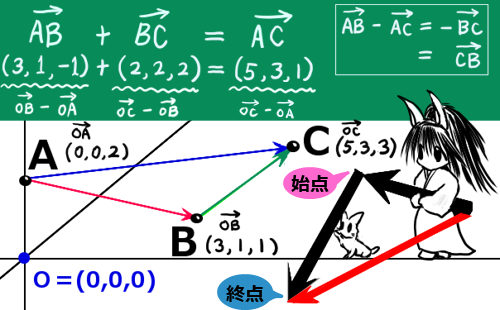
物理で重要な事は、2つの方向への力同士の「合力」は、ベクトルの加算・減算によって計算すればうまく行く事が「実験で」確かめられているという事です。運動方程式により加速度は力に比例しますから、加速度の加算・減算もベクトルで行う事ができます。(また、速度に関しても同じようにベクトルで考えてよい事になります。)
ベクトルの微分と積分の定義
では、ベクトルの微分の定義を説明いたします。定義自体は、簡単です。
それぞれの成分を微分したものを考えるという、それだけです。
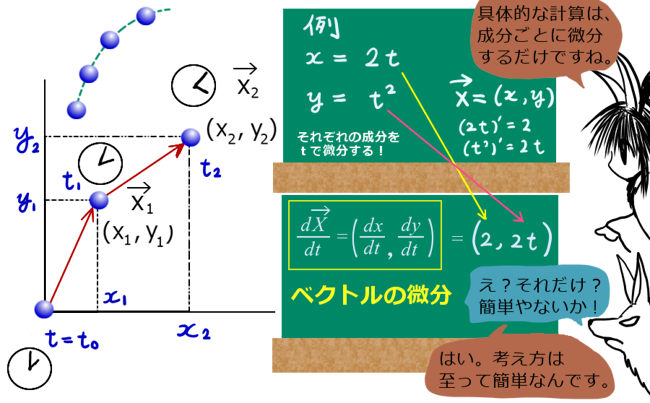
位置座標を表すベクトルの各成分をある1つの変数で微分したものを、ベクトルの微分と呼び、ベクトルに対して微分操作の記号をつけた \(\frac{d}{dt}\overrightarrow{X}(t)\) という表記を行います。 \(\frac{d \overrightarrow{X}(t) }{dt}\) などと書いても同じです。
3次元の空間ベクトルの場合を記しますが、何次元ベクトルでも同じです。 $$\frac{d}{dt}\overrightarrow{X}(t)=\left(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\right)$$ $$x,y,z はtの関数:x=x(t), y=y(t), z=z(t)$$ この共通の変数の事を、数学的には「パラメータ」または「媒介変数」と言います。
ベクトルの微分などと言うと一見わけがわからないように思えるかもしれませんが、このように意味と定義を丁寧に見ると、それほど難しくはないのではないでしょうか?表記については確かに慣れないと扱いにくさを感じるかもしれませんが、少しずつ触れていけば慣れると思います。
ただし、何で微分するかには少しだけ注意すべきで、力学などで物体の「位置」と時間の関係を分析する場合は、時間tで微分します。この時、各成分は時間の関数で表すものとします。(そうでなければ、当然tでの微分はできません。)
ベクトルの微積分を1つの変数tで行う時は、
ベクトル(x, y, z)の各成分 x, y, z が「tの関数」x(t), y(t), z(t) である場合を考えます。
例えば、\(x(t)=2t, y(t)=3t, z(t)=t^2\) などです。
この成分を持つベクトルをtで微分するのであれば、
それぞれの成分をtで微分すればそれでよいというわけです。
例えば、運動する物体の位置座標を(x, y , z)とした時、この座標が時間ごとに変化するので x, y, z は「時間tの関数で表せるはず」と考えるわけです。しかも、物体は連続的に動くはずなので、その時間変数 t で「微分も可能である」と考えるわけです。物体の位置座標を表すベクトルの時間微分を、物理では特に速度ベクトルと呼びます。
ベクトルの高階微分についても考え方は同じで、各成分を2階微分したものを、そのベクトルの2階微分として表記します。位置座標を表すベクトルの時間変数tによる2階微分は、加速度ベクトルと呼ばれます。
微分が可能であるという事は、積分も可能です。
ベクトルに対する積分も基本的に同じ考えであり、ベクトルの各成分を同じ変数で積分したものを、1つのベクトルに対する積分として表示します。
不定積分で記しますが、定積分でも同じです。 $$\int \overrightarrow{X}(t)dt=\left(\int x(t)dt,\int y(t)dt,\int z(t)dt \right)$$ また、微分されたベクトルを積分すれば、「各成分の微分」の積分ですから、もとのベクトルに戻ります。つまり表記上、ベクトルに関しても「微積分学の基本定理」が成立します。 $$\int \frac{d}{dt}\overrightarrow{X}(t)dt=\left(\int \frac{d}{dt}x(t)dt,\int \frac{d}{dt}y(t)dt,\int \frac{d}{dt}z(t)dt \right) $$ $$=\left(x(t)+C_1,y(t)+C_2,z(t)+C_3 \right)= \left(x(t),y(t),z(t) \right)+(C_1,C_2,C_3)=\overrightarrow{X}(t)+\overrightarrow{C}$$ $$\overrightarrow{C}は定ベクトルで、\overrightarrow{C}=(C_1,C_2,C_3)$$
ベクトルの積分に関しては、後述しますように、「内積の計算をしてから積分する」というものもあります。これは接線線積分や面積分の考え方であり、物理への応用で重要な考え方になります。
応用例:ベクトルの微分による等速円運動の考察
力学の基本的な例の1つとして、等速円運動というものがあります。これは、その名の通り、同じ「速さ」で円運動を延々とぐるぐるしている運動を言います。
ここで「等速円運動」とは「速さ」が同じである運動を指していて、「速度」は各位置ごとに異なります。なぜかというと、円運動なので向きが常に変化しているためです。
ベクトルで言うと速度ベクトルの「大きさ」だけが一定で、向きは各位置ごとに常に変化するという運動である事を指します。
そのように物体が等速円運動をしている時、「いったいどのような力が物体に働けば、そのような運動が生じるだろう?」という問題があります。
これは、結論を先に言うと「円の中心に向かって同じ大きさの力が働けばよい」というのが答えです。これを数学的にどのように導出するのか?と言うと、まず運動方程式を考える必要があります。それと、べクトルを考える事がポイントです。以下、具体的に見ていきましょう。
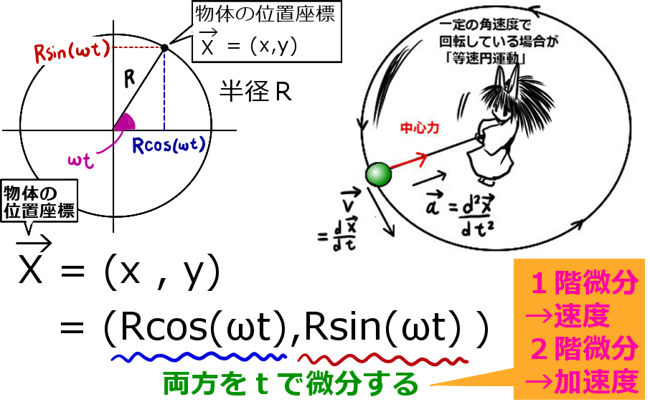
少し数学的に込み入る話ですが、
座標成分自体を極座標に変換して運動方程式を考える事もできます。
すなわち、速度ベクトル、加速度ベクトル、力ベクトルの成分を「x成分」と「y成分」ではなく「r成分」と「θ成分」で表す方法です。
ただしここではその考え方をする必要は無く、ベクトル自体の成分は直交座標系のx,y,zの成分で考えれば良い事になります。
空間上の運動に対して運動方程式を作る時は、ベクトルのそれぞれの成分に対して運動方程式を作ります。つまり、1つの運動に対して運動方程式は「3つ」できるのです。その3式を解く事で、運動の分析ができるというのが、初歩的な力学での一般論です。
$$\overrightarrow{F}=m\frac{d^2 \overrightarrow{X}}{dt^2}$$ $$\overrightarrow{F}=(F_x,F_y,F_z),\hspace{5pt}\overrightarrow{X}=(x(t),y(t),z(t))$$ つまり(最大で)3つの微分方程式ができます。 $$①F_x=m\frac{d^2x}{dt^2},\hspace{10pt}②F_y=m\frac{d^2y}{dt^2},\hspace{10pt}③F_z=m\frac{d^2z}{dt^2}$$ (初歩的な微分方程式の解き方については以前の記事で詳しく記しています。)
ただし、この等速円運動の分析の場合では、じつは式は「2つ」でよいのです。その理由は次の通りです。
同じ円運動といっても、空間上であらゆる角度に傾いた平面上の円運動が考えられます。しかし、物理ではこのような時、「座標系のほうを物体の運動に合わせてあげる」ということをやります。実際に物体が運動している平面に、xy平面を合わせてあげるのです。
すると、z軸方向には物体は運動しておらず、どんな時刻でも位置座標のz成分は0ですから、あってもなくても同じ事であって、考察の対象から除外します。こういう事は、物理でよくやります。
ですので、運動方程式をベクトルの各成分に対して作る時も、
z成分については\(F_z=m\cdot 0=0[N]\) 「力は一切働いてません」という、数式で考察するまでもない結果が出るだけなので、「考えなくてよい」とするわけです。
というわけで、平面ベクトルで表される運動として、分析をします。
この時、極座標を使うと話は単純になり、計算も楽です。等速でぐるぐる回っているという条件から、一定の角速度\(\omega\)[rad/s]【rad:ラジアン(これは省略する事もできます)s:秒】で運動していると捉えます。
すると、物体の位置座標はどのように表せるかというと、三角関数を用いればよいのです。円の半径をR[m] 【m:メートル】とすると、x座標は R cos(ω t)、y座標はR sin (ω t) になります。
ベクトルで書くなら、\(\overrightarrow{X}=(R \cos (\omega t),R \sin (\omega t))\)
この場合は、位置座標の成分が時間の関数として明確になっているので、これを時間tで2階微分して加速度にして、質量mを掛け算すれば「力」になります。ですから、ここでは微分方程式を解く必要はありません。
x = R cos(ω t) と y = R sin (ω t) を、tで2階微分しましょう。これは、合成関数の微分になっているので1回の微分ごとに ω が掛け算される事に注意する以外は、初歩的な微分計算ですので結果はすぐに出ます。結論は次の通りです。
$$\frac{d^2x}{dt^2}=-R\omega^2 \cos (ω t) ,\hspace{10pt} \frac{d^2y}{dt^2}=-R\omega^2 \sin (ω t) $$
$$ \overrightarrow{F} =m\frac{d^2 \overrightarrow{X}}{dt^2}=( -R\omega^2 \cos (ω t) , -R\omega^2 \sin (ω t) )=-mR\omega^2( \cos(ω t), \sin(ω t) )= -mR\omega^2 \overrightarrow{X} $$
この結果から、考察できる事はいくつかあります。
- 力の「向き」は常に中心方向を向いている:
結果を見ると、元の位置座標の定数倍で、しかもマイナスがついています。これは、物体から見ると、力のベクトルが原点を向いている事を意味するのです。
(★位置座標のベクトルは原点から物体に向かう向きのベクトルである事に注意。) - 力の大きさは、時間によらず定数:
力の大きさは、「力ベクトルの『大きさ』」を計算すればよいのです。
この時、\(\cos^2(ω t)+\sin^2(ω t)=1 \) である事に注意します。時間を含む部分は、1になって「消えてしまう」わけです。
すると、\(|\overrightarrow{F}|=mR\omega^2\) となります。 - 力の大きさの計算から、
力の大きさは質量、半径、「角速度の2乗」のそれぞれに比例する事が分かります。
等速円運動のように、力ベクトルが常に中心方向を向いているとき、
物理ではそのような力を「中心力」と呼びます。
さらなる学習・ベクトル解析に向けて
今回はこれで終わりますが、ベクトルの微積分の話自体は、じつはまだ続きます。
今回主に扱ったのは、ベクトルの3つの成分が共通の変数の関数、時間tで表される場合でした。
これに対して、物理ではさらに、「位置によって力等が変化する」場合を考えます。
力の種類で言うと、重力や電磁力が該当します。
その場合、ベクトルの各成分が位置座標x、y、zの関数であると考えるのです。
このようなベクトルを「ベクトル場」と言い、それについての種々の微積分を考える領域を、「ベクトル解析」と言います。(このページで扱った内容や、ベクトルの初歩の内容も含めてベクトル解析と呼ぶ事もあります。)
このベクトル解析の考え方は、電磁気学や流体力学で使う他に、物理学一般でも使います。
このベクトル解析の領域は、初見だと多分かなり分かりづらいかと思います。しかし基本的には、今回のページで述べたような、ベクトルを成分ごとに分けて丁寧に考える事、内積の定義に従って丁寧な計算を進める事によって理解できるような体系になっています。