微分の定義とイメージを、図形的な意味と数式の両方の観点から説明します。
微分は積分の逆演算でもありますが、ここでは「関数のグラフの接線の傾き」という図形的な意味に特に着目して説明をします。
■サイト内関連記事:各種の微分に関する公式の証明等です。
微分のイメージと接線
接線の傾き
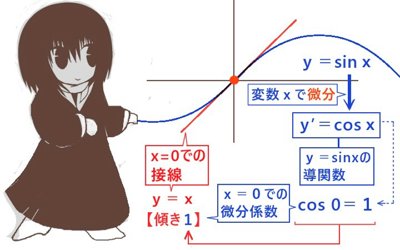
例えばy=sinxを微分すると、その計算結果の公式としてy’=cosxが得られますが、
実はこれは定義域内のy=sinxのグラフ上の任意の点における接線の傾きを表す関数です。
y’=cosxにx=0を代入すると計算結果は1ですがそれは
「x=0におけるy=sinxのグラフの接線の傾き」に一致するのです。
微分のイメージは「曲線の接線の傾き」であり、
実際にその計算による値は関数を表すグラフ上の特定の点での接線の傾きに一致します。
正弦関数以外の三角関数やy=x2やy=x3等の関数、あるいは円を式で表した関数も微分する事が可能で、各点での接線の傾きを計算する事ができます。
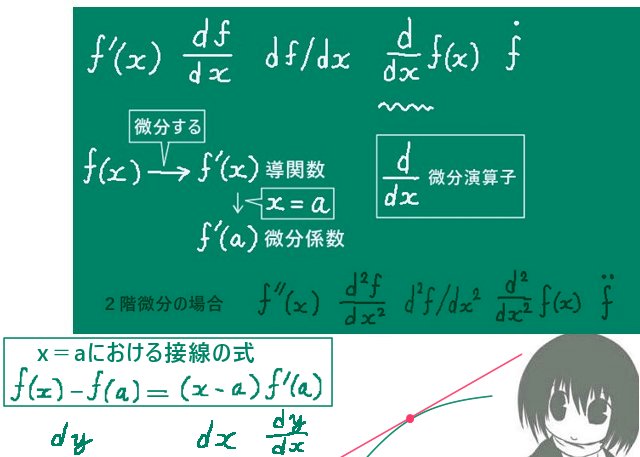
微分を表す記号は、後述するようにy’ f’(x) dy/dxなどです。
ただしそれらは関数として統一的に考えている接線の傾きであり、
x=0での具体的な接線の傾きを知りたい場合にはx=0の値を代入する必要があります。
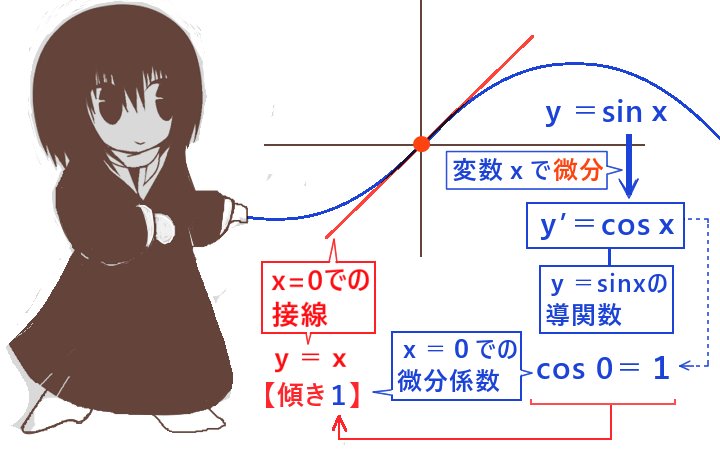
正弦関数y=sinxにおいてx=π/2の部分をグラフ上で見ると、
その部分の接線はx軸に平行で「傾きは0」なのではないかと予想ができます。そして実際にそれは正しくて、微分演算により得るy’=cosxにx=π/2を代入するとy’=0であり、それがx=π/2におけるy=sinxの接線の傾きです。
他方で円を座標上に描いたような時には左右に2箇所、接線がy軸に平行になる部分が存在します。そのような時には接線の傾きは∞(無限大)であるとみなす事もできますが、微分によっては傾きを数値として表せないと考える事が多いです。
微分演算(計算)・導関数・微分係数の関係と使い分け
微分を式で考える場合には、
少しややこしいようですが「微分という演算(計算)」と、
演算の結果として得られる「関数」(各点での接線の傾きを表現)と、
それに変数の値を代入した「数値」(具体的な接線の傾き)があります。
接線の傾きを表す関数は数学的には導関数(「どうかんすう」)と呼ばれ、
導関数に具体的な値を代入して得る値(=具体的な接線の傾き)は微分係数と呼ばれます。
微分係数は「x=0における微分係数」とか「x=1における微分係数」といった形で表現されます。
y=sinxに対して微分演算を行うと
導関数y’=cosxを公式として得る事になり、
導関数y’=cosxにx=0を代入した時の
cos0=1がx=0における微分係数です。
| 関数 | 導関数 | x=0における 微分係数 | x=1における 微分係数 | x=πにおける 微分係数 |
| y=sinx | y’=cosx | 1 | cos1 | -1 |
| y=x2 | y’=2x | 0 | 2 | 2π |
| y=x3 | y’=3x2 | 0 | 3 | 3π2 |
「微分」という語の使われ方
ところで導関数の事を指して単に「微分」と呼ぶ事もあります。
例えば「y=sinxの微分はy’=cosxであるから・・・」などといった具合です。
ただしこれは数学よりもむしろ日本語の用法上の問題であるとも考えられて、
「微分する」事を「・・の微分」と言っているとも見れます。いずれにしても「微分」という言葉の使い方は数学上においてもそれほど厳密ではなく、多少緩く扱ってもよい事になっているのが実情と思われます。実質的には「微分」という語は演算を指す事を基本としながらも、便宜的に「導関数」と同義の語としても使われています。
しかし「導関数は関数」であり「微分係数は定数」であるため、
「導関数」と「微分係数」の2つの語の使い分けは必要であり重要であるとも言えます。
ところで接線の傾きが分かれば「接線を表す直線の式」も関数として分かる事になります。
x=aにおける微分係数をf'(a)と書くとするとその点での接線の式は
f(x)-f(a)=(x-a)f'(a)であり、
本来「微分」とはむしろそのような接線の式を指して呼ぶという考え方もあります。
この考え方のもとでは、
接線の式の左辺をdyと書き右辺のx-a の部分をdxと書く事があります。
すると接線の式はdy=dxf’ (a)のようになります。
つまり接線の式を指して微分と呼ぶ考え方は、接点を原点とした新たな1次式(直線の式)においてxの変化分dxに対するyの変化分dyを指して「微分」と呼んでいるわけです。
(この場合、置き換えをしているだけなのでdyやdxは必ずしも微小量とは限りません。)
この考え方のもとでは「割り算としてのdy/dx」は微分係数f'(a)に等しい事になり、物理等では微小量においての考察でこれにかなり近い考え方が使われる事があります。
ただしその考え方のもとでも「dy/dx」という記号は1つの塊として導関数f'(x)を指し、「微分する」と言えば微分演算の事を指します。
微小なxとyの変化分の割り算を考えて、極限をとる事で微分演算とする考え方は微分の定義式の1つでもあります。しかし、記号としては割り算を行う時にdyやdxを使う事はなるべく避けられて、代わりにΔy(「デルタy」)やΔxの記号が使用される事が多いです。
微分の定義式
微分の定義式は、次のように極限の形式になっています。
この定義式を使う事により、各種の微分公式を導出する事ができます。
■2点間の変化率(傾き)の極限値としての微分の定義
【次式の極限値が存在する時、それが f(x) の導関数。】
$$f^{\prime}(x)=\lim_{a \to x}\frac{f(x)-f(a)}{x-a}$$
■x-a=hとおいた表記
【各種の微分の公式を導出する時にはこれが便利です。】
$$f^{\prime}(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$
■x-a =Δxと書いて,f(x)-f(a)=Δyと書いた時の表記
【文章中で表記を簡易的に済ませたい時に便利な事もあります。】
$$f^{\prime}(x)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}$$
ΔxとΔyを「増分」と呼ぶ事もありますが、マイナスの値の時もあります
特にΔyは、xの増加に対して減少して行く関数では普通にマイナスの値を取り得ます。
また、ΔxとΔyという記号は「微小な変化量」の意味で使われる事も多いです。
また、微分係数は導関数が存在する場合にxに具体的な値を当てはめる事でも計算できますが、上記の定義式とほぼ同じ形を使って書く事も一応可能です。
例えば関数y=f(x)のx=x1における微分係数は次の式で書く事もできます。
$$x=x_1における微分係数:f^{\prime}(x_1)==\lim_{a \to x_1}\frac{f(x_1)-f(a)}{x_1-a}$$
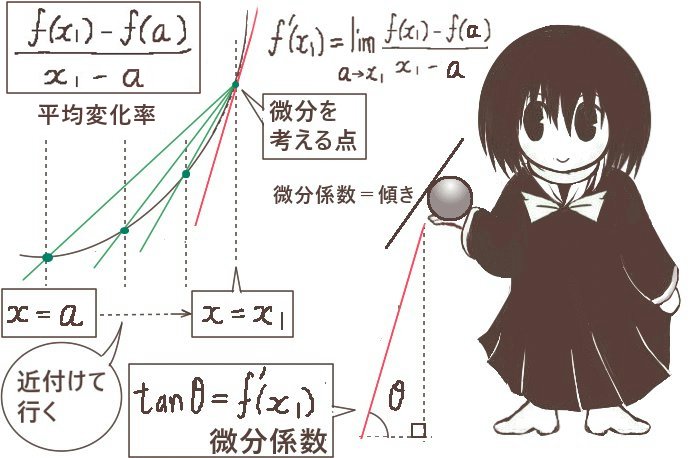
微分の定義式において、極限を考えている対象の式{f(x)-f(a)}/(x-a) を関数y=f(x)の「平均変化率」と呼ぶ事もあります。その観点からは微分は、平均変化率を限りなく短い区間で考えた極限値であると言う事もできます。
微分の表記方法
微分を表す記号は大きく分けて3種類が使われていて、
①関数を表す文字の右上に「 ’ 」の記号【プライムあるいはダッシュ】を付けるか、
②微分演算子 \(\frac{\Large d}{\Large dx}\)(文章中での略記:d/dx)を関数に作用させるか、
③あるいは関数を表す文字の上に「・」【ドット】を付けるかで表します。
具体的にy=sinxやy=x2+xといった関数や、より一般的にy=f(x)で表される関数に対する微分は次のような表記で書かれます。
| 関数 | 表記の例(いずれも意味は同じ) | 備考 |
| y=sinx | \(y^{\prime}\) \((\sin x)^{\prime}\) \(\frac{\Large dy}{\Large dx}\) \(\frac{\Large d}{\Large dx}(\sin x)\) \(\dot{y}\) | y’ 表記は「xによる微分」 である事が明確な時に使用。 |
| x2+x | \((x^2+x)^{\prime}\) \(\frac{\Large d}{\Large dx}(x^2+x)\) | \((x^2)^{\prime}+x^{\prime}\)および \(\frac{\large d}{\large dx}(x^2)+\frac{\large d}{\large dx}x\)に等しい |
| y=f(x) | \(f^{\prime}(x)\) \(\frac{\Large df}{\Large dx}\) \(\frac{\Large df(x)}{\Large dx}\) \(\frac{\Large d}{\Large dx}f(x)\) | f(x)に対するドット表記\(\dot{f}\)や\(\dot{f}(x)\) は、あまり使われない。 |
f’(x)は「fプライムx」「fダッシュx」のように読んだりします。
dy/dxなどの記号はそのまま「ディーワイディーエックス」などと読まれて、
\(\dot{y}\) は「ワイドット」のように読まれる事があります。
数学史的にはdy/dx型の表記はライプニッツが使っていたとされる表記で、
ドットによる表記はニュートンが使用していたというのが通説です。
導関数をy’ あるいはf’(x)で表す表記は「y=f(x)というxを変数とする関数があり、xで微分演算を行う」という事が明確である場合に便利な表記です。
微分演算子を使う表記では、変数がxではない場合には変数の部分の記号を変えて使用します。例えばtによる関数y=t2を微分する時にはxではなくtで微分するのでdy/dt,d/dt(t2)のように表記します。言い換えると、微分演算子による微分の表記は「何の変数で微分しているのか」を明確にできます。
ドットを使った表記は主に物理で使用されて、微分した後にさらに2乗するだとか、その他式が複雑になる時に表記上便利です。例えば導関数の2乗を使う式の場合、(dy/dx)2といった表記を長い式の中で何度も繰り返すのは大変ですが、\(\dot{y}^2\) の表記なら比較的簡単に済む場合があります。
微分の表記としてドットを使う場合の使用例としては、サイト内記事で取り扱っている例としては少々複雑な計算ですが古典力学における運動方程式を極座標系の成分で書き直すための計算などがあります。その例では時間tを変数とした微分を考えています。
微分の四則演算
2つの関数f(x)とg(x)をそれぞれf,gと略記します。またcは定数であるとします。
定義式から、
f+g【関数の和】,f-g【関数の差】、cf【関数の定数倍】に対する微分は
それぞれ次のように計算できます。
- (f+g) ‘=f’+g’
- (f-g) ‘=f’-g’
- (cf) ‘=cf’
あるいは、3式をまとめて
(c1f±c2g) ‘=c1f’±c2g’
のようにも表現できます。
これらの演算は、定義式に当てはめて丁寧に計算すると証明する事ができます。
(証明は比較的容易ですが、「自明」な事実では無い事に注意は必要です。)
具体的には、例えばx2+x+1のような多項式の微分は
(x2+x+1) ‘=(x2) ‘+(x) ‘+(1) ‘=2x+1+0=2x+1
のように計算してよい事を意味します。
これは地味ですが微分を利用していくうえで非常に重要な公式であるとも言えます。

他方で、関数同士の積fgや商f/gに対する微分は少し妙な形の公式である
(fg) ‘=f’g+fg’ および (f/g) ‘=(f’g-fg’ )/(g2)
が成立します。これら2式も微分の定義式から証明できます。
微分不可能な場合とは
微分の定義式を見ると極限の形になっています。その極限値が存在するなら導関数として扱えるという事であり、極限値が存在しない(収束しない)場合には導関数を表せません。
そのような時、関数は微分不可能であると言います。
また、極限の計算自体は一応できても導関数や微分係数が1つの形に定まらない場合も同様に微分不可能とみなす事が普通です。
逆に導関数が存在する時には微分可能である(もしくは可微分である)と言います。
定義域内のほとんどの点では微分可能であっても、ある特定の点でだけ微分不可能という場合もあります。そのような場合には「例えばx=0では微分不可能」といったようにその特定の点での微分係数を式で表現できない事を表します。
微分可能であるか微分不可能であるかどうかという事を指して微分可能性とも言います。用語としては「x=0における微分可能性を調べてみると、・・・」のように使います。
初等関数では定義域内のほとんどの点で微分可能であり、
一部の点が微分不可能になっている場合があります。
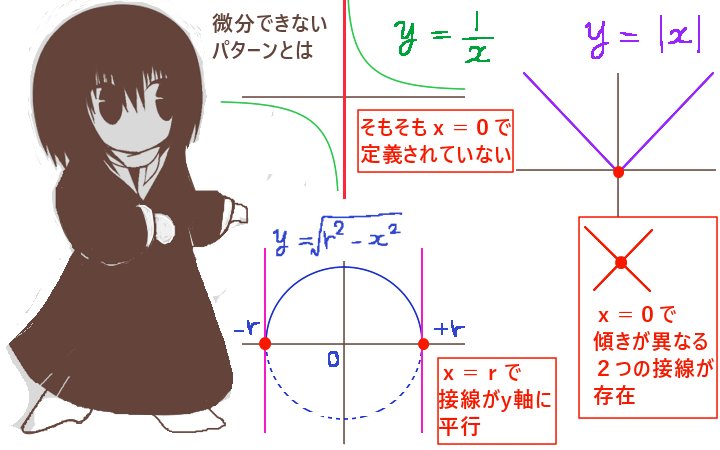
そもそも定義されていない点
関数y=1/xの「x=0の点」や、正接関数y=tanxの「x=π/2の点」のように、そもそも関数を定義できない点では図形的に接線を引く事もできず、数式的に微分をする事もできません。
それらの点に対して導関数の極限を考える事は可能ですが、反比例の関数や正接関数ではその極限も無限大に発散します。図形的には、そのような点に向かって接線は限りなくy軸に平行な直線に近付いていく事になります。
関数は定義できても導関数だと定義できなくなる領域
考えている点で関数が定義されていても微分できない点が存在する場合もあります。
そのような場合の1つは、もとの関数では定義が可能であっても導関数を計算すると不連続点が発生して微分係数が無限大に発散する場合です。図形的に見ると、大抵はその点での接線はx軸に垂直でy軸に平行になっています。つまり傾きで言うと「無限大」になっている状況です。
この状況を「微分係数が∞(無限大)である」と考える事はできなくは無いですが、基本的にはその時には微分の定義式で極限が収束せず無限大に発散するので微分係数は存在しないと考えます。
具体的には、円を座標上の関数として考えた場合や、xの平方根に対してそのような点が存在します。例えばxの平方根は、もとの関数ではx=0での関数値が存在します。しかし微分して得られる導関数はx=0で無限大になり定義できない事が分かります。
| 関数 | 導関数 | 微分可能性 |
| \(y=\sqrt{x}\) 【定義域:x≧0】 | \(y=\frac{\Large 1}{\Large 2\sqrt{x}}\) 【定義域:x>0】 | x=0:微分不可能 x>0:微分可能 |
| \(y=\sqrt{r^2-x^2}\) 【-r≦x≦r】 (原点が中心の半円) | \(y=-\frac{\Large x}{\Large \sqrt{r^2-x^2}}\) 【定義域:-r<x<r】 | x=±r:微分不可能 -r<x<r:微分可能 |
同じ点で微分係数が2つの異なる値をとる場合
微分の定義式を計算すると極限値が有限の値として存在するけれども、詳しく見ると「値が2通り存在してしまい、1つの値に定まらない」という場合があります。このような場合にもその点では微分不可能であると考えるのが一般的です。
具体的にはy=|x|のような関数が該当します。
これはx≧0の時y=x,x<0の時y=-xという関数であり、
場合分けをして定義するような種類の関数です。
この関数は「x=0で微分不可能、その他の区間では微分可能」になります。
これは図形的に見れば直線を組み合わせた形をしているので微分の定義から計算をしなくても「接線」の傾きはそのまま直線の傾きになります。
そこでx=0での微分可能性を見てみると、「接線」は引く事ができてしかも有限の値であるけれども、傾きは+1と-1の両方があり得てしまう事が分かります。このような時には、x=0での微分係数は「値が1つに定まらない」という意味で微分不可能であると考える事が一般的なのです。
この事は、極限一般の観点から言うとh→0の極限は「hをプラスの値に保ったまま0に近付ける」時と「hをマイナスの値に保ったまま0に近付ける」時とで極限値が変わってしまう事がある場合に該当します。前者を右側極限と呼び、後者を左側極限と呼ぶ事もあります。
- 右側極限:hをプラスの値に保ったまま0に近付ける。「h→+0」とも書く
- 左側極限:hをマイナスの値に保ったまま0に近付ける。「h→-0」とも書く
- y=|x| では、x=0における微分の計算で右側極限と左側極限の値が一致しない。
一般的に「微分可能である」という事は微分の定義式の極限において右側極限と左側極限の値が一致する場合のみ、という判定をします。y=|x|のような場合分けを含まない初等関数では、定義できない点がある場合は除外して考える限りにおいては、右側極限と左側極限の一致・不一致の問題は微分計算でそれほど気にする必要は無いと言えます。
y=|x| に対するx=0における微分については、右側極限と左側極限のそれぞれが無限大に発散するわけでは無い事を考慮して「右側微分可能」かつ「左側微分可能」であるけれども「微分は不可能」であると表現する事もあります。