物理学などでは、微分方程式を座標変換して考える時があります。
例えば極座標における運動方程式や波動方程式を考えてみるといった事です。
そのような場合で特にベクトルを含む微分方程式を考える時には、
x=rcosθ等の関係の代入だけでなくベクトルの基本ベクトルを変更する事まで行う事があります。
普通はベクトルを成分で表す時には(x座標,y座標,z座標)で考えるわけですが、
それを(r座標,θ座標,φ座標)で表す事を意味します。
例えば運動方程式であれば加速度ベクトルや力ベクトルをそのように扱うという事です。
以下、微分も使いながら具体的な変換の方法などを詳しく説明します。
■この記事に特に関連が深い数学的な事項は方向余弦に関する内容と、極座標および球面座標に関する内容です。その他、記事の後半では微分に関する基本公式のいくつかを使用しています。ベクトルと三角関数に関する基本的な事項も使います。
基本ベクトルの変更をする必要がある場合と無い場合
極座標変換等をする場合の微分方程式については、
基本ベクトルを変更する必要がある場合と無い場合があります。
まず、変更の必要が無い場合を見てみましょう。
例えば「等速円運動をしている物体には常に中心力が働いている」という事を
運動方程式を使って示そうとするような場合です。
この時には物体の座標に対して極座標変換を行ってから時間微分を2回行って、
普通に運動方程式に当てはめて力ベクトルを計算する事には何の問題もありません。
このような場合は、極座標変換を使っていても基本ベクトルの変更が必要ない場合です。
少しややこしいようですがそのような場合には、
「x=rcos(ωt) のような極座標変換は確かに行ってはいるけれども、
ベクトルの座標成分としては直交座標によるものを考えている」のです。
ですので極座標による値によって計算をするとしても、
その結果は「xyz直交座標系のx軸で測った値」を出しているわけです。
もう少し詳しく見ると、そのような場合には極座標変換を使用していますがベクトルとして考えている加速度ベクトルや力ベクトルは成分を「x成分」「y成分」「z成分」として考えています。図的にはx軸、y軸、z軸に平行なベクトルの合計として1つの加速度ベクトルや力ベクトルを構成します。
では、加速度や力のベクトルを直交座標ではない成分表示で「r成分」「θ成分」「φ成分」のように表して、図的にも「ある点での曲線の接線方向」を向いたベクトルの合計として1つの加速度ベクトルや力ベクトルを構成できるのか?
という事を考えると、結論を言うと「それは可能である」という事になるのです。
そのような場合の運動方程式は「力が質量と加速度に比例する」という関係は直交座標の時と同じですが、成分ごとに見るとある曲線の接線方向の加速度成分と力の成分を考える事になるわけです。
そのように考える時の具体的なベクトルの成分の変換方法を以下述べていきますが、
一般の曲線座標系への変換は話が複雑過ぎるので、物理学等で使われる事があって数学的にも比較的話が穏やかで済む直交曲線座標系への変換に限定して話を進めていきます。
(と言っても、それでも多少複雑になります。)
直交曲線座標とは、聞き慣れない事も多いかと思いますが
具体的には極座標や球面座標、円柱座標のようなものを指します。
これらの座標系では、座標軸に相当する「座標曲線」が任意の点で直交します。
通常のxyzの直交座標系も、直交曲線座標系の特別な場合であるという見方もできます。

他方で、物理の法則を数式で表す時に座標系ごとに形を変換しないといけないというのでは一般論として議論する時に不便であるという考え方があります。
その考え方のもとで、変分原理による計算で導出する「座標系に依存しない運動方程式等の形」というものも存在します。(ラグランジュ型の運動方程式などとも呼ばれます。)
力学の分野である「解析力学」では、そのような考察を計算によって行います。
基本ベクトルと成分の直交曲線座標系への変換方法
ベクトルを含む微分方程式を座標系ごとの形に変換する時に、まず第一に重要となるのがベクトルを構成する基本ベクトルに対する成分の変換方法です。ここではその具体的な方法について説明します。
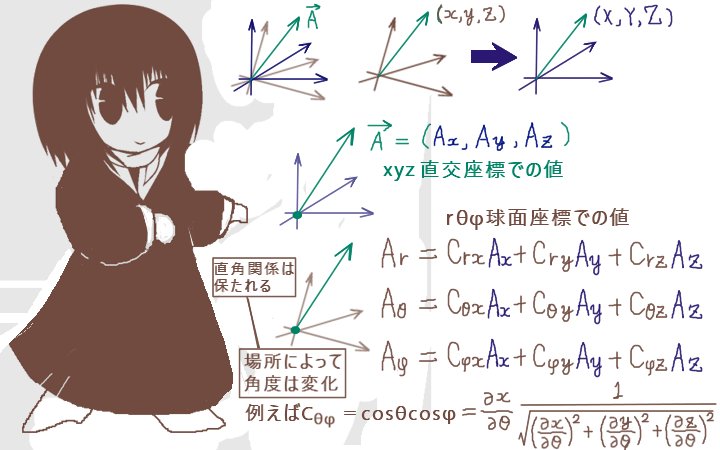
直交座標上のベクトルは、
(1,0,0)と(0,1,0)と(0,0,1)という
3つの基本ベクトルの線形結合で表す事ができます。
それらをそれぞれ\(\overrightarrow{e_x}\),\(\overrightarrow{e_y}\),\(\overrightarrow{e_z}\) と表す事にすると
任意のベクトルは実数a,b,cを使って\(\overrightarrow{A}=a\overrightarrow{e_x}+b\overrightarrow{e_y}+c\overrightarrow{e_z}\)と書けます。
そして、ここで使った実数a,b,cはそれぞれベクトルの成分であるわけです。
(数学の理論上はこれらの成分は複素数を使っても可です。)
曲線座標でも実は同じような考え方ができて、直交座標からの変換を考える時は基本ベクトルは「向きが座標曲線の勾配ベクトルである単位ベクトル」であり、ここで言う勾配ベクトルはx,y,zで考えたものを指しています。
【■参考:ベクトル解析の概論の記事(勾配ベクトルの微分による定義など)】
より具体的には1つの座標曲線をxyz直交座標でu=F(x,y,z)で表せるとして grad u により表されますが、実際に直交曲線座標で考える時には「r方向」「θ方向」「φ方向」といった形で図形的に把握していればよい事も多いと言えます。そこで、曲線座標における基本ベクトル \(\overrightarrow{e_r}\),\(\overrightarrow{e_\theta}\),\(\overrightarrow{e_{φ}}\) は分かっているものとして次に成分のほうを考えます。
| 直交座標系 | 曲線座標系 |
| $$\large{\overrightarrow{A}=A_x\overrightarrow{e_x}+A_y\overrightarrow{e_y}+A_z\overrightarrow{e_z}}$$ | $$\large{\overrightarrow{A}=A_r\overrightarrow{e_r}+A_{\theta}\overrightarrow{e_\theta}+A_{φ}\overrightarrow{e_φ}}$$ |
ここで、曲線座標系が直交曲線座標であるならば
ベクトルの成分の変換は局所的には方向余弦を使った線形結合の形で表す事ができます。
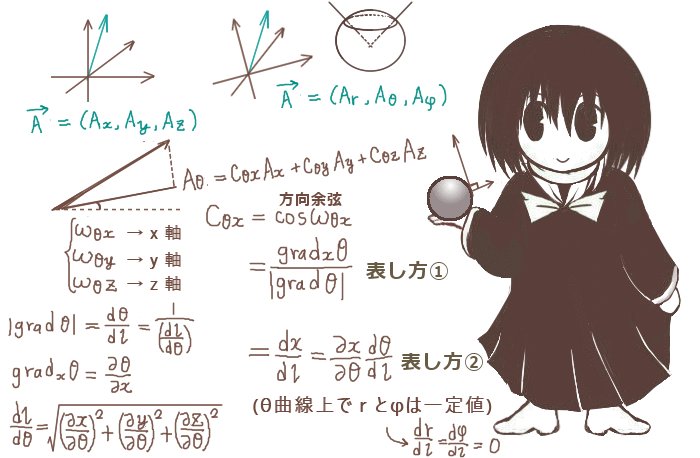
方向余弦とはその名の通り三角関数の cosθの形で表される量ですが、ここでは角度の値はあまり重要でないのでCの文字と添え字を使って表す事にします。
直交曲線座標系の3つの各基本ベクトルからの、直交座標系のx軸、y軸、z軸への9つの方向余弦を次のようにここでは表記します。
| ここでの方向余弦の 記号の表 | x軸に対して | y軸に対して | z軸に対する |
| r曲線の基本ベクトル \(\overrightarrow{e_r}\)から | Crx | Cry | Crz |
| θ曲線の基本ベクトル \(\overrightarrow{e_\theta}\)から | Cθx | Cθy | Cθz |
| φ曲線の基本ベクトル \(\overrightarrow{e_{φ}}\)から | Cφx | Cφy | Cφz |
これらの方向余弦を使う事で、各点における基本ベクトルと個々のベクトルの成分を直交曲線座標系のものに変換できます。
上記の9つの方向余弦と、xyz直交座標系での成分を使う事で
直交曲線座標系でのベクトルの3つの成分は次のように表されます。
$$\large{A_r=C_{rx}A_x+C_{ry}A_y+C_{rz}A_z}$$
$$\large{A_{\theta} =C_{\theta x}A_x+C_{\theta y}A_y+C_{\theta z}A_z}$$
$$\large{A_φ=C_{φx}A_x+C_{φy}A_y+C_{φz}A_z}$$
この式は、元々は「原点を共有する2つの直交座標におけるベクトルの成分の変換公式」です。
ただし直交曲線座標では基本ベクトルとなる3つのベクトルが互いに直交するので、
各点での方向余弦を関数として表すという前提のもと、同じ変換公式を適用できます。
そこで次は、これらの方向余弦は具体的にどのような数式で表されるのかが問題になります。
それが分れば一般の変換公式を作れるわけです。
変換で使う「方向余弦」を微分により表す公式
方向余弦とは基本的には「余弦」なので「底辺/斜辺」の関係を使います。ただし基本ベクトルは座標曲線の接線ベクトルとして考えていますから方向余弦も微分や偏微分で考える必要があります。また、直交曲線座標系の基本ベクトルからxyz直交座標系の軸への方向余弦の表し方は実は2つあって、どちらを使っても同じ結果を得ます。
座標曲線をu,v,wとして、u=u(x,y,z)に対する
j軸(x,y,z軸のいずれか)の方向余弦は、
u の弧長をl(u)とした時に
次の2通りの表し方があります。
■勾配ベクトル(xyz直交座標系で表したもの)を使う方法
勾配ベクトルは grad u=(∂u/∂x,∂u/∂y,∂u/∂z)で表されるベクトルであり
(ナブラ記号を使うと grad u=∇u)、gradj uは勾配ベクトルのj成分で∂u/∂jの事です。
直交曲線座標系で成立する|gradu|=du/dlの関係式も使っています(証明と説明は後述)。lはu曲線の弧長で、「u増加する向き」にlが増える方向で考えます。(その時du/dl≧0)
$$
C_{uj}=\frac{\mathrm{grad}_ju}{|\mathrm{grad}u|}=\frac{dl}{du}\frac{\partial u }{\partial j}
$$
■弧長を斜辺とする方法
(u曲線上では、他の座標曲線の変数は一定でdv/dl=0およびdw/dl=0)
$$
C_{uj}=\frac{dj}{dl}=\frac{\partial j}{\partial u}\frac{du}{dl}+\frac{\partial j}{\partial v}\frac{dv}{dl}+\frac{\partial j}{\partial w}\frac{dw}{dl}$$
$$
=\frac{\partial j}{\partial u}\frac{du}{dl}$$
弧長に対するuによる微分での導関数dl/duは次のように表されます。
$$\frac{dl}{du}=\sqrt{\left(\frac{\partial x}{\partial u}\right)^2+\left(\frac{\partial y}{\partial u}\right)^2+\left(\frac{\partial z}{\partial u}\right)^2}$$
また、dl/duは1変数の導関数なのでdu/dlを次のように表せます。
(逆関数の微分公式によります。)
$$\frac{du}{dl}=\frac{1}{\Large{\frac{dl}{du}}}=\frac{1}{\large{\sqrt{\left(\frac{\partial x}{\partial u}\right)^2+\left(\frac{\partial y}{\partial u}\right)^2+\left(\frac{\partial z}{\partial u}\right)^2}}}$$
極座標や球面座標への基本ベクトルおよび成分の変換を行う時には
具体的にはx=rcosθなどと表す事から∂x/∂θなどが計算しやすい場合が多くあります。その時には上記の「弧長を斜辺とする方法」を使ったほうが比較的分かりやすくなります。(この記事の後半でもそちらの形の公式を使用。)
dl/dθ や dθ/dlを表す事になる弧長の式については、次に見て行くように球面座標であればr,θ,φの3つ分計算しておく必要があります。平面の極座標であればrとθの2つ分です。
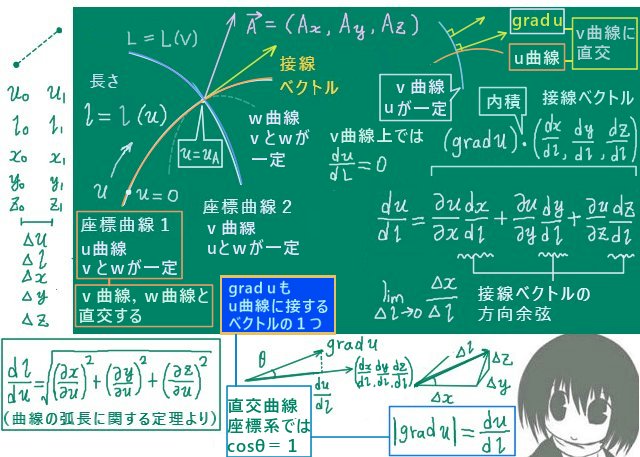
曲線の弧長については元々は定積分で次のように書く事ができて、
上記ではそれを微分した導関数を使用しています。$$l(u)=\int_0^u\sqrt{\left(\frac{\partial x}{\partial u}\right)^2+\left(\frac{\partial y}{\partial u}\right)^2+\left(\frac{\partial z}{\partial u}\right)^2}dt$$
微分は、ここでの変数で言うとuで行います。
この式は曲線を折れ線に近似して図的に見る事でも理解可能ですが、解析学的に証明もできる式です。
同じ方向余弦の表し方が2つ存在する事と、
|grad u|=du/dlの関係式についての証明と説明
勾配ベクトルについて一般的に成立するのは、スカラー場の値が一定値となっている「等位面」に対して必ず垂直であるというものです。(以下、等位面に含まれる曲線を「等位線」と呼んでおきます。)
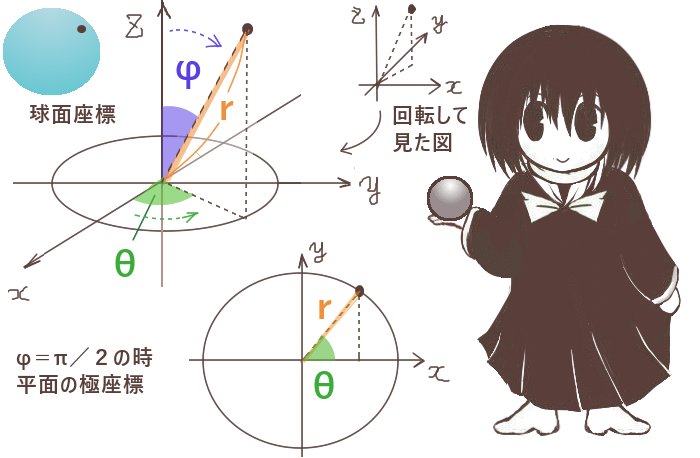
極座標のθ曲線である「原点を中心とする同心円」の円周上では
半径が一定であり同心円は「rが一定値である等位線」を構成しています。
球面座標ではrが一定値の球面が等位面として存在します。
スカラー関数F(x,y,z)と弧長がlで表される曲線があるとして、曲線上の座標を成分とするベクトルを\(\overrightarrow{r}=(x(l),y(l),z(l))\)とします。
曲線上でdF/dlを計算すると次式になります。(合成関数に対する偏微分の公式を使用。)$$\frac{dF}{dl}=\frac{\partial F}{\partial x}\frac{dx}{dl}+\frac{\partial F}{\partial y}\frac{dy}{dl}+\frac{\partial F}{\partial z}\frac{dz}{dl}=(\mathrm{grad}F)\cdot\frac{d\overrightarrow{r}}{dl}$$
$$ここでもし\frac{dF}{dl}=0であるなら、(\mathrm{grad}F)\cdot\frac{d\overrightarrow{r}}{dl}=0$$
つまり「Fの値が変化しない曲線」=「Fの等位線」においては
「Fの勾配ベクトルは曲線の接線ベクトルに常に垂直」という事になります。
ところで、直交曲線座標においては1つの座標曲線上では他の変数の値が一定であり、r曲線とφ曲線上でθは一定値です。
また、θ曲線上の任意の点ではr曲線およびφ曲線との交点が存在します。
【より詳しく言えばこれらの曲線は「曲面」を構成しています。】
ところで直交曲線座標系であればr曲線およびφ曲線はθ曲線との交点で直交します。
これは具体的には任意の点での「曲線の接線ベクトル」同士が直交するという意味です。
先ほどの考察から、勾配ベクトル gradθ は
「θが一定値であるφ曲線およびθ曲線上の任意の点」での接線ベクトルに直交します。
よって、gradθ はu曲線上の任意の点において、その点でu曲線と交わるφ曲線およびθ曲線に直交しています。
そして、u曲線自体もφ曲線およびθ曲線に直交しているのでした。
という事はその点においてu曲線の接線ベクトルとgradθは平行なベクトルである事になり、それはすなわちgradθがその点におけるθ曲線の接するベクトルの1つである事を示しています。
先ほどのdF/dlの式においてFの代わりにθを考えると
$$\frac{d\theta}{dl}=\frac{\partial \theta}{\partial x}\frac{dx}{dl}+\frac{\partial \theta}{\partial y}\frac{dy}{dl}+\frac{\partial \theta}{\partial z}\frac{dz}{dl}=(\mathrm{grad}\theta)\cdot\left(\frac{dx}{dl},\hspace{2pt}\frac{dy}{dl},\hspace{2pt}\frac{dz}{dl}\right)$$
と表せるわけですが
dx/dl等は、大きさがΔlであるベクトル(Δx,Δy,Δz)における
方向余弦
であるΔx/ΔlのΔl→0の極限値でもあります。
すると、方向余弦についての関係式により、
θ曲線の接線ベクトル(dx/dl,dy/dl.dz/dl)方向の
gradθの成分はdθ/dlである事になります。
よって、何らかの余弦cosω()を使って|gradθ|cosω=dθ/dlと表せる事になりますが、
θ曲線の接線ベクトルと gradθは同じ点でθ曲線に接するのでcosωの値は1か-1です。
上式でF=u(x,y,z)で表す場合【より正確にはこれは曲面を表します】には、弧長であるlは「u増加する向きにlが増えて行く方向」で考えます。
そのためdu/dl ≧0であるので、
cosω=1であり(-1ではなく、という意味)|gradθ|=dθ/dl
するとgradθとθ曲線の接線ベクトルは同じ向きのベクトルであるのでx軸,y軸,z軸への方向余弦は「直角三角形の底辺/斜辺」=「直交座標系でのベクトルの成分/ベクトルの大きさ」として同じ値を持ちます。
(向きは同じでも、ベクトルの大きさは異なります。|gradθ|=dθ/dlですがこれは接線ベクトルの大きさとは一般的に異なります。)
以上の事は直交曲線座標系の任意のu曲線で成立します。
補足として、ベクトルの「方向余弦」自体は余弦 cosθ であるので、軸に対する向きが同じであれば大きさはどのようなベクトルであっても底辺/斜辺の関係で方向余弦を表す事ができます。
つまり数学的には1つの方向余弦の表し方は無限にあるわけですが、ここでの一般的な変換に使えるような微分による方向余弦の表し方の方法としては上記の2通りがあるという事になります。
変換の具体例1(平面の極座標変換の場合)
ベクトルの基本ベクトルと成分に対して具体的に平面での極座標変換をしてみます。平面なので必要な方向余弦は4つで、それを表すために偏微分が4つと弧長の式が2つ必要になります。
まず、xとyに対するrとθの偏微分です。
| 極座標変換の時 | ∂/∂r | ∂/∂θ |
| x=rcosθ | cosθ | -rsinθ |
| y=rsinθ | sinθ | rcosθ |
次に弧長の計算です。∂x/∂rなどを計算してあるので、公式に代入します。
dr/dlなどを使う事になりますが、まずはdl/drの形で記しておきます。
$$\frac{dl}{dr}=\sqrt{(\cos\theta)^2+(\sin\theta)^2}=1$$
$$\frac{dl}{d\theta}=\sqrt{(-r\sin\theta)^2+(-\cos\theta)^2}=\sqrt{r^2}=r$$
このように意外と簡単な式になります。
さらに、θのほうの弧長の式で出てきたrは∂x/∂θの式にあるrと打ち消して方向余弦の値には含まれなくなります。(そのように計算が簡単になる事は一般的に保証されるわけではありませんが、球面座標の場合でも同じ事が起こります。)
方向余弦はCrx=(∂x/∂r)・(dr/dl)=cosθ のように計算します。
θについては例えばCθx=(∂x/∂θ)・(dr/dl)=(-rsinθ)・(1/r)=-sinθです。
先ほど述べたようにrは打ち消して式から無くなるわけです。
4つの方向余弦は具体的には次のような形になります。
- Crx=(∂x/∂r)・(dr/dl)=cosθ
- Cry=(∂x/∂r)・(dr/dl)=sinθ
- Cθx=(∂x/∂r)・(dr/dl)=-sinθ
- Cθy=(∂x/∂r)・(dr/dl)=cosθ
よってrθ極座標系での基本ベクトルでの\(\overrightarrow{A}\)の成分は
Ar=CrxAx+CryAy=Axcosθ-Aysinθ
Aθ=CθxAx+CθyAy=Axsinθ+Aycosθ であり、
\(\overrightarrow{A}\)=(Axcosθ-AysinθAθ ,Axsinθ+Aycosθ)となります。
ところでこれらについて運動方程式等に適用するために微分を考える場合などはどうなるのか?という事については後述します。時間微分に関しては得られた変換の結果の式をそのままtで微分すればよいのですが、元の座標系の値であるAxに関する処理が必要となります。
xy直交座標系からrθ極座標系に基本ベクトルと成分を変換する式は次のようになります。
$$A_r=\hspace{7pt}A_x\cos\theta+A_y\sin\theta$$
$$A_{\theta}=-A_x\sin\theta+A_y\cos\theta$$
平面極座標への変換の場合には、直交座標を原点回りに回転させる形で
各点での局所的な変換を行うものとして図から導出する事もできます。
変換の具体例2(球面座標変換の場合)
次に球面座標の場合を見てみます。角度のとりかたはθとφの2箇所がありますが、ここでは平面極座標との関連を見やすくするためにθをxy平面での角度にとり、Φをr曲線(と言っても直線ですが)とz軸のなす角にとって考えます。
9つの偏微分と3つの弧長をまとめると次の通りです。
| 球面座標変換の時 | ∂/∂r | ∂/∂θ | ∂/∂φ |
| x=rsinφcosθ | sinφcosθ | -rsinφsinθ | rcosφcosθ |
| y=rsinφsinθ | sinφsinθ | rsinφcosθ | rcosφsinθ |
| z=rcosφ | cosφ | 0 | -rsinφ |
| 弧長 | 式 | 逆数(dr/dlなど) |
| dl/dr | 1 | 1 |
| dl/dθ | rsinφ | 1/(rsinφ) |
| dl/dΦ | r | 1/r |
弧長の式に関する具体的な計算は次のようになります。 $$\frac{dl}{dr}=\sqrt{\left(\frac{\partial x}{\partial r}\right)^2+\left(\frac{\partial y}{\partial r}\right)^2+\left(\frac{\partial z}{\partial r}\right)^2}=\sqrt{(\sin φ\cos\theta)^2+(\sinφ\sin\theta)^2+(\cos φ)^2}$$ $$=\sqrt{\sin^2φ(\cos^2\theta+\sin^2\theta)+\cos^2φ}=\sqrt{\sin^2φ+\cos^2φ}=1\hspace{60pt}$$ $$\frac{dl}{d\theta}=\sqrt{\left(\frac{\partial x}{\partial \theta}\right)^2+\left(\frac{\partial y}{\partial \theta}\right)^2+\left(\frac{\partial z}{\partial \theta}\right)^2} =\sqrt{(r\sin φ\sin\theta)^2+(r\sinφ\cos\theta)^2+0^2}\hspace{15pt}$$ $$=\sqrt{r^2\sin^2φ(\sin^2\theta+\cos^2\theta)}=\sqrt{r^2\sin^2φ}=r\sin φ\hspace{105pt}$$ $$\frac{dl}{dφ}=\sqrt{\left(\frac{\partial x}{\partial φ}\right)^2+\left(\frac{\partial y}{\partial φ}\right)^2+\left(\frac{\partial z}{\partial φ}\right)^2}\hspace{200pt}$$ $$ =\sqrt{(r\cos φ\cos\theta)^2+(r\cosφ\sin\theta)^2+(r\sin φ)^2}\hspace{115pt}$$ $$=\sqrt{r^2\cos^2φ(\cos^2\theta+\sin^2\theta)+r^2\sin^2 φ}=\sqrt{r^2(\cos^2φ+\sin^2φ)}=\sqrt{r^2}=r\hspace{0pt}$$ dl/dθの計算では、角度φは正弦sinφが0以上の値をとる範囲で考えるとします。それは0≦φ≦πの範囲になりますが、図的に見てもその範囲だけで考えても十分である事になります。それは球面座標においてはθの変化もあるからです。
以下、上記の結果と公式を適用して計算をしていく事で
基本ベクトルを直交座標から球面座標に変換した時のベクトルの変換の公式を得ます。
$$
方向余弦の式\hspace{5pt}C_{uj}=\frac{\partial j}{\partial u}\frac{du}{dl}\hspace{5pt}【u=r,\theta,φ\hspace{3pt}j=x,y,z】$$
$$(具体例)C_{\theta y}=\frac{\partial y}{\partial \theta}\frac{d\theta}{dl}=(r\sinφ\cos\theta)\cdot\frac{1}{r\sinφ}=r\cos\theta$$
| 方向余弦 | x軸 | y軸 | z軸 |
| r 曲線 | Crx=sinφcosθ | Cry=sinφsinθ | Crz=cosφ |
| θ 曲線 | Cθx=-sinθ | Cθy=cosθ | Cθz=0 |
| φ 曲線 | Cφx=cosφcosθ | Cφy=cosφsinθ | Cφz=-sinφ |
| r 成分 | Ar= | CrxAx+CryAy+CrzAz | = Axsinφcosθ+Aysinφsinθ+Azcosφ |
| θ 成分 | Aθ= | CθxAx+CθyAy+CθzAz | =-Axsinθ+Aycosθ |
| φ 成分 | Aφ= | CφxAx+CφyAy+CφzAz | = Axcosφcosθ+Aycosφsinθ-Azsinφ |
φ=π/2の時、すなわちr曲線が常にxy平面にある時には
sinφ=1および cosφ=0を代入し、
さらにもとの直交座標でz成分Az=0とすれば平面極座標の時の変換公式になります。
(θ成分への変換式はφもAzも含んでおらず、実は極座標の時と同じ式です。)
これらの式は
「xy平面での角度をΦとしてz軸とr曲線のなす角をθとした場合」には、
θとφを入れ換える事になります。
| r 成分 | Ar= | CrxAx+CryAy+CrzAz | = Axsinθcosφ +Aysinθsinφ +Azcosθ |
| φ 成分 | Aφ= | CφxAx+CφyAy+CφzAz | =-Axsinφ+Aycosφ |
| θ 成分 | Aθ= | CθxAx+CθyAy+CθzAz | = Axcosθcosφ+Aycosθsinφ-Azsinθ |
これらの式は単なるθとφの文字の置き換えをしただけであり、
何か新しい変換を行ったという事ではありません。
図のφ=π/2と合わせて「ベクトルのφ成分の時間微分が0である」という条件も考えると一般論としての球面座標から移行を考える事ができます。
運動方程式の球面座標系での成分表示の導出
各成分に対する時間微分を考える時には、直交座標での「ベクトルの時間微分」を1つのベクトルと考えて上記の変換公式を適用します。考え方は、1階の微分でも2階の微分でも同じになります。
- 直交座標の成分に対する時間微分dAx/dtなどを計算します。
(2階微分をする時はd2Ax/dt2を計算します。)
ただし、計算結果は変換後の変数であるrやθで表す必要があります。 - ベクトルの時間微分(d/dt)\(\overrightarrow{A}\) は1つのベクトルであるので、変換の公式を適用して基本ベクトルの変換を行います。
- 変換の式に含まれる「直交座標で考えた時の成分」に、直交座標で考えた時間微分dAx/dtなどを代入します。
一番簡単な例(と言っても多少複雑ですが)で、
尚且つ重要なベクトルは物体の位置を表す\(\overrightarrow{r}\)=(x,y,z)です。
何の断り書きもなければ直交座標の成分で表されています。
次に、\(\overrightarrow{r}\)=(x,y,z)に対する
1階の時間微分を表す速度ベクトル\({\overrightarrow{v}=\Large\frac{d\overrightarrow{r}}{dt}}\)=(vx,vy,vz)と、
2階の時間微分である加速度ベクトル\(\overrightarrow{a}=\Large{\frac{d^2\overrightarrow{r}}{dt^2}}\)=(ax,ay,az)について
基本ベクトルを球面座標系に変化した場合の成分はどうなるかを見てみます。
(その特別な場合として平面極座標への変換も分かります。)
vx=dx/dt,vy=dy/dt,vz=dz/dtおよび
ax=d2x/dt2,ay=d2y/dt2,az=d2z/dt2
r,θ,φの時間微分については2階微分のほうの式が少し複雑なので「ドット」で表すのがここでは便利です。ドットが2つ付いていたら2階での時間微分を意味します。
dr/dt=\(\dot{r}\), dθ/dt=\(\dot{\theta}\), dφ/dt=\(\dot{\varphi}\)
d2r/dt2=\(\ddot{r}\), d2θ/dt2=\(\ddot{\theta}\), d2φ/dt2=\(\ddot{\varphi}\)
の表記で式を整理します。
xとyについては積の微分公式を2回使う形で計算をします。
また、θやφをtの関数として考えているので
合成関数の微分公式も同時に使っていく事になります。
例えば sinθやcosφなどの項の時間微分は
(d/dt)sinθ=(dθ/dt)cosθ=\(\dot{\theta}\cos\theta\)
(d/dt)cosφ=-(dφ/dt)sinφ=\(-\dot{\varphi}\sin\varphi\) のようになります。
等速円運動の時のようにx=Rcos(ωt)などとする例ではr=Rは定数であり、θ=ωtの時間微分だけを考えれば良い事になります。(また、平面運動なのでφは式に含まれません。)
しかしここではr,θ,φがいずれもtの関数であるとして一般的な式の形を書きます。
| \(\overrightarrow{r}\)=(x,y,z) | d/dt |
| x=rsinφcosθ | \(\dot{r}\sin\varphi\cos\theta+\dot{\varphi}r\cos\varphi\cos\theta-\dot{\theta}r\sin\varphi\sin\theta\) |
| y=rsinφsinθ | \(\dot{r}\sin\varphi\sin\theta+\dot{\varphi}r\cos\varphi\sin\theta+\dot{\theta}r\sin\varphi\cos\theta\) |
| z=rcosφ | \(\dot{r}\cos\varphi-\dot{\varphi}r\sin\varphi\) |
次に、理論的には1階微分をさらに時間微分する形で2階微分を計算して変換の公式に当てはめれば良い事になりますが、その直接計算は実はかなり面倒です。
具体的な計算式は補足・参考用の資料として記事の最後に載せるとして、計算結果の式は次のようになります。
2階の時間微分を計算後、
加速度ベクトルに変更の公式を適用するとr,θ,φ成分は次のようになります。
$$a_r=\ddot{r}-\dot{\varphi}^2r-\dot{\theta}^2r\sin^2\varphi$$
$$a_{\theta}=2\dot{r}\dot{\theta}\sin\varphi+2r\dot{\varphi}\dot{\theta}\cos\varphi+r\ddot{\theta}\sin\varphi$$
$$a_{\varphi}=2\dot{r}\dot{\varphi}+r\ddot{\varphi}-r\dot{\theta}^2\sin\varphi\cos\varphi$$
また、θ成分に関しては次のようにも書けます。
$$a_{\theta}=\frac{1}{r\sin\varphi}\frac{d}{dt}\left(r^2\dot{\theta}\sin^2\varphi\right)$$
ここではxy平面の角度をθとしているので、
もしその角度をφとおくなら上式はθとφの文字を入れ替えた形になります。
上式でφ=π/2とおき、時間によるφの変化はないなら平面の極座標での変換を表します。
φ成分がなくなり、r成分とθ成分の式中でsinφ=1となるので式は比較的簡単になります。
球面座標系への加速度ベクトルの変換の式においてφ=π/2かつdφ/dt=0であれば
平面における極座標での加速度ベクトルの変換の式になります。
$$a_r=\ddot{r}-\dot{\theta}^2r$$
$$a_{\theta}=2\dot{r}\dot{\theta}+r\ddot{\theta}=\frac{1}{r}\frac{d}{dt}\left(r^2\dot{\theta}\right)$$
ここではxy平面の角度をθとしているので、
もしその角度をφとおくなら上式はθとφの文字を入れ替えた形になります。
これらの結果から、球面座標系での運動方程式を作る事ができます。
運動方程式は「力ベクトル=加速度ベクトルと質量の積」という形です。そこで、成分に分けた時に加速度ベクトルの成分として上記の式を使えばよいわけです。それらの成分とはx成分やy成分ではなく、r成分やθ成分であるわけです。
球面座標系で運動方程式はr成分、θ成分、φ成分ごとに次のように表されます。
加速度ベクトルに変更の公式を適用するとr,θ,φ成分は次のようになります。
$$F_r=m\left(\ddot{r}-\dot{\varphi}^2r-\dot{\theta}^2r\sin^2\varphi\right)\hspace{5pt}(=ma_r)$$
$$F_{\theta}=m\left(2\dot{r}\dot{\theta}\sin\varphi+2r\dot{\varphi}\dot{\theta}\cos\varphi+r\ddot{\theta}\sin\varphi\right)\hspace{5pt}(=ma_\theta)$$
$$F_{\varphi}=m\left(a_{\varphi}=2\dot{r}\dot{\varphi}+r\ddot{\varphi}-r\dot{\theta}^2\sin\varphi\cos\varphi\right)\hspace{5pt}(=ma_\theta)$$
平面の極座標においては次のようになります。
$$F_r=m\left(\ddot{r}-\dot{\theta}^2r\right)$$
$$F_{\theta}=m\left(2\dot{r}\dot{\theta}+r\ddot{\theta}\right)=\frac{m}{r}\frac{d}{dt}\left(r^2\dot{\theta}\right)$$
このように運動方程式を書く時には、
力ベクトルの成分も加速度ベクトル同様にr成分、θ成分、φ成分として表されます。
「力」は任意の方向にベクトルと同じ規則で分解できるので(実験で示されます)、
自由な方向での成分を考える事ができます。
これを見ると、一応そのように表せるといっても結構複雑です。直交曲線座標の中では比較的構造が単純で分かりやすい球面座標系であっても、加速度ベクトルや運動方程式をその座標系で考えるとなると直交座標系からの基本ベクトルと成分の変換はそれほど容易でない事が分かります。
平面上の極座標で見れば比較的形は簡単にはなりますが、直交座標での形と比べるとやはり複雑さは増しています。運動方程式の極座標系での成分表示は、回転を伴う運動の一部の解析では有効に機能します(例えば万有引力だけが働く物体の軌道を調べる時など)。
参考:球面座標に変換後の加速度ベクトルの成分計算
参考資料として、非常に地味ですが
速度ベクトルの加速度ベクトルの各成分を直接計算した場合の式を記します。
ここでの計算では、積の微分の規則から式全体は \(\ddot{r}\)の項や\(\dot{r}\dot{\theta}\)の項に分けて、変換の公式を適用までした値を1つずつ計算して最後に合計値を出します。それら自体は単なる微分と三角関数の計算問題なので、「確かに結果の式が直接計算でも得られる」という事を見るための参考用資料です。
| r 成分 | Ar= | CrxAx+CryAy+CrzAz | = Axsinφcosθ+Aysinφsinθ+Azcosφ |
| θ 成分 | Aθ= | CθxAx+CθyAy+CθzAz | =-Axsinθ+Aycosθ |
| φ 成分 | Aφ= | CφxAx+CφyAy+CφzAz | = Axcosφcosθ+Aycosφsinθ-Azsinφ |
| \(\overrightarrow{r}\)=(x,y,z) | d/dt(1階微分) |
| x=rsinφcosθ | \(\dot{r}\sin\varphi\cos\theta+\dot{\varphi}r\cos\varphi\cos\theta-\dot{\theta}r\sin\varphi\sin\theta\) |
| y=rsinφsinθ | \(\dot{r}\sin\varphi\sin\theta+\dot{\varphi}r\cos\varphi\sin\theta+\dot{\theta}r\sin\varphi\cos\theta\) |
| z=rcosφ | \(\dot{r}\cos\varphi-\dot{\varphi}r\sin\varphi\) |
具体的なr,θ,φ成分の計算
tによる2階導関数(2階微分)はr,θ,φ成分のいずれにも共通して使えます。
異なるのは変換公式における方向余弦になります。
この表は、例えば式中の\(\ddot{r}\)の項の係数は
2階微分を行った時点の変換前でxにおいては\(\ddot{r}\)sinφcosθであり、
r成分への変換用の方向余弦sinφcosθを乗じるとsin2φcos2θとなっている事を記しています。
yとzについても同様に計算し、例として\(\ddot{r}\)の項については合計すると係数の値は1になります。
sin2θ+cos2θ=1の関係などで三角関数の大部分は式から消えて、
プラスマイナスで打ち消して無くなる項も多くあるために
最終的な結果で残る項は比較的少なくなります。
| \(\ddot{r}\) | 変換前 | r成分 | θ成分 | φ成分 |
| x由来 | sinφcosθ | sin2φcos2θ | -sinφsinθcosθ | sinφcosφcos2θ |
| y由来 | sinφsinθ | sin2φsin2θ | sinφsinθcosθ | sinφcosφsin2θ |
| z由来 | cosφ | cos2φ | 0 | -sinφcosφ |
| 合計 | ・・・ | 1 | 0 | 0 |
| \(\dot{r}\dot{\theta}\) | 係数 | r成分 | θ成分 | φ成分 |
| x由来 | -2sinφsinθ | -2sin2φsinθcosθ | -2sinφsin2θ | -2sinφcosφ sinθcosθ |
| y由来 | 2sinφcosθ | 2sin2φsinθcosθ | 2sinφcos2θ | 2sinφcosφ sinθcosθ |
| z由来 | なし | なし | なし | なし |
| 合計 | ・・・ | 0 | 2sinφ | 0 |
| \(\dot{r}\dot{\varphi}\) | 変換前 | r成分 | θ成分 | φ成分 |
| x由来 | 2cosφcosθ | 2cosφsinφcos2θ | -2cosφcosθsinθ | 2cos2φcos2θ |
| y由来 | 2cosφsinθ | 2cosφsinφsin2θ | 2cosφcosθsinθ | 2cos2φsin2θ |
| z由来 | -2sinφ | -2cosφsinφ | 0 | 2sin2φ |
| 合計 | ・・・ | 0 | 0 | 2 |
| \(\ddot{\varphi}\) | 変換前 | r成分 | θ成分 | φ成分 |
| x由来 | rcosφcosθ | rsinφcosφcos2θ | -rcosφcosθsinθ | rcos2φcos2θ |
| y由来 | rcosφsinθ | rsinφcosφsin2θ | rcosφcosθsinθ | rcos2φsin2θ |
| z由来 | -rsinφ | -rsinφcosφ | 0 | rsin2φ |
| 合計 | ・・・ | 0 | 0 | r |
| \(\dot{\varphi}^2\) | 変換前 | r成分 | θ成分 | φ成分 |
| x由来 | -rsinφcosθ | -rsin2φcos2θ | rsinφcosθsinθ | -rcosφsinφcos2θ |
| y由来 | -rsinφsinθ | -sin2φsin2θ | -rsinφcosθsinθ | -rcosφsinφsin2θ |
| z由来 | rcosφ | -rcos2φ | 0 | rcosφsinφ |
| 合計 | ・・・ | -r | 0 | 0 |
| \(\ddot{\theta}\) | 変換前 | r成分 | θ成分 | φ成分 |
| x由来 | -rsinφsinθ | -rsin2φcosθsinφ | rsinφsin2θ | -rcosφsinφ cosθsinθ |
| y由来 | rsinφcosθ | rsin2φcosθsinφ | rsinφcos2θ | rcosφsinφ cosθsinθ |
| z由来 | なし | なし | なし | なし |
| 合計 | ・・・ | 0 | rsinφ | 0 |
| \(\dot{\theta}^2\) | 変換前 | r成分 | θ成分 | φ成分 |
| x由来 | -rsinφcosθ | -rsin2φcos2θ | rsinφcosθsinθ | -rcosφsinφ cos2θ |
| y由来 | -rsinφsinθ | -rsin2φsin2θ | -rsinφcosθsinθ | -rcosφsinφ sin2θ |
| z由来 | なし | なし | なし | なし |
| 合計 | ・・・ | -rsin2φ | 0 | -rcosφsinφ |
| \(\dot{\theta}\dot{\varphi}\) | 変換前 | r成分 | θ成分 | φ成分 |
| x由来 | -2rcosφsinθ | -2cosφsinφcosθsinθ | 2rcosφsin2θ | -2rcos2φ cosθsinθ |
| y由来 | 2rcosφcosθ | 2cosφsinφosθsinθ | 2rcosφcos2θ | 2rcos2φ cosθsinθ |
| z由来 | なし | なし | なし | なし |
| 合計 | ・・・ | 0 | 2rcosφ | 0 |
成分ごとに合計すると、加速度ベクトルの変換後の各成分は
\(a_r=\dot{r}-\dot{\varphi}^2r-\ddot{\theta}^2r\sin^2\varphi\)
\(a_{\theta}=2\dot{r}\dot{\theta}\sin\varphi+2\dot{\theta}\dot{\varphi}r\cos\varphi+\ddot{\theta}r\sin\varphi\)
\(a_{\varphi}=2\dot{r}\dot{\varphi}+\ddot{\varphi}r-\dot{\theta}^2r\cos\varphi\)
になります。
他の計算の仕方としては、変換の公式を先に使って例えばvr=vxsinφcosθ+vysinφsinθ+vzcosφの形で表して、その式の時間微分をするという方法もあります。その場合でも計算式は多少長くなります。
