三角形の合同 | 理数系学習サイト　kori

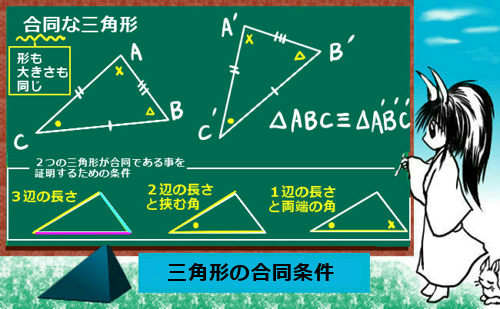
２つの三角形が合同であるとは、形も大きさも全く同じである事を言います。
形も大きさも同じという事は、面積も等しくなります。

合同な三角形であっても、向きなどが別々の方向を向いていて「見た目」が異なってる場合もあります。２つの三角形が合同であるかを調べるには次の３つの条件を満たしているかを調べます：

三角形の合同条件

次のいずれか１つを満たせば２つの三角形は合同です。

３辺の長さがそれぞれ等しい
２辺の長さとそのはさむ角の大きさが等しい
１辺の長さと両端の角の大きさがそれぞれ等しい

２つの三角形が合同である事は「３本線」の記号を使って△ＡＢＣ≡△ＤＥＦのように書きます。この時、角度が等しい頂点が対応するようにします。例えば△ＡＢＣ≡△ＤＥＦと書いている場合には∠ＢＣＡ＝∠ＥＦＤである事も表しています。

合同である三角形は、この３つの条件全てを満たします。つまり、１つの条件を満たせば他の２つの条件も同時に満たされるという事です。合同である事を証明するには１つの条件が満たされている事を示せば十分という事になります。

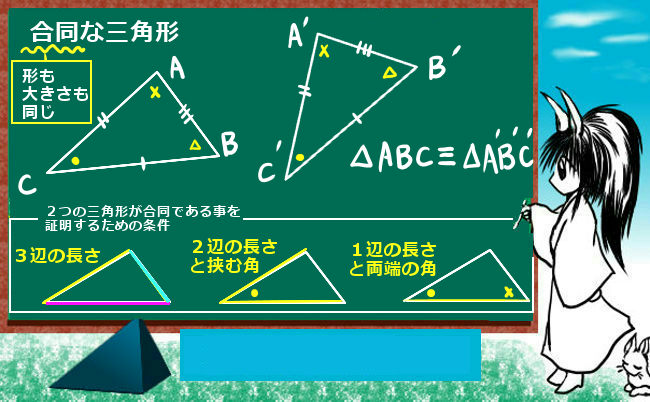
三角形の合同条件 — ２つの三角形が合同である事の証明においては例えば「２辺とそのはさむ角」の条件を使う場合には、①ＡＣ＝Ａ’Ｃ’　②ＢＣ＝Ｂ’Ｃ’　③∠ＡＣＢ＝∠Ａ’Ｃ’Ｂ’　の３つを明らかにする事で△ＡＢＣと△Ａ’Ｂ’Ｃ’ は合同である事を証明できます。

図を見ると分かりやすいと思うのですが、ある三角形に対して合同な別の三角形とは、１つの三角形を回転や反転させたものであると言う事もできます。イメージとしてそのように捉えるとよいでしょう。
回転や反転は角度や辺の長さを「不変」に保つ操作であるとも言えます。

合同の関係と似ているものとして、相似の関係があります。相似とは「形だけが同じで大きさは違う」というものです。

形も大きさも同じである場合が合同の関係であり、２つの三角形が合同である場合は相似である条件も満たしています。つまり、合同と相似は無関係なものではなくて、形も大きさも等しくなるためのやや厳しい条件が課されるのが合同で、形だけが等しい緩い条件だけが課されているのが相似というわけです。

一見すると合同にはみえないけれどよく見ると合同であるという例は、例えば三平方の定理の証明の１つで見られます。この例では形も大きさも全く同じ三角形が存在するのですが、向いている方向が全く異なるうえに他の様々な線が入り乱れているので気付きにくいのです。

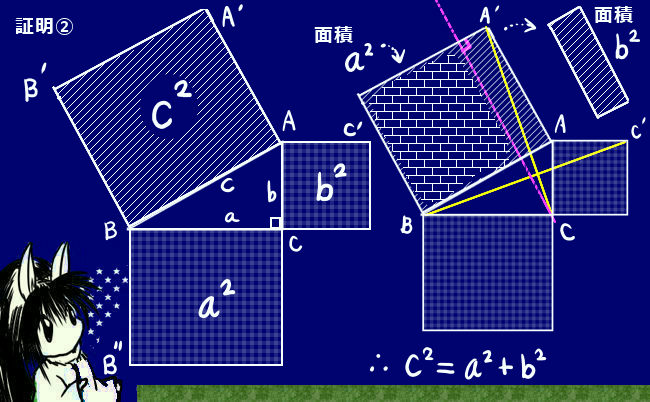
しかし、丁寧に辺の長さや角度を調べると確かに合同である事を示せます。この場合では「２辺とその挟む角が等しい」という条件を使っています。

図の３つの四角形は「正方形」であるという条件があるので、
ＡＣ＝ＡＣ’　ＡＢ＝ＡＢ’　という長さの関係がまずあります。
次に、∠ＢＡＣ＝∠ＣＡＢ＋∠ＣＡＣ’＝∠ＣＡＢ＋９０°ですが、
他方で∠Ｂ’ＡＣ’＝∠ＣＡＢ＋∠Ｂ’ＡＢ＝∠ＣＡＢ＋９０°なので
∠ＢＡＣ＝∠Ｂ’ＡＣ’になります。
ゆえに、△ＡＢＣ≡△ＡＢ’Ｃ’　である、と証明されます。

こういう具合に、合同である事を示すわけです。
尚、この例の場合では、「合同ゆえに面積も等しい」と話が続いていきます。

このように「見ただけでは分かりにくい」場合であっても、辺の長さや角度を調べて合同である事を確かに示せる場合があるわけです。数学的に論証するという事を学ぶ１つの意味がここにあります。単に論理的な思考をするというだけでなくて、事実関係の検証をする１つのツールとしての意味があるという事です。

３辺が全て等しいという条件を使う場合も、たまにあります。例えば、円に外接する三角形の頂点と円の中心で構成される２つの三角形です。

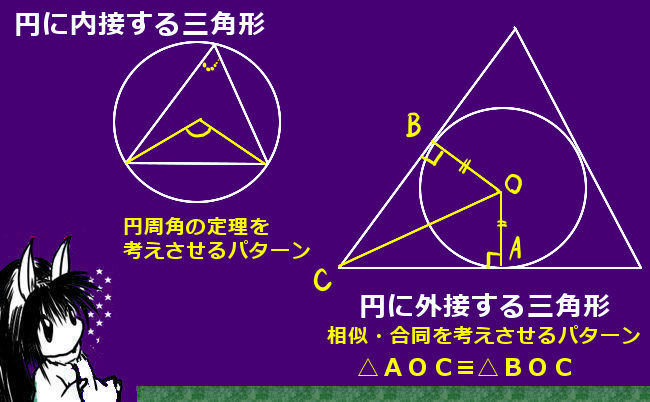
上図において、△ＡＯＣと△ＢＯＣに注目します。
まず、同じ円の半径なのでＯＡ＝ＯＢです。
また、辺ＯＣは共有されているのでもちろん長さは２つの三角形で等しいのです。
さらにここで、∠ＯＡＣ＝∠ＯＢＣ＝９０°なので、三平方の定理によりＡＣ＝ＢＣになります。
よって２つの三角形の３つの辺の長さはそれぞれ等しく、確かに△ＡＯＣ≡△ＢＯＣというわけです。

☆この場合について細かい事を言うと、∠ＯＡＣ＝∠ＯＢＣであっても、９０°でなければ、この部分の角の大きさが等しいというだけで合同とは言えないのです。
これは、式で示すのであれば余弦定理を使います。すると、９０°以外でこの部分の角の大きさが等しい場合には、ＡＣの長さとして「２つ」の解が得られる事があります。つまり、合同である場合とそうでない場合が生じ得るのです。
そのため、２辺の長さと「どれでもいいから１つの角」が等しいというだけでは、それだけで必ず合同であるとは断定できないのです。他方、その角度が９０°であれば余弦定理において解は１つだけなので合同であると言えます。もちろん、直角三角形において余弦定理は三平方の定理そのものです。
詳しく言うと、「２つの三角形が合同である」⇒『２辺の長さとどれか１つの角が互いに等しい』
という関係式は正しいのですが、その逆は言えないという事です。『２辺の長さとどれか１つの角が互いに等しい』という事は、２つの三角形が合同である事の必要条件ではあるけれども十分条件ではない、という事です。（この考え方は中学校では必要ありません。）

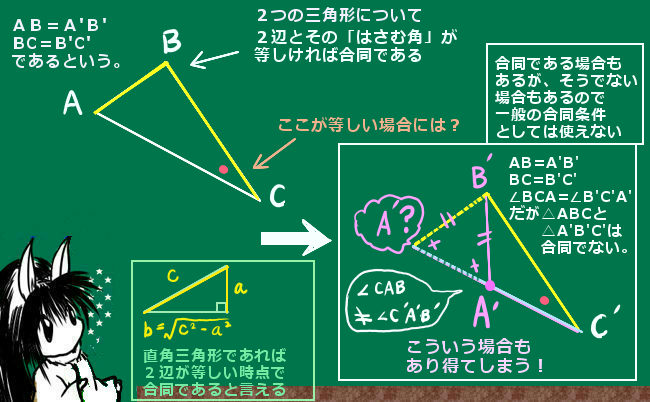
合同条件に関する注意点 — ２辺とその「はさむ角」がそれぞれ等しい場合に２つの三角形は合同になりますが、２辺が「はさんでいるわけではない」角度が等しい場合はどうなるのかを図で説明しています。

逆に、見た感じ同じ形・大きさに見えるけれどもきちんと調べるとじつは合同ではないというパターンもあり得ます。描かれた図ではいかにもそれらしく見えるけれども、条件を整理すると合同の３条件のいずれにも当てはまらず「じつは形も大きさも違う」という事が判明する場合もあります。

ここでは、あくまで図形問題に限定してという話ではありますが、「見た目」で判断するのではなく論拠を備えて検証するという事が三角形の合同条件や相似条件の学習において重要なポイントの１つです。これは試験問題を解くという話の中でも重要なので、おさえておきたいところです。