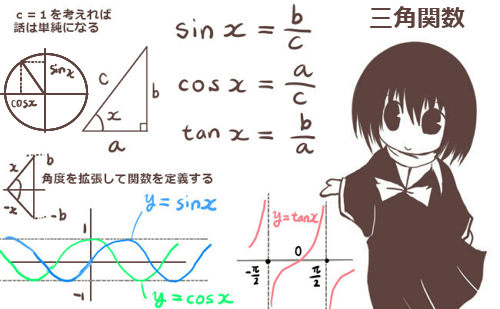
三角関数とは、図形上の三角比である正弦、余弦、正接の角度部分を拡張して定義域を実数全体に広げた正弦関数、余弦関数、正接関数を言います。(正接関数は \(\pi\)/2の奇数倍を定義域から除きます。 )
三角関数の変数は「実数値」であり、度数法ではなく弧度法で表します。(※度数法のまま三角関数を扱っても支障はない場合も多くあります。ただし微積分を扱う時には特に問題が発生するので注意も必要です。)
表記方法自体は三角比の場合と同じで、変数部分の記号としてxを使う事が多いです。
正弦関数 y=sinx 余弦関数 y=cosx 正接関数 y=tanx
三角関数は、代表的な周期関数の1つでもあります。これは、同じ関数の値が等間隔の変数ごとに繰り返し現れるというもので、「1回転」\(2\pi\) ごとの周期性を示します。(比例係数を使う事で、その他の値の周期とする事もできます。)
指数関数や対数関数と同じく、高校で扱われる重要な関数である初等関数の1つです。
三角比との違いは、数学的に厳密な違いが定義されているわけではありませんが、三角比というのはどちらかというと平面の図形に対して0°~180°の範囲で適用するものであって、三角関数は図形問題というよりは周期関数としての性質を強調して使う事が多いです。
定義域の拡張・・角度を拡張する
三角関数の考え方は大体において三角比と同じ考え方を適用できますが、正弦関数等の変数は実数全体です。この場合、単純な直角三角形の角度としては変になる場合はどのように解釈するのか?を説明します。
基本となるのは正弦関数と余弦関数なので、まずはそれらについて見ていきます。
(正接関数についてはそれらの割り算で表されます。)
■ 「0度」と負の角度 ■ \(\pi\)/2【90°】以上の角度 ■ 2\(\pi\)【360°】以上の角度【周期性】
「0度」と負の角度
直角三角形の直角以外の部分の角度は、「もちろん0°より大きく90°より小さい範囲」です。
弧度法だと 0 < x < \(\pi\)/2です。そうでないと三角形ができないためです。
しかし三角関数では、この変数の範囲(定義域)を拡張していきます。
まず変数が0以下の場合はどうするのでしょうか?結論を言うと次のようにします。
- sin 0 = 0, sin(-x)=-sinx と定義する。
- cos 0 = 1, cos(-x)= cosx と定義する。
- tan 0 = 0, tan(-x)=-tanx となる。【tanx=(sinx)/(cosx)と定義するため。】
ここでx>0であれば-xは負の値で、x<0であれば-xは正の値です。
後述しますがどちらの場合でも統一的にこれらの関係式を適用できます。
これは図で言うと、三角形を底辺に関して対照的にひっくり返したものを考えて「負の角度」としています。角度の方向にも向きを付けて、反時計回りをプラス、時計回りにはマイナスの符号をつけるという意味です。
そのうえで正弦については「下向き」の高さ、余弦については変わらず同じ値と決めています。

まずx=0の場合には次のようにしていす。
x=0とした時の y=sin x と y=cosx の値の定義です。
- 正弦関数の場合:sin 0 =0 と定義する。
- 余弦関数の場合:cos 0 =1 と定義する。
これらは「定義」であるとしか言いようがない面もありますが、「なめらかな形の連続関数」になるような定義としての1つの要請であるとも言えるのです。
三角比の範囲においても、角度を0に近づけると正弦の値は0に近づき、余弦の値は1に近づいていくのでx=0において sin 0 = 0, cos 0 = 1 であれば、その「点」において関数は「連続」になるという事です。さらにそこから、なめらかな形で負の部分に続いていく事も考えます。(微分可能になるように。)
また、周期関数になるという要請も加えると、定義の仕方も段々と限定されてくるわけです。意味としては、三角関数における「角度」の拡張の定義にはそのような意味があると捉える事ができるのです。
直交座標上にxを変数とした三角関数のグラフを描くと、ちょうどx=0で正弦関数は原点に対して点対称、余弦関数はy軸に関して軸対称の形になります。
ここでは表記としてはxがプラス符号であるとして、それにマイナスをつけた「-x」を負の数として扱っています。
- 正弦関数の場合:sin(-x)= -sinx【0から始まり-1に向けて関数の値は減少していく】
- 余弦関数の場合:cos(-x)= cosx【1から始まり0に向けて関数の値は減少していく】
$$例えば\hspace{10pt}\sin\left(-\frac{\pi}{4}\right)=-\sin\frac{\pi}{4}=-\frac{1}{\sqrt{2}},\hspace{10pt}\cos\left(-\frac{\pi}{4}\right)=\cos\frac{\pi}{4}=\frac{1}{\sqrt{2}}$$
正弦の場合と余弦の場合ともに、符号の関係にだけ注意すればよいという事になります。
値の絶対値については変数がプラスの場合のものをそのまま流用するという定義であるからです。
正弦の場合「0から減少していく」、余弦の場合「(最大値)1から減少していく」事を考えると理解はしやすいと思います。
尚、ここでは sin(-x)= -sinx において「xは正の値」を考えて変数が負の場合の説明をしましたが、
そこでx自体に「負の値」・・例えば-\(\pi\)/4を入れたとすると$$\sin\left\{-\left(-\frac{\pi}{4}\right)\right\}=\sin\frac{\pi}{4}=-\left(-\sin\frac{\pi}{4}\right)=-\sin\left(-\frac{\pi}{4}\right)$$となり、式の整合性はとれています。余弦関数の場合も同様に整合性がとれます。つまり一般的に、変数部分にマイナス符号がついている時には、上記の定義式の関係を使って機械的に計算してもよいという事です。
\(\pi\)/2【90°】以上の角度
では、変数がプラスの値の時に戻って、変数が\(\pi\)/2以上の場合はどうするのでしょう?
通常の図形問題でも90°以上の角度は考えますが、直角三角形の直角にはそのままでは適用できません。
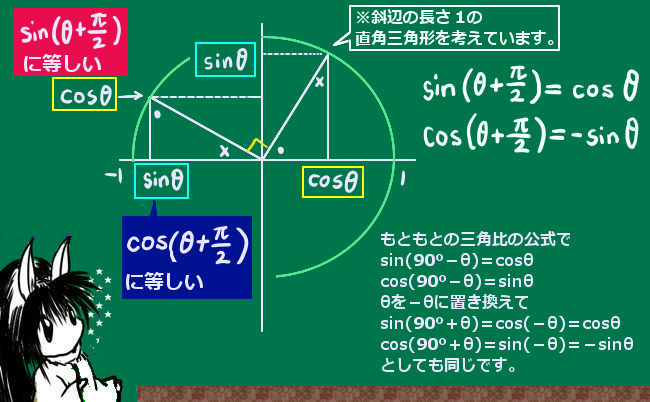
三角関数において、定義域を\(\pi\)/2以上に拡張する場合は次のようにします。
- sin(\(\pi\)/2) = 1, sin(x+\(\pi\)/2)=cosx と定義する。
【sin\(\pi\)=0, sin(3\(\pi\)/2)=-1, sin 2\(\pi\)=0 になる。】 - cos(\(\pi\)/2) = 0, cos(x+\(\pi\)/2)=-sinx と定義する。
【cos\(\pi\)=-1, cos(3\(\pi\)/2)=0, cos 2\(\pi\)=1 になる。】 - tan \(\pi\) = 0, tan(x+\(\pi\)/2)=-1/(tanx) となる。
【tanx=(sinx)/(cosx)と定義するため。】mを整数として tan(\(\pi\)/2+m)は、定義しない!【無限大を避けるためです。】
ここで正弦と余弦についてはxは実数のうち何の値でもよく、負の数や直角を超える値を入れたとしても整合性がとれた定義式になっています。
正接のほうについては、余弦関数の値がゼロになる変数の値は全て「穴」になるような形で定義域から除外する形で考えるという事です。ですから例えば tan(x+\(\pi\)/2)=-1/(tanx) においてはxの値として\(\pi\)の整数倍の時は除外する、という具合に考えます。
また、正弦関数と余弦関数については次式も成立し、これを使うと計算上便利です。
- sin(x+\(\pi\))=-sinx, sin(\(\pi\)-x)=sinx
- cos(x+\(\pi\))= -cosx, cos(\(\pi\)-x)=-cosx
これらは式としては統一的にまとめる事もできますが、図形的な意味としては別々に捉える事も1つの方法として便利である場合があります。正接関数についても同様の式を作る事は可能です。
さて、この定義を見ると角度が負の場合と比較して、かなり複雑であるようにも見えます。
この場合もやはり式だけで考えるのではなく、図形的に考えたものを式で表現するなら上記のようになると理解すべきでしょう。
変数が直角を考える場合には、今度は直角三角形の高さ部分の辺に関して対照的になるようにひっくり返すのです。この場合も、関数の値の絶対値は直角未満の場合の三角比の値を流用して符号だけをいじるという定義の仕方をします。
90°を超えて180°未満の「鈍角」の範囲における三角関数の具体的な値を調べる時には、鈍角を「180°-鋭角」と考えるか、「90°+鋭角」と考えるかの2通りの計算で便利なほうを使うのが普通です。
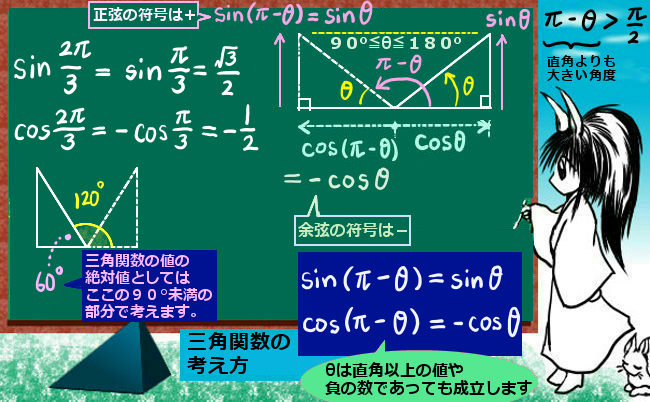
尚、式として考える場合、「90°+鋭角」の鋭角部分をマイナスにしてさらに90°加算する事で
「180°-鋭角」の三角関数の値の式を導出する事も一応可能です。次のようにします。
$$\sin\left(\pi-\theta\right)=\sin\left(\frac{\pi}{2}+\frac{\pi}{2}-\theta\right)=\cos\left(\frac{\pi}{2}-\theta\right)=-\sin(-\theta)=\sin\theta$$
$$\cos\left(\pi-\theta\right)=\cos\left(\frac{\pi}{2}+\frac{\pi}{2}-\theta\right)=-\sin\left(\frac{\pi}{2}-\theta\right)=-\cos(-\theta)=-\cos\theta$$
変数の値が2直角、つまり\(\pi\)の時には正弦関数の値は0、余弦関数の値は-1です。これは定義として捉えてもよいですし、上記の sin(x+\(\pi\))=-sinxから導出するという形でも同じです。これらも、意味としては関数の増減との対応・周期性・なめらかな連続性を満たす要件として考える事ができます。
さらに変数が\(\pi\)を超える場合には負の角度の時のように底辺に関して対照的にひっくり返します。この場合は、sin(x+\(\pi\))=-sinx, cos(x+\(\pi\))= -cosx の関係式を使うと把握しやすいでしょう。図を見ながら、図形的に捉えましょう。
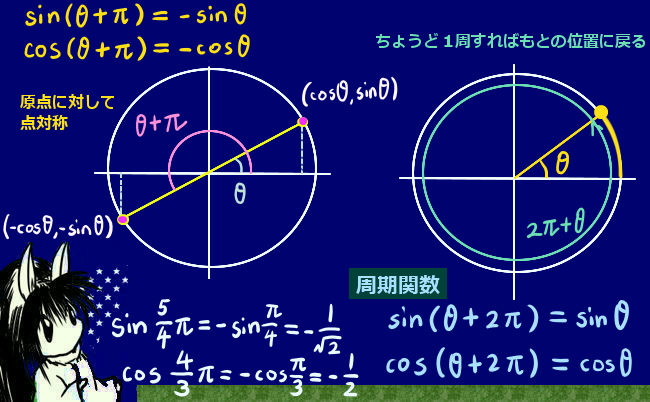
さらに角度の値を大きくすると、今度は再び高さ部分に関してひっくり返り、座標軸上で言うと第4象限の位置に配置された三角形を考える事になります。
2\(\pi\)【360°】以上の角度【周期性】
角度を増やして、4直角、つまり360°に達し、それを超えた場合はどうなるでしょう。
この場合は、sin(x+\(\pi\))=-sinx, cos(x+\(\pi\))= -cosx の関係式の変数にもう一度 \(\pi\) を加えるのです。
すると、再度符号が反転して sin(x+2\(\pi\))=sinx, cos(x+\(\pi\))= cosx となり、
もとの sinx および cosxになる事を導出できます。
これが三角関数の周期性と呼ばれる性質で、以降、角度をどれだけ増やしても延々と周期的に値を繰り返すという事です。これは正接関数についても成立します。
- sin(x+2\(\pi\))= sinx
- cos(x+2\(\pi\))= cosx
- tan(x+2\(\pi\))= tanx
この周期性は、マイナスの向きに角度を減らした場合にも適用できます。つまりマイナス方向にもプラス方向にも、実数全体にわたって2\(\pi\)の周期性があるという事です。
sin(x+2\(\pi\))=sinxの関係から、sin(2\(\pi\)-x)=sin(-x) となり、余弦関数の場合も同様です。これは図形的に見ると、同一の頂点に相当する部分に至る角度を反時計回り(プラス)で測っても時計回り(マイナス)で測っても三角関数の値は同じである事を意味します。
尚、sin2xのような関数を考える場合には、周期性は sin(2x+2\(\pi\))=sin2xのようになります。
するとこの場合には、xに着目するとsin(2x+2\(\pi\))=sin2(x+\(\pi\))のようになりますから、xの変化としては周期は\(\pi\)ごとに発生する事になるのです。xは\(\pi\)だけ変化すれば三角関数の変数全体では2\(\pi\)の変化になるので、それだけで周期が1サイクルしてしまうという事です。
グラフ上では通常の正弦関数よりも「密」になった波の形になります。
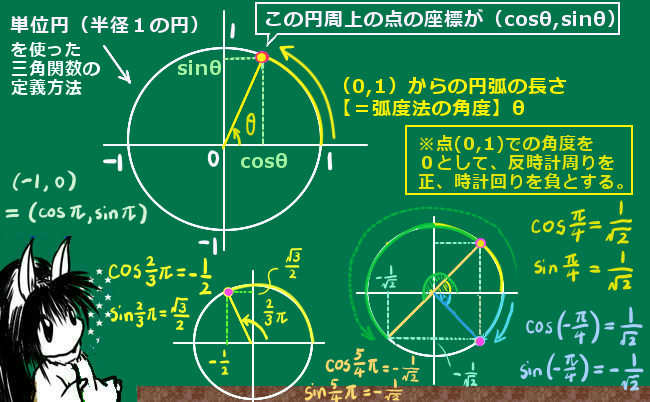
単位円による定義方法
さて、以上の三角関数の定義と性質を見ると、式だけで覚えるのは大変複雑で、図形的に見るとそれほど難しい理屈ではない事が分かると思います。
上記の図でもところどころに描いていますが、じつは三角関数を把握するには円を描くと便利です。(三角関数の別名を「円関数」とも言います。)
この円は、原点を中心とした半径を1にした円で、単位円と呼ばれます。
すると、斜辺の長さに相当する「半径」が1ですから、角度の取り方は前述の方法と同じであるとすると、
円周上の点のx座標は余弦関数の値、y座標は正弦関数の値になるのです。
この単位円による方法でも適切に三角関数の値を出せるので、これを定義にしてしまうやり方もあります。
直交座標上の原点を中心とする半径1の円周上の点(X,Y)を考えて、
(1,0)から測った円周の長さ(弧度法の角度に等しい)をxとします。この時、
- X=cosx すなわち余弦関数と定義する
- Y=sinx すなわち正弦関数と定義する
- 正接関数は tanx=(sinx)/(cosx) で定義する
各三角関数には2\(\pi\)の周期性があり、
角度は反時計回りをプラス符号、時計回りをマイナス符号として区別するものとします。
単純な覚えやすさと使いやすさに関しては、この単位円による方法は非常に優れています。
欠点があるとすれば、三角比の拡張として唐突に「円」を持ち出すと、やはり少しばかり飛躍を感じさせるのも事実だと思います。最初から単位円による定義で教え込まれてしまうと結局「わけもわからずに」暗記するだけ・・という事になりがちです。
重要な公式まとめ
三角関数の公式としては、簡単に4つのグループに分けると次のようなものがあります。
- 三角比についても適用できる公式
- 定義域を拡張した三角関数に特有なもの(例えば周期性)
- 正弦定理と余弦定理
- 加法定理と、それから派生する公式
まず、三角比についても成立するいくつかの公式は、三角関数でも成立します。これは三角比範囲の角度でのみ成立するのではなく、負の角度や直角以上の角度を代入してもきちんと成立するところが便利です。
次式は三角比について成立しますが、
定義域を実数全体とする三角関数においても成立します。
$$\tan x=\frac{\sin x}{\cos x}$$
$$\cos^2 x+\sin^2 x=1$$
$$\cos \left(\frac{\pi}{2}- x\right)=\sin x$$
$$\sin \left(\frac{\pi}{2}- x\right)=\cos x$$
$$\tan \left(\frac{\pi}{2}- x\right)=\frac{1}{\tan x}$$
角度についてはここでは弧度法で記しましたが、単純な図形問題にこれらを適用する際には角度を度数法で記しても大きな問題は普通は起きません。
これらの証明は三角比の説明のところで詳しく記しています。
周期性も含めて、三角関数特有の公式・性質も整理しておきましょう。
前述の通り、式だけで覚えるのではなく図形的に理解して覚えるとよいと思います。
これらは特に三角関数において成立する関係式です。
$$\cos \left(\frac{\pi}{2}+ x\right)=-\sin x$$
$$\sin \left(\frac{\pi}{2}+ x\right)=\cos x$$
$$\sin(-x)=-\sin x\hspace{20pt}\cos(-x)=\cos x$$
$$\sin(\pi +x)=-\sin x\hspace{20pt}\cos(\pi +x)=-\cos x$$
$$\sin(\pi -x)=\sin x\hspace{20pt}\cos(\pi -x)=-\cos x$$
$$\sin(2\pi +x)=\sin x\hspace{20pt}\cos(2\pi +x)=\cos x$$
最後の関係式については周期性と呼ばれる事は前述した通りです。
正接関数については、全てtanx=(sinx)/(cosx) の関係から公式を作る事ができます。
図形的に三角形に対して成立する公式で三角関数を使うものには、正弦定理と余弦定理というものがあります。(余弦定理のほうがどちらかというと重要かと思います。)それらは基本的には三角比に対して成立しますが、角度として鈍角や直角を適用する場合には三角関数の定義を使用すると図形的な対応もうまくとれるという具合になります。図形的な対応さえきちんとつけるなら、余弦定理に関しては全実数の範囲の角度を適用しても成立します。
- 正弦定理:三角形の辺a、b、cの対角の大きさをそれぞれA,B、C、三角形に外接する円の半径をRとすると
a/sinA=b/sinB=c/sinC=2R - 余弦定理:三角形の辺a、b、cと、辺aの対角の大きさAについて次の関係が成立する。
a2=b2+c2-2bccosA
【特にAが直角の時は三平方の定理そのもの】
また、三角関数の加法定理というものがあって、これは複素数の理論の一部を構成しており、微積分のほうで計算を進めるために使う事もあるので三角関数の公式の中では重要な部類に入ります。
また、この加法定理から派生するいくつかの小さなグループの公式として積和の公式・和積の公式・倍角の公式と呼ばれるものもあります。それらは本質的にはもともと加法定理そのもので、少し式変形をして形を変えたものになります。
2つの角度の大きさ A, B に関して次式が成立します。
- sin(A+B)=sinAcosB+cosAsinB
- sin(A-B)=sinAcosB-cosAsinB
- cos(A+B)=cosAcosB-sinAsinB
- cos(A-B)=cosAcosB+sinAsinB
正接関数についても、tan(A+B)=sin(A+B)/cos(A+B) の計算によって加法定理の公式を作る事が可能です。
この他に、高校数学では必要ありませんが、三角関数を使った無限級数によって周期関数を解析する技法があります。そこでも三角関数の基本的な性質や公式は前提として話が進められる事も多いので、基礎事項をよく知っておくと後々の学習が進めやすい事もあろうかと思います。