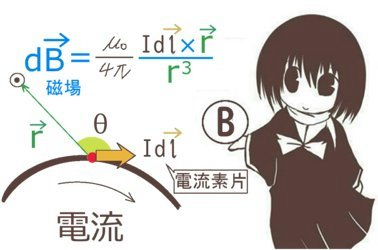
ビオ・サバールの法則【電流素片が作る磁場の式】

ビオ・サバールの法則とは電流が作る磁場の大きさと向きを表す法則です。
電流が作る磁場を表現する法則としてはアンペールの法則もありますが、特定の条件下でビオ・サバールの法則とアンペールの法則は等価である法則となります。

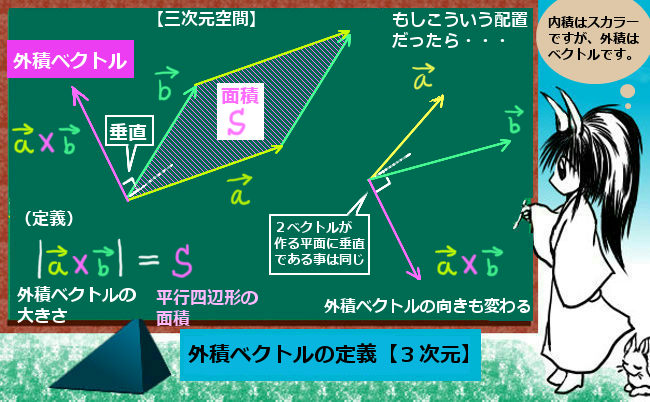
数式的には外積ベクトル（ベクトル積）を使って表現されるものであり、向きも含めて電流の向きと発生する磁場の関係が表現されます。（電流・磁場・力の関係を表す「ローレンツの力」も同様に外積ベクトルを使って表現されます。そしてその事は、ビオ・サバールの法則と無関係では無いという物理学的な見方があります。）

電磁気学での位置付け

ビオ・サバールの法則は磁場に関する法則ですが、電場で言えばクーロンの法則に対応する法則です。

磁場についてもクーロンの法則というのは実はあるのですが（後述します）、磁場に関する法則としてはビオ・サバールの法則が基本的な法則であると考えられる事が多いです。

しかしビオ・サバールの法則は、クーロンの法則（電場、磁場に関して共に）と比較すると式の形が複雑でなかなか計算もしづらいともよく言われます。実際、数式としての表され方も外積ベクトルを含む形になっており、他の電磁気学の諸法則と比べると直接的には少し扱いにくい面はあると言えます。
しかしビオ・サバールの法則には、直線電流に限らず「任意の形状」の電流が作る回路による磁場を向きも含めて表現するという意味合いががあります。

それに対して、アンペールの法則も磁場に関する法則ですが「磁場の回転（および閉曲線上での接線線積分）と電流の関係」を表す式になります。ビオ・サバールの法則そのものには回転の情報は入っておらず。むしろ「ベクトルとしての磁場を電流を使って直接計算する形」をしています。また、磁場に関するガウスの法則もやはり磁場についての法則ですが、そちらは磁場の「発散（div）」に関する法則です。

ビオ・サバールの法則は物理学での「法則」ですので、本質的にはそれを１つの「事実」と考えて必要に応じて使えばよいという性質のものです。
ただし、この法則は単独で実験データのみから得られる式であるというよりは、別の実験事実や理論を数式的に整理して改めて１つの法則と考える見方もできます。

そこで、この記事の後半ではビオ・サバールの法則を「導出」する２つの考え方も紹介します。そこではローレンツ力、磁場に関するクーロンの法則、ベクトルポテンシャル（間接的にアンペールの法則とガウスの法則）とビオ・サバールの法則との関係を物理学的な見方も含めて数式で説明します。

ビオ・サバールの法則の式

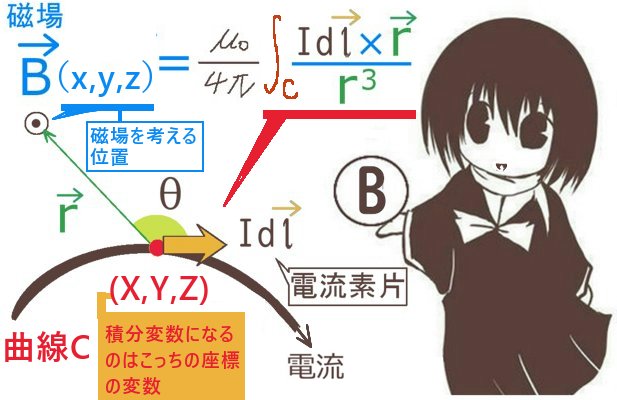
ビオ・サバールの法則とは数式としては次のように電流とそれによって作られる磁場（基本的には静磁場）の定量的な関係を、外積ベクトルを使って表現したものです。

電流素片\(Id\overrightarrow{l}\)の事は「電流要素」と呼ぶ事もあります。

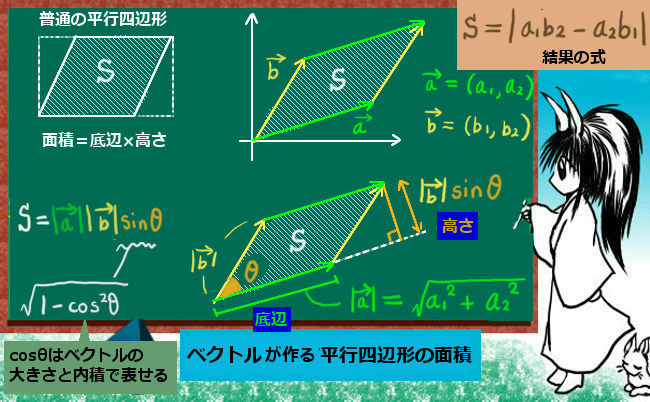
ビオ・サバールの法則には見かけ上分母に距離の３乗が入っていますが、１つは位置ベクトルを「方向だけを表す単位ベクトル」として表すために付けているだけなので本質はｒの「２乗」です。もしベクトルの大きさ（「強度」とも言う）だけに着目するなら、電流素片のベクトルと位置ベクトルのなす角をΘとして次の形になります。

$$\left| \frac{\overrightarrow{r}}{r}\right|=1\hspace{5pt}に注意して、\hspace{5pt}\left|d\overrightarrow{l}\times \frac{\overrightarrow{r}}{r}\right|=dl\sin\theta\hspace{5pt}であるから$$

$$dB=\frac{\mu_0}{4\pi}\frac{Idl\sin\theta}{r^2}=\frac{\mu_0}{4\pi}\frac{j\sin\theta dv}{r^2}$$

また、後述する事にも関係しますがビオ・サバールの法則の係数μ_０／(４π)は磁場に関するクーロンの法則の比例定数や、静磁場のベクトルポテンシャルを積分で表した式における係数と同じものになっています。

実際にこの法則を使って具体的な計算をする時には基本的に積分の形にします。
電流素片を集めて積分にする場合には
「曲線状の積分路に対して外積を微小量とした積分（内積ではなく）」を考えて、
電流密度を使った式の場合には体積積分を考えます。

いずれの場合も、ビオ・サバールの法則の基本の形に積分を付けて考えればよいのですが積分変数が何であるかには注意する必要もあります。磁場を考える座標は基本的には「積分の中では定数扱い」です。積分変数として考えるのは、積分の経路となる導線等における接線ベクトル（あるいはその始点の座標）を区別する必要があります。

混乱しやすい点をあらかじめ整理しておくと次のようになります。

• 磁場に関しては「磁場を表すベクトル場」と、
  その始点となっている位置座標の２つを考えている。
• 電流が生じている導線等においても「電流素片のベクトル」（向きは導線の接線ベクトル）と、
  その始点となっている位置座標の２つを考えている。電流密度ベクトルを考えている場合も同じです。

変数の表記については\(\overrightarrow{B}(x,y,z)=\overrightarrow{B}\left(\overrightarrow{R_B}\right)\)のようにも書けます。

多少煩雑になりますが変数などをより明確にして書くなら次のようになります。

$$\overrightarrow{B}\left(\overrightarrow{R_B}\right)=\overrightarrow{B}(x,y,z)=
\frac{\mu_0I}{4\pi }\int_C
\frac{d\overrightarrow{l}\left(\overrightarrow{R_L}\right)\times \left(\overrightarrow{R_B}-\overrightarrow{R_B}\right)}
{\left|\overrightarrow{R_B}-\overrightarrow{R_L}\right|^3}$$

$$=\frac{\mu_0I}{4\pi }\int_C
\frac{d\overrightarrow{l}(X,Y,Z)\times \left(x-X,y-Y,z-Z\right)}
{\left(\sqrt{(x-X)^2+(y-Y)^2+(z-Z)^2}\right)^3}$$

（※ただし、もしこの形の積分を普通の定積分として具体的に計算するなら基本的に３変数としてではなく曲線Cの各位置に対応するパラメーターとしての１つの実変数が必要になります。）

電流密度を使った場合も、「敢えて書くと」次式です。
（積分の区間の端点についてはてきとうな文字で置いています。）

$$\overrightarrow{B}(x,y,z)=
\frac{\mu_0}{4\pi}\int_V
\frac{\overrightarrow{j}\left(\overrightarrow{R_L}\right)\times \left(\overrightarrow{R_B}-\overrightarrow{R_B}\right)dv}
{\left|\overrightarrow{R_B}-\overrightarrow{R_L}\right|^3}$$

$$=\frac{\mu_0}{4\pi}\int_a^b\int_c^d\int_u^w
\frac{\overrightarrow{j}(X,Y,Z)\times \left(x-X,y-Y,z-Z\right)}
{\left(\sqrt{(x-X)^2+(y-Y)^2+(z-Z)^2}\right)^3}dXdYdZ$$

しかし次に具体例で説明するように、なるべく簡単なモデルを考えて変数の撮り方も工夫する事によって積分は３変数ではなく１変数で計算できる事もあります。

具体的にビオ・サバールの法則で計算をする例

実際問題としてビオ・サバールの法則から積分で直接的に磁場のベクトルを計算する場合には、できるだけ分かりやすい図のモデルを用意して「方向」と「大きさ」も分けて考えて、角度を変数として考えれるように変数変換する事で（１変数の積分で）計算をするといった工夫をしたりします。

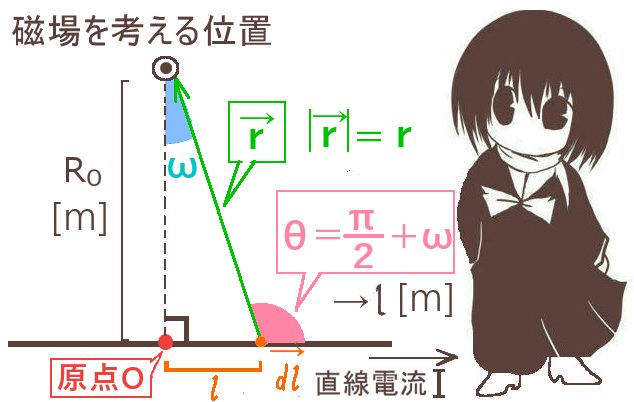
比較的簡単な例として、直線状の導線上における定常電流が導線の周囲に作る磁場をビオ・サバールの法則を使って計算してみます。積分する範囲も「曲線」ではなくて直線で考えて、さらに電流も当然それに沿った向きなので、積分に関してはベクトルではなくて１変数の積分区間として考えてしまうわけです。（図での位置関係に関してはベクトル的な関係も考慮する必要があります。）

積分をする前に、法則の基本となる形のほうで状況を整理します。電流の向きを画面上の左から右に向かう方向にとると、ビオ・サバールの法則が言うには磁場の方向は「電流素片のベクトル×導線から磁場の位置までのベクトル」という外積ベクトルの方向であるから、「画面奥から画面手前」の向きです。そこで、向きは確定したので次は大きさだけを見るという流れになるのです。

1. まず磁場の「向き」を確定させます。（ビオ・サバールの法則により外積ベクトルの向き。）
2. 次に、磁場の大きさだけを積分で計算します。

磁場を考える位置から導線に向かって垂線をおろして、その足（交点）を原点とします。そして、そこから磁場を考える位置までの距離をR_０とします。このR_０は定数です。

大きさだけに着目すると、平面幾何的な角度の関係に注意すると次の式が成立します。これは前述の、ベクトルの大きさだけに着目した場合のビオ・サバールの法則の式です。法則の外積ベクトルに由来する角度をΘとして、計算をしやすくするために補足的に考えた「原点・磁場を考える位置・電流素片（の始点）の位置」で作られる角度ωとしています。

$$dB=\frac{\mu_0}{4\pi}\frac{Idl\sin\theta}{r^2}=\frac{\mu_0I}{4\pi r^2}\sin\left(\omega+\frac{\pi}{2}\right) dl=\frac{\mu_0I}{4\pi r^2}\cos\omega\hspace{3pt} dl$$

途中計算には三角関数の公式を使用しています。

ここで、積分する時の変数は導線の長さを表す位置ですが、これは１変数として扱えます。しかし図の位置関係から、ωやｒは変数\(l\)に対して独立ではないので定数扱いはできない事になります。
この場合では、ωやｒを\(l\)に変換するよりも、統一してωの関数に変換して積分をするほうが簡単です。ただし、この変換をする時は最初から微小量で考えるのではなく、普通の関数として考えてから微分をする必要がありますので注意。

定積分を\(l\)＝aからbまで行うとして、対応するωをω₁ とω₂とします。

\(\left|\overrightarrow{B}\right|=B\) とすると、計算は次のようになります。

$$\cos\omega=\frac{R_0}{r}\Leftrightarrow \frac{1}{r}=\frac{\cos\omega}{R_0}\hspace{15pt}l=R_0\tan\omega\hspace{15pt}\frac{dl}{d\omega}=\frac{R_0}{\cos^2\omega}\hspace{3pt}であるので、$$

$$B=\int_a^bdB=\int_a^b\frac{\mu_0I}{4\pi r^2}\cos\omega dl=\frac{\mu_0I}{4\pi }\int_{\omega 1}^{\omega 2}\frac{\cos^2\omega}{R_0\hspace{1pt}^2}\cos\omega\frac{dl}{d\omega}d\omega$$

$$=\frac{\mu_0I}{4\pi }\int_{\omega 1}^{\omega 2}\frac{\cos^3\omega}{R_0\hspace{1pt}^2}\frac{R_0}{\cos^2\omega}d\omega=\frac{\mu_0I}{4\pi R_0}\int_{\omega 1}^{\omega 2}\cos\omega d\omega$$

$$=\frac{\mu_0I}{4\pi R_0}(\sin\omega_2 -\sin\omega_1)$$

使用した微分に関する公式等は次の２つです。

• 正接関数（tan x）の微分の公式
• 置換積分の公式

式が一見込み入るようですが丁寧に計算すると単独の余弦関数を積分すればよいだけになり、このように結果を出せるわけです。この結果でω_１→－π／２とω_２→π／２の極限を考えると、
「導線が無限に（十分に）長いとみなせる場合」の結果となり、またアンペールの法則から計算した結果にも一致するようになります。

このように、想定するモデルを工夫すると一見複雑であるビオ・サバールの法則の式の計算を、通常の１変数の定積分にまで簡略化できたりするわけです。こういった手法は電磁気学で（あるいは物理学全般で）使用され、物理現象の考察に活用されます。

法則の由来①：ローレンツ力や磁場に関するクーロンの法則等の組み合わせによる帰結と解釈する方法

電流と磁場の関係については次のような事実が実験によって知られています。

• 直線電流の周りには環状の磁場が作られる。（エールステッドによる実験）
• 電流が生じている２本の平行導線には互いに力が働く。
  ２つの導線の電流が同じ向きなら引力であり、
  向きが互いに逆なら力は斥力（反発する力）。（アンペールなどによる実験）
• 磁場の中で運動している電荷は力を受ける。（「ローレンツの力」）
• 磁気を帯びた物体同士には電気を帯びた物体同士同様の力が働く。
  （磁場に関するクーロンの法則）

直線電流が作る環状の磁場は、アンペールの法則から得られる結果の１つと捉える事が可能です。

これらの実験事実やその理論の組み合わせの帰結としてビオ・サバールの法則の式が得られるという物理学的な解釈の方法があります。ここではその導出過程を詳しく見ます。

電流が生じている平行な導線（以下、簡単のために「平行電流」と書きます）の相互に働く力は、２つの電流の大きさのそれぞれに比例し、導線の長さにも比例し、さらに平行電流間の距離ｄに反比例するというデータが得られていました。

平行電流に働く力は、電流による環状磁場とローレンツの力の組み合わせで生じるという見方ができます。さらに、そこに磁場に関するクーロンの法則を組み合わせて少し考察するとビオ・サバールの法則を積分したものと同じ形の式ができます。そしてそれがビオ・サバールの法則の電流素片による表記の由来となっていて、法則が成立する理論的な裏付けの１つであるという見方も可能であるわけです。

まず電荷密度ρがある速度で動いている時に、これを電流密度として解釈します。ローレンツの力は磁場中で導線自体が動いている時に働く力でもありますが、導線に沿って電荷が動いて流れになっている（すなわち電流が発生している）時にも同様に成立すると見るわけです。

$$\overrightarrow{j}=\rho\overrightarrow{v}$$

これを、単位体積（１ｍ^３）当たりで考えたローレンツの力の磁場だけの式に代入します。

$$\overrightarrow{F}=\rho\overrightarrow{v}\times\overrightarrow{B}=\overrightarrow{j}\times\overrightarrow{B}$$

これは１ｍ^３の式なので、Ｓ [ｍ^２]×ｄｌ[m]＝Ｓｄｌ[m^３]（これは外積ではなく普通の掛け算）の場合を書きます。ここではＳｄｌという量はスカラー扱いになりますから、特に順番も気にせずに単に乗じれば良い事になります。その場合の力を\(d\overrightarrow{F}\)とします。

$$d\overrightarrow{F}=\overrightarrow{j}\times\overrightarrow{B}Sdl=\left(S\overrightarrow{j}\right)\times\overrightarrow{B}dl$$

ここでの電流密度は「電荷密度×速度」で最初考えましたが、これを「電流ベクトル×面積」で表します。普通、電流はベクトルでは考えませんがここでは敢えて電流密度ベクトルに合わせたものを考えるという事です。

$$\overrightarrow{j}=\frac{\overrightarrow{I}}{S}\Leftrightarrow \overrightarrow{I}=S\overrightarrow{j}により、$$

$$d\overrightarrow{F}=\left(S\overrightarrow{j}\right)\times\overrightarrow{B}dl=\overrightarrow{I}\times\overrightarrow{B}dl$$

ここでｄｌはスカラーとしてきたわけですが「大きさはｄｌで方向は電流ベクトルに等しいベクトル」を改めて\(d\overrightarrow{l}\)とします。これを使うと「電流ベクトル」の向きはそのベクトルに含めてしまって、電流をスカラーとして扱えます。

$$d\overrightarrow{F}=\overrightarrow{I}\times\overrightarrow{B}dl=\left(dl\overrightarrow{I}\right)\times\overrightarrow{B}ですが、$$

$$dl\overrightarrow{I}=Id\overrightarrow{l}となるd\overrightarrow{l}を考える事ができるので$$

$$d\overrightarrow{F}=\left(dl\overrightarrow{I}\right)\times\overrightarrow{B}=Id\overrightarrow{l}\times\overrightarrow{B}$$

この式は、途中で考えていた「断面積S」が小さい値であるとすると一般的な導線における状況と解釈する事ができて、「電流素片が磁場から受ける力」と捉える事ができます。

次に、これを磁場に関するクーロンの法則と組み合わせます。

電流が生じている導線があって、曲線Cの形をしているとします。そこから離れた位置に磁気量ｑ[Wb] の磁気を帯びた小さな物体があるとして、近似的に点とみなせるとします。この物体は周囲に磁場を作り、大きさ等は磁場に関するクーロンの法則を使うとします。そこで物体から曲線C上のある電流素片の位置までのベクトルを\(\overrightarrow{R}\)とすると、電流素片が受ける力は次のように書けます。

$$d\overrightarrow{F}=Id\overrightarrow{l}\times\overrightarrow{B}=Id\overrightarrow{l}\times\frac{kq\overrightarrow{r}}{R^3}=kqI\frac{d\overrightarrow{l}\times\overrightarrow{R}}{R^3}$$

$$曲線C全体では、積分して\overrightarrow{F}=kqI\int_C\frac{d\overrightarrow{l}\times\overrightarrow{R}}{R^3}$$

形としてはかなりビオ・サバールの法則に近くなったように見えます。しかし、ここで考えている磁場は磁気を帯びた物体が作る磁場であって、電流が作る磁場ではないので注意。また、得られている式が表す量も「磁場によって電流素片が受ける力」です。磁場は、1[Wb] の磁気量を持つ試験磁荷（仮想的ですが）が他の物体由来の磁気から受けるです。

では次にどのように考えるのかというと、電流が磁場を発生させる事はエールステッドの実験や平行電流に関する考察から事実と受け取れるので、曲線C上の電流素片もまた周囲に磁場を作ると考えられます。さらにその磁場は、磁気を帯びた物体に力を及ぼすはずです。

ここで、数学ではなく物理的な見方になりますが力学の作用反作用の法則が、ここでも成立するはずだと見ると「電流素片がｑ[wb]の磁気量の物体に及ぼす力」は「ｑ[wb]の磁気量の物体が電流素片に及ぼす力」と大きさは同じで向きが逆の力ベクトル（数式ではマイナス符号が付く）になっていると予想できます。電流素片が作る磁場を\(\overrightarrow{B_I}\)とすると、磁気を帯びた物体が受ける力は\(q\overrightarrow{B_I}\)となります。そこで、これがさきほどの「ｑ[wb]の磁気量の物体が電流素片に及ぼす力」にマイナス符号を付けたものだとして式を作ると次式です。

$$q\overrightarrow{B_I}=-kqI\int_C\frac{d\overrightarrow{l}\times\overrightarrow{R}}{R^3}$$

$$\Leftrightarrow \overrightarrow{B_I}=-kI\int_C\frac{d\overrightarrow{l}\times\overrightarrow{R}}{R^3}$$

さらに、\(\overrightarrow{R}\)は「物体から電流素片」へのベクトルでしたから、「電流素片から物体」に向けてのベクトルとして\(\overrightarrow{r}=-\overrightarrow{R}\)に置き換えます。

$$ \overrightarrow{B_I}=-kI\int_C\frac{d\overrightarrow{l}\times\overrightarrow{R}}{R^3}=-kI\int_C\frac{d\overrightarrow{l}\times\left(-\overrightarrow{r}\right)}{r^3}=kI\int_C\frac{d\overrightarrow{l}\times\overrightarrow{r}}{r^3}$$

$$=k\int_C\frac{Id\overrightarrow{l}\times\overrightarrow{r}}{r^3}=\frac{\mu_0}{4\pi}\int_C\frac{Id\overrightarrow{l}\times\overrightarrow{r}}{r^3}$$

つまり、電流素片に関するビオ・サバールの法則を曲線Cに関して積分した式と全く同じものが得られました。この事から、もとのビオ・サバールの法則の式が成立する事の「理論的根拠」も得られたと捉える事もできるわけです。

この捉え方のもとでは、ビオ・サバールの法則の「距離の２乗に反比例」（ベクトル表記の時に書かれる３乗というのは形式上なので本質は２乗）という部分は磁場におけるクーロンの法則と同じ由来のものであり、外積の形になっている事はローレンツの力に由来すると考える事ができます。

法則の由来②：ベクトルポテンシャルから導出する方法

他方で、アンペールの法則のほうがまず成立していると考えて、静磁場のベクトルポテンシャルからビオ・サバールの法則の式を導出するという事もできます。電流密度を使ったほうのビオ・サバールの法則を積分で書いた式は、ベクトルポテンシャルを表す式に何となく形が似ています。そしてそれは偶然ではなくきちんと関係があると解釈できるという事です。

まず（静磁場の）ベクトルポテンシャルの式は次のような形です。

$$\overrightarrow{A}(x,y,z)=\frac{\mu_0}{4\pi}\int_V\frac{\overrightarrow{j}}
{r}dv$$

$$\left(\overrightarrow{R_B}=(x,y,z),\hspace{5pt}\overrightarrow{j}の各始点\overrightarrow{R_L}=(X,Y,Z)\hspace{3pt}のもとで\hspace{3pt}r=\left|\overrightarrow{r}\right| =\left|\overrightarrow{R_B}-\overrightarrow{R_L}\right|\right)$$

次に「ベクトルポテンシャルの回転が静磁場になる」ので、回転 rot を考えます。ただし、偏微分を行う対象はベクトルポテンシャルのほうですからここでの変数で言うと（ｘ，ｙ，ｚ）のほうです。積分変数として考えている（Ｘ，Ｙ，Ｚ）ではありません。
そこで、ここではその事を強調して回転の記号を rot_A と書いておきます。

$$\mathrm{rot}\overrightarrow{A}=\overrightarrow{B}であり、x,y,zでの偏微分を行う事を強調し回転を\mathrm{rot_A}と書くと$$

$$\overrightarrow{B}=\mathrm{rot_A}\overrightarrow{A}=\mathrm{rot_A}\left(\frac{\mu_0}{4\pi}\int_V\frac{\overrightarrow{j} }{r}dv\right)$$

$$\mathrm{rot_A}=\left( \frac{\partial A_3}{\partial y}-\frac{\partial A_2}{\partial z},\hspace{3pt}\frac{\partial A_1}{\partial z}-\frac{\partial A_3}{\partial x},\hspace{3pt}\frac{\partial A_2}{\partial x}-\frac{\partial A_1}{\partial y}\right)\hspace{10pt}dv=dXdYdZ$$

前述のように、回転における偏微分を行う変数は積分変数ではなく「ベクトルポテンシャルを考えている位置を表す３変数」です。
そこで、積分を考える範囲で電流密度の分布と関数形が連続的なものであれば、積分変数でない変数で「積分の中身」を微分しても結果に影響を与えません。（※数学の解析学的な補足説明は後述。）

$$\overrightarrow{B}=\mathrm{rot_A}\left(\frac{\mu_0}{4\pi}\int_V\frac{\overrightarrow{j} }{r}dv\right)=\frac{\mu_0}{4\pi}\int_V\mathrm{rot_A}\frac{\overrightarrow{j} }{r}dv$$

さてそこで、ベクトル解析における簡単な公式を２つほど使用して変形を行います。

さきほどの計算に戻ると、まず電流密度ベクトルは定ベクトルとみなせます（変数はX，Y，Zであり、これらはｘ，ｙ，ｚから見ると定数とみなせるので。）そして分母のｒについては計算上ｘ，ｙ，ｚに関するスカラー場と見なせますので１つ目の公式を適用できます。この時の外積の順序は電流密度ベクトルを先にしておきます。つまり公式で言うとマイナス符号が付いたほうを使います。

$$\mathrm{rot_A}\frac{\overrightarrow{j} }{r}dv=-\overrightarrow{j}\times\mathrm{grad}\frac{1}{r}$$

つまり、式の演算としては回転がなくなって外積に変わっているわけです。

ビオ・サバールの法則の式の形に近づいていますが、代わりに勾配 grad が入ってしまっています。
そこで\(\overrightarrow{r}=(x-X,y-Y,z-Z)\)において同じくX，Y，Zを定数とみなせば、公式を適用できて次式が成立します。

$$\mathrm{grad}\frac{1}{r}=-\frac{\overrightarrow{r}}{r^3}$$

これによって数式上、勾配もなくなります。
整理すると、磁場が電流密度を用いたビオ・サバールの法則を積分で書いた形で表せる事になります。

$$\overrightarrow{B}=\mathrm{rot_A}\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_V\mathrm{rot_A}\frac{\overrightarrow{j} }{r}dv$$

$$=\frac{\mu_0}{4\pi}\int_V- \overrightarrow{j}\times \mathrm{grad}\frac{1}{r}dv= \frac{\mu_0}{4\pi}\int_V- \overrightarrow{j}\times \left(-\frac{\overrightarrow{r}}{r^3}\right)dv$$

$$=\frac{\mu_0}{4\pi}\int_V \overrightarrow{j}\times \frac{\overrightarrow{r}}{r^3}dv= \frac{\mu_0}{4\pi}\int_V\frac{\overrightarrow{j}\times\overrightarrow{r}}{r^3}dv$$

この式で表される磁場はベクトルポテンシャルと同じくｘ，ｙ，ｚによるベクトル場です。
つまり\(\overrightarrow{B}=\overrightarrow{B}(x,y,z)\)です。

以上の事は、アンペールの法則（変位電流を含まない形）が成立する→静磁場のベクトルポテンシャルを放射ゲージ条件のもとで式で表せる→ビオ・サバールの法則を積分した形の式が成立するという流れです。そのため、ビオ・サバールの法則をアンペールの法則から導出するという見方とも言えます。
また、ベクトルポテンシャルを考えるうえでは磁場に関するガウスの法則も前提条件でしたから、上記の導出方法によれば磁場に関するガウスの法則も間接的に関わっていると言えます。