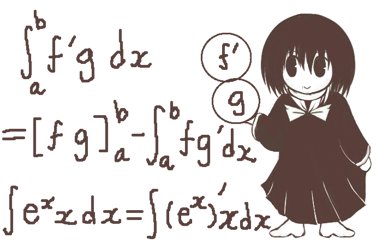部分積分の公式は「部分積分法」もしくは単に「部分積分」とも言い、置換積分と同じく積分において関数の原始関数(=微分するとその関数が得られる)を探すのに使われる基本公式の1つです。
英語名:integration by parts
公式の内容
関数が次の形をしている時には部分積分の公式を適用して積分の計算ができます。
この公式は不定積分でも定積分でもどちらでも使えて、
具体的な例に適用して計算していく場合はどちらの場合の形も使用します。
不定積分の場合は次式です。
$$\int \left(\frac{d}{dx}f(x)\right)g(x)dx=f(x)g(x)-\int f(x)\left(\frac{d}{dx}g(x)\right)dx$$
定積分の場合は次式になります。
$$\int_a^b \left(\frac{d}{dx}f(x)\right)g(x)dx=\large{[f(x)g(x)]}_a^b-\int_a^b f(x)\left(\frac{d}{dx}g(x)\right)dx$$
$$=f(b)g(b)-f(a)g(a)-\int_a^b f(x)\left(\frac{d}{dx}g(x)\right)dx$$
定積分のほうの形は、1つ前の段階として(d/dx){f(x)g(x)} に対する
積分区間 [a, b] での定積分を考えているのでこのような形の式になっています。
部分積分の公式を適用する事を指して「部分積分する」というふうにもよく言います。
文章の表現としては例えば「左辺を部分積分すると次のようになる」などといった具合に使います。
証明については次に述べますが、積の微分公式を変形したものを積分して公式が得られます。
また具体例についても後述しますが、部分積分の公式を実際の計算で適用する時には
まずてきとうなh(x)g(x)の形の関数に対する積分があって、
何か別の関数f(x)を考えると「h(x)=(d/dx)f(x)となるようだ」と気付く事で部分積分の公式を適用してみるといった流れになる事が多いと言えます。
$$計算で使う時は主に、\int h(x)g(x)dxの形の式に対して、$$
$$h(x)=\frac{d}{dx}f(x)となるようなf(x)を見つけて公式を適用します。$$
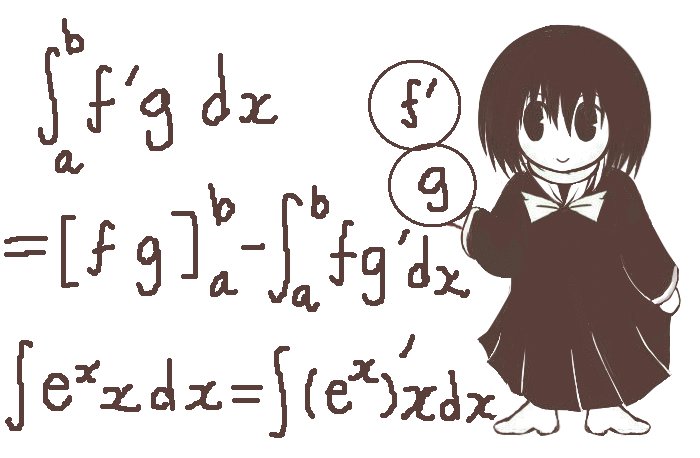
導出・証明
実は、部分積分の公式を導出する方法は微分の公式を知っていれば非常に簡単です。
置換積分法が合成関数の微分公式を根拠に成立しているのに対して、
部分積分法は積の微分公式を根拠に成立しています。
積の微分公式を書くと次のようになります。
$$\frac{d}{dx}(f(x)g(x))=\left(\frac{d}{dx}f(x)\right)g(x)+f(x)\left(\frac{d}{dx}g(x)\right)$$
微分の書き方が複数ある事などに由来して、例えば次のように書いても同じです。 $$\frac{d}{dx}(f(x)g(x))=\frac{df}{dx}g(x)+f(x)\frac{dg}{dx}$$ $$(f(x)g(x))^{\prime}=f^{\prime}(x)g(x)+f(x)g^{\prime}(x)$$ f(x)=f、g(x)=gと略記するなら次のようにも書けます。 $$(fg)^{\prime}=f^{\prime}g+fg^{\prime}$$
積の微分公式において、
右辺の片方の項(ここでは第2項)を左辺に移行します。
$$\left(\frac{d}{dx}f(x)g(x)\right)-f(x)\left(\frac{d}{dx}g(x)\right)=\frac{d}{dx}(f(x)g(x))$$
これを右辺=左辺の形に入れ換えます。
$$\frac{d}{dx}(f(x)g(x))=\left(\frac{d}{dx}f(x)g(x)\right)-f(x)\left(\frac{d}{dx}g(x)\right)$$
次に両辺をxに関して積分し、(d/dx){f(x)g(x)}のところは積分するとf(x)g(x)になります。
$$\int \left(\frac{d}{dx}f(x)\right)g(x)dx=\int\frac{d}{dx}(f(x)g(x))dx-\int f(x)\left(\frac{d}{dx}g(x)\right)dx$$
$$=f(x)g(x)-\int f(x)\left(\frac{d}{dx}g(x)\right)dx$$
すると、全体を見ると部分積分の公式になっています。(不定積分の項が残っているので任意定数はここではつけていません。)
ですので、積の微分公式を知っていれば非常に簡単な成り立ちの積分公式であると言えます。
定積分の場合も同じように部分積分の公式の内容を得られます。
不定積分の場合の最後から1つ前の式から考えると比較的分かりやすいかと思います。
$$\int_a^b \left(\frac{d}{dx}f(x)\right)g(x)dx=\int_a^b\frac{d}{dx}(f(x)g(x))dx-\int_a^b f(x)\left(\frac{d}{dx}g(x)\right)dx$$
$$=\large{[f(x)g(x)]}_a^b-\int_a^b f(x)\left(\frac{d}{dx}g(x)\right)dx$$
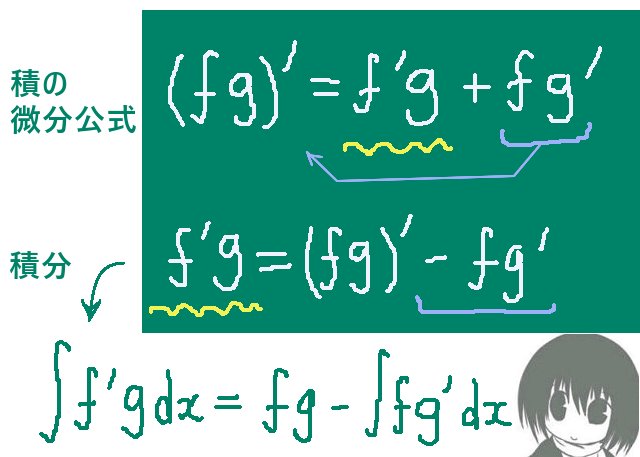
部分積分によって計算できる積分の例
初等関数の簡単な組み合わせであっても、
原始関数を直接探す事で積分を計算する事は一般的に非常に難しい事が知られています。
ですが、一部の関数については部分積分や置換積分によって原始関数が分かる場合があります。ここでは、部分積分の公式が使える代表的な例をいくつか挙げて説明します。
指数関数や三角関数との積になった関数
以下、指数関数と言ったら自然対数の底 e に対する exを考えるとします。
これは単独では(d/dx)ex=exなので積分も直接計算できますが、別の関数がくっついていると話が変わってきます。三角関数についても似た事が言えます。
例えば次のような関数です。
- xex
- x2ex
- xsinx
- exsinx
こういった形の関数の積分は、部分積分の公式を使う事によって原始関数が分かるようになり、それで積分を計算する事ができます。
1つ1つ具体的に見て行きますが、基本的な考え方は「積を構成している個々の関数に着目し、微分を上手く使って原始関数が明らかに分かるような形に変形していく」事になります。
まずxexという関数について見てみましょう。これは部分積分の公式を適用して計算ができます。まず(d/dx)ex=exである事から部分積分の公式を使える形である事に着目します。具体的に不定積分を計算すると次の通りです。(最後の結果に加えてあるCは任意定数です。)
$$\int xe^xdx=\int x\left(\frac{d}{dx}e^x\right)dx=xe^x-\int \left(\frac{d}{dx}x\right)e^xdx$$
$$=xe^x-\int e^xdx=xe^x -e^x +C$$
得られた結果が本当にxexの原始関数なのかを確かめると、
(d/dx)(xex-ex)=ex+xex-ex=xex となっていますので大丈夫という事になります。
部分積分の公式自体が積の微分に由来にする関係式であるわけですが、
結果の式も「積の形」の項をを含むものになっています。
部分積分を使って府定積分を計算すると必ずそうなるというわけではありませんが、
元々の積分対象が積の形である時に部分積分法によって原始関数を導出すると、結果の式も積の形を含む場合も少なからずあるという事です。また、公式の形に由来して結果が2項以上の和や差になる事も多いのが特徴です。

定積分の場合は、例えば積分区間が [0, 1] であれば次のようにします。
$$\int_0^1 xe^xdx=\int_0^1 x\left(\frac{d}{dx}e^x\right)dx=\left[xe^x\right]_0^1-\int_0^1 \left(\frac{d}{dx}x\right)e^xdx$$
$$=e–\int_0^1 e^xdx=e-\left[e^x\right]_0^1=e-(e-1)=1$$
不定積分で最後の結果の原始関数を出してから、積分区間の端点を代入して計算しても同じ結果です。
(任意定数の部分は定積分では必ずC-C=0になって無くなります。)
次にx2exの不定積分は、部分積分の公式を2回使って計算をします。
あるいは、xexの不定積分が分かっている前提なら、それも途中で直接的に計算に出てくるので結果を利用できます。ここではそれで計算します。もしxexの不定積分の結果が不明な状態であればそこで2度目の部分積分を行うわけです。
$$\int x^2e^2dx=\int x^2\left(\frac{d}{dx}e^x\right)dx=x^2e^x-\int \left(\frac{d}{dx}x^2\right)e^xdx$$
$$x^2e^x-2\int xe^xdx=x^2e^x-2(xe^x -e^x)+C$$
$$=(x^2-2x+2)e^x+C$$
このように見ると、xsinxなども同様に部分積分の公式で計算できる事が分かります。
その場合は、sinx=(d/dx)(-cosx)のように考えます。
$$\int x\sin xdx=\int x\left(-\frac{d}{dx}\cos x\right)dx=x(-\cos x)-\int \left(\frac{d}{dx}x\right)(-\cos x)dx$$
$$=-x\cos x+\int \cos x dx=–x\cos x+\sin x +C$$
結果が合っているか確かめると、
(d/dx)(-xcosx+ sinx)=-cosx+xsinx+cosx=xsinx となります。
よって、大丈夫という事になります。
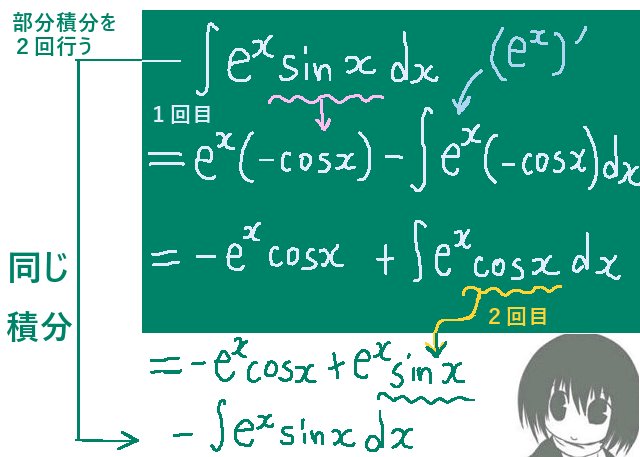
では、exsinxのような場合はどうでしょうか。これに関しては、実は部分積分を複数回行っても原始関数が直接的に分かる形には変形ができません。しかし、sinxとcosxに対して微分を行うとsinx→cosx→-sinx→-cosx→sinxのように周期的に同じ形になるので、部分積分で計算を進めた後に簡単な方程式を解く形で原始関数を導出できます。
$$\int e^x\sin x dx=\int \left(-\frac{d}{dx}\cos x\right)e^xdx=-e^x\cos x-\int (-\cos x)\left(\frac{d}{dx}e^x\right)dx$$
$$=-e^x\cos x+\int e^x\cos xdx=-e^x\cos x+\int e^x\left(\frac{d}{dx}\sin x\right)dx$$
$$=-e^x\cos x+e^x\sin x-\int \sin x\left(\frac{d}{dx}e^x\right)dx$$
$$=-e^x\cos x+e^x\sin x-\int e^x\sin xdx$$
この段階でまだ残っている不定積分の項は「最初の不定積分の符号だけ変えたもの」なので、
「方程式を解く形」で原始関数が分かる形になるパターンなのです。
これを不定積分の項に関して解いて、任意定数(C0およびC)も加えると次のようになります。
$$\int e^x\sin x dx=-e^x\cos x+e^x\sin x-\int e^x\sin xdx\hspace{2pt}となっているので$$
$$2\int e^x\sin x dx=-e^x\cos x+e^x\sin x +C_0$$
$$よって、\int e^x\sin x dx=\frac{e^x}{2}\left(-\cos x+\sin x\right)+C$$
ここでの任意定数の扱い方についてはそんなに気にしなくていい程度の事項ではありますが、
一応詳しく見るのであれば考えている関数の原始関数の1つをF(x)として、
2つの任意定数 C1とC2(別々の値を取り得る)を考えます。すると、
F(x)+C1=-excosx+exsinx+F(x)+C2で、
C1―C2=0とおけばそれ自体が任意の実数を表し得る、つまり任意定数となるので
2F(x)=ex(-cosx+ sinx)+C0 というようになります。
また、同じくそれ程気にする事項ではありませんが、最後にC=C0/2と考えて
F(x)=(ex/2)(-cosx+ sinx)+Cとしています。
結果が合っているか確かめると、
(d/dx){(ex/2)(-cosx+ sinx)}=(ex/2)(-cosx+ sinx)+(ex/2)(sinx+cosx )=exsinxとなっていて大丈夫である事が分かります。
「xの微分」が1として隠れている例
同じように部分積分の公式を使って原始関数を探す形で積分を計算する例として、ある関数に「xの微分」つまり(d/dx)x=1が乗じられていると見て部分積分の公式を適用する事があります。
これは一見すると数学上だけの技巧的な手段に思えるかもしれませんが、対数関数などの基本的な初等関数の原始関数を見つけるにあたっても重要な計算ですので知っておくと便利です。
比較的重要な次の2つの例で計算をしてみます。
2つのうち後者のほうの例は、置換積分によっても積分を計算できます。
- ln x(=logex)
- \(\sqrt{a^2-x^2}\) (定義域は|a| ≧ |x|の範囲)
ここで扱う対数関数は自然対数として考える対数であり、自然対数関数とも呼びます。
「ログナチュラル」と読む事もある lnxと書く表記方法をここでは使います。
まずln xについて、これをln x={(d/dx)x} lnxと考えるなら。対数関数の微分のほうについては(d/dx)ln x=1/xですので積分は部分積分法により上手く行きそうだと予想するわけです。
$$\int \mathrm{ln}x \hspace{1pt}dx=\int\left(\frac{d}{dx}x\right)\mathrm{ln}x \hspace{1pt}dx$$
$$=x\mathrm{ln}x-\int x\left(\frac{d}{dx}\mathrm{ln}x\right)dx=x\mathrm{ln}x-\int x\cdot\frac{1}{x}dx$$
$$=x\mathrm{ln}x-\int dx=x\mathrm{ln}x-x+C$$
$$\left(\int dx\hspace{2pt}は\hspace{2pt}\int 1 dx\hspace{2pt}の事です。\right)$$
結果が正しいか微分して確認すると、
(d/dx)(xlnx-x)=lnx+x・(1/x)-1=lnx+1-1=lnxとなり、
合っている事が分かります。

次に、比較的計算は込み入りますが後者のほうの例\(\sqrt{a^2-x^2}\) の積分についてです。置換積分でも積分を計算できますが、部分積分を使うと実は一般的な原始関数の形が分かります。結論を先に言うと、この関数の積分は逆正弦関数 Arcsinxを含んだ形で表されます。(逆三角関数の1つです。)
|x| <1のもとで
(d/dx)Arcsinx=1/\(\sqrt{1-x^2}\)であり、
(d/dx)Arcsin(x/a)=1/\(\sqrt{a^2-x^2}\)(a≠0の時)なので、
その形を作れないかどうかを考えると計算が理解しやすくなります。
自然対数関数に対する積分の時と同じく、xの微分としての「1」が隠れていると見ます。
$$\int \sqrt{a^2-x^2}dx=\int \left(\frac{d}{dx}x\right)\sqrt{a^2-x^2}dx=x\sqrt{a^2-x^2}-\int x\left(\frac{d}{dx}\sqrt{a^2-x^2}\right)dx$$
$$=x\sqrt{a^2-x^2}-\int x\left(-2x\cdot\frac{1}{2}\frac{1}{\sqrt{a^2-x^2}}\right)dx$$
$$=x\sqrt{a^2-x^2}+\int \frac{x^2}{\sqrt{a^2-x^2}}dx=x\sqrt{a^2-x^2}+\int \frac{x^2-a^2+a^2}{\sqrt{a^2-x^2}}dx$$
$$=x\sqrt{a^2-x^2}+\int \left(\frac{a^2}{\sqrt{a^2-x^2}}-\sqrt{a^2-x^2}\right)dx$$
a≠0の時は、積分の中の第1項をx/a を変数とする Arcsin(x/a)で表せます。
また、その段階で式を整理すると実は「積分の項に関して移項して解く」タイプの形になっている事が分かるので積分の結果が分かります。
$$a\neq 0 の時、\int \sqrt{a^2-x^2}dx=x\sqrt{a^2-x^2}+a^2\mathrm{Arcsin}\frac{x}{a}-\int \sqrt{a^2-x^2}dxであるので$$
$$2\int \sqrt{a^2-x^2}dx=x\sqrt{a^2-x^2}+a^2\mathrm{Arcsin}\frac{x}{a}+C_0$$
$$よって、\int \sqrt{a^2-x^2}dx=\frac{1}{2}\left(x\sqrt{a^2-x^2}+a^2\mathrm{Arcsin}\frac{x}{a}\right)+C$$
細かい事ですがもしa=0であれば定義域は|a| ≧ |x|でしたから、定義域はx=0となり関数の値も0です。従って、もしそれをxで積分をするとしてもその値も0となります。ですので積分を考える場合には最初から|a|>0として考える、という事もできます。
以上の2例については一応結果をまとめておきましょう。
(結果を覚える必要があるというよりは、「部分積分法を使えばこのように結果を出せる」という事のほうが重要と思われます。)
自然対数関数の不定積分は次のようになります。
$$\int \mathrm{ln}x \hspace{1pt}dx=x\mathrm{ln}x -x +C$$
\(\sqrt{a^2-x^2}\) の不定積分は a≠0 の時は次のようになります。
(a=0 の時はxも関数値も0となるので、不定積分も0)
$$\int \sqrt{a^2-x^2}dx=\frac{1}{2}\left(x\sqrt{a^2-x^2}+a^2\mathrm{Arcsin}\frac{x}{a}\right)+C$$
$$\left(例えばa=1の場合は\int \sqrt{1-x^2}dx=\frac{1}{2}\left(x\sqrt{1-x^2}+\mathrm{Arcsin}x\right)+C\right)$$
これらはいずれも「隠れた1」が関数に乗じられていると見て、
部分積分の公式を適用して計算すると結果が得られるタイプの不定積分です。
\(\sqrt{a^2-x^2}\) の不定積分の結果について、
計算が合っているかの検証用に結果の式を微分するのは少し面倒ですが
最初の項が積の微分で2項に分離し、全体の合計が元の関数になる事を確認できます。
$$\frac{d}{dx}\left\{\frac{1}{2}\left(x\sqrt{a^2-x^2}+a^2\mathrm{Arcsin}\frac{x}{a}\right)\right\}$$
$$=\frac{1}{2}\left(\sqrt{a^2-x^2}+x\cdot(-2x)\cdot\frac{1}{2} \frac{1}{\sqrt{a^2-x^2}}+\frac{a^2}{\sqrt{a^2-\frac{x^2}{a^2}}}\right)$$
$$=\frac{1}{2}\left(\sqrt{a^2-x^2}-\frac{x^2}{\sqrt{a^2-x^2}}+\frac{a^2}{\sqrt{a^2-x^2}}\right)$$
$$=\frac{1}{2}\left(\sqrt{a^2-x^2}+\frac{a^2-x^2}{\sqrt{a^2-x^2}}\right)$$
$$=\frac{1}{2}\left(\sqrt{a^2-x^2}+\sqrt{a^2-x^2}\right)=\frac{1}{2}\cdot 2\sqrt{a^2-x^2}=\sqrt{a^2-x^2}$$
応用例1:テイラー展開を部分積分から導出する方法
関数のテイラー展開と、その特別な場合であるマクローリン展開は微分係数を使った多項式の形により関数を近似する関係式で、数学上も物理等での応用においても非常に有用でよく使われる式です。
例えば自然対数の底による指数関数exのマクローリン展開(「x=0における」テイラー展開)は次のような無限級数になります。(この無限級数は収束します。)
$$e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots+\frac{x^n}{n!}+\cdots$$
この式の出し方は色々あるのですが、実は部分積分の公式を使って導出可能です。exの式を見ると3!とか4!とかの階乗の部分が一体なぜ出て来るのか疑問に思われるかもしれませんが、部分積分の観点から言うとその部分の根拠は関数xnの微分です。正確に言えばその積分をする事で出てくるので自然数の係数は全て分母についています。
少し工夫は必要ですが、ex =「x=0の値」+「x=0での微分係数」x+「x=0での2階導関数の微分係数」x2+「x=0での3階導関数の微分係数」x3+・・・のような形にする事を考えます。
つまり、積分の計算をするために部分積分の公式を使う時と違って、式の項をどんどん増やしていきます。以下、少し詳しく丁寧に見ていきます。
まず、e0=1である事を踏まえて次のようにします。
$$e^x=1+\int_0^xe^td=\hspace{5pt}\left(=1+\large{\left[e^t \right]_0^x}=1+e^x-1\right)$$
ここで、積分の項は「xの関数」として扱いたいので変数xと「積分変数t」を敢えて分けて考えています。(この考え方は元々の定積分や不定積分を定義dする段階で実は存在します。)
次に定積分の項に関して部分積分の結果を考えながら、「t=xを代入すると0になり、t=0を代入すると-xになる関数」を考えます。ちょっと妙な気もするかもしれませんが、これはt-xという関数が該当します。これにetが乗じられた(t-x)etが部分積分の結果として出てくる事を予想します。
そこで、積分変数tに関して1=(d/dt)(t-x)が乗じられていると見ます。
ここで、xをtに関する定数とするので(d/dt)x=0です。対数関数の積分を部分積分によって計算する時と同じ考え方です。
「積分に関してはxを定数と考える」というのは少し分かりにくいかもしれませんが、
まずxが「定数」だと考えて積分の結果を出してから
「そのxの値がどの実数値でも成立するので変数としてみなせる」と考える事もできます。
例えばx=3とか7とかいったてきとうな定数を考えてみて、
「0から7までの定積分」などを計算してみるとよいかもしれません。
その場合、定数に対する微分の結果は0ですから、
(d/dt)(t-7)=(d/dt)t=1というふうに確実に計算の過程を見れます。
「隠れた1がある」として考えた時、計算は次のようになります。
$$e^x=1+\int_0^xe^td=1+\int_0^x\left\{\frac{d}{dt}(t-x)\right\}e^tdt$$
$$=1+\large{\left[(t-x)e^t\right]_0^x}-\int_0^x(t-x)\left(\frac{d}{dt}e^t\right)dt$$
$$\large{=1+\{0-(-x)e^0\}-\int_0^x(t-x)e^tdt}$$
$$\large{=1+x+\int_0^x(x-t)e^tdt}$$
さらに、この後も同じような部分積分を続けて項を増やします。
ただし、ここから先は次のように考えます。
- 部分積分の2項目で必ずマイナス符号が出てくる事をあらかじめ予測する
- 操作を続けて行くにあたり、「最後の項が0に収束する」事を期待する
そこで、部分積分の操作を続けて行くと「分母の値が大きくなる」事を期待してtではなくt2の微分が乗じられている形の項を考えます。そのような項の条件を整理しておきます。
- xを定数としてtで微分すると-(t-x)=x-tになる
- t=xで0になる
- t=0でxの関数になる
すると、具体的には-(x-t)2/2の形を考えると、
xを定数扱いとしてtで微分すると
-{-2(x-t)}/2=x-tとなるので、まず微分に関する条件は満たします。
また t=xでは-(x-t)2/2=0であり、
t=0としてマイナス符号を付けると-{-(x-0)2/2}=x2/2です。
そこで、上記の積分の項において
-(x-t)2/2のtによる微分とetが乗じられていると見て部分積分を続けます。
$$\large{e^x=1+x-\int_0^x(x-t)e^tdt=1+xe^x+\int_0^x\left\{\frac{d}{dt}\frac{-(x-t)^2}{2}\right\}e^tdt}$$
$$=1+x+\large{\left[-\frac{(x-t)^2}{2}e^t\right]_0^x}-\int_0^x\frac{-(x-t)^2}{2}\left(\frac{d}{dt}e^t\right)dt$$
$$\large{=1+x-\left\{\frac{-(x-0)^2}{2}e^0\right\}-\int_0^x\frac{-(x-t)^2}{2}e^tdt}$$
$$\large{=1+x+\frac{x^2}{2}+\int_0^x\frac{(x-t)^2}{2}e^tdt}$$
定積分の項に対してさらに部分積分を続けます。
微分して(x-t)2/2になる関数を考えると-(x-t)3/(2・3)が該当するので、
etに対して(d/dt){-(x-t)3/(2・3)}=(d/dt){-(x-t)3/(3!)}
が乗じられていると見ます。
そしてその次は、etに対して
(x-t)3/(3!)=(d/dt){-(x-t)4/(4!)}が乗じられていると見ると、
部分積分によりx4/(4!)の項が付け加わります。
$$\large{e^x=1+x+\frac{x^2}{2}+\int_0^x\frac{(x-t)^2}{2}e^tdt}$$
$$\large{=1+x+\frac{x^2}{2}+\int_0^x\left\{\frac{d}{dt}\frac{-(x-t)^3}{3!}\right\}e^tdt}$$
$$\large{ =1+x+\frac{x^2}{2}+\left[\frac{-(x-t)^3}{3!}e^t\right]_0^x-\int_0^x\frac{-(x-t)^3}{3!}\left(\frac{d}{dt}e^t\right)dt }$$
$$\large{ =1+x+\frac{x^2}{2}-\left\{\frac{-(x-0)^3}{3!}e^0\right\}-\int_0^x\frac{-(x-t)^3}{3!}e^tdt }$$
$$\large{ =1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\int_0^x\frac{(x-t)^3}{3!}e^tdt }$$
$$\large{ =1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\int_0^x\left\{\frac{d}{dt}\frac{-(x-t)^4}{4!}\right\}e^tdt }$$
$$\large{ =1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\left[\frac{-(x-t)^4}{4!}e^t\right]_0^x-\int_0^x\frac{-(x-t)^4}{4!}\left(\frac{d}{dt}e^t\right)dt }$$
$$\large{ =1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\frac{x^4}{4!}+\int_0^x\frac{(x-t)^4}{4!}e^tdt }$$
ここでは計算を少し詳しく書いていますが、要所以外は省略してももちろん可です。
これの次は etに
(x-t)4/(4!)=(d/dt){-(x-t)5/(5!)}が乗じられていると見て
これまで同様にしてx5/(5!)の項が付け加わります。
その後も部分積分の計算をずっと繰り返していきます。
このようにして
ex=1+x+x2/2+x3/(3!)+x4/(4!)+x5/(5!)+・・・+「最後の項」
が出てくるわけです。結果だけ見ると不思議な事ですが指数関数を多項式の形に変形できています。
この、有限の値の「最後の項」を含む段階の関係式をテイラー公式と言います。
ex の
x= 0における exのテイラー公式は次式です。$$e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots+\frac{x^n}{n!}+\int_0^x\frac{(x-t)^n}{n!}e^tdt $$(他の方法でもテイラー公式を導出した時は最後の項の形だけ異なる形になります。)
部分積分を行う積分範囲をt=aからt=xとした場合は、etの微分は何階の導関数でも形が変わらずetであり、部分積分をした時にt=aを代入した(xーa)kea/k!の形の項が残る事に注意すると、次式です。$$e^x=e^a+e^a(x-a)+e^a\frac{x^2}{2}+e^a\frac{(x-a)^3}{3!}+\cdots+e^a\frac{(x-a)^n}{n!}+\int_0^x\frac{(x-t)^n}{n!}e^tdt $$
$$=e^a\left\{1+(x-a)+\frac{x^2}{2}+\frac{(x-a)^3}{3!}+\cdots+\frac{(x-a)^n}{n!} \right\}+\int_0^x\frac{(x-t)^n}{n!}e^tdt $$
指数関数以外でも同様の式を作れます。
関数f(x)のx=aにおけるテイラー公式を部分積分で計算すると次式です。
$$f(x)=f(a)+f^{\prime}(a)(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2+\cdots+\int_a^x\frac{(x-t)^n}{n!}\frac{d^nf(t)}{dt^n}dt$$
$$\left(\frac{df}{dx}=
f^{\prime}(x)
\hspace{10pt}
\frac{d^2f}{dx^2}=f^{\prime\prime}(x)
\hspace{2pt}と表記されます。\right)$$
最後の項(剰余項)がn→∞で0に収束する時には式全体は収束する無限級数となって、それが関数のテイラー展開と呼ばれ、「x=0におけるテイラー展開」はマクローリン展開とも呼ばれます。指数関数や三角関数は、どの実数の値においても剰余項がn→∞で0に収束するので全実数の範囲でテイラー展開が可能である事を証明できます。
ここでの導出方法における定積分の項の扱いについては、
より正確に
数学的帰納法として証明を書くなら次のようになります。
示すべき命題は任意の自然数nに対して次式が成立する事です。
$$e^x=\left(\sum_{k=0}^n\frac{x^k}{k!}\right)+\int_0^x\frac{(x-t)^n}{n!}e^tdt$$
$$
\left(=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots+\frac{x^n}{n!}+\int_0^x\frac{(x-t)^n}{n!}e^tdt\right)$$
シグマ記号で書いた部分について、階乗の定義により0!=1です。
n=1の時には次のようになるので成立しています。(n=0の時から考えても可です。)
$$e^x=1+e^x-1=1+\int_0^xe^tdt=1+\int_0^x\left\{\frac{d}{dt}(t-x)\right\}e^tdt$$
$$=1+\large{\left[(t-x)e^t\right]_0^x}-\int_0^x(t-x)\left(\frac{d}{dt}e^t\right)dt$$
$$=1+\frac{x}{1!}+\int_0^x\frac{(x-t)}{1!}e^tdt$$
(n=0から始める場合は\(\large{e^x=1+\int_0^xe^tdt=\frac{x^0}{0!}+\int_0^x\frac{(x-t)^0}{0!}e^tdt}\) であり、証明すべき式は成立しています。
ですが、分かりやすさのためにここではn=1から始めています。)
n=kの時に証明すべき式が成立すると仮定し、
定積分の項に対して部分積分の公式を適用すると次のようになります。
$$\large{ e^k=1+x+\frac{x^2}{2}+\cdots+\frac{x^k}{k!}+\int_0^x\frac{(x-t)^k}{k!}e^tdt }$$
$$\large{ =1+x+\frac{x^2}{2}+\cdots+\frac{x^k}{k!}+\int_0^x\left[\frac{d}{dt}\left\{\frac{-(x-t)^{k+1}}{(k+1)!}\right\}\right]e^tdt }$$
$$\large{ =1+x+\frac{x^2}{2}+\cdots+\frac{x^k}{k!}+\left[\frac{-(x-t)^{k+1}}{(k+1)!}e^t\right]_0^x}$$
$$\large{-\int_0^x\frac{-(x-t)^{k+1}}{(k+1)!}\left(\frac{d}{dt}e^t\right)dt }$$
$$
\large{ =1+x+\frac{x^2}{2}+\cdots+\frac{x^k}{k!}+\frac{x^{k+1}}{(k+1)!}+\int_0^x\frac{(x-t)^{k+1}}{(k+1)!}e^tdt }$$
よってn=k+1の時も確かに成立するので、
任意の自然数nに対して証明すべき式(x=0におけるexのテイラー公式)が成立します。
指数関数に限らず、n階までの微分が可能な関数は同じ計算でテイラー公式を導出可能です。
また、部分積分法を使う計算以外にもテイラー公式を導出する方法は存在します。その場合は最後の剰余項が異なる形になりますが、指数関数や三角関数においてはその時の剰余項もn→∞で0に収束し、部分積分で計算した時と同じく全実数の範囲でテイラー展開が可能です。
応用例2:近似式の導出(スターリングの公式での例)
スターリングの公式は、十分大きい自然数に対する階乗N!についての
自然対数 ln(N!)に対する近似式です。
この近似式の導出過程には主に2つあって1つはガンマ関数を使う方法ですが、
もう1つは階乗に対する対数を近似的な「面積」と見て、自然対数関数の積分で近似する方法です。
ところで前述のように、e を底とする単独の自然対数関数の積分は部分積分によって計算するやり方が見やすいのでした。ここでの使用例は、割と普通に定積分の計算を普通にするために部分積分の公式を使うというものになります。
そこで、積分を考えたところから部分積分を使って具体的に導出過程を見てみます。積分区間は、十分大きい自然数Nと、何か小さい実数 a( >0)を使って [a, N +a]で考えます。
$$\mathrm{ln}(N!)≒\int_a^{N+a}\mathrm{ln}x\hspace{2pt}dx=\int_a^{N+a}\left(\frac{d}{dx}x\right)\mathrm{ln}x\hspace{2pt}dx$$
$$=\large{[x\mathrm{ln}x]_a^{N+a}}-\int_a^{N+a}x\cdot\frac{1}{x}\hspace{2pt}dx$$
$$=\large{[x\mathrm{ln}x]_a^{N+a}}-\int_a^{N+a}dx=\large{[x\mathrm{ln}x+x]_a^{N+a}}$$
$$=(N+a)\mathrm{ln}(N+a)+(N+a)-a\mathrm{ln}a-a=(N+a)\mathrm{ln}(N+a)+N-a\mathrm{ln}a$$
ここで、a が小さくてNは十分大きいとするとN+a ≒N と考えて、
また a ln a の項も他項に比べて小さく無視できるとします。
実際の近似ではNをそれほどを大きくとらなくても十分である時もあるのですが、
例えば分かりやすくNが1万で、aが0.1としましょう。
すると、
10000と10000.1の比較になりますが、
このような時には両者の差は十分小さいと見れるわけです。
すると、残った項により式を次のように近似できます。
$$\mathrm{ln}(N!)≒(N+a)\mathrm{ln}(N+a)-a\mathrm{ln}a+N≒N\mathrm{ln}N +N$$
これがスターリングの公式あるいはスターリングの近似式と呼ばれる近似式です。
主に統計力学などで使用されます。
応用例3:変分問題での例
(オイラー・ラグランジュ方程式)
理論物理学で非常に重要となる変分に関する基本的な問題(と言っても決して易しくありませんが)であるオイラー・ラグランジュ方程式(あるいは「オイラー方程式」)の導出過程では、実は計算としては部分積分を使います。しかも、使うと計算が便利というだけでなく関係式を導出するにあたって肝心となる式の変形を担っています。これは数学の問題でもありますが、むしろ物理学等のほうに関連が深い話となります。
部分積分を使う箇所に絞って取り上げると、次のような計算問題です。
xについての閉区間 [a, b]があり、η(a)=η(b)=0を満たす任意の関数η(x)がある。
また、xについての関数F1(x) と F2(x)があり、
次の式が成立しているという。
$$\int_a^b\left\{\eta(x)F_1(x)+\frac{d\eta(x)}{dx}F_2(x)\right\}dx=0$$
この時、実はη(x)を含まない形でF1(x) と F2(x)に関する微分方程式が成立しますが、
それは具体的にどのような関係式となりますか。
具体的な関数の形が一部の条件以外は何もありませんから、普通に定積分をこのまま計算するという事はできません。しかし、定積分の中身にη(x)という関数の導関数dη(x)/dxと、別の関数F2(x)の積の形が含まれている事に注意すると、部分積分の公式を使う事ができるのです。
そこで、(dη(x)/dx)F2(x) の項について部分積分の公式に当てはめて計算を進めてみます。
$$\int_a^b\frac{d\eta(x)}{dx}F_2(x)dx=\large{[\eta(x)F_2(x)]_a^b}-\int_a^b\eta(x)\frac{dF_2(x)}{dx}dx$$
$$=\eta(b)F_2(b)-\eta(a)F_2(a)–\int_a^b\eta(x)\frac{dF_2(x)}{dx}dx$$
$$\eta(a)=\eta(b)=0の条件により、\int_a^b\frac{d\eta(x)}{dx}F_2(x)dx=-\int_a^b\eta(x)\frac{dF_2(x)}{dx}dx$$
つまり、積分区間の端点における条件η(a)=η(b)=0がありましたから、
部分積分の行った後の第1項(値を代入する部分)は0となって「消える」わけです。
すると、実質的には元の定積分の中身に対して符号を入れ換えたうえで「微分する対象を入れ換える」
という変形ができた事も意味します。
このようにできたりする事が、物理等で部分積分が要所の計算で意外に活用される大きな理由の1つです。つまり、0になってしまう項や0に近似できる項を分離して「消してしまう」事で、関数の全体の形を変形する手段として部分積分法が使われる事があります。
ここでの例は閉区間内の定積分ですが、無限大で関数が0に収束する条件を使う事で部分積分法を適用した時の1つの項を「消す」という場合もあります。後述の量子力学での波動関数などはその例です。
部分積分を行っていない項と合わせると、次のようになります。
$$\int_a^b\left\{\eta(x)F_1(x)+\frac{d\eta(x)}{dx}F_2(x)\right\}dx=\int_a^b\left\{\eta(x)F_1(x)-\eta(x)\frac{dF_2(x)}{dx}\right\}dx$$
$$=\int_a^b\eta(x)\left(F_1(x)-\frac{dF_2(x)}{dx}\right)dx$$
$$今、\int_a^b\left\{\eta(x)F_1(x)+\frac{d\eta(x)}{dx}F_2(x)\right\}dx=0という条件であり、$$
$$\eta(x)は端点での条件を満たす「任意」の関数形なのでF_1(x)-\frac{dF_2(x)}{dx}=0$$
つまり、F1(x)-(d/dx)F2(x)=0が、η(x)を含まない形でのF1(x)とF2(x)が満たす微分方程式である、という事になります。(※η(x)が「任意」でなかったら、積分全体が0であるからといって被積分関数またはその一部が0だとは言えませんので注意も必要です。)
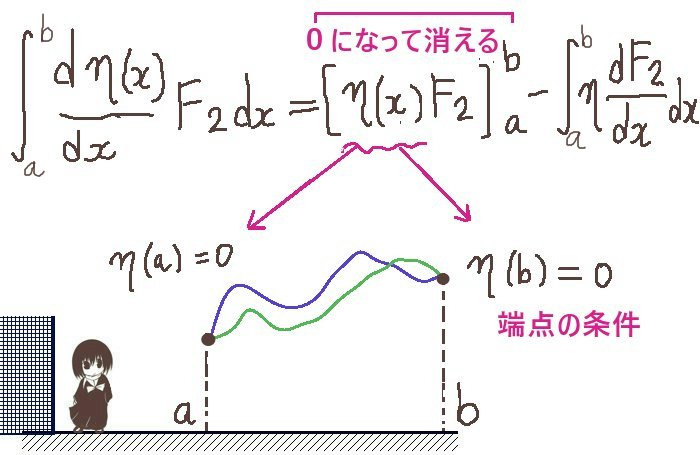
変分問題とオイラー・ラグランジュ方程式
上記の問題の元の形を一応記しておくと次のようになります。
比較関数η(x)を使わないで内容としては同じ問題を考える場合もあります。
■問題:
閉区間 [a, b] において関数y=y(x)があって、sを実数としてy(x)にsη(x)という関数を付け加えたものを考える。(関数形自体を自由に変形するという事。)
y(a) および y(b) は定数で、η(a)=η(b)=0の条件のもと、
x,y,y’(=dy/dx)を変数として表される別の関数F(x,y,y’)があるという。
その条件下で [a, b] におけるF(x,y,y’)に対するxでの定積分I[y]を最小にするyの関数形が存在する時、F(x,y,y’)についてη(x)を含まない形で成立する式は何ですか。
【答え:微分方程式 ∂F/∂y-d/dx(∂F/∂y’)=0】
$$y(a)およびy(b)が定数であり、\eta (a)=\eta (b)=0の条件のもと、$$
$$I[y]=\int_a^bF(x,y,y^{\prime})dxを最小にするy(x)の関数形に対して次式が成立します。$$
$$\frac{\partial F}{\partial y}-
\frac{d}{dx}\left(\frac{\partial F}{\partial y^{\prime}}\right)=0$$
この「オイラー・ラグランジュ方程式」は式に偏微分を含みますが、微分方程式としてはxに関する「常微分方程式」になります。yもdy/dxも、最終的にはxの関数として表せるためです。ただし実際問題としてはyなどをそのままの形で残して扱う場合も多いです。
応用例4:遠方で0になる関数の積分(量子力学など)
変分問題と同部類の部分積分の応用例としては、他にも
無限遠で0に収束する関数の積に対する(-∞,+∞)の範囲で行う積分などがあります。
量子力学で扱う波動関数(あるいは「状態」を表す関数)に対する積分計算はその例です。
波動関数の場合で言うと、無限遠と言っても正確には「ミクロのスケールから見て十分遠方の位置」を指しており、つまりメートル単位の遠方はそのような「十分な遠方」に該当します。ただし数式的にはとりあえず、それを無限大として扱うわけです。
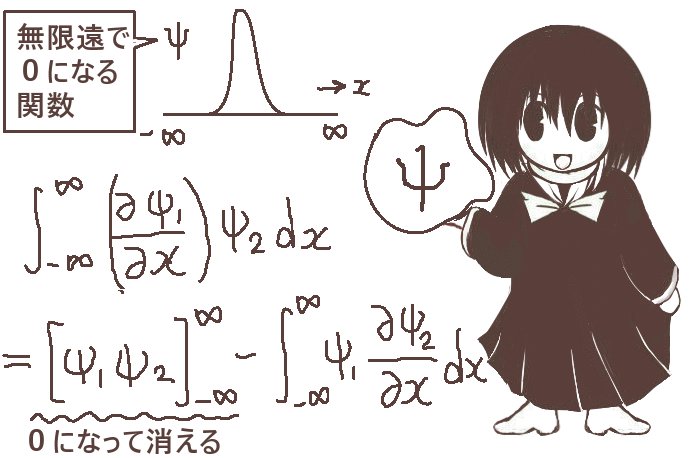
そのような時、2つの波動関数Ψ1とΨ2があるとします。(あるいは波動関数でなくても、遠方での条件が類似するような関数。)そのうちの片方の位置による微分(偏微分)による導関数と、もう片方の積(∂Ψ1/∂x)Ψ2を考えて積分を(-∞,+∞)で行うとしましょう。部分積分に関しては積の微分を根拠にした公式ですので、偏微分で行っても1変数の微分でも同じ形になります。また、量子力学では波動関数は一般的には複素数関数ですが、やはり部分積分は適用可能です。
(∂Ψ1/∂x)Ψ2に対する積分を、部分積分によって変形すると次のようになります。
$$\int_{-\infty}^{\infty}\frac{\partial \psi_1}{\partial x}\psi_2 dx=\large{[\psi_1\psi_2]_{-\infty}^{\infty}}-\int_{-\infty}^{\infty}\psi_1\frac{\partial \psi_2}{\partial x} dx$$
$$=-\int_{-\infty}^{\infty}\frac{\partial \psi_2}{\partial x} \psi_1dx$$
無限遠方でΨ1とΨ2は0と考えているので、部分積分を行った後の第1項は0になって「消える」わけです。すると、符号の入れ替えはありますが「微分する対象が入れ替わった積分」として式を変形できるという結果を得ます。
これを利用して近似式を考えたり、微分を含む演算子の作用の関係を考察できたりします。
量子力学における波動関数でなくても、類似の条件の関数に対する積分を計算する時は部分積分による近似計算は全く同じように可能となります。ただしそういった条件の関数に対して上記のような積分を行う典型例としては、量子力学の波動関数を挙げる事ができるという事です。
ここでは簡単のために上記のような例で考えましたが、先ほど触れたように波動関数は一般に複素数関数ですので多くの場合では波動関数Ψに対する「共役」\(\overline{\psi}\)(概略としてはいわゆる複素共役)も考えて理論を展開します。
応用例5:ガンマ関数の関係式の導出
より数学的な話ですが、ガンマ関数(特殊関数の1つ)に対して成立する関係式
Γ(x+1)=xΓ(x)は、実は部分積分の公式を使った比較的簡単な直接計算によって導出されます。
ガンマ関数は次のようにそもそもが積分で表される関数です。定義域はx>0として必ず考えます。
そのため、積分区間の端点の「0」のほうも「0への極限を考える」という意味になります。
$$\Gamma(x)=\int_{0}^{\infty}t^{x-1}e^{-t}dt$$
定義域であるx>0における任意の実数xに対して、次の関係式が必ず成立します。$$\Gamma(x+1)=x\Gamma(x)$$ この関係式においてxが自然数である場合を敢えて考えて少し計算をすると、自然数に対するガンマ関数の値は階乗の形で表される事が分かります。
変数をx+1に置き換えたΓ(x+1)について、積分中の指数関数のほうに対して部分積分を考える事で変形ができます。(前述のxexのような関数の積分に対して部分積分を行う時と同じ考え方です。)
$$\Gamma(x+1)=\int_{0}^{\infty}t^xe^{-t}dt=\int_{0}^{\infty}t^x\left(\frac{d}{dt}-e^{-t}\right)dt$$
$$=\large{\left[-e^{-t}t^x\right]_0^{\infty}}-\int_{0}^{\infty}\left(\frac{d}{dt}t^x\right)\left(-e^{-t}\right)dt$$
$$=-\lim_{t\to\infty}\frac{t^x}{e^t}+\lim_{t\to 0}\frac{t^x}{e^t}+\int_{0}^{\infty}xt^{x-1}e^{-t}dt$$
$$\lim_{t\to\infty}\frac{t^x}{e^t}=0\hspace{2pt}であり、\hspace{2pt}\lim_{t\to 0}\frac{t^x}{e^t}=0\hspace{2pt}なので$$
$$\Gamma(x+1)=\int_{0}^{\infty}xt^{x-1}e^{-t}dt=x\int_{0}^{\infty}t^{x-1}e^{-t}dt=x\Gamma(x)$$
最後の箇所では、xはここでの積分においては定数扱いとなるので積分全体に乗じられる定数としています。(テイラー公式を部分積分で導出した計算と同じ考え方です。)
このような計算によって導出がされるわけで、Γ(x+1)=xΓ(x)の関係において
「1」という自然数がどこから出てくるのかというと、xを定数扱いする時に
「tによる微分計算でtxの指数が1減る事」つまり(d/dt)tx=tx-1という、微分の計算方法を知っていれば非常に単純な式に由来する事が分かります。
ここでも「xは定数扱い」としている事が重要で、
(d/dt)tx は (d/dx)txとは異なるのです。
(d/dx)tx をもし計算するなら、それは指数関数の微分になるので異なる結果となります。
$$\frac{d}{dt}t^a=t^{a-1}の計算をしていて、これは\frac{d}{dx}a^x=\mathrm{log}_ea^xとは異なります。$$
また、この計算では部分積分の公式を適用した時の第1項が0になる事(ここでは極限値として0)を利用しているとも言えるので、広い意味では前述の変分問題や波動関数に対する積分での部分積分法の使い方と同部類のものであるとも言えるでしょう。
上記の計算で少し分かりにくい所は、途中の極限の項が0に収束するという箇所でしょうか。
t→∞(無限大)だけでなくt→0の極限も考えている(定義域がx>0でt>0でもあるので)わけですが、いずれの場合も、tx/et(=txe-t)という関数についての
「任意の実数x>0に対する」t→0とt→∞の極限を考えています。
ただし、t→0の極限のほうは実質的に「tに0を代入」で済む話となり、xがいかなる値であっても極限値は0であるとすぐに分かります。
他方でt→∞の極限のほうも結論から言うと極限値は0となりますが、
数式的にはtx/et(=txe-t)という関数において
任意の実数x>0に対してt→∞の時 tx/et →0かどうか?を少し考える必要があります。
これは例えばx=2でもx=100でも、
t→∞の時に t2/et →0でありt100/et →0であるかという問題です。
この極限は、直感的にはtに対する指数がいかに大きくても、分母の指数関数のほうが最終的には圧倒的に大きくなるので「t→∞で0に収束する」と理解できます。
数式でそれを明確にする方法はいくつかありますが、例えばロピタルの定理という微積分での計算法を使うと、比較的簡単な計算によって任意のx>0についてtx/et のt→∞での極限が0になる事を示せます。