曲率円そのものについては高校ではあまり扱いませんが、内容としては高校数学のまとめのような所もあるので、高校数学としても勉強になる題材かもしれません。より一般的には、曲線・曲面論の初歩的な事項の1つになります。
曲線の曲がり具合と曲率円
平面上の曲線について、緩やかに曲がっているものもあれば、急激な曲がり方をしているものもあります。
その曲り方の度合いを定量的に調べる方法としては、まず微分によって傾きを調べる方法が1つあります。
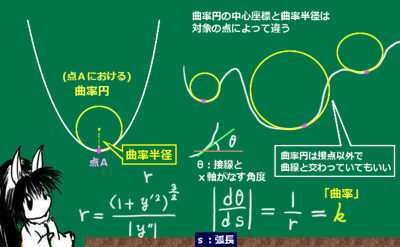
他方で、「曲線のある箇所に接する事のできる円の半径の最大値」によってその曲がり具合を調べる方法もあります。その目的で用意する円の事を「曲率円」と言い、曲率円の半径の事を「曲率半径」と言います。
この曲率円は、調べようとしている点以外の場所で曲線と交わっていても構いません。
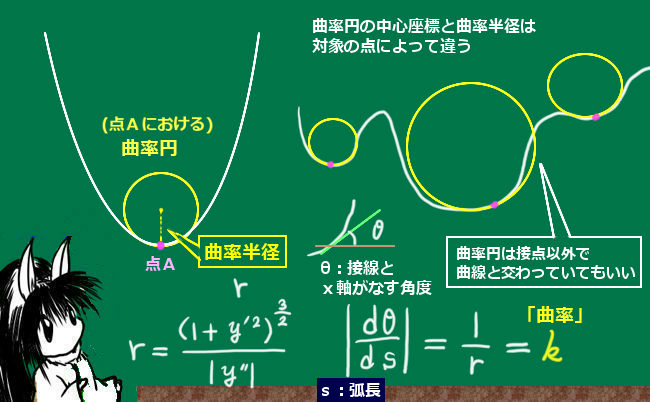
曲率円の中心座標と曲率半径の公式
曲線上のある点に注目した時には、
「曲率円の中心座標と半径(「曲率半径」)は曲線を表す関数の2階までの導関数(微分)の微分係数を使って表す事ができる」という公式が存在します。
曲線がy=f(x)と表される時、x=cでの曲率円の中心座標(a,b)と曲率半径rは次のように表されます。f(c)=fc、f'(c)=f’c、f”(c)=f”cと表記しています。$$中心座標:a=c-\frac{(1+f_c’\hspace{1pt}^2)f_c’}{f_c’\hspace{1pt}’}\hspace{15pt}b=f_c+\frac{(1+f_c’\hspace{1pt}^2)}{f_c’\hspace{1pt}’}$$
$$曲率半径:r=\frac{(1+f_c’\hspace{1pt}^2)^{\large{\frac{3}{2}}}}{|f_c’\hspace{1pt}’|}$$
【これらは、関数の形としてxとy、y’、y”の形で書いても成立します。】
曲率半径の式の分母に絶対値記号がつくのは、単純に半径がプラスの値であるという意味です。
中心座標に関しては、マイナスの値である事もあり得ます。
◆証明:円の式(x-a)2+(y-b)2=r2と、両辺の1階微分および2階微分の3式を使います。
微分なし:(x-a)2+(y-b)2=r2
1階微分:2(x-a)+2y’ (y-b)=0 ⇔ (x-a)+y’ (y-b)=0
【yの所は合成関数の微分公式使用】
2階微分:1+y”(y-b)+y’2=0
【yの所は積の微分公式使用】
実は、これらの式からa、b、rについて解くというだけで証明は十分です。
◆上記3式は単独で存在する円のについて成立する式と全く同じ形ですが、ここではx=cで、yの値もy=f(c)で固定されていると考えてa、b、rの値を出そうとしているわけです。
【円の導関数を出す目的であれば、a、b、rが定数であって、y’をxの関数あるいはxとyの関数で表します。】
以下、上記3式に、x=cを代入し、yにはy=f(c)を代入している【煩雑さを避けるためにyのままで表記しておきます】と考えます。
まず、2階微分の式からbをすぐに出せます。
$$1+y’\hspace{1pt}'(y-b)+y’\hspace{1pt}^2\Leftrightarrow y-b=-\frac{1+y’\hspace{1pt}^2}{y’\hspace{1pt}’}\Leftrightarrow b=y+\frac{1+y’\hspace{1pt}^2}{y’\hspace{1pt}’}$$
◆ある点で円に接する曲線は直線も含めてたくさんあり得ますが、
曲線の2階微分の微分係数まで決定している状況であれば、その曲線に接する事のできる円の中心のy座標は確定してしまう事を意味します。
次に、y-bを1階微分の式に代入します。
$$(c-a)+y’\left(-\frac{1+y’\hspace{1pt}^2}{y’\hspace{1pt}’}\right)=0\Leftrightarrow a=c-\frac{(1+y’\hspace{1pt}^2)y’}{y’\hspace{1pt}’}$$
◆円の2階微分の式から中心のy座標は確定していたわけですが、
1階微分の式、つまり「接する」という条件からx座標も任意であるわけではなく、結論は1つに決まるという事です。
この式からc-aも分かるので、y-bと合わせて微分前の式に代入してrを出します。
$$(c-a)^2+(y-b)^2=r^2\Leftrightarrow \left(y’\cdot\frac{1+y’\hspace{1pt}^2}{y’\hspace{1pt}’}\right)^2+\left(-\frac{1+y’\hspace{1pt}^2}{y’\hspace{1pt}’}\right)^2=r^2$$
$$\Leftrightarrow r^2=\frac{y’\hspace{1pt}^2
(1+y’\hspace{1pt}^2)^2+(1+y’\hspace{1pt}^2)^2}{y’\hspace{1pt}’\hspace{1pt}^2}=\frac{(1+y’\hspace{1pt}^2) (1+y’\hspace{1pt}^2)^2}{y’\hspace{1pt}’\hspace{1pt}^2}=\frac{(1+y’\hspace{1pt}^2)^3}{y’\hspace{1pt}’\hspace{1pt}^2}$$
$$【r>0だから】\Leftrightarrow r=\frac{(1+y’\hspace{1pt}^2)^{\large{\frac{3}{2}}}}{|y’\hspace{1pt}’|}$$
【途中の箇所では、分子の因数分解をすると結果的に3乗の形になっているという事です。】
◆曲率円の中心座標は確定しており、曲線も具体的に1つ決まっているとすれば、
中心から接点までの距離もただ1つに確定するわけです。
得られたこれらの式のy、y’、y” の所にf(c)、f'(c)、f”(c) を代入すれば公式の形になります。
簡単な例としては、2次関数y=x2とその1階微分と2階微分y’=2x、y’=2を考えてみて、
x=0でそれらの値はそれぞれ0、0、2ですから公式に当てはめると曲率円の中心は(0,1/2)で曲率半径は1/2になります。
曲線の「曲率」と公式
さて、曲率半径rの逆数、つまり1/rの事を曲線のある点での「曲率」と呼びます。
なぜわざわざ逆数を考えるのかというと、次の公式が成立し、平面での図形的な意味も持つためです。
平面上の曲線のある点での「曲率」とは曲率半径の逆数であると定義します。
$$(ある点での曲線の)曲率:k=\frac{1}{r}\hspace{5pt}と定義$$
曲線上の点が、ある定点から測った弧長sの関数であるベクトル \(\overrightarrow{X}(s)\) として表されるとして、
その点での曲線の長さ1の接線ベクトル\(\overrightarrow{T}(s)\)(微分はsで行う)と
x軸の正方向との成す角をsの関数としてθ=θ(s)とすると、
曲率との間に成立する次の関係式が成立します。
$$\left|\frac{d\overrightarrow{T}}{ds}\right|=\left|\frac{d\theta}{ds}\right|=k\hspace{5pt}\left(=\frac{1}{r}\right)$$
|dθ/ds|という導関数は、図形的に考えると曲線の「曲がり具合」を表す量になります。
接線ベクトルの導関数も同じく曲がり具合の度合いを表すと考えられますが、それは|dθ/ds|に実は等しくなります。
それが曲率半径の逆数に等しいという事については、逆三角関数を利用して証明します。
◆ベクトルの微分については、ベクトルの各成分を同じ変数で微分したものと定義されます。
証明(前半)
まず次式から証明します。
$$\left|\frac{d\overrightarrow{T}}{ds}\right|=\left|\frac{d\theta}{ds}\right|$$
証明方法の1つは、図形的な考察をしてから
「角度θが小さい時には sinθ≒θ」という近似式が成立する事を使うものです。
◆この近似式は、次の正弦関数に関する極限の変形として考える事ができます。$$\lim_{\theta\to 0}\frac{\sin \theta}{\theta}=1 により、\theta が0に近い時は\sin \theta≒\theta$$あるいは、マクローリン展開で第2項以降の3次以上の項を0に近似するか、正弦関数のθ=0での微分係数が1になる事からθ=0での近似一次式としてy≒θと考える事もできます。
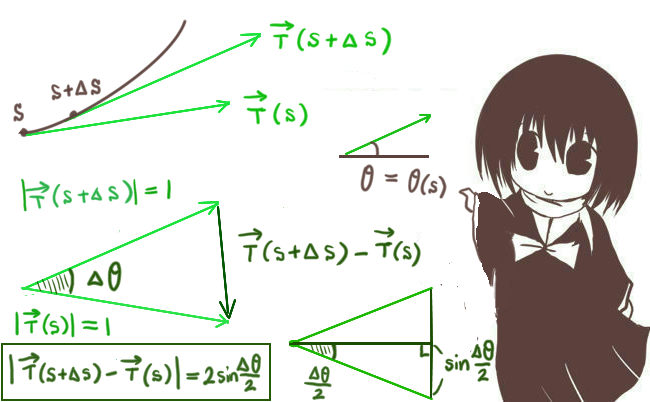
曲線の接線ベクトルは、大きさについては1に揃えるものを考えても角度には影響しません。そこで、曲線上の任意の点において接線ベクトルは長さ1であるとします。
すると、接線ベクトルを\(\overrightarrow{T}(s)\) とした時、\(\overrightarrow{T}(s+\Delta s)-\overrightarrow{T}(s)\) というベクトルを考えた時に、これは二等辺三角形の底辺になっています。【2辺の長さが1で、それらのはさむ角度がθ】
すると、その底辺の長さ |\(\overrightarrow{T}(s+\Delta s)-\overrightarrow{T}(s)\)| は実は簡単な図形的な考察からθで表す事ができます。
それは余弦定理で表す事もできますが、もっと単純に直角三角形の辺の比から正弦で表す事もできます。
結果は2sin(Δθ/2)になります。【長さ1の斜辺の正弦sin(Δθ/2)の2個分を考えただけです。】
$$|\overrightarrow{T}(s+\Delta s)-\overrightarrow{T}(s)|=2\left|\sin\frac{\Delta\theta}{2}\right|$$
【左辺が絶対値(プラスの値)なので、右辺にも絶対値をつけてあります。】
今、s→0の時にΔθ→0なので、sin(Δθ/2)≒Δθ/2となります。
$$|\overrightarrow{T}(s+\Delta s)-\overrightarrow{T}(s)|=2\left|\sin\frac{\Delta\theta}{2}\right|≒2\left|\frac{\Delta\theta}{2}\right|=|\Delta\theta|$$
$$\Leftrightarrow \frac{|\overrightarrow{T}(s+\Delta s)-\overrightarrow{T}(s)|}{\Delta s}≒\frac{\Delta\theta}{\Delta s}$$
$$\Delta s\to 0 の極限を取る事で【その時\Delta\theta \to 0】\left|\frac{d\overrightarrow{T}}{ds}\right|=\frac{d\theta}{ds}$$
証明(後半)
次に次式を証明します。
$$\left|\frac{d\theta}{ds}\right|=\frac{1}{r}$$
証明には逆三角関数とその微分を使います。
変数がxである状況に一度戻ると、導関数は接線の傾きを表すので、
その傾きは正接を使って tan θ = y’ と書けます。
これの逆関数を考えると、θ = arctan y’ と表記できます。
【これらは両辺ともにxの関数であるとします。】
すると、これをさらにxで微分すると次式になります。
$$\frac{d\theta}{dx}=\frac{y’\hspace{1pt}’}{1+y’\hspace{1pt}^2}$$
【逆三角関数の微分公式と、合成関数の微分公式を使用。(d/dx)arctan x=1/(1+x2)】
他方で、弧長を積分で表す公式を使うと【三平方の定理を利用した公式】次のように書けます。
$$s=\int_a^x\sqrt{1+y’\hspace{1pt}^2}dt$$
【積分の中身のy’ は形式上tの関数として書かれています。また、aはs=0となる点のx座標であるとします。】
このsをxで微分すると、微積分学の基本定理により次式になります。
$$\frac{ds}{dx}=\sqrt{1+y’\hspace{1pt}^2}$$
ここで、dx/dsを逆関数の微分公式により次のように表せます。
$$\frac{dx}{ds}=\frac{1}{\sqrt{1+y’\hspace{1pt}^2}}$$
ここで合成関数の微分公式を再び考えるとdθ/ds=(dθ/dx)(dx/ds) ですから、得られた関係式を組み合わせると次のように表せます。
$$\frac{d\theta}{ds}=\frac{d\theta}{dx}\cdot\frac{dx}{ds}=\frac{y’\hspace{1pt}’}{1+y’^2}\cdot\frac{1}{\sqrt{1+y’\hspace{1pt}^2}}=\frac{y’\hspace{1pt}’}{(1+y’\hspace{1pt}^2)^{\large{\frac{3}{2}}}}$$
ところで、前述の曲率半径は y’ 等の導関数の形で書くと次のようになります。
$$r=\frac{(1+y’\hspace{1pt}^2)^{\large{\frac{3}{2}}}}{|y’\hspace{1pt}’|}$$
つまり、絶対値記号さえつければ、dθ/dxとは丁度逆数の関係になっています。
$$よって、\left|\frac{d\theta}{ds}\right|=\frac{1}{r}が成立します。【証明終り】$$
曲率・接線・法線の関係(フルネー・セレーの公式)
さて、長さ1の接線ベクトル\(\overrightarrow{T}(s)\)を考える曲線上の点において、長さ1の法線ベクトル\(\overrightarrow{N}(s)\)も同時に考えてみます。(「法線」とはある点で接線に垂直である直線や線分の事。)
前述の曲率k(=1/r)を使うと、接線ベクトルと法線ベクトルとの間に次の関係が成立します。
長さ1の接線ベクトル\(\overrightarrow{T}(s)\)、長さ1の法線ベクトル\(\overrightarrow{N}(s)\)、曲率k(=1/r)の間には
次の2式の関係があります。
$$\frac{d\overrightarrow{T}}{ds}=k\overrightarrow{N},\hspace{15pt}\frac{d\overrightarrow{N}}{ds}=-k\overrightarrow{T}$$
この内容の意味を考えてみると、曲率はただのスカラー値(あるいはスカラー関数)ですから、「接線ベクトルのsによる微分」は法線ベクトルに平行であり、「法線ベクトルのsによる微分」は接線ベクトルに平行であるという事を意味します。
証明(第1式)
では、本当にそうなるのかという話です。
これを見るには、「接線ベクトル同士の内積」を微分してみると上手くいきます。
同じベクトルの内積は、単にそのベクトルの大きさの2乗であって、しかもここでは |\(\overrightarrow{T}(s)\)| =1として考えていますから、同じ接線ベクトル同士で内積を考えると次式です。
$$\overrightarrow{T}\cdot\overrightarrow{T}=1$$
これをsで微分してみますと、積の微分公式を成分ごとに適用すればスカラー関数同士の積の微分同様の関係になります。右辺は定数ですから微分すれば0です。
$$\frac{d\overrightarrow{T}}{ds}\cdot\overrightarrow{T}+\overrightarrow{T}\cdot\frac{d\overrightarrow{T}}{ds}=0\Leftrightarrow 2\frac{d\overrightarrow{T}}{ds}\cdot\overrightarrow{T}=0 \Leftrightarrow \frac{d\overrightarrow{T}}{ds}\cdot\overrightarrow{T}=0$$
【内積は可換(\(\overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{a}\))であるためにこうできる事に一応注意。】
$$という事は、2つのベクトル\frac{d\overrightarrow{T}}{ds}と\overrightarrow{T}は互いに垂直であるという事です。$$
そして、\(\overrightarrow{T}\)に垂直な長さ1のベクトルとして\(\overrightarrow{N}\)を考えていたわけですから、\(d\overrightarrow{T}/ds\) と \(\overrightarrow{N}\) は平行であって大きさだけが異なります。
しかし、上述の曲率kに関する公式から$$\left|\frac{d\overrightarrow{T}}{ds}\right|=k であったわけです。$$
$$という事は、\frac{d\overrightarrow{T}}{ds}=\left|\frac{d\overrightarrow{T}}{ds}\right|\overrightarrow{N}=k\overrightarrow{N}$$
【\(|\overrightarrow{N}|=1\) であるのでこう書ける事に注意。】
つまり、フルネー・セレーの公式の最初のほうの式が成立するという事です。【証明終り】
証明(第2式)
続いて、フルネー・セレーの公式の2番目のほうの式の証明です。
今度は\(\overrightarrow{N}\)について内積を微分してみると同様に次式になります。
$$\frac{d\overrightarrow{N}}{ds}\cdot\overrightarrow{N}=0$$
この式に、\(k\overrightarrow{T}\cdot\overrightarrow{N}=0\)を加えます。(ここでスカラーである曲率kはオマケとして、証明のために敢えてくっつけています。kがなくてもこの内積の関係は成立します。)
$$k\overrightarrow{N}\cdot\overrightarrow{T}+\frac{d\overrightarrow{N}}{ds}\cdot\overrightarrow{N}=\Leftrightarrow \left(k\overrightarrow{T}+\frac{d\overrightarrow{N}}{ds}\right)\cdot\overrightarrow{N}=0$$
ここで出てきた\(k\overrightarrow{T}+\large{\frac{d\overrightarrow{N}}{ds}}\)というベクトルもまた、法線ベクトルに垂直(従って接線ベクトルに平行)という事になります。他方で、このベクトルは別の式からも出てきます。
それは\(\overrightarrow{T}\cdot\overrightarrow{N}=0\)を微分する事によって出てきます。
$$\frac{d\overrightarrow{T}}{ds}\cdot\overrightarrow{N}+\frac{d\overrightarrow{N}}{ds}\cdot\overrightarrow{T}=0\Leftrightarrow (k\overrightarrow{N})\cdot\overrightarrow{N}+\frac{d\overrightarrow{N}}{ds}\cdot\overrightarrow{T}=0$$
$$\Leftrightarrow k+\frac{d\overrightarrow{N}}{ds}\cdot\overrightarrow{T}=0\Leftrightarrow (k\overrightarrow{T})\cdot\overrightarrow{T}+\frac{d\overrightarrow{N}}{ds}\cdot\overrightarrow{T}=0$$
$$\Leftrightarrow \left(k\overrightarrow{T}+\frac{\overrightarrow{N}}{ds}\right)\cdot\overrightarrow{T}=0$$
【既に得られている関係の代入と、\(\overrightarrow{N}\cdot\overrightarrow{N}=\overrightarrow{T}\cdot\overrightarrow{T}=1\)を利用した細工を行っています。】
という事は、\(k\overrightarrow{T}+\large{\frac{d\overrightarrow{N}}{ds}}\)というベクトルは接線ベクトルにも垂直である事になります。これは、法線ベクトルにも接線ベクトルにも垂直である事を意味しますが、平面上でそのようなベクトルはゼロベクトルしかありませんから、次のようになります。
$$k\overrightarrow{T}+\frac{d\overrightarrow{N}}{ds}=0\Leftrightarrow \frac{d\overrightarrow{N}}{ds}=-k\overrightarrow{T}$$
これはフルネー・セレーの公式の2番目のほうの式になっています。【証明終り】