高校数学での、直交座標上での図形的な性質と関連させた2次関数の式、および問題を解くコツについて説明します。
およそ、センター試験の出題範囲レベルに対応できる程度の問題について解説します。
2次関数と放物線の関係
■ 2次関数を表す図形と高校数学での考察点
■ 2次関数の「頂点」
■ 参考:頂点を調べる別の方法・・2次方程式の解、微分
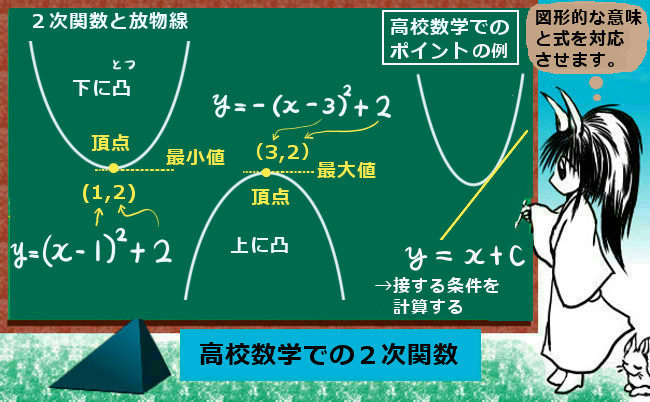
2次関数を表す図形と高校数学での考察点
2次関数自体は中学校でも教わるかと思いますが、高校数学だとより自由自在に平面の中での図形的な考察を、式によって(手計算で)進める事が行われます。
2次関数が直交座標上で表す形は「放物線」です。最大値と最小値のどちらか1つを必ず持ち、x軸の無限遠方では必ず+側に無限大になるか-無限大になるのかのどちらかになります。
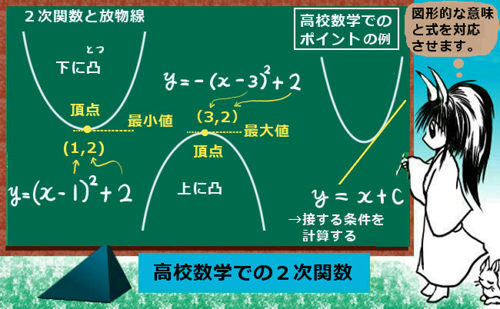
$$2次関数\hspace{5pt}Ax^2+Bx+C\hspace{5pt}が表す図形:「放物線」$$
この式で、Aの値がプラスであれば「下に凸【とつ】」の形、逆にAがマイナスであれば逆さまの「上に凸」の形になります。
尚、A=0であれば1次関数になってしまうので、その場合に限っては図形は放物線にならず直線になります。
このように、式の中での性質や特徴が、図形的にはどのような意味を持つのかを理解しておく事が問題を解くうえでのポイントになります。
2次関数の「頂点」
2次関数が、直交座標上でどのような場所にあるかを見るには、「頂点」の位置を調べます。
そのために、2次の項と1次の項を2乗の形に変形します。
★尚これは2次関数であるから必ず、しかも簡単にできる操作で、3次式以上だと一般的にはそううまくはいきません。3次式の場合は高校数学の手計算では多くの場合、微分を用いて調べます。簡単に後述しますように、2次関数でも微分の手法を使う事は可能です。
例えば次のような具体的な2次関数については次のようになります。
$$x^2+4x-6=(x+2)^2-4-6=(x+2)^2-10$$
この時関数はx=-2を代入すると最小値-10を持ちます。これは最後の式にそれを代入して直ちに最小値を得るのですが、間違いのないようにもとの式に代入してみるのもよいでしょう。
(-2)・(-2)+4・(-2)-6=4-8-6=-10ですから確かに合っています。
この時、2次関数が最小値をとる座標である(-2,-10)をこの2次関数の「頂点」と呼ぶのです。
2次の項がマイナスでも同じ操作をします。
$$-x^2+4x-5=-(x-2)^2+4-5=-(x-2)^2-1$$
この時は、2次関数はx=2で最大値-1を取ります。この最大値をとる座標(2,-1)がこの2次関数の「頂点」です。
関数の中の係数が未知数である場合も同様です。
$$x^2+(A-2)x+1=\left(x+\frac{A-2}{2}\right)^2-\frac{(A-2)^2}{4}+1=\left(x+\frac{A-2}{2}\right)^2-\frac{A^2-4A+4}{4}+1$$
$$=\left(x+\frac{A-2}{2}\right)^2-\frac{A^2}{4}+A$$
この例の場合、最小値の値もAに関する「2次式」ですから、問題の形式によってはさらに計算が続きます。高校数学だと、この手のタイプの問題のほうが問われやすいかもしれません。応用問題についても後述しているので必要に応じて参照してください。
参考:頂点を調べる別の方法・・2次方程式の解、微分
2次関数で、x軸との交点が2つある場合に限って言えば、x軸との2交点の中点のx座標が頂点のx座標に等しくなります。そのため、ものによっては、2交点を先に出してしまって中点を考えて頂点を出す事もできます。例えば次のような感じです。
$$x^2+2x=x(x+2)より、x=0,-2でx軸(y=0直線)と交わる。よって、頂点のx座標は-1$$
解けるなら何の手法を使ってもよいのですが、複数の手法を知っているとチェックとして使えるでしょう。
参考までに、2次関数の頂点の位置を調べるには、微分を使う事もできます。センター試験では微分を使わなくても問題を解けるように必ず作ってあるので微分を使う必要はないですが、解答が合っているかどうかのチェックなどに使う事ができます。
上記の例だと例えば次のようになります。
$$(x^2+4x-6)^{\prime}=2x+4$$
$$(-x^2+4x-5)^{\prime}=-2x+4$$
$$\{x^2+(A-2)x+1\}^{\prime}=2x+A-2$$
$$(x^2+2x)^{\prime}=2x+2$$
これらの「導関数」が0になる値が、2次関数の場合では最大値あるいは最小値をとるxの値、すなわち放物線の頂点のx座標になります。(他の関数の場合には直ちに最大または最小となる値とは言えないので注意。)
本質的には、2次関数の頂点は手計算では平方完成によっても微分によっても、本来はどちらの方法でも調べる事ができるのです。
2次関数と放物線に関する応用問題
■ 2次関数の最大値・最小値に関連させた問題
■ 定義域が限定された場合の最大・最小
■ 直線と放物線の交点問題
■ 2つの放物線同士の交点
2次関数の最大値・最小値に関連させた問題
$$■問い:2次関数y= x^2-4x+5はx軸と何個の交点を持ちますか。$$
こういった問題の場合には、式変形して図形の様子を見て調べます。
$$x^2-4x+5=(x-2)^2+1$$
であり、最小値は1です。という事は、x軸(直線y=0)との交点は存在しません。交点の数は0個です。【解答】
こんな具合です。
ただし、大学入試等での問題では、こういったシンプルな問題はあまり出してくれません。もう少し計算の手順が必要な形で出題されると考えるべきでしょう。
例えば、2次関数の係数も未知数である場合には計算はさらに続き得ます。上記でも例に挙げた2次関数を使って見てみましょう。
$$■問い:2次関数y=x^2+(A-2)x+1はx軸と何個の交点を持ちますか。(Aは実数とします。)$$
$$x^2+(A-2)x+1=\left(x+\frac{A-2}{2}\right)^2-\frac{A^2}{4}+A$$
このように最小値自体がAの値によって変化し、しかもAに関する2次式ですので今度は2次方程式を解く作業になります。
$$-\frac{A^2}{4}+A=-A\left(\frac{A}{4}-1\right)$$
この場合はあっさり因数分解できるので、0と置いた時の解が分かります。A=0または4の場合に、「もとの2次関数の最小値」が0になるわけです。その時、もとの2次関数とx軸との交点は1つだけです。頂点がx軸に接する形になります。
また、0<A<4の時には「もとの2次関数の最小値」がプラスの値になってしまいますから、もとの2次関数とx軸の交点は存在しません。
A<0またはA>4の時には「もとの2次関数の最小値」はマイナスで、xの値を増やすあるいは減らす事で関数の値は大きくなっていきますからx軸と確実にぶつかります。ですからもとの2次関数とx軸との交点は2個です。
ですので、A<0またはA>4のとき交点は2個、A=0またはA=4のとき交点は1個、0<A<4のとき交点は0個という、場合分けを含んだ答えになります。【解答】
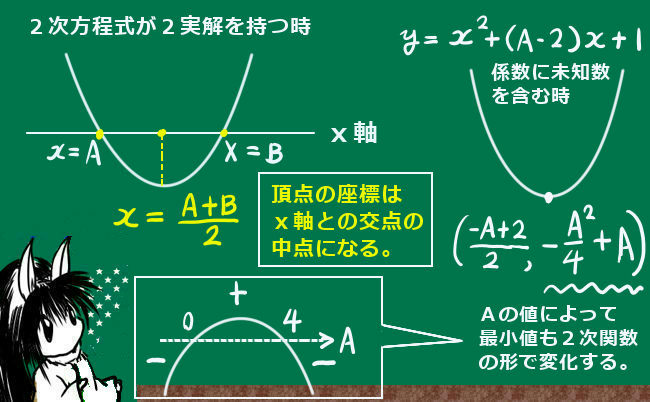 A<0またはA>0の時、最小値がマイナスの値になり、もとの2次関数は下に凸の形の放物線ですから必ずyの値が0になる点が2つ存在する、すなわちx軸と2点で交わるという事です。
A<0またはA>0の時、最小値がマイナスの値になり、もとの2次関数は下に凸の形の放物線ですから必ずyの値が0になる点が2つ存在する、すなわちx軸と2点で交わるという事です。この例での2次関数の場合、最小値がAに関する上に凸の2関数なので、「最小値が取り得る値の中にも最大値がある」という性質のものになります。具体的にはA=2の時に「最小値の」最大値が1になり、Aが全実数の中のどの値であってももとの2次関数の頂点に相当する最小値は1を超えない事を意味します。これは1次の項の係数が0の時です。
定義域が限定された場合の最大・最小
もう1つ重要な出題として、定義域(xの範囲)を限定した範囲での最大値や最小値を問うタイプのものがあります。
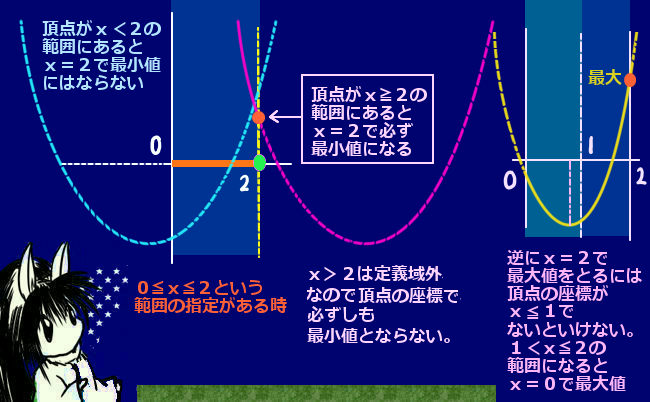
これはどういうものかというと、例えば下に凸である2次関数の最小値は通常は頂点のy座標ですが、そのx座標が定義域に含まれていない時には定義域の端点で最小値をとります。
■問い:0≦x≦2の範囲で、y=x2-2px+4について
①:x=2で最小値をとるためのpの範囲はどのようになりますか。
②:x=2で最大値をとるためのpの範囲はどのようになりますか。
この手の問題における2次関数の性質自体は正直、大学以降の数学であまり重要とは言えないと思いますが、2次関数のグラフの性質の理解度を問う出題という事でしょう。
まず、1次の項に未知の係数pがありますから頂点のx座標もy座標も変化するパターンです。
y=x2-2px+4=(x-p)2+4-p2
①:ここで、通常であればx=pで最小値をとるという事になりますが、「x=2で最小値をとる」という条件があり、さらに0≦x≦2というxの範囲の指定もあるのでp≧2であれば、常に対象の2次関数は定義域の端点であるx=2で最小値をとります。なのでp≧2です。【①の解答】
これは、式だけでは分かりにくいのでグラフを見ながら様子を把握したほうがよいでしょう。
②:次に所定の場所で最大値をとる場合です。通常であれば下に凸の2次関数は無限に大きくなるので最大値はそもそもありませんが、ここでは閉区間としてxの範囲が指定されているので最大値を持つという事です。
頂点の座標x=pが動き、定義域が閉区間[0,2]、x=2で最大値をとるという条件です。
この場合には、逆にp≦2であれば済む話かというとそうでない事が「ひっかけ」です。
頂点が閉区間[0,2]の中点よりも右半分側に来ると、今度は区間の反対側の端点であるx=0でyが最大値になってしまいます。頂点の座標がp=1の時にx=0,2の両方で最大値になります。つまり、x=2で最大値になるにはp≦1という事です。【②の解答】
このように、高校数学だと多少ひねりを入れた計算をさせる場合があります。やっている事自体は難しくないのですが、慣れていないと突然問われた時にとまどってしまうでしょう。
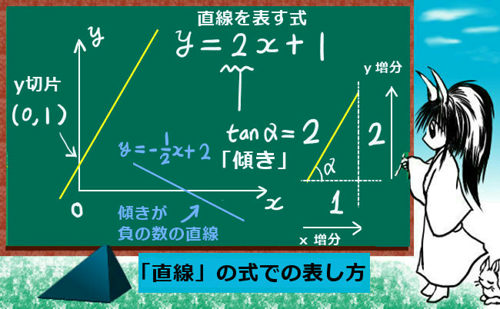
直線と放物線の交点問題
1次関数である直線と、2次関数である放物線の交点を計算させるような問題は、センター試験レベルだと問われる事があります。
考え方は難しくありません。
1次関数と2次関数を等号で結んで方程式を作り、2次方程式の解を出せばよいのです。
解が重解の場合には交点は1つだけで、直線は放物線の接線になります。また、解が複素数解になる場合には交点はないという事に対応します。
$$■問い:直線y=x+2と放物線y=x^2-x-3の交点はいくつありますか。$$
まず、等式で結びます。それから、解の様子が分かるように変形します。
$$x+2=x^2-x-3\Leftrightarrow x^2-2x-5=0$$
$$\Leftrightarrow (x-1)^2-1-5=0\Leftrightarrow (x-1)^2=6$$
のようになるので、これは異なる実数解を2つ持ちますね。したがって、交点は2つ存在します。【解答】
「2乗=正の数」となる事で異なる2つの実数解が存在する事が分かります。「2乗=0」であるなら重解を持ち、「2乗=負の数」であるなら2つの異なる複素数解です。
尚、本当に単に交点の数だけを問う問題であれば2つの図形のグラフを描いてみる事でも答えが分かる場合もあります。上記の例だと2点で交わるので、グラフを描く方法でも分かるでしょう。
ただし、その方法だと交点が1個だけで直線が放物線に「接する」時や、交点を持つのか持たないのか微妙な時の判定が難しい事に注意が必要です。
この手の問題も、式の中の係数に未知数を入れて、「2つの交点を持つ条件は何か」とか「直線が放物線に接するための条件を述べなさい」とか、そういった形でひねった出題がなされる事も多いと思います。やる事は基本的に同じです。
例えば、直線のy切片が変化し得る条件で、直線が放物線に接する条件を考えてみましょうか。
$$■問い:直線y=x+Cが放物線y=x^2-x-3に接するためのCの値は何ですか。$$
ここでもやる事は同じです。2式を等号で結びます。
$$x+C=x^2-x-3\Leftrightarrow x^2-2x-3-C=0$$
$$\Leftrightarrow (x-1)^2-4-C=0$$
ここで、4+C=0になれば重解を持ちますのでC=-4の時に直線は放物線に接します。【解答】
■参考:この問題に関しても、微分を使う事もできます。
$$(x^2-x-3)^{\prime}=2x-1$$
であり、この導関数の値が接線の傾きですから、
2x-1=1⇔x=1
これが、もとの2次関数に対して「傾きが1である接線」が接する点のx座標です。これを2次関数の式に代入するとy座標も得られます。
その点の座標は(1,-3)です。
y=x+Cがこの点を通るとすると、
-3=1+C⇔C=-4【解答】
さらに、x2-2x-3-C=0が重解を持つための条件を出す場合にも微分を使えます。左辺を関数とした時にx軸に接する、つまり極小値をとるy座標の値が0であるので、導関数2x-2=0としてx=1、その値を方程式に代入して1-2-3-C=0 ⇔ C=4ともできます。
これらの方法はセンター試験等では不要ですが(出題範囲外なので)、知っていると計算のチェック用に使える事もあります。
2つの放物線同士の交点
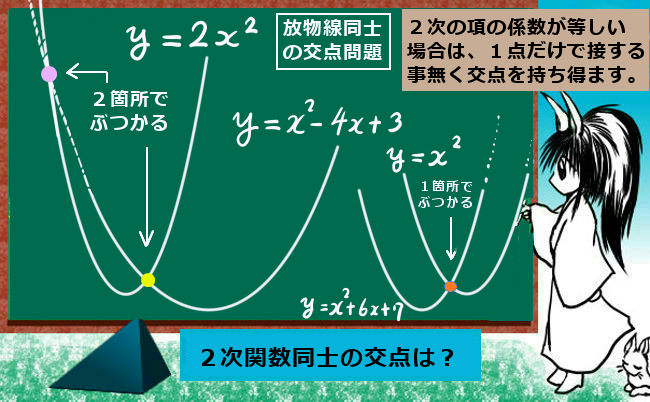
出題頻度は低いですが、あり得るパターンとして放物線同士の交点を考える問題もあります。
$$■問い:y=2x^2+2x+1とy=x^2-2x+Cが1点だけで交わるためのCの値は何ですか。$$
等号で2式を結びましょう。
$$2x^2+2x+1=x^2-2x+C\Leftrightarrow x^2+4x+1-C=0$$
$$\Leftrightarrow -(x+2)^2-3-C=0$$
これが重解を持つためにはC=-3です。【解答】
この場合には、1点だけで交わるには接するしかない事が、式からも分かります。仮に、1点で「突き破るように」交点を持った時、別のもう1点で必ず交わってしまうためです。
しかし、放物線同士の場合には、1点だけで「突き破るように」交点を持つ場合もあり得ます。それは、2次の項が等しい場合です。
$$y=x^2+2x+1, y=x^2+x$$
を等号で結んでみましょう。
$$x^2+2x+1=x^2+x\Leftrightarrow x+1=0$$
この場合にx=-1という解が得られますが、2次方程式の重解ではなくて1次方程式の解になっています。これが「突き破って」1点だけで交わっている交点であり、xの値をどれだけ増やしても減らしても、その先の別の点で交わる事はないという事です。
参考:放物線と円の交点の問題は?
また参考までに、放物線と円の交点を問う問題も高校数学の範囲で、一応あり得るものではあります。
$$放物線y=Ax^2+Bx+Cと円(x-S)^2+(y-T)^2=R^2$$
を考えるわけですが、放物線のyを円のほうの式に代入すると、一般的には4次方程式になってしまいます。
実際、円と放物線を考えると、4点や3点で交わる可能性がある事に対応しています。そのため手計算だと非常に複雑な計算になりがちで、出題する側も調整が面倒と思われるのであまり出ないと思います。
サイト内関連記事【高校数学で扱う関数】
★尚、大学入試では3次関数については、基本的に微積分(特に微分)での出題になります。