このページでは古典力学での「仕事」と、運動エネルギーとの関係について述べます。
数学的には、ベクトルの微積分の応用であり、ベクトルの内積の応用でもあります。
内積と「仕事」
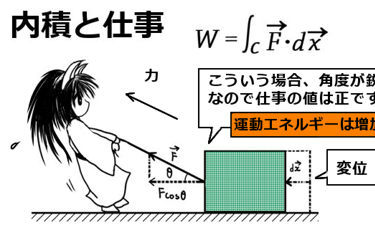
平面や空間での物体の運動を考える時、力のベクトルの向きと、現に運動している物体の運動の方向・・・つまり速度ベクトルの方向は、互いに異なるという事も普通にあります。
例えば、床に置かれた重い物に紐を付けて斜めに引っ張ったところ床に対して引きずるように水平に動いたとすれば、力ベクトルは斜め上方向、速度ベクトルは水平方向という事になります。
このような時に力ベクトルと速度ベクトルとの「内積」を考えます。
そしてそこから、「仕事」という量を積分を使って定義します。
☆詳しくは、ここで使う積分は接線線積分と呼ばれるものです。
\(\overrightarrow{F}\cdot \overrightarrow{dx}(または \overrightarrow{F}\cdot \overrightarrow{\Delta x})\) を、物理学では「仕事」と呼びます。
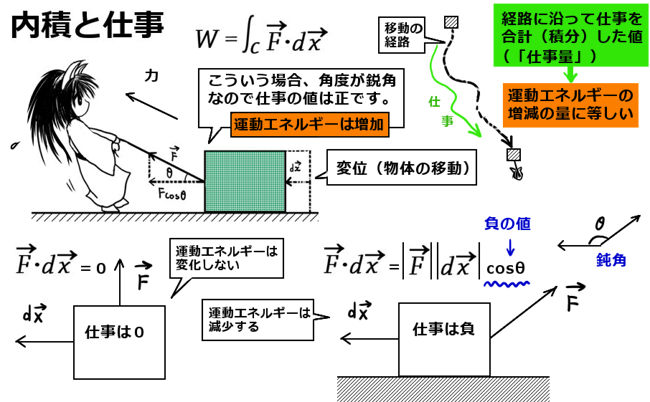
これを経路に沿って合計した量(積分値)を「仕事量」と呼ぶ事があります。
◆仕事はベクトルの内積ですので、
\(\overrightarrow{F}\cdot \overrightarrow{dx}=|\overrightarrow{F}|\hspace{2pt} |\overrightarrow{dx}|\cos\theta\) のようにも書く事ができます。
マイナスの値になる事もあり、その場合にも物理的な意味を持ち、角度とその余弦も力と物体の運動に対応したものになります。
この「仕事」を考える事により、じつは「『力』と『物体の運動』と『エネルギー』」を数式的に関連付ける事ができるのです。
運動方程式が成立しているとすれば、その事は数学的に導出できます。結論の関係式は次のようになります。
関係式は次のようなものです。
$$\int_{t_1}^{t_2}\overrightarrow{F}\cdot \frac{d\overrightarrow{x}}{dt}dt=\frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2$$
左辺の積分は仕事量、右辺は時間の区間の始まりと終わりでの運動エネルギーの差です。
左辺と右辺とで物理学的な単位は等しく、ともに[J](ジュール)です。
意味としては、なされた「仕事」の量と運動エネルギーの増減の量は等しいという事です。
この関係式の数学的な導出には、微分の基本公式とベクトルの微積分が直接的に関係しています。
仕事と運動エネルギーの関係式の導出
まず運動方程式をベクトルの形で書いて、両辺に対して速度ベクトルとの内積を考えます。
$$【運動方程式】 \overrightarrow {F}=m\frac{d^2\overrightarrow{x}}{dt^2} $$ $$【速度ベクトルとの内積】 \overrightarrow {F}\cdot \frac{d\overrightarrow{x}}{dt}=m\frac{d^2\overrightarrow{x}}{dt^2}\cdot \frac{d\overrightarrow{x}}{dt}$$
運動方程式の加速度を含む側について、加速度は位置座標を表すベクトルの時間による2階微分である事に注意します。この部分と、速度ベクトルの内積を考えると、「2階微分と1階微分の積」という、一見わけの分からないものが出てきます。これは一体何でしょう?
それについての数式的な解釈は次のように行います。
合成関数に対する微分公式を用いると、「関数の2乗」を微分すると1階微分が積の形でくっついてくる事が分かります。
すると、「1階微分の2乗」を(1回)微分すると、 「2階微分と1階微分の積」 が出てくるのです。この時、2という係数も出てきますから1/2を乗じて係数調整を行います。
計算を進めると、じつは次のように変形できます。
$$ \overrightarrow {F}\cdot \frac{d\overrightarrow{x}}{dt}=\frac{d}{dt}\frac{m}{2}\left|\frac{d\overrightarrow{x}}{dt} \right|^2$$
具体的な数式を見てみましょう。
まず、ベクトルではなくてtを変数とする1変数関数x=x(t) について考えてみます。
$$\frac{dx}{dt}\frac{d^2x}{dt^2} などは、異なる導関数同士の「積」です。$$
$$\frac{d}{dt}\left\{\frac{m}{2}\left(\frac{dx}{dt}\right)^2\right\}=2\cdot\frac{m}{2}\frac{dx}{dt}\frac{d^2x}{dt^2}=m\frac{dx}{dt}\frac{d^2x}{dt^2}$$
2乗の部分の微分については、合成関数の微分公式を使っています。
質量mは定数扱いです。
これがベクトルの各成分\(x_1, x_2, x_3\) (それぞれ時間tの関数)について言えます。
そこで、次のように内積を考えるのです。
$$m\frac{d^2\overrightarrow{x}}{dt^2}\cdot \frac{d\overrightarrow{x}}{dt}=m\frac{dx}{dt}\frac{d^2x_1}{dt^2}+m\frac{dx}{dt}\frac{d^2x_2}{dt^2}+m\frac{dx}{dt}\frac{d^2x_3}{dt^2}$$
$$=\frac{d}{dt}\frac{m}{2}\left(\frac{dx_1}{dt}\right)^2+\frac{d}{dt}\frac{m}{2}\left(\frac{dx_2}{dt}\right)^2+\frac{d}{dt}\frac{m}{2}\left(\frac{dx_3}{dt}\right)^2$$
$$=\frac{d}{dt}\frac{m}{2}\left\{ \left(\frac{dx_1}{dt}\right)^2+\left(\frac{dx_2}{dt}\right)^2+\left(\frac{dx_3}{dt}\right)^2 \right\}
$$
$$=\frac{d}{dt}\frac{m}{2}\left|\frac{d\overrightarrow{x}}{dt} \right|^2$$
最後のところは、$$\frac{d\overrightarrow{x}}{dt}=\left(\frac{dx_1}{dt},\frac{dx_2}{dt},\frac{dx_3}{dt} \right) というベクトルの「大きさの2乗」$$を考えているのです。物理的な意味としては、これは物体の速度ベクトルの大きさの2乗、つまり「速さ」の2乗を意味します。内積の計算によって各成分を含む項の和が出てきて、うまい具合に「速さ」になっている事に注意してみてください。
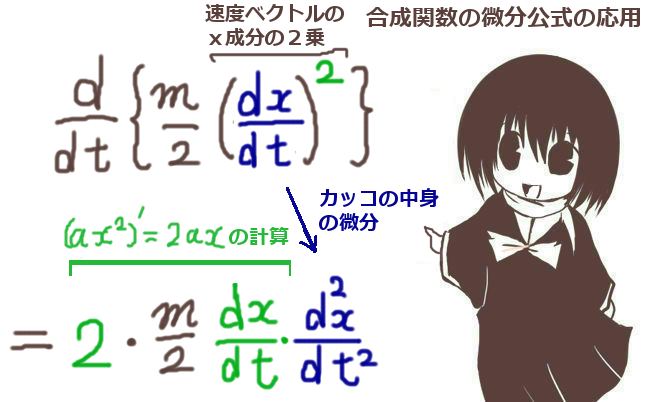
「速度ベクトルのx成分の2乗」の2倍と、「加速度ベクトルのx成分」との積になります。
数学の合成関数の微分公式を使用しています。
変形して得られた式の両辺をてきとうな時間 \(t_1,t_2\) で定積分したものを考える事で、仕事量と運動エネルギーの関係式が得られます。
$$\int_{t_1}^{t_2}\overrightarrow {F}\cdot \frac{d\overrightarrow{x}}{dt}dt= \int_{t_1}^{t_2}\frac{d}{dt}\frac{m}{2}\left|\frac{d\overrightarrow{x}}{dt} \right|^2dt= \frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2$$
「運動エネルギー」は次式で定義します。記号は、Tを使う事が多いです。
$$T=\frac{1}{2}mv^2\left(=\frac{m}{2}\left|\frac{d\overrightarrow{x}}{dt} \right|^2\right)$$
この量は正の仕事がなされれば増加し、負の仕事がなされれば減少します。また、仕事がなされなければ運動エネルギーは変化しない、という事も意味します。
(※数学的な定義においても内積は正の値だけでなくゼロや負の値も取り得るものであり、図形的な意味も持つわけです。)
この運動エネルギーに加えて、さらに「位置エネルギー」というものを考え、両者の和を「力学的エネルギー」と呼びます。重力等の「保存力」のみが働いている場合、力学的エネルギーの保存則が成立します。
また、実験・観測から定量的(※)な意味でのエネルギーの等価性が確認されています。運動エネルギーは量としては熱エネルギーや電気エネルギーに変換されると見なす事ができて、物理学だけでなく種々の工学等での理論計算に用いられています。
(※)「定量的に」と言うのは、例えば「力学的エネルギーの『入力』が電気エネルギーと熱エネルギーの『出力』に等しい」といった計算ができるという意味になります。発生する熱エネルギーに関しては、望んでいるものでなければ「損失」と呼ぶ事も多いです。
熱なども含めて考えると、一般的にエネルギー全体についての保存則が成立します。
例えば摩擦によって物体が停止すれば当然ですが運動エネルギーはゼロになりますが、この時にエネルギーの量自体はどこかに消えたというよりは、同じ量の熱エネルギーに変換されたと考えて考察が行われます。
■関連コンテンツ(サイト内リンク)
- ベクトルと内積【基本事項】
- 古典力学とベクトルの微積分
- 位置エネルギーと保存力
- 合成関数に対する微分公式
- 三角比および三角関数【余弦cosθについての説明】
- 初等関数の微分公式集【微分の基本事項】
- 積分の考え方と基本計算【定積分についての初歩的な内容】