重積分の定義と計算法、累次積分、変数変換と関数行列式について説明します。
微積分の中では、微分方程式・無限級数・偏微分の理論と並んで、応用数学でも重要です。
高校数学での1変数の積分の定義と公式は別途に詳しく説明しています。
重積分の物理学での応用としては、例えば電磁気学等で使うガウスの発散定理があります。
重積分とは「多変数関数に対する積分」
重積分とは、多変数関数に対する積分です。定積分・不定積分の両方があります。2変数の時を2重積分、3変数の時を3重積分、n変数の時をn重積分(あるいは「多重積分」)・・と、言う事もあります。
■ 重積分の定義と表記方法
■ 積分領域が長方形ではない場合の考え方と処理
■ 重積分の簡単な計算:累次積分による例
■ 重積分と面積・体積との関係
重積分の定義と表記方法
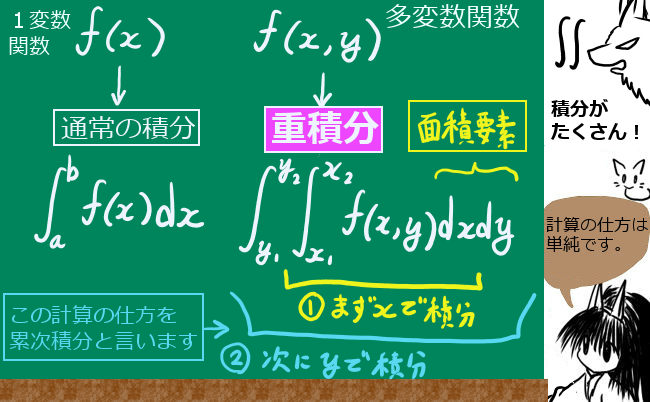
多変数関数F(x,y,z,・・)をx、y、z、・・のそれぞれで積分する計算を重積分と言います。
単純化のため、ここでは2変数関数F(x,y) を例にします。
計算の仕方の結論を先に言ってしまいますと、まずxだけで積分の計算を行い、その後でyについて積分の計算を行います。yの積分を先に行ってからxで積分しても同じ結果になります。
- まず最初は、yなどの変数は定数とみなしてxで積分計算。
- xに関して定積分の値を代入したら、今度はyで積分計算。
このような計算の仕方を「累次積分」とも言います。
xの次にyと、続けて逐次的に計算するという意味合いです。
1つの積分変数に着目して積分計算する時は、他の変数は定数扱いにします。
不定積分として表記するなら次のような形になります。
変数を増やした場合でも表記方法は2変数の場合に準じます。
例えば3変数なら次のようになります。
$$ 定積分:\int_{z1}^{z2} \int_{y1}^{y2}\int_{x1}^{x2}F(x,y,z)dxdydz \hspace{10pt}不定積分\int \int\int F(x,y,z)dxdydz$$
積分領域が長方形ではない場合の考え方と処理
◆積分区間について、積分を行うxy平面の領域が「長方形」であれば積分区間は
定数を端とする閉区間になります。(例えば [0,1])
他方、領域が座標軸に対して斜めになっていたり、曲がっていたりする場合には次のようにします。
まず、いずれかの変数をもう1つの変数の関数として表して、それを区間とします。
つまり、xとyの2変数で重積分をする時に、まずxで積分をするとすれば領域の端を構成する曲線をyの関数x1=x1(y)、x2=x2(y)として区間としておきます。
次に、yを定数とみなして原始関数を式で表せたとします。
その式のxの部分に、通常の定積分計算のようにx=x2(y)とx=x1(y)を代入をして引き算します。
【例えばx=2yであるとかx=y2であるといった形を直接代入します。】
その計算の結果、変数xは全て消えてyだけの関数になります。
最後に残った変数については、定数の区間の定積分を実行します。
3変数以上の場合でも考え方は同じで、変数をx、y、zとして積分する場合には、最初に積分をする変数の区間は2変数関数として表され、2番目に積分する変数は区間が1変数関数で表され、最後に残った変数は区間が定数という形になります。
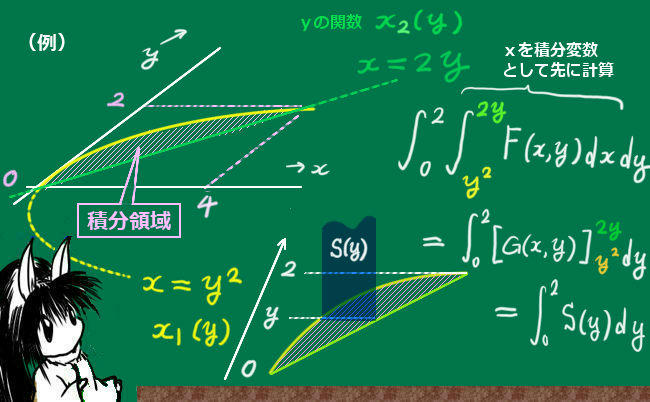
例えば、x=y2とx=2yで囲まれる領域を積分範囲を考えたとしましょう。この時に、yに関しては閉区間 [0,2]を考えるとします。その領域上でてきとうな2変数関数F(x,y)があったとして、まずxで積分をする前提であるなら重積分は次のように計算します。
$$\int_{y1}^{y2}\int_{x1}^{x2}F(x,y)dxdy=\int_0^2\int_{\large{y^2}}^{\large{2y}}F(x,y)dxdy$$
一度そのように具体的な関数を区間に代入して表した場合には、積分の順番はx→yのようにきちんと決めて計算を行います。
$$つまり、\int_0^2\left(\int_{\large{y^2}}^{\large{2y}}F(x,y)dx\right)dyのような形で計算を行います。$$
重積分の簡単な計算:累次積分による例
もう少し簡単な例として、てきとうな2変数関数としてF(x, y) = xy というものを考えて、重積分してみましょう。
この時、定積分の場合は x の範囲と y の範囲の両方が指定される必要があります。ここでは、例として x の積分区間は [0, 1]、y の積分区間は [4, 5] という範囲であるとします。【つまり積分する領域が長方形である場合です。】
【★数学では、この2つの範囲を表記する為に [0, 1] × [4, 5] と書く場合があります。この場合の「×」記号は、掛け算ではなくて「直積集合」を表すための記号です。】
では、その設定で重積分してみます。
$$ \int_{4}^{5}\int_{0}^{1} F(x, y) dxdy= \int_{4}^{5}\int_{1}^{2} xy dxdy = \int_{4}^{5} \left[\frac{yx^2}{2}\right]_0^1dy= \int_{4}^{5} \frac{y}{2}dy=\left[\frac{y^2}{4}\right]_4^5=\frac{9}{4} $$
まずyを定数とみなして計算を進める事がポイントです。
1変数の積分の計算さえできれば、計算の考え方としては難しくないはずです。
重積分と面積・体積との関係
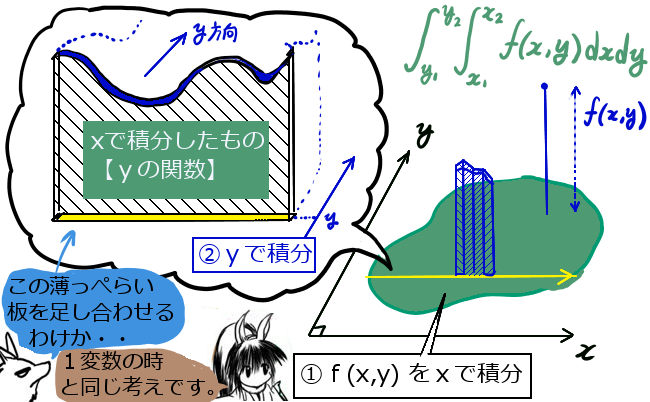
1変数の関数の積分には、グラフで表した関数の「面積」という意味がありました。
では多変数の重積分には何の意味があるかというと、2変数関数の重積分には「体積」としての意味があります。この時、積分変数の側のdxdyを面積要素と呼ぶ事があり、物理などで用いる場合はdSと書く場合もあります。(S は surface の頭文字です。)
◆参考:ベクトル解析における法線面積分の考え方
xとyが直交座標の変数であるとき、dxdyは(微小な)長方形の面積というわけです。累次積分によって重積分を計算する場合は、1回目にxで積分することで、各dyに対する非常に薄い板のような立体ができあがり、それをyで積分して全体の体積になるというイメージです。
他方、3変数関数の重積分の場合は、空間上に分布する何らかの値を、特定の領域全体に渡って合計したものという意味があります。この場合、dxdydzを体積要素と呼ぶ事があり、物理などではdvで表記する事もあります。(vは volume の頭文字。)
1変数の積分にも言える事ですが、多変数の重積分においても、不定積分がうまく導出できない場合があります。しかし、積分は「和」の極限値であり、近似できるという考え方によって、コンピュータ(プログラミング)による「数値計算」で積分値を計算する事が可能です。
変数が増えても、物理的な意味付けができる場合には dX1dX2dX3dX4・・・といった積分変数の積を考えて重積分を行う場合もあります。
重積分の変数変換論
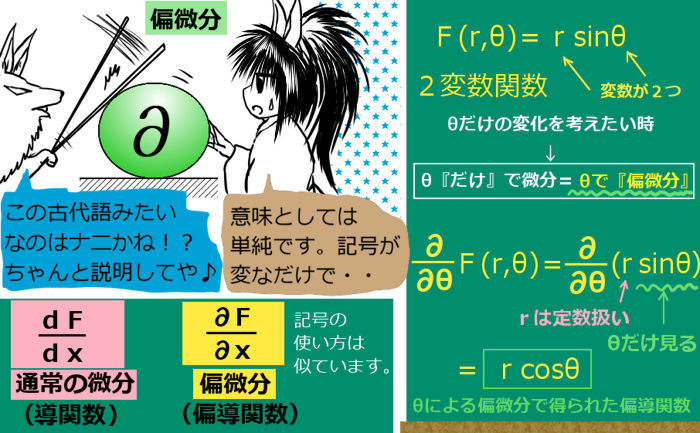
重積分の積分変数の変換は、偏微分の理論と深い関係があります。
■ 変数変換の公式と、基本的な考え方:曲線に沿った積分
■ 変数変換の理論と関数行列式:2変数の場合
■ 3変数以上の場合の重積分の変数変換
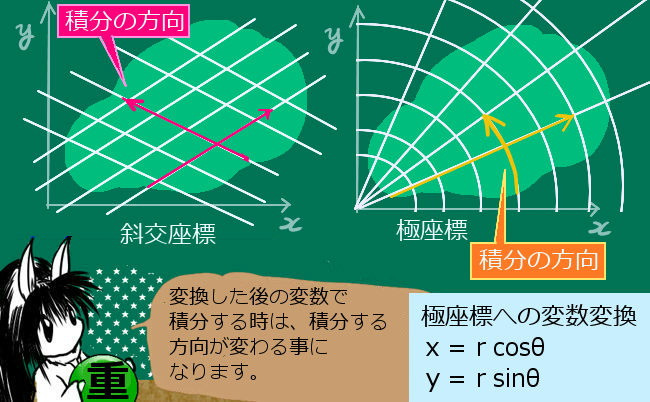
変数変換の公式と、基本的な考え方:曲線に沿った積分
通常の重積分を累次積分で計算する時には、まずx軸に沿って関数の積分値を、各yの値に対して計算し、次にy軸に沿って積分をするわけです。
そこで、x=2u+v, y= u+3v のような変数変換をするとします。この時、xとyではなくてuとvで積分する事を考えてみます。
この場合、 じつはxy平面上の「u曲線」と「v曲線」に沿って積分を行う事になります。上記のように変数変換がuとvの1次式である場合は曲線ではなく直線になりますから斜交座標のようなります。
物理などで使われる変換の代表的なものは、極座標変換です。この場合、x=rcosθ, y=rsinθ という変換を行いますが、rとθで積分をする場合には θ 曲線(rが一定:つまり同心円)とr曲線(θが一定:つまり原点から伸びる放射状の直線)に沿って重積分を行うというわけです。
ただし、変換の式を直接代入するだけではじつは不十分で、次に述べますように「関数行列式」と呼ばれるものを掛け算しないと、計算がうまく行かないのです。
変数変換の理論と関数行列式:2変数の場合
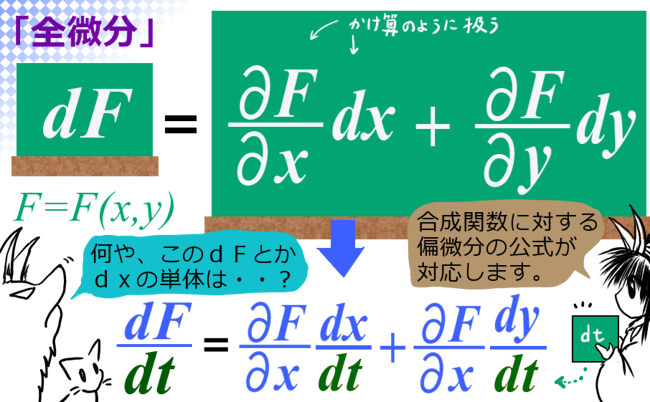
1変数の積分での x=x(t) という変数変換では、積分時に(dx/dt)というオマケが必ずついてきました。では、多変数の重積分の場合は、このオマケの部分はどうなるのでしょうか?
この場合は、x=x(u、v), y=y(u, v)である時の長方形の面積 dudvと、それに対応するxy平面での領域の面積比が、積分計算の時に必ず乗じられるのです。この計算を行うには、偏微分を用います。
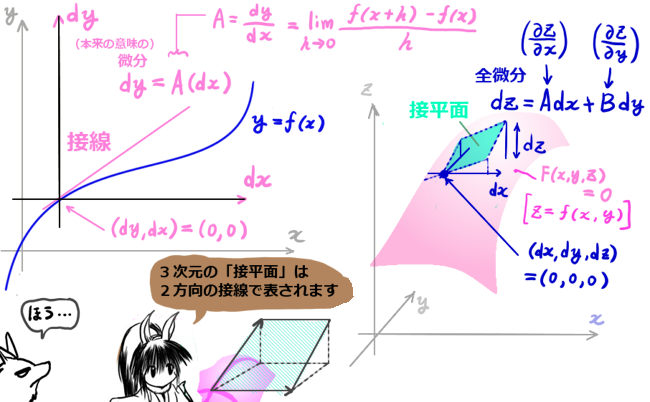
平面の領域にてきとうにたくさんの点を打って結び合わせる事で、領域を小さな三角形の集まりに近似できます。(もちろん数学的には、正確な領域の面積との差を無限に小さくできるという事です。)
今、それらの点がxy平面上のu曲線、v曲線上に打たれていると考えます。 u曲線とv曲線を、非常に細かい「折れ線」であると考えます。
ここでのポイントは、1つ1つの微小な線分を「偏微分係数」であると考える事です。duに対してx方向には (∂x/∂u)du 、y方向には(∂y/∂u)duの変化があるベクトルが伸びるわけです。【具体的な点では偏導関数の変数に値を代入。】これは図で考えたほうが分かりやすいと思います。
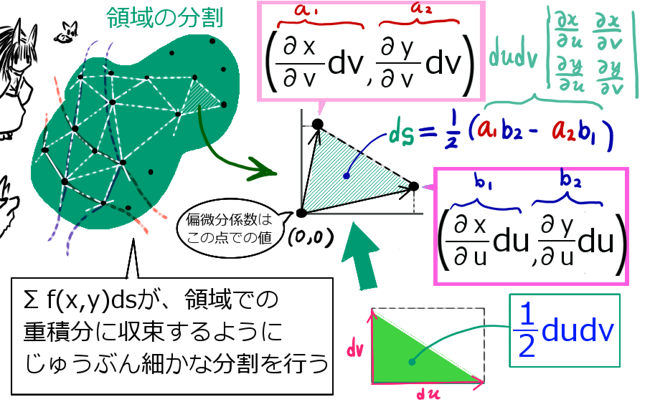
底辺×高さの計算で、高さは「1つのベクトルの長さ×正弦(sinθ)」で表せます。
これについて 成分計算を行うと、ベクトルの成分を用いて簡単に表せるのです。
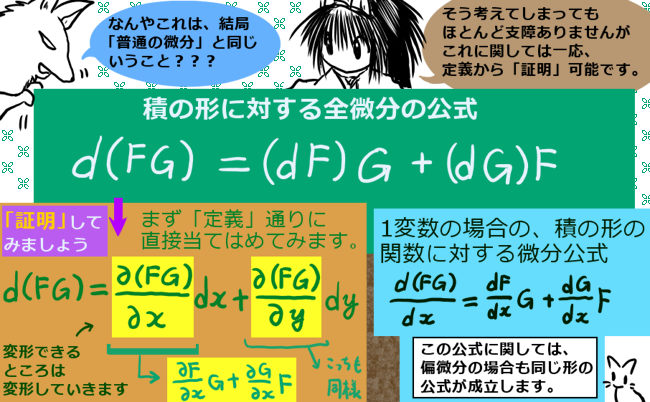
すると、各点から始まる微小三角形の面積は、平面ベクトルの公式(ベクトルによる平行四辺形の面積公式)により、次のように表せる事が分かります:
うしろにくっついてくる偏微分で表される部分が面積比であり、
この形は行列に対する「行列式」の形になっているので「関数行列式」とも言います。
x=x(u、v), y=y(u, v)である時、 $$\frac{\partial x}{\partial u}\frac{\partial y}{\partial v}-\frac{\partial x}{\partial v}\frac{\partial y}{\partial u}\hspace{5pt}を「関数行列式」と呼び、$$ $$\left|\frac{\partial (x,y)}{\partial (u,v)} \right|\hspace{5pt}と表記します。$$
この関数行列式は、某学者のイニシャルをとってJで表記する事もあります。
◆行列式の定義については、2変数は簡単ですが3変数以上は多少込み入った考え方をします。ただし、そのように定義する事によって、いくつかの行列式の公式が成立したりします。
十分小さな微小三角形の面積と、その領域上のある関数の値を掛け合わせて全て加え合わせたものが定積分の値であり、その値は積分を微分の逆演算と考えて計算した値と等しくなるという事は、1変数の積分と全く同じです。まとめると、2変数の場合の重積分の変数変換の公式は次のようになります:
x=x(u、v), y=y(u, v)である時、
$$\int_{y1}^{y2}\int_{x1}^{x2} F(x,y)dxdy=
\int_{v1}^{v2}\int_{u1}^{u2} \left|\frac{\partial (x,y)}{\partial (u,v)} \right|F(x,y)dxdy$$
具体的な定積分を行う時には、関数行列式の計算を忘れない事と、
xy平面の領域と、uv平面の領域を1対1にきちんと対応させる事が重要になります。
尚、証明はやや複雑になりますが、三角形ではなく「平行四辺形」で考える事も可能です。
3変数以上の場合の重積分の変数変換
さて、では3変数の時に x=x(u, v, w), y=y (u, v, w) , z= (u, v, w ) という変換をする場合や、4変数、5変数になった場合はどうなるのでしょうか。
この場合、式自体は変数が増えるごとにどんどん複雑になっていって手計算では手に負えなくなりますが、じつは一応規則性はあるのです。結論を言いますと、「n変数→別のn変数」の変換に対しては、n次の関数行列式を乗じればいいのです。2変数の場合は2次の関数行列式というわけです。
n変数に対して別のn変数に変換する時、つまり
$$X_1=X_1(u_1,u_2,u_3,\cdots,u_n),X_2=X_2(u_1,u_2,u_3,\cdots,u_n),\cdots,X_n=X_n(u_1,u_2,u_3,\cdots,u_n)の時$$
$$\int_{x11}^{x12}\int_{x21}^{x22}\cdots\int_{xn1}^{xn2} F(X_1,X_2,\cdots,X_n)dX_1dX_2dX_3\cdots dX_n$$
$$=
\int_{u11}^{u12}\int_{u21}^{u22}\cdots\int_{un1}^{un2} \left|\frac{\partial (X_1,X_2,\cdots,X_n)}{\partial (u_1,u_2,u_3,\cdots,u_n)} \right|F(X_1,X_2,\cdots,X_n)du_1du_2du_3\cdots du_n$$
が成立します。
一般のn変数の場合だと式が少々込み入りますが、要するに変換の式を代入して関数行列式を掛けてから積分の計算を行えばいい、という意味です。
この場合の関数行列式の作り方は、行列の行の部分にx、y、z、・・を対応させ、列の部分に対して偏微分する変数u、v、w、・・を対応させ、行列式を作るという形になります。
3変数の場合は、次の形の行列式を考える事になります:
$$\left|\frac{\partial (x,y,z)}{\partial (u,v,w)} \right|=\Large{\left| \begin{array}{ccc} \frac{\partial x}{\partial u}&\frac{\partial x}{\partial v}&\frac{\partial x}{\partial w}\\ \frac{\partial y}{\partial u}&\frac{\partial y}{\partial v}&\frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u}&\frac{\partial z}{\partial v}&\frac{\partial z}{\partial w}\end{array}\right| }$$
3変数の場合には空間上の4点を結ぶ事で4面体の集まりとして近似する事が(必ず)できますが、じつは3次元空間での「平行6面体の体積」が行列式の形でうまく表現できるという命題があります。
そこで、dudvdwという「立方体」の体積と、対応するxyz空間上の領域の体積比がうまい具合に関数行列式で表せるというわけです。4変数以上の場合は図にはうまく描けなくなりますが、考え方としては同じで、dudvdwdtといった量と、対応する領域の量の比を考えるわけです。
ただし、これは数学的な理論としてはそうなるという事であり、実際問題として4次以上の重積分の変数変換を「手計算」でひたすらやるという作業は、応用上も純粋数学上もほとんどないと言ってよいかと思います。他方で、関数行列式を展開せずにそのままの形で数学的な議論を進める場合や、数値計算を行う場合にはn変数の重積分の変数変換が使われる事もあります。
物理では重積分はどう使われる?
物理で重積分を累次積分で計算する時は、変数変換してから計算する事が比較的多いかもしれません。ただし、変換の仕方は、基本的には極座標や円柱座標などの分かりやすいものが多いです。
(※理論を複雑にしてしまうと応用上の変数変換のメリットがないので、基本的に、式と計算を簡単にするために変数変換を行います。)
また、具体的な定積分の数値の計算はせずに種々の公式や命題を用いて延々と式変形を進めて、最終的には積分の計算が必要なくなる式を理論的に得てから、計算をするという事もよくあります。
例えば、電磁気学では重積分の形の式が非常に多く用いられますが、直接的に重積分を計算するというよりは、モデルの作り方を工夫 する (例えば領域を球面に選ぶなど)事によって、場面に応じて使える公式を得る目的で用いられます。
コンデンサーやソレノイドに対して成立する式などは平易なものですが、おおもとの形には多変数の微分や積分が含まれており、特別な場合をうまく考える事によって式を簡単にしているのです。