カテゴリー: 複素関数論

複素数の極形式（あるいは「極表示」）の定義と計算方法を説明します。これは三角関数と複素数の密接な関係を表すもので、複素数を平面図形的に扱える根拠ともなっています。

複素数の極形式とは？三角関数と複素数の密接な関係

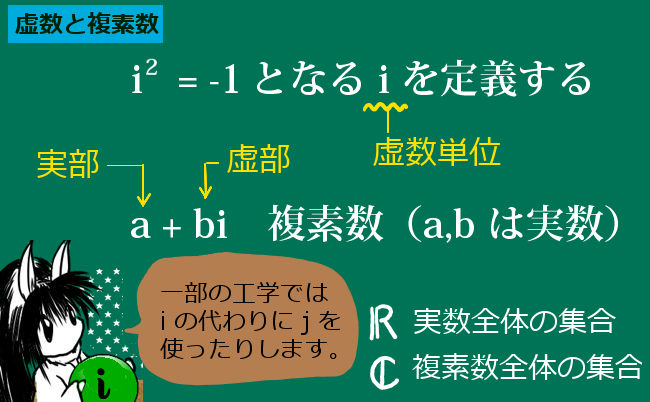
複素数を三角関数で表現したものを複素数の極形式あるいは極表示と呼びます。じつはこれは、複素関数論や物理学等で、複素数を使う場合に本質的に重要になるのです。

複素数を次のように、三角関数を使った形で表したものを複素数の極形式と言います。

式だけ見ると唐突で複雑に見えるかもしれませんが、
じつはこれは図形的に理解してから式の意味を整理すると分かりやすいのです。

複素数の実部を直交座標のｘｙ平面のｘ座標とみなし、
複素数の虚部（の実数係数部分）をｙ座標とみなす考え方があります。
そのように考えた仮想的な平面を複素平面と言い、
その時のｘ軸に相当する軸を「実軸」、ｙ軸に相当する軸を「虚軸」と呼んだりします。
そのように考えると複素数を図形的に捉える事ができるようになり、考察をさらに進めると複素数の極形式の考え方が出てくるのです。

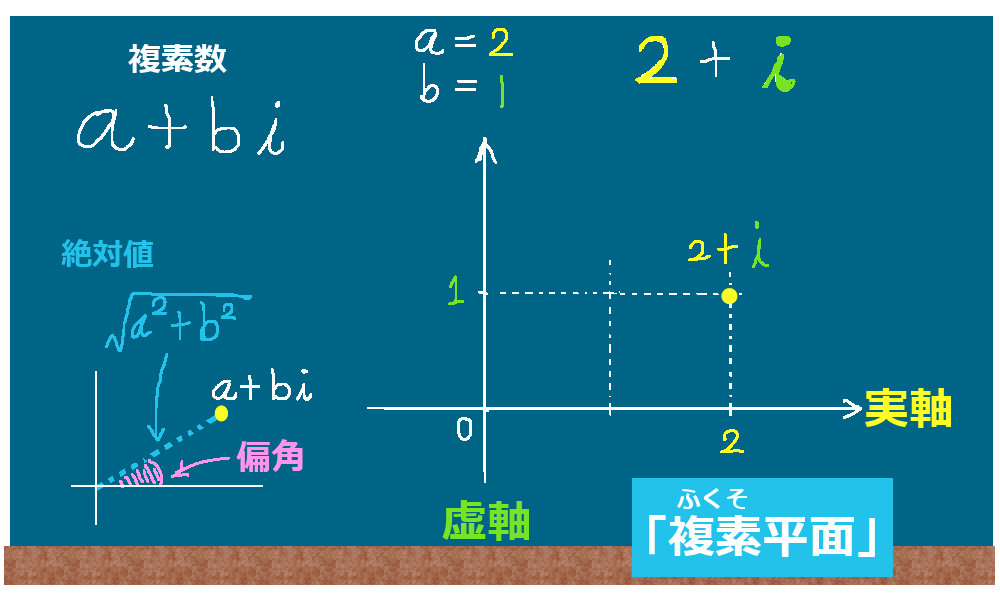
複素平面において、まず「絶対値を原点から複素数までの距離」と考えます。すると、通常のｘｙ平面における極座標の考え方を使えば、複素数の実部と虚部を三角関数を使って表せるはず・・・と考察したものが、上記の複素数の極形式の形なのです。

尚、絶対値を平方根で敢えて書いている部分 \(\cos \theta=\Large{\frac{a}{|z|}=\frac{a}{\sqrt{a^2+b^2}}}\)は、
図で表している部分を式で書いた表現になります。
単純に、直角三角形の１つの辺を斜辺で割った値として余弦や正弦を考えています。
（a や b はマイナスの値もとるので、角度は三角関数に対する一般角を考えている事になります。）

三角関数とみなしている項の部分\(\Large{\frac{a}{|z|}=\frac{a}{\sqrt{a^2+b^2}}}\)と\(\Large{\frac{b}{|z|}=\frac{b}{\sqrt{a^2+b^2}}}\)は、
値が必ず -1 以上 +1 以下です。（２乗してみるとすぐに分かります。）
さらに、これらを２乗して互いを加え合わせたものは１に等しくなります。

$$\left(\frac{a}{|z|}\right)^2+\left(\frac{b}{|z|}\right)^2=\left(\frac{a}{\sqrt{a^2+b^2}}\right)^2+\left(\frac{b}{\sqrt{a^2+b^2}}\right)^2$$

$$=\frac{a^2}{a^2+b^2}+\frac{b^2}{a^2+b^2}=\frac{a^2+b^2}{a^2+b^2}=1$$

これらの事が三角関数の定義と調和しており、
そのために、三角関数としてみなせるという事なのです。

この時に、三角関数として表すからには「対応する角度が必ず存在する」はずですが、
それは実際に考える事ができるのです。しかもその仮想的な角度は、とりあえず数学上の辻褄合わせで考えておくというだけでなく、複素数の計算理論において重要な量なのです。

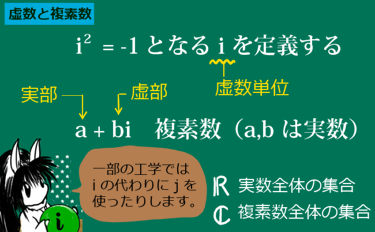
複素数に対して新たに導入した三角関数の角度部分として、新たに設定した実数 θ を、
その複素数の偏角と言います。複素数 z に対して arg z と表記する事もあります。
（英語では偏角の事を argument と言います。）

複素数の乗法と除法、ド・モアブルの定理

複素数を極形式で表した時に成立する重要公式があり、それは
「２つの複素数の積は、『絶対値の積』と『偏角の和』で計算できる」というものです。

この公式において絶対値が１で u ＝ w の時、すなわち絶対値が１の複素数のベキ乗（「ｎ乗」の事）を考えた場合の式は特にド・モアブルの定理と呼ばれる事が多いです。

$$ド・モアブルの定理：(\cos\theta+i\sin)^n=\cos(n\theta)+i\sin(n\theta)$$

他方で除法（割り算）の場合には、絶対値の部分を割り算し、割るほうの複素数の偏角にマイナス符号をつけて掛け算します。つまり、除法の場合は偏角部分を引き算する計算になるのです。

この除法に関するほうの公式は、乗法の場合において片方の偏角 φ の符号を入れ替えて －φ に置き換えたものとみなす事もできます。
マイナスの角度というのは、
「平面上で通常の角度の向き（反時計回り方向）に対して『逆の方向（時計回り方向）』」に向けての角度と考える事ができますから、複素平面上の図形的な捉え方においても乗法の場合の公式で統一的に捉える事が可能です。

除法のほうの公式を考えてみると、ド・モアブルの定理においてべき乗の指数であるｎは自然数だけではなく、マイナスの整数であってもよい事が分かります。
実数の１は「絶対値が１で偏角が０の複素数」と同じものである事に注意します。

$$例えば、(\cos \theta + i\sin \theta)^{-2}=\frac{1}{(\cos \theta + i\sin \theta)^2}=\frac{1}{\cos(2\theta) + i\sin(2\theta)}$$

$$=\cos (0-2\theta)+i\sin (0-2\theta)=\cos (-2\theta)+i\sin (-2\theta)$$

公式の証明

複素数の乗法および除法、ド・モアブルの定理の成立根拠は三角関数の加法定理です。

まず、極形式で表した２つの複素数の積をそのまま計算してみましょう。
すると、実部には余弦に関する加法定理、虚部には正弦に関する加法定理の形が現れるので、加法定理によって変形するとそれがそのまま公式の証明になるのです。

$$uw=|u|(\cos \theta + i\sin \theta)|w|(\cos \phi + i\sin \phi)$$

$$=|u||w|\{ \cos \theta \cos \phi – \sin \theta \sin \phi +i(\sin \phi \cos \theta + \sin \theta \cos \phi )\}$$

$$=|u||w|\{\cos (\theta+\phi)+i\sin (\theta+\phi)\}【証明終り】$$

割り算のほうの公式は、偏角に関しては前述の考え方と同じで片方の符号を入れ替えて、
絶対値部分については |w|＝１／|w| の場合を考えればよいことになります。

あるいは、分母の複素数の共役複素数を分母と分子に掛けて直接証明してもよく、
偏角が θ である複素数の共役複素数の偏角は -θ になりますから、掛け算のほうの公式を使えばよい事になります。

$$乗法の公式で\phiを-\phiに置き換えてもいいし、次のようにしても結果は同じです。$$

$$\frac{u}{w}=\frac{u\overline{w}}{w\overline{w}}=\frac{|u||w|(\cos \theta + i\sin \theta)(\cos \phi – i\sin \phi)}{|w|^2}=\frac{|u|}{|w|}\{\cos (\theta-\phi)+i\sin (\theta-\phi)\}$$

さらなる考察

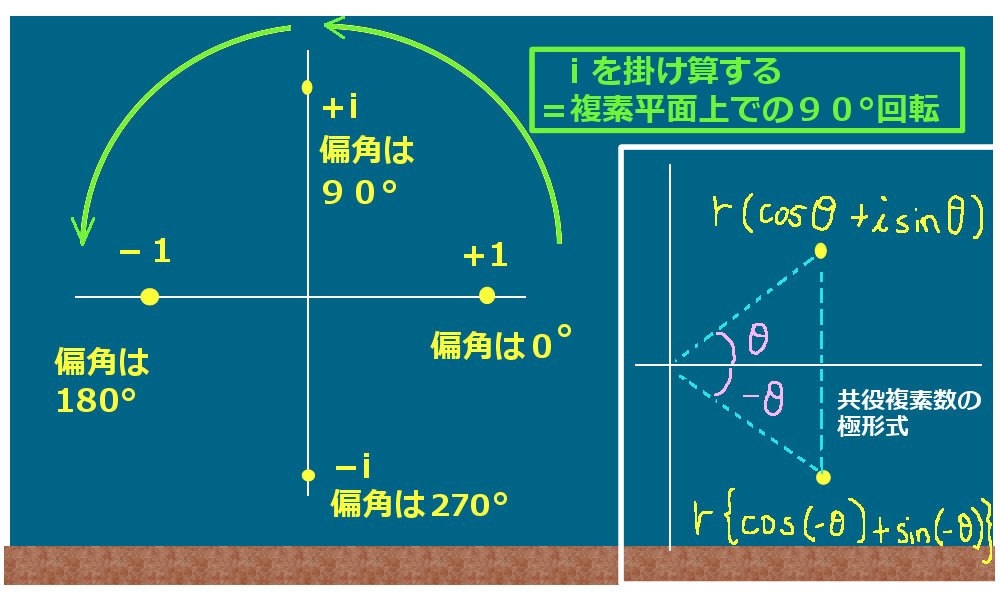
この極形式の観点から言うと、虚数単位 i は

$$i = \cos \frac{\pi}{2}+i\sin \frac{\pi}{2}$$

とも書ける事は重要です。
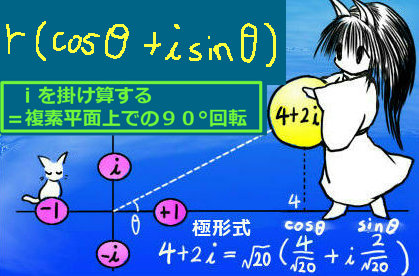
複素数の乗法に関する公式とも合わせて考えると、ある複素数に対して虚数単位 i を掛ける操作は、
「複素平面上では『９０°回転』を意味する」という事が分かります。
物理学や一部の工学では、その分だけ「『位相』を進める」といった表現がされる事もあります。

式で書くと次のようになります。

$$i(\cos\theta+i\sin\theta)=\left(\cos \frac{\pi}{2}+i\sin \frac{\pi}{2}\right)(\cos\theta+i\sin\theta)=\cos\left(\frac{\pi}{2}+\theta\right)+i\sin\left(\frac{\pi}{2}+\theta\right)$$

公式の証明の箇所でも触れましたが、
ある複素数の共役複素数は、偏角の符号を入れ替えたものになります。
その事は図形的に見て確認する事もできますが、
虚部の符号を入れ替える事と、cos(－Θ)＝cos および sin(－Θ)＝－sinΘ の関係から見る事もできます。

$$z=\cos\theta +i\sin\thetaに対して、\overline{z}=\cos\theta -i\sin\theta=\cos(-\theta) +i\sin(-\theta)$$

また、極形式で書いた場合でも「ある複素数と共役複素数の積は、絶対値の２乗になる」という事が確かに成立する事が分かります。ある複素数とその共役複素数は、絶対値は同じである事に注意すると次のような計算になります。

$$z\overline{z}=|z|(\cos\theta+i\sin\theta)\cdot|z|\{\cos(-\theta)+i\sin(-\theta)\}$$

$$=|z|^2\{\cos(\theta-\theta)+i\sin(\theta-\theta)\}=|z|^2(\cos 0+i\sin 0)=|z|^2$$

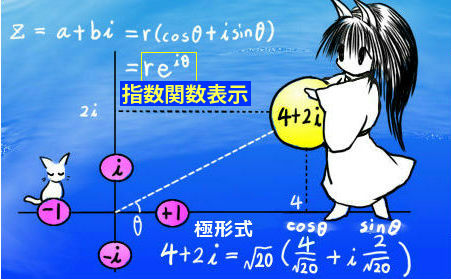
さらに、複素数の極形式を表す別の表記方法として複素数の「指数関数表示」というものがあります。これは「オイラーの式」と呼ばれる事もあります。

$$複素数の指数関数表示：e^{ix}=\cos x +i\sin x$$

e は自然対数の底（ネイピア定数）です。このような複素数が混じった指数関数においても、微積分を含めて通常の指数関数と同様の計算が成立します。複素数の乗法と除法の公式を考えると、指数関数の極形式における乗法や除法の計算と実は調和しています。

例えば指数関数の計算規則に従うと複素数の積は次のようになります。

$$e^{ix}e^{iy}=e^{i(x+y)}$$

これをよく見ると、複素数の極形式における乗法の計算と調和しているのです。

$$(\cos x + i\sin x)(\cos y + i\sin y)=\cos (x+y)+i\sin (x+y) $$