試験というものを度外視して、中学校を卒業した後も(勉強を続けるなら)必要になるという意味で、中学数学において特に重要な公式等を3つ厳選してみたいと思います。
もちろん、それ以外のものは一切知らなくてもよいという意味ではありません。
ここでは、「特に重要なものを敢えて挙げるとしたら?」という事で挙げてみます。
また、「重要か・重要でないか」という事はどうしても主観的な面があります。「重要な公式」を集めたものは、じつは「数学的な意味での集合」ではない(!)という事が実は言えます。何が重要で何が重要でないかは人によって意味が異なる場合があり、正しいか正しくないかという事を絶対的に決められないからです。ここでは、高校や大学に進学して学習を続けた場合に欠かせないという意味での重要さを考えてみたいと思います。

①三平方の定理(ピタゴラスの定理)
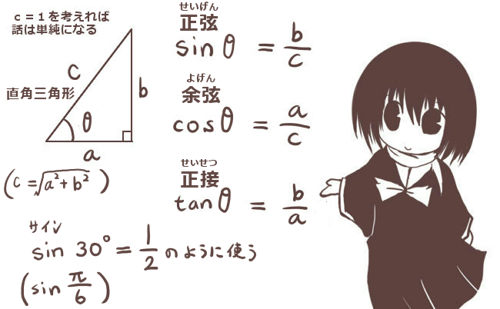
三平方の定理は直角三角形の辺の長さに対して成立する公式で、内容的にはそれほど複雑ではないので比較的分かりやすい公式かと思います。
$$直角三角形の斜辺cと、残り2辺a,bに対してa^2+b^2=c^2$$
基本的には図形に対して成立する公式であるわけですが、三角関数を考えるうえでの基本となる公式であり、直交座標上の2点間の距離を算出するのにも使う公式でもあります。複素数の極形式やベクトルの大きさの定義にも直結している公式であり、数学だけでなく物理学等でも頻繁に使う式になります。
また、間接的に関わる事項として「平方根」の考え方も、三平方の定理を使って2点間の距離を算出するうえで特に必要になるものとなります。数学的にも、「無理数」に属する実数のうち初歩的なものとして2や3などの平方根を挙げる事ができます。

直交座標上の円の式なども三平方の定理を適用しています、
②因数分解と式の展開
2番目に挙げたいのは、もしかすると最も「役に立たないもの」として挙げられる事も多いかもしれない因数分解と、その逆の操作である式の展開です。
$$因数分解(例):x^2 – x=x(x-1)$$
$$式の展開(例):x(x+1)=x^2+x$$
因数分解とは要するに数や式を積(掛け算)の形に直すというだけのものですが、「実数(および複素数)に掛け算して0になる数は『0しかない』」という性質を使って方程式を解く基本的な方法として使われます。また、一見複雑な式を整理するためにも使いますので、数学の理論でも、物理学や工学の理論で数式を扱う際にも、因数分解と式の展開は計算の手法として必須です。
$$方程式の解法(例):x^3-3x^2+2x=0\Leftrightarrow x(x-2)(x-1)=0 \Leftrightarrow x=0,1,2$$
また、物理学等への数学の応用では微積分が重要ですが、微分および積分の初歩的な理論でも因数分解と式の展開は計算を進めるうえで必ず必要になります。

もちろん、因数分解の計算ができる事以上に重要な事として、ここで挙げたいずれの例においても「因数分解の計算」自体は目的ではないのが基本です。数学自体の理論でも、数学を応用する理論でも、基本的に因数分解や式の展開はあくまで計算の手段の1つです。従って、学習の目的を忘れてひたすら「因数分解の計算問題を解く」という事に没頭してしまうと(あるいは没頭させてしまうと)、「役に立たない」という事に繋がってしまうというのは確かに事実でしょう。
③マイナス×マイナス=プラス
3つ目として、因数分解等にも関連しますが、「マイナスとマイナスを掛け算するとプラスになる」という関係式を挙げておきたいと思います。
$$(-1)×(-1)=+1$$
$$計算例:(x-1)(x-2)=x^2-x-2x+2=x^2-3x+2\hspace{10pt}【(-1)×(-2)=+2】$$
この計算は、プラスの値の範囲の計算(例えば個数や金額の計算)ではそれほど重要ではないと言えます。しかし「向き」が関わる計算では重要である場合があり、とりわけ物理学では重要です。
あるベクトルの向きが逆向きである事を表すためにもマイナス符号は使われ、「2回反転させるともとの向きに戻る」といった事も、「マイナスとマイナスを掛け算するとプラスになる」という計算規則と調和するわけです。
また、複素数を構成する虚数単位はi2=-1を満たす「数」として定義されますが、(-1)2=1という計算のもとで、虚数単位iは1とー1以外の数で「4乗すると1になる数」という見方もできるわけです。この事は、より一般的な形で複素数の掛け算についての規則としてまとめられています(「ド・モアブルの定理」)。
そういった理論の考察をする基礎となる事から、(-1)×(-1)=+1という関係式は一見すると奇怪に思う人も多いかと思いますが、特に重要なものとしてここで挙げておきたいと思います。
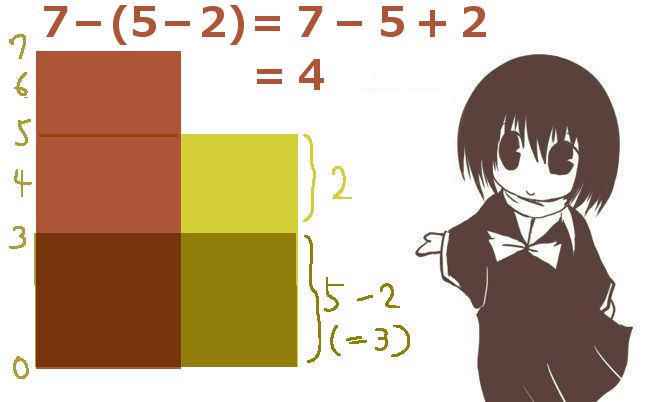
この時、7から5を引いたら2で、元々の7-3=4から見ると多く「引き過ぎ」です。そこで、引き過ぎている分である2を加える、つまりプラスの値として加算すると正しい計算結果になります。
式と計算規則に対して、このような意味付けをする事は可能です。
この他に、マイナスの符号をプラス符号の「逆向き」として捉える例などもあります。