算数や数学ではいろいろな図形について学びます。
算数や数学という「数」を扱う勉強でなぜ「図形」の事を学ぶのかと疑問に思う人もいるかもしれませんが、基本的には算数や数学で扱うのは「図形の長さ」「広さ」「角度」・・といった、数量の計算として扱える部分です。
つまり図形に関して、長いとか短い、広いとか狭い、角ばっている、丸まっているなどといった特徴を数の大小として扱ったり計算したりする事を、算数や数学において学びます。あるいは、高校数学以降で教えられる内容ですが、例えば円と楕円の違いは何かといった事を数量によって特徴づけるという事をしたりします。
平面の図形を構成するもの
「形」あるいは「図形」には、丸(「円」【えん】)、三角形、四角形、六角形、楕円など色々なものがあります。これらは紙の上に描けるような平面図形です。あるいは、放物線や双曲線などのように、平面上で一定の形を持ちながらも延々と果てしなく続くものも図形と呼ぶのが普通です。
平面図形を構成するパーツとして、「点」と「線」があります。
「線」の中には「直線」と「曲線」があります。
いくつかの線や1つの曲線で囲まれる(「閉じている」)部分は「領域」と言ったりします。
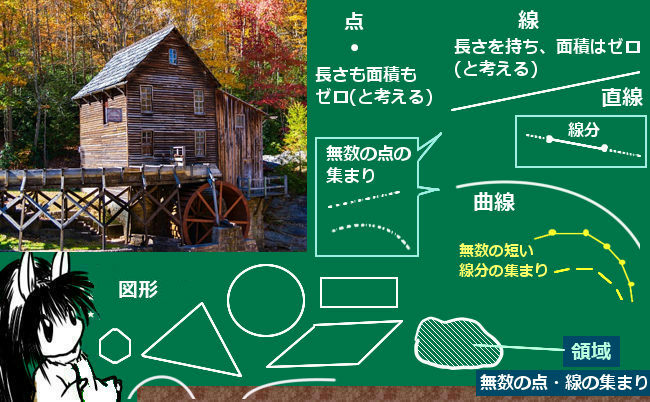
- 点・・1つだけポチっと平面上に打たれる「点」。長さがゼロ。
- 線・・無数の点の集まりで、長さを持ち、面積はゼロのもの
- 直線・・まっすぐな線。【平面上で2点間が最短距離になる】
直線上の2点間だけで構成される部分を特に「線分」(せんぶん)と言います。 - 曲線・・曲がった線。無数の細かい直線の集まりともみなせる。
- 直線・・まっすぐな線。【平面上で2点間が最短距離になる】
- 領域・・平面上で面積を持つ部分。線で区切られる・囲まれる場合が多い。
無数の点・線の集まりともみなせる。
※領域の面積は必ずしも有限ではなく無限大でも可です。例えば平面全体、直線で区切られた平面の半分などを領域として考える事もできます。
これらは平面だけでなく、空間の図形を構成する部品でもあります。
直線で作られる平面図形
平行でない3本以上の直線を用意すると、領域を持つ図形を作れます。これが三角形、四角形、五角形、六角形、n角形・・などと呼ばれるもので、一般に「多角形」とも言います。
【3本以上の直線を用意しても、それらが「同じ1点で交わってしまう」場合には多角形はできません。】
多角形の、角ばっているところに対応する点(2直線が交わっている点)を「頂点」と言い、頂点同士を結ぶ線分を「辺」と言います。
図形ですから、図で見たほうが早いでしょう。
ただし、何かを計算したり証明したりする時には言葉で説明・表現できる事も重要である場合もあります。
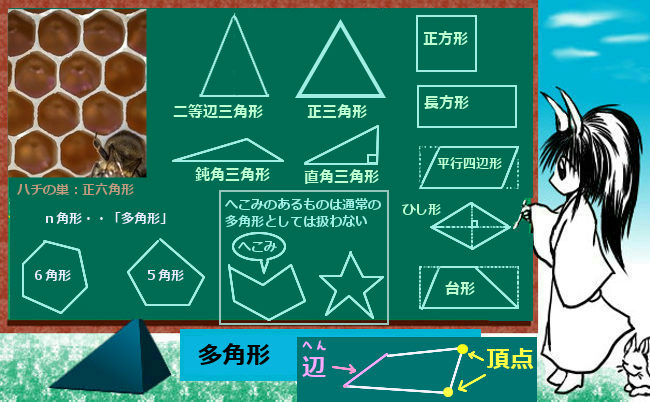
辺の長さが全て等しく、それぞれの内側の角度(内角)の大きさも等しい多角形を、特に「正三角形」「正四角形(=正方形)」「正五角形」「正六角形」「正n角形」・・のように呼び、これらを一般的にまとめた「正多角形」という表現も使います。
■多角形を考える時には、基本的に「へこんでる部分」がないように考えます。これは、辺同士のなす角のうち図形の内側にあるもの(「内角」)の大きさが180°未満であるとも表現できます。
ですから例えば星形の「☆」の図形などは、辺同士の交点が10個ありますが、これは10角形とは呼ばない事にするという決まりにしています。へこんでいる部分を含むためです。
へこんでいる事を凹(おう)、角ばっている事を凸(とつ)の漢字で表す事もあります。この凹・凸というのは数学独自の記号ではなく、一般にも一応使われる漢字です。
■三角形については辺の長さが等しいという時点で角度も全て等しくなります。しかし、四角形の場合だと辺の長さは等しく、角度は全て同じわけではないという場合(ひし形)があり得ます。同様に他の多角形でも、各辺の長さは全て等しいけれど内角の大きさが異なる場合はあり得ます。
三角形と四角形に関しては、特別な性質を持つものに別途名前をつけています。
- 正三角形・・3辺の長さが全て等しい三角形
- 二等辺三角形・・2辺の長さが等しい三角形
【その意味で正三角形も二等辺三角形に含まれます。】 - 直角三角形・・1つの角度の大きさが直角(90°)である三角形
- 鋭角三角形・・3つの角度の大きさ全てが、それぞれ90°未満である三角形
【鋭角は「えいかく」と読みます。】 - 鈍角三角形・・1つの角度の大きさが90°を超える三角形
【鈍角は「どんかく」と読みます。】 - 直角二等辺三角形・・二等辺三角形のうち、1つの角度の大きさが直角である三角形
- 正方形・・「正四角形」の通称。4つの辺の長さが全て等しく、内角の大きさが直角。
- 長方形・・向かい合う辺(対辺)の長さが等しく、内角の大きさが直角である四角形
正方形も長方形に含まれます。 - 平行四辺形・・向かい合う辺が互いに平行である(この時、長さも等しくなる)四角形。
正方形、長方形も平行四辺形に含まれます。 - ひしがた【菱形】・・平行四辺形のうち、辺の長さが全て等しいもの。
(※内角は等しくなくても可。ただし、対角は必ず等しくなる。)
正方形は、ひし形に含まれます。
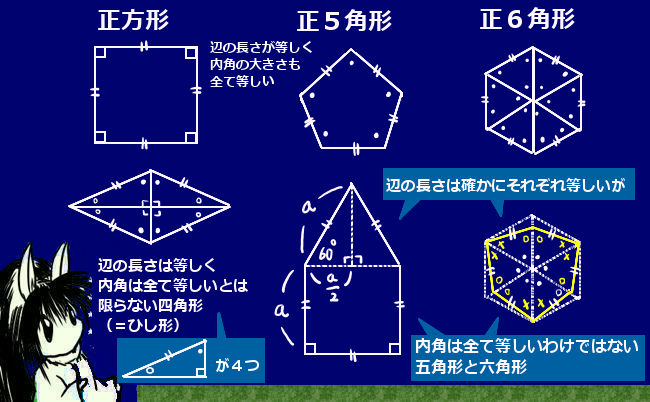
ひし形については、4つの合同な直角三角形で構成できる事から、平行四辺形でもある事や、対角線が直交する事などが分かります。
五角形については正方形に正三角形をつなぎ合わせたもの、六角形については三角形を軸対称に反転させながら作ったものなどが例として挙げられます。
三角形については多くの平面幾何の性質があります。
曲線による平面図形
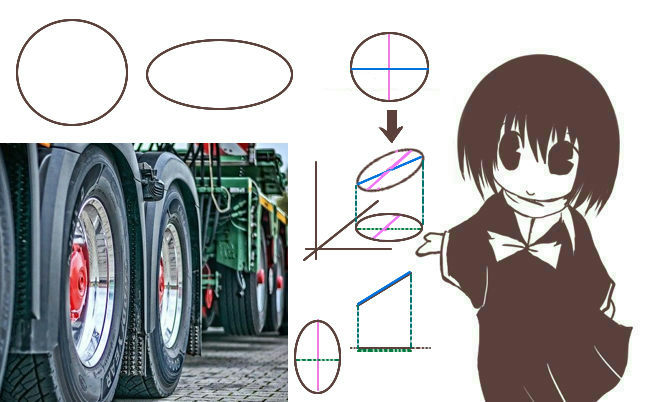
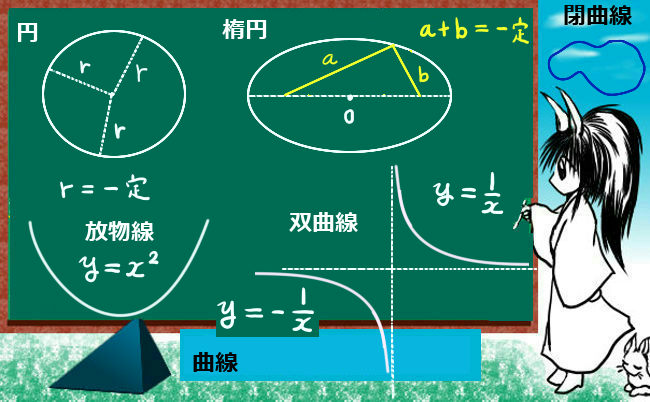
曲線で作られる図形については、一番簡単なものが「円」です。円は「中心からの距離が等しくなる」図形(点の集まり)で、何かを固定してその周りを回転させると得られるものなので身の回りにもボール・何か巻いてある芯の断面、車輪や水車などで広く見られる形です。

他方、円を1つ以上の方向にだけ引き延ばす、あるいは縮小した「楕円」もあります。(定義は「2定点からの距離の和が等しい点の集まり」です。これは中学校では数学としては扱いません。)
身の回りで楕円が見られる簡単な例としては、円状の物を真正面からではなく斜めから見た時に見られる見かけ上の形です。当然ながら円を斜めから見れば1つの方向につぶれて細長く見えるわけですが、もとが円であればそれが楕円の形になります。
これは、正方形を斜めから見ると長方形にも見える、長方形を特定の斜めから見ると平行四辺形に見えるというのと同じ理屈です。
円や楕円のように平面上で曲線が丸まって「閉じた」領域を持つ図形は一般的には「閉曲線」と呼ばれます。
これに対して、放物線や双曲線のように閉曲線ではない曲線もあります(「開曲線」とも言います)。
◆参考:接線線積分の定義と考え方(微積分を含みますが、曲線を対象とする積分理論の1つの例です。)

関数で言うと、2次関数y=x2は放物線、
反比例の関数y=1/x(とy=-1/x)は双曲線に該当します。
円に関しては平面幾何上の種々の性質や、円周・面積に関する種々の性質が成立します。