三角比とは直角三角形の2つの辺の比の事で、どの2つの辺を考えるかによって
正弦(「せいげん」)、余弦(「よげん」)正接(「せいせつ」)の基本的な3種類があり、記号ではそれぞれ sin(サイン), cos(コーサイン), tan(タンジェント)で表します。また、その逆数として「余割」「正割」「余接」をもし必要があれば使う事もあります。三角比は図形問題を考える時にも使えますがベクトルを考えるうえでも重要で、ベクトルを力学等で活用する時にも使用されます。
三角形の角の角度は基本的には0度より大きく180度未満ですが、それを拡張して三角比に対して変数を任意の実数としたものは特に三角関数と呼ばれます。三角関数は周期関数として代表的なものであり、数学的にも物理的にも応用の範囲が広い初等関数の1つです。
角度を表す記号は何でも良いのですが
特に多く使われるのがθ(「シータ」あるいは「テータ」英語で言うthの音を表すとされるギリシャ文字)であり、ここでも一般的な角度を表す記号として多く使用します。
三角関数はxy平面の座標上で原点を中心とした単位円周上の座標としても考える事ができる事などから円関数と呼ばれる事もあります。ただしこのサイトでは三角関数の名称を使用します。
■サイト内関連記事:
- 一般角の定義と使い方
- 波動の用語と定義【正弦波】(物理での三角関数の使われ方の例)
- 光の二重スリット干渉実験【ヤングの実験】
- ベクトルの内積の定義(ベクトルでの余弦の使われ方)
- ベクトルによる平行四辺形の面積公式(正弦を考えます)
- 方向余弦の定義と公式
- 複素数の指数関数表示(複素数での使われ方)
- 加法定理(証明と使い方)
- 余弦定理
- 正弦定理
- 弧度法とラジアン(180度をπとして表す角度の表記法)
- 初等関数の微分公式(三角関数の微分公式等)
- 逆三角関数(三角関数の逆関数)
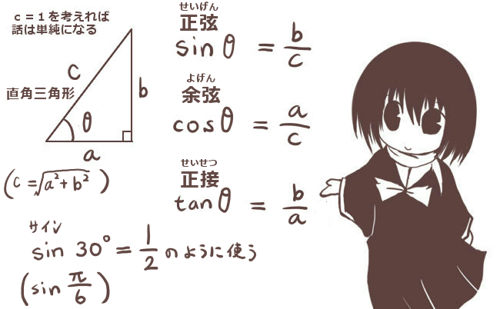
三角比(正弦・余弦・正接)の図形的な定義
三角比は直角三角形の辺の比であり、角度を変数として表されます。
三角形の各辺の比は相似である別の三角形でも同じ値ですから、三角比は直角三角形の大きさにはよらず角度によってのみ確定する値になります。角度によって1つの値が決まる事を意味します。
斜辺と底辺と高さの部分(直角以外の2つの角度のどちらを考えるかで底辺と高さは入れ替わります)を使用し、「sin(サイン)」「cos(コーサイン、コサイン)」「tan(タンジェント)」の記号を使って角度の関数として表します。
直角三角形の斜辺以外の1つの辺を底辺とした時に、斜辺と底辺のなす角度をθとします。斜辺の長さをc,斜辺と共に角をなす辺の長さをa(図では底辺),もう1つの辺の長さ(図では高さ)をbとする時、三角比の基本となる正弦・余弦・正接は角度θの関数としてそれぞれ次のように表されます。
| 三角比 | 表記 | 辺の比で表した時 | 具体例 |
| 正弦 | sinθ | b/c | sin60°=\(\frac{\Large \sqrt{3}}{\Large 2}\) |
| 余弦 | cosθ | a/c | cos60°=\(\frac{\Large1}{\Large 2}\) |
| 余弦 | tanθ | b/a | tan45°=1 |
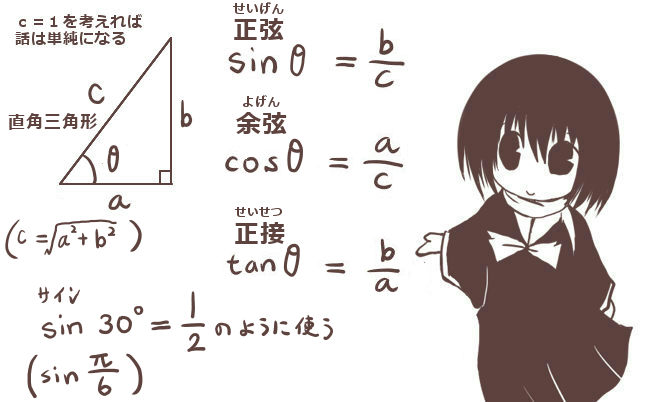
考えているのが直角三角形なので三平方の定理によりa2+b2=c2ですが、これは必要がある場合には三角比を表すのにも使用します。例えば斜辺の長さcを使わずにaとbだけで正弦と余弦を表すなら次のように書けます。
$$\sin\theta=\frac{b}{\sqrt{a^2+b^2}}\hspace{15pt}\cos\theta=\frac{a}{\sqrt{a^2+b^2}}$$
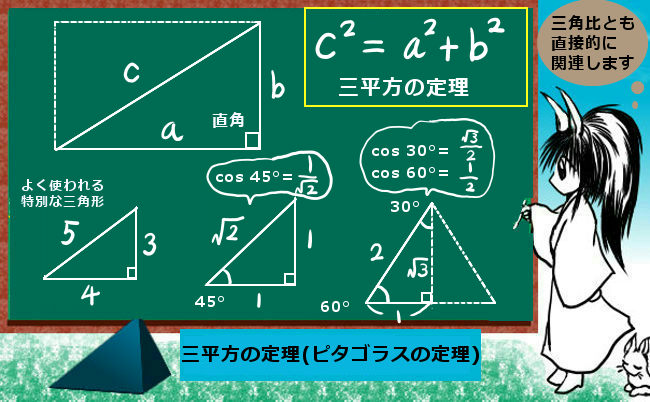
30°、45°、60°の三角比の具体的な値は図形的な考察から導出する事ができて、整理すると次のようになります。
| 三角比の値 | 30° | 45° | 60° |
| 正弦 sinθ | \(\frac{\Large1}{\Large 2}\) | \(\frac{\Large 1}{\Large \sqrt{2}}\) | \(\frac{\Large \sqrt{3}}{\Large 2}\) |
| 余弦 cosθ | \(\frac{\Large \sqrt{3}}{\Large 2}\) | \(\frac{\Large 1}{\Large \sqrt{2}}\) | \(\frac{\Large1}{\Large 2}\) |
| 正接 tanθ | \(\frac{\Large 1}{\Large \sqrt{3}}\) | 1 | \(\sqrt{3}\) |
sin45°=cos45°となっている事などは偶然の一致ではなく図形的な関係から成立します。
図形的にこれらの値を導出するには次のようにします。
60°の場合は1辺の長さが「2」の正三角形を考えると分かりやすく、
真っ二つにすると斜辺が2、底辺が1、高さが\(\sqrt{3}\)の直角三角形ができます。
するとまず、余弦についてcos60°=1/2が分かります。
次に高さ部分については三平方の定理を使って \(\sqrt{2^2-1^2}=\sqrt{4-1}=\sqrt{3}\) と計算します。
それによってsin60°=\(\sqrt{3}\)/2およびtan60°=\(\sqrt{3}\)を導出できます。
30°の場合は、直角三角形の残りの角度が90°-60°=30°である事を使います。すると底辺と高さの関係が変わるので、正弦と余弦に関しては60°の時の値を入れ換えた形になり、正接に関しては60°の時とは逆数の関係になるわけです。三角形の向きを変えて考えてみても同じ事になります。
45°の場合には直角二等辺三角形を考えて、底辺と高さをそれぞれ1とすれば、まず正接について tan45°=1が分かります。次に斜辺の長さは\(\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}\) となるので正弦と余弦の値も導出できます。
角度を0°より大きく90°未満とした時の三角比の取り得る範囲は次のようになります。
- 0<sinθ<1【θに対して単調増加】
- 0<cosθ<1【θに対して単調減少】
- 0<tanθ 【θに対して単調増加で、90°に近付くにつれて無限に増加】
その他の角度についての三角比の値を知るには加法定理によって一部の値を計算できるほか、正弦についての無限級数展開(マクローリン展開)を使います。$$\sin \theta=\theta – \frac{\theta^3}{3!}+\frac{\theta^5}{5!}-\frac{\theta^7}{7!}+\cdots$$ただし、この式を使う時には角度は弧度法で表したものでなければなりません。
例として、10° は弧度法で\(\pi\)/18【rad】なので、式に代入して四捨五入で小数点第3位まで計算すると sin10° ≒ 0.1735 です。
角度が弧度法で0に近い値の時はsinθ≒tanθ≒θの近似式を使えます。(上記の展開式で第2項以降をほぼ0と考える事により得られます。)
10°に相当する弧度法の角度を小数で表すと\(\pi\)/18≒0.1744なので、10°の場合は概算的にはその近似式を使ってもよいと言えます。
三角関数の定義と考え方
三角比に対して適用する角度の範囲を0°以下や90°以上の値を考えた関数を三角関数と呼びます。三角関数の角度は基本的に弧度法を使って表記しますが、ここでは分かりやすさのために変数を度数法で記しておきます。また、三角関数を使う時には変数をxとする事も多いですが、ここでは変数をθで表すとします。
任意の実数値を取り得る角度(「一般角」)は図形的には直角三角形を反転させた時に意味を持ち得ると同時に、向きも含めた回転の意味も持ちます。直交座標上で原点を中心にして見た時に反時計回りの回転がプラスの方向への角度の増加、時計回りの回転がマイナス方向への角度の減少としての意味を持ちます。
360°に達した時は「1周」とみなします。三角関数は360°を経過するごとに0°の時と同じ値になると定義します。つまり周期的に同じ値を繰り返す周期関数となるわけです。
三角関数の値は、xy直交座標上の原点を中心とした半径1の円(単位円)の円周上の点の座標として表されます。より具体的にはx軸のプラスの部分を0°として、角度θになる直線を円に向かって引いた時の円との交点のx座標を余弦関数 cosθの値として、y座標を正弦関数 sinθの値とします。この時に、角度の範囲が0°より大きくて90°未満の時には三角比と全く同じ値をとるわけです。
sin0°=0,cos0°=1,sin90°=1,cos90°=1のように定義します。このような定義をするのは数学的な拡張として自然であるからというのもありますが、物理的に単位円周上の等速運動に対応する単振動などを考えてみるとそれを表現する関数として適切であるといった見方もできます。
正接関数はtanθ=(sinθ)/(cosθ)として定義します。ただし、正接関数においては cosθ=0となるθの値においては無限大になってしまい「定義できない」とします。より具体的にはθ=±90°,±270°等は正接関数の定義域から除外する事になります。
三角関数の具体的な値を、三角比の範囲も含めて挙げてみると次のようになります。
| 一般角(度数表記) | 正弦関数 sinθ | 余弦関数 cosθ | 正接関数 tanθ |
| 0° | 0 | 1 | 0 |
| 30° | \(\frac{\Large 1}{\Large 2}\) | \(\frac{\Large \sqrt{3}}{\Large 2}\) | \(\frac{\Large 1}{\Large \sqrt{3}}\) |
| 45° | \(\frac{\Large 1}{\Large \sqrt{2}}\) | \(\frac{\Large 1}{\Large \sqrt{2}}\) | 1 |
| 60° | \(\frac{\Large \sqrt{3}}{\Large 2}\) | \(\frac{\Large 1}{\Large 2}\) | \(\sqrt{3}\) |
| 90° | 1 | 0 | 定義しない |
| 120° | \(\frac{\Large \sqrt{3}}{\Large 2}\) | \(-\frac{\Large 1}{\Large 2}\) | \(-\sqrt{3}\) |
| 135° | \(\frac{\Large 1}{\Large \sqrt{2}}\) | \(-\frac{\Large 1}{\Large \sqrt{2}}\) | -1 |
| 150° | \(\frac{\Large 1}{\Large 2}\) | \(-\frac{\Large \sqrt{3}}{\Large 2}\) | \(-\frac{\Large 1}{\Large \sqrt{3}}\) |
| 180° | 0 | -1 | 0 |
| 210°【-150°と同じ】 | \(-\frac{\Large 1}{\Large 2}\) | \(-\frac{\Large \sqrt{3}}{\Large 2}\) | \(\frac{\Large 1}{\Large \sqrt{3}}\) |
| 225°【-135°と同じ】 | \(-\frac{\Large 1}{\Large \sqrt{2}}\) | \(-\frac{\Large 1}{\Large \sqrt{2}}\) | 1 |
| 240°【-120°と同じ】 | \(-\frac{\Large \sqrt{3}}{\Large 2}\) | \(-\frac{\Large 1}{\Large 2}\) | \(-\sqrt{3}\) |
| 270°【-90°と同じ】 | -1 | 0 | 定義しない |
| 300°【-60°と同じ】 | \(-\frac{\Large \sqrt{3}}{\Large 2}\) | \(\frac{\Large 1}{\Large 2}\) | \(-\sqrt{3}\) |
| 315°【-45°と同じ】 | \(-\frac{\Large 1}{\Large \sqrt{2}}\) | \(\frac{\Large 1}{\Large \sqrt{2}}\) | -1 |
| 330°【-30°と同じ】 | \(-\frac{\Large 1}{\Large 2}\) | \(\frac{\Large \sqrt{3}}{\Large 2}\) | \(-\frac{\Large 1}{\Large \sqrt{3}}\) |
| 360°【0°と同じ】 | 0 | 1 | 0 |
座標上の単位円から判断するか三角比の値をもとに公式から計算するものになります。
基本的には三角比の値を使う事ができて、それがx軸対称やy軸対称の形で符号が入れ替わったり角度を180°から引いた形で扱うといった計算をしている事になります。
三角比と三角関数の公式
基本公式としては次のようなものがあります。三角比と三角関数とで同じ公式を適用する事ができて、違いは定義域(角度の範囲)だけになります。三角関数で統一的に考えて、三角比は範囲を限定した特別な場合と考えても同じです。
正弦、余弦、正接について次式が成立します: $$\tan\theta=\frac{\sin\theta}{\cos\theta}$$ $$(\cos\theta)^2+(\sin\theta)^2=1$$ $$【\cos^2\theta+\sin^2\theta=1と一般的に書きます。】$$ $$\cos (90°-\theta)=\sin \theta$$ $$\sin (90°-\theta)=\cos \theta$$ $$\tan (90°-\theta)=\frac{1}{\tan\theta}$$
三角比の2乗については、次のように書く習慣があります。
$$\sin^2\theta\hspace{15pt}\cos^2\theta\hspace{15pt}\tan^2\theta$$
また2乗だけでなく、3乗、4乗等でも同じようにします。
これは一応「ある角度の2乗」θ2の三角比 sin(θ2)と区別するためです。
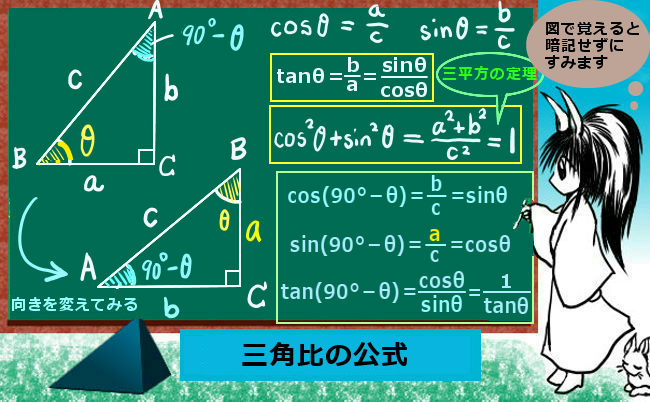
上記の公式の第1式である正接を正弦と余弦で表す関係は、単純に正弦を余弦で割ると出ます。斜辺の部分は消えてしまうわけです。
$$\frac{\sin\theta}{\cos\theta}=\frac{b}{c}\cdot\frac{c}{a}=\frac{b}{a}=\tan\theta$$
2番目の、正弦と余弦のそれぞれの2乗の和が1になるという式は、三平方の定理により分かります。
$$(\cos\theta)^2+(\sin\theta)^2=\frac{a^2+b^2}{c^2}=\frac{c^2}{c^2}=1$$
90°-θ の角度を考えている関係式は、図を見ると分かりやすいかと思います。直角三角形の θ とは別の角度の三角比は、正弦と余弦の関係をちょうどひっくり返して表せるという事を意味します。
正接の公式tan(90°-θ)については最初の関係式 tanθ=(sinθ)/(cosθ) も使って
{sin(90°-θ)} / {cos(90°-θ)} によって出しています。
正接の公式についてはいずれも同じように導出する事ができます。
特に三角関数に対しては次の式が成立する、あるいは定義が行われます。
| 定義・公式 | 正弦関数 sinθ | 余弦関数 cosθ | 正接関数 tanθ |
| 0° | 0 | 1 | 0 |
| 90° | 1 | 0 | 定義せず |
| マイナス の角度 | sin(-θ) =-sinθ | cos(-θ) =-cosθ | tan(-θ) =-tanθ |
| 180°-θ | sin(180°-θ) =sinθ | cos(180°-θ) =-cosθ | tan(180°-θ) =-tanθ |
| 180°+θ | sin(180°+θ) =-sinθ | cos(180°+θ) =-cosθ | tan(180°+θ) =tanθ |
| 360°+θ | sin(360°+θ) =-sinθ | cos(360°+θ) =-cosθ | tan(360°+θ) =tanθ |
| 90°+θ | sin(90°+θ) =cosθ | cos(90°+θ) =-sinθ | tan(90°+θ) =-(1/tanθ) |
その他、重要となる(他の色々な場面で使う)主な公式や定理には次のようなものがあります。
| 定理・公式等 | 主な内容 | 備考 |
| 余弦定理 | c2=a2+b2-2abcosθ | θはaとbの長さの辺のなす角 θ=90°の時は三平方の定理 |
| 加法定理 | sin(θ1+θ2)=sinθ1cosθ2+sinθ1cosθ2 cos(θ1+θ2)=sinθ1sinθ2-cosθ1cosθ2 | 正接の加法定理も存在 |
| 倍角の公式 | sin(2θ)=2sinθcosθ cos(2θ)=sin2θ-cos2θ | 加法定理から導出 |
| 和積の公式 | sinθ1+sinθ2=\(2\sin\frac{\Large \theta_1+\theta_2}{\Large 2}\cos\frac{\Large \theta_1-\theta_2}{\Large 2}\) cosθ1+cosθ2=\(2\cos\frac{\Large \theta_1+\theta_2}{\Large 2}\cos\frac{\Large \theta_1-\theta_2}{\Large 2}\) | 加法定理から導出 積和の公式もあり |
| 三角間数の 微分公式 | (d/dθ)sinθ=cosθ (d/dθ)cosθ=-sinθ | 微分の定義式より 積分にも使用可 |
| 極座標変換 | x=rcosθ y=rsinθ | 図から導出 |
| 複素数の 指数関数表示 | eiθ=cosθ+isinθ | i は虚数単位 オイラーの式とも |
| マクローリン 展開 | sinθ=θ-θ3/(3!)+θ5/(5!)-・・・ cosθ=1-θ2/(2!)+θ4/(4!)-・・・ | 正接に関しては 逆正接関数のほうが簡単 |
| 内積の定義 | \(\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}|\hspace{2pt}|\overrightarrow{b}|\cos\theta\) | θは2つのベクトルのなす角 |