順列とは、N個のものを並び替える方法を言います。
(英:permutation 順列を「置換」とも言います。)ここでは、その方法が何通りあるかという「場合の数」について説明します。高校数学で扱うのはその事項です。
結論を先に言うと、N個のものを並び替える順列の総数は次式で表されます。
$$_NP_N=N!$$
$$=N(N-1)(N-2)\cdots 3\cdot 2\cdot 1$$
NPNという表記は、N個のうちN個全てを並び替えるという意味です。
びっくりマークは「階乗」を表します。自然数を1ずつ下げてNから1まで掛けて積の形にする事を指します。例えば5!=5・4・3・2・1=120です。
また、N個のもののうち、M個を並び替え方の総数は次の通りです。
このようになるわけですが、これらを「暗記」するのはやめましょう。確かに公式の中には暗記してしまったほうが早いものもありますが、この順列の総数に関する式は「理解」できるものです。

N個のものを並び替える方法
初めに、少ない数から具体的に見てみましょう。
2個のものがあったとき、これを並び替える方法は「2通り」です。{A,B} {B,A} の2通りです。他の文字・・例えば {甲,乙}{乙,甲}の2通りと考えても、何でも構いません。
要するに、順番を区別して数えるという事なのです。
これが「2つのものを並び替える順列の総数」2P2=2の意味です。この場合はとても簡単ですね。
では、A,B、Cあるいは甲、乙、丙などの3つを並び替えるにはどうすればよいでしょう?
これを具体的に書くと、
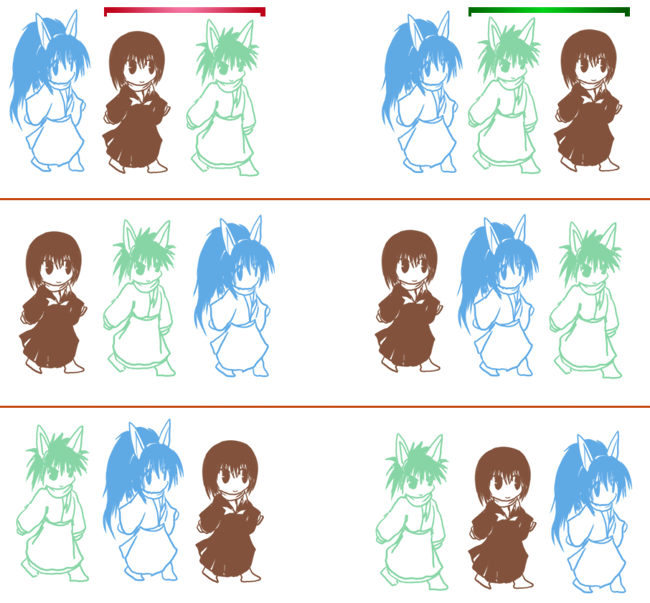
{丙、乙、甲}{丙、甲、乙}{乙、丙、甲}{乙、甲、丙}{甲、丙、乙}{甲、乙、丙}
の6通りあります。
実際これしか順番に並べる方法はないのですが、どのようにしてこれらを書きだしたかを説明します。まず、最初に来る文字が甲、乙、丙の3人のパターンがあります。そしてそれぞれの場合について、続く2人の順番が2通りあります。丙を一番左に置いたとき、続く順番は{乙,甲}と{甲,乙}の2パターンであるという事です。そして次に乙が最初に来る場合を考えて、同様に書きだして上記の6パターンの並びを得ています。
つまり3人それぞれを特定の場所、例えば一番左に置く場合につき2通りあるので3×2=6通りの並び替えの方法があるというわけです。これが3P3=3!=6の意味です。
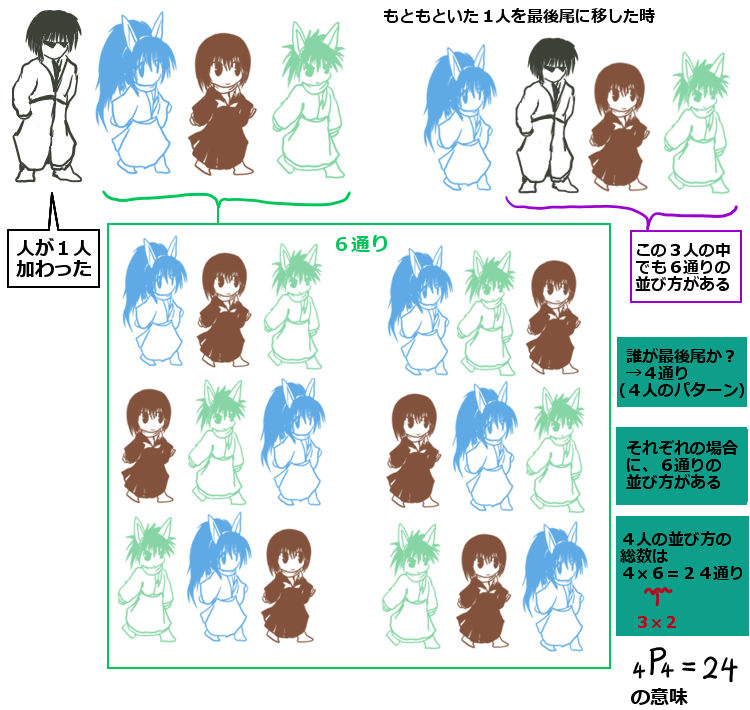
では4人を並び替える場合はどうするかというと、1つの位置(例えば一番左)に誰かをおくと、そのパターンにつき「3人を並び替える方法がある」事に気付くと分かりやすいかと思います。
誰かが一番左にいるごとに残りの3人を並べる方法が6通りあります。一番左に誰が来るかについては全部で4人いるわけですから4通りになります。よって4人を並び替える方法は全部で4×6=24通りです。
ここで、3人を並び替える方法が3×2=6通りであった事を考えると、4人を並び替える方法は4×3×2=24通りであるとも言えます。これが4P4=4!=24の意味です。
では5人になった場合はどうかというと、考え方は同じです。
まず5人のそれぞれをどこか固定した位置に置きます。例えば上の例と同じく一番左に置きます。すると、残りの4人の並び替えは24通り(4!=4×3×2通り)である事が分かっているので、5人のそれぞれに対して24通りですから5×24=120通りの並び替えの方法があります。これをまとめて5!通りと書く事もできて、これが5P5=5!=120の意味です。わずか5人で、並び替えの方法は意外に多いという事が分かります。
6人の場合も同じで、6×5!=6×120=720通りになります。これもこれまでと同様に6!=720通りとも書けます。非常に数が増えて、1つ1つ手で紙に具体的に書きだすのは困難である事が分かります。
7人の場合は7!=7×6!=7×720=5040通りになります。以降、人数を増やしていくと並べ方の総数は莫大に増えていく一方です。
以下、何人いても考え方は同じで、N人いた場合にはまずN人を選びます。のこりN-1人についてみるとこれは(N-1)×「N-2人の場合」ですから、結局N×(N-1)×(N-2)×・・・×3×2=N!通りという事になるわけです。
【NPN=N×N-1PN-1=N×(N-1)!=N!のようにも書けます。考え方はある程度自由です。】
これが「N個のものを並び替える順列の総数は NPN=N!である」という事の意味です。
N個のうちM個を並び替える場合
次に、N個のものの中からM個選んで並び替える方法の総数についてです。
これは順列の記号ではNPMと書きます。
公式だけ見ると一見わけがわからない式に見えるかもしれませんが、意味はじつに簡単です。
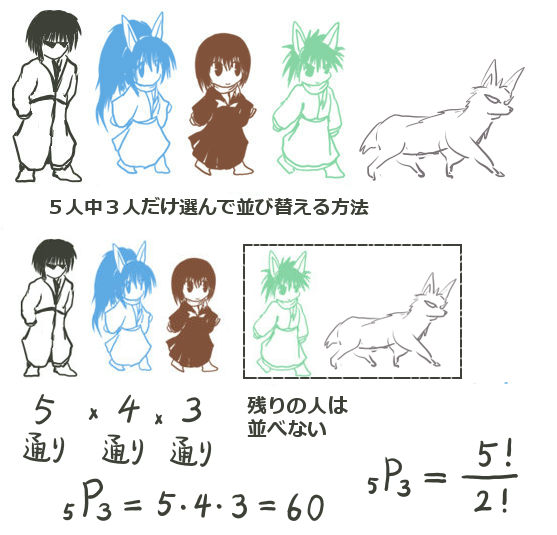
5人いて、3人を選んで並び替える方法を考えてみましょう。
5人全員を並び替える場合には5!=5×4×3×2通りであったわけですが、意味を考えると3人だけを選ぶ場合には、最後の「2倍」がいらないわけです。誰か3人が並んだ時点で、選ばなかった2人も確定しますからそれで終了というわけです。
結果的には話は単純で、最初に5人のうちの1人を選び、次に残った4人の中から1人、続いて残った3人の中から1人を選びそこで打ち切るという事です。
【この方法でN個全てを並び替える場合を理解しても支障ありません。】
式で書くと5P3=5×4×3=60という事です。
5人中2人だけを選び並び替えるなら5P2=5×4=20通り、5人中1人だけなら5P1=5通りです。
この通り、考え方は単純なのですが一般のNに対して式を書くと多少煩雑になる面があります。
N個のうち3個を並び替えるという場合にはN(N-1)(N-2)通りなどと上から順に3項の積を考えて済みますが、N個のうちM個を並び替える場合にはどう書くのかという話になります。
NP3=N(N-1)(N-2)の場合を見てみると、N-3以降の項がないわけですから、N!を(N-3)!で割るとちょうどうまい具合に同じ数になります。
つまり、(N-M)!を考えて、それでN!を割ればうまく式でも表現できるわけです。これがNPMを表す公式の意味です。
$$_N\mathrm{P}_M=\frac{N!}{(N-M)!}$$
尚、M=N-1を考えると、N-M=N-(N-1)=1ですから、それでN!を割ってもN!のままです。NPN-1=NPNという事になります。これは5人全員を並び替える時、最後の一人については空いている位置に入れるだけなので結局「5人中4人を選んで並び替える」場合と同じである事に対応しています。
順列の考え方は、具体的な人や物の並べ方を考える時だけでなく、種々の理論の中でN個の項を並び替える何らかの操作をする時にその総数を表すために使用されます。
例えば(高校数学の範囲外ですが)線型代数で行列式の定義をする時にはN個の項の積をとって並び替えたものを全て考えるという事をやるので、項数は順列の総数という事になります。(N!という形が出てくる式全てが順列に関係するとは限りません。例えば、単項式に対する微分操作を繰り返す事でN!が出てくるパターンもあります。)
また、順列の他に重要な「組み合わせ」の数え方も順列での考え方を基礎としています。方法の総数を数え上げる事は、確率の理論でも重要です。