「乗(じょう)」は数学では掛け算の意味です。掛け算の事を「乗法(じょうほう)」とも言います。
「~を掛け算する」という意味で「~を乗する」とも言います。
2乗(自乗、平方)の意味と表記
2×2=4、3×3=9、4×4=16など、
「同じ数を掛け算する事」を「自乗」あるいは「2乗」と言います。
これを22=4、32=9、42=16のようにも書きます。
「2の2乗(自乗)イコール4」などのように読みます。
また、後に少し触れるように「平方」という言葉も「2乗」の意味で使う事があります。
文字式や関数の場合でも同じで、x2は「エックスの2乗(自乗)」もしくは「エックス2乗(自乗)」と読み、x・x(xとxとの掛け算)を表します。

2乗(自乗、平方)の応用・使われ方
正方形の面積は一辺の長さの2乗になります。
面積の単位をcm2【平方センチメートル】やm2【平方メートル】のように書くのはそのためです。
(例えば3cm2であれば、1cm2の正方形の3個分の広さ【面積】という事。)
また、円の面積は円周率と「半径の2乗」の積で表されます。
(※その公式の証明は、円周の長さの公式を半径で積分する、置換積分で計算する、微小な三角形の面積の合計と考えて「円周の長さ」×半径÷2として出す・・等の方法があります。)
そのように、面積を表すのに頻繁に使われる意味でも「2乗」というものは重要な掛け算になります。
直角三角形の斜辺の長さを表す三平方の定理も、c2=a2+b2という2乗を含む形です。
ここでの「平方」とは「2乗」の意味です。
(※実際、定理の証明の1つでは面積を使います。そこにも2乗が出てくる意味を見出せます。)
これは直交座標上の「距離」を計算するのにも使うので重要な定理です。
それらに関連して、三角比での cos2θ+sin2θ=1という公式も重要です。
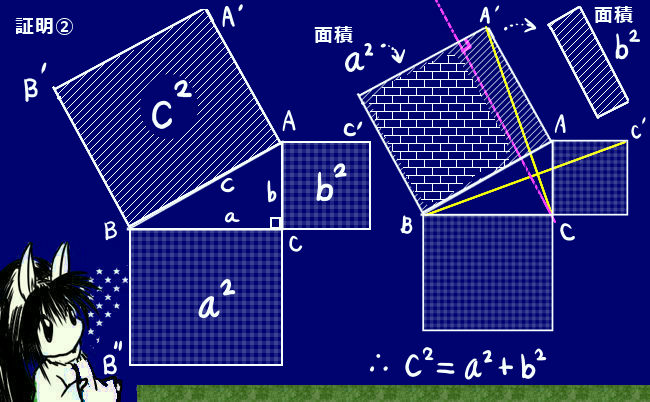
図のように、「2乗」の項が各辺の長さを持つ正方形の面積という図形的意味を持ちます。
22=4という計算に対し、逆にx2=4を満たすxの事を「4の平方根と」言います。
(※そのような平方根となるxは、+2と-2の2つが該当します。)
「2乗するとaになる数」をaの「平方根」(あるいは「2乗根」)と言います。
負の数を2乗する場合には、マイナス符号をプラス符号に変えるという計算をします。
つまり、(-1)2=+1という計算をするわけです。
【マイナスを2乗するとプラスになる理由は、それが計算の定義であるからですが、もう少し考察して説明をする事は可能です。】
つまり正の数だろうと負の数だろうと、「2乗すると正の数になる」事は確定するわけです。
(例外は0で、02=0です。また、「虚数単位」はi2=-1を満たすものとして敢えて定義します。)
そのため、絶対値を2乗する場合には単純に絶対値符号を取り払ってよいという計算になります。
|x|2=x2のように書いてよいという事です。
ax2+bx+cの形の式をxに関する「2次式」と言います。
その中のax2の部分の事を「2次の項(=『xが2乗の形になっている項』)」と呼ぶ事もあります。ax2+bx+c=0という形の方程式は「2次方程式」です。


一般のベキ乗(累乗)と指数
同じ数を「3回掛け算する」事は「3乗」すると言います。
つまり、2×2×2=8、3×3×3=27、4×4×4=64などの事であり、
それらを23=8、33=27、43=64のように表記します。
サイコロのような立方体の体積は「一辺の長さの3乗」で表されます。
それに由来して、単位の体積はm3【立方メートル】やcm3【立方センチメートル】で表記します。
球の体積は半径の3乗に比例するという公式が成立します。
文字式等に対しても、r3=r・r・r 【あるいはr×r×r】のように定義します。
4乗や5乗の場合も同じように表記します。
- 24=2×2×2×2=16 【2の4乗】
- 25=2×2×2×2×2=32 【2の5乗】
このように一般的にan【nは自然数「aのn乗」】で表された数を、
aの「累乗」あるいは「ベキ乗」と呼んだりもします。
xn=aを満たすxを、aの「n乗根」と言い、
そのようなn乗根一般の事を「累乗根」「ベキ乗根」と呼ぶ事もあります。
例えばx3=5を満たすxは「5の3乗根」と呼ばれます。
無限級数展開のうち、xnの形の項が続くものを特に「ベキ級数展開」と呼ぶ事もあります。
$$例えば e^x=1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\cdots 等です。$$
◆この例はマクローリン展開。
◆「累(るい)」とは「重なり」「次々に重ねる事」を表す漢字です。
一般には「累積(るいせき)」や「累家(るいか。代々続いてきた家)」のような語で使われます。【野球の「ベース」は「塁」なので区別注意。】
「ベキ」については漢字では「冪」をあてます。
「冪」とは元々は「食物を覆う布」の事を意味します。
x2やx3のようなxnの形の単独の式(関数)は「単項式」と呼ぶ事があります。
それらの係数倍を加え合わせた式は「多項式」と呼ばれます。
- 単項式:x2、x3、x4、xn
- 多項式:1+2x【1次式】、1+x+3x2【2次式】、1+x+x3【3次式】
(これらはxの関数とみなす場合には「1次関数」「2次関数」「3次関数」のようにも呼ばれます。)
1+x+x3 =0のような形の方程式は「3次方程式」です。
1+2x+x3+x4 =0のように、4次の項を含む方程式は「4次方程式」です。
anxn+an-1xn-1+an-2xn-2+・・・+a2x2+ax+a=0の形の方程式は
「n次方程式」であり、そのようなn次方程式一般を「多項方程式」と呼びます。
xaというベキ乗の形の単項式に対して、aの部分を「指数」と呼びます。
例えばx3の指数は3であり、x5の指数は5であるといった具合になります。
この「指数」の部分は、数学的には実は自然数でなくてもよく、実数なら何でもあてる事ができます。【また、定義をきちんとすれば複素数を代入する事もできます。(複素数の指数関数表示)】
指数を全実数の範囲とする時には、次のような定義が行われます。$$x^0=1,\hspace{10pt}x^{-n}=\frac{1}{x^n},\hspace{10pt}x^{\large{\frac{1}{n}}}=^n\sqrt{x}【xのn乗根のうち正の数のもの】$$このような定義をすると、「正の数 x に対して \(x^a\)≦\(x^b\) ならば\(a≦b\)である」という関係が成立します。
指数として無理数を代入する時も、その関係式が成立するようになっています。
$$そのため、例えばx>0に対してx^3<x^{\pi}<x^{3.2}などが成立します。$$
単項式や多項式の場合と違って、ある数の指数の部分が変数になっているものは指数関数と呼ばれます。(高校の初等関数の1つ。指数関数は対数関数と対になっていて、互いに逆関数の関係にあります。)
それは例えば、2x【2のx乗】やex【eは「自然対数の底」】といった関数であり、高校数学(特に微積分)や理工系の大学の学問でも重要な関数です。
