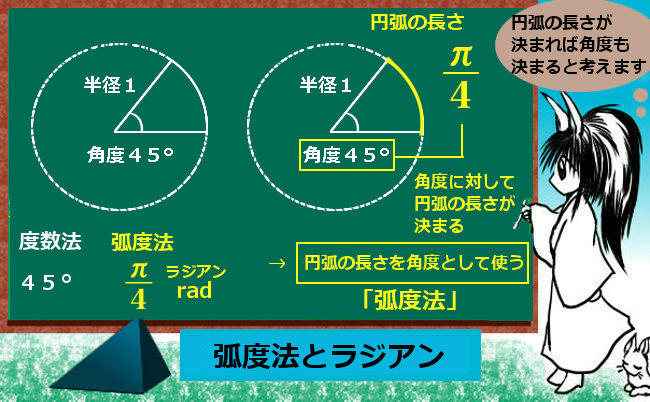
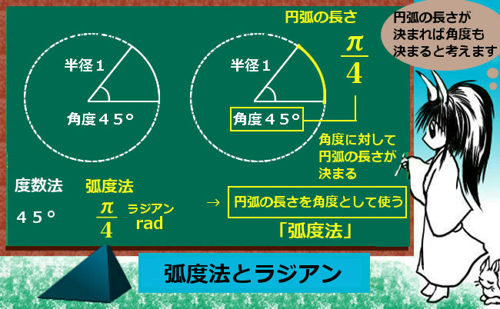
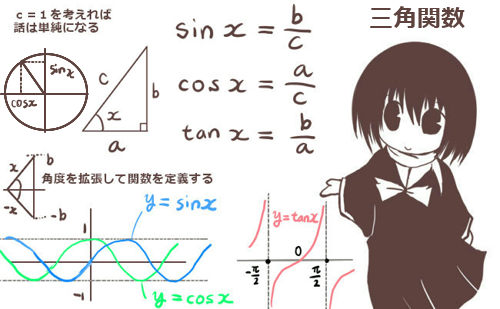
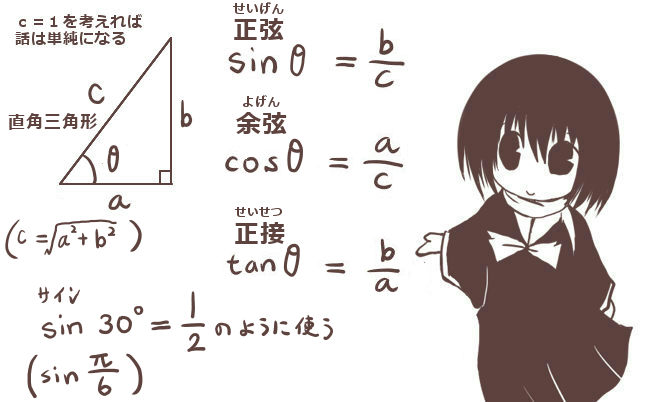
三角関数とは、図形上の三角比 である正弦、余弦、正接の角度部分を拡張して定義域を実数全体に広げた正弦関数 、余弦関数 、正接関数 を言います。(正接関数は \(\pi\)/2の奇数倍を定義域から除きます。 )弧度法 で表します。(※度数法のまま三角関数を扱っても支障はない場合も多くあります。ただし微積分を扱う時には特に問題が発生するので注意も必要です。)
表記方法自体は三角比の場合と同じで、変数部分の記号としてxを使う事が多いです。
三角関数は、代表的な周期関数の1つでもあります。これは、同じ関数の値が等間隔の変数ごとに繰り返し現れるというもので、「1回転」\(2\pi\) ごとの周期性を示します。(比例係数を使う事で、その他の値の周期とする事もできます。)
指数関数や対数関数と同じく、高校で扱われる重要な関数である初等関数 の1つです。
三角比との違いは、数学的に厳密な違いが定義されているわけではありませんが、三角比というのはどちらかというと平面の図形に対して0°~180°の範囲で適用するものであって、三角関数は図形問題というよりは周期関数としての性質を強調して使う事が多いです。
定義域の拡張・・角度を拡張する
三角関数の考え方は大体において三角比と同じ考え方を適用できますが、正弦関数等の変数は実数全体です。この場合、単純な直角三角形の角度としては変になる場合はどのように解釈するのか?を説明します。
■ 「0度」と負の角度 ■ \(\pi\)/2【90°】以上の角度 ■ 2\(\pi\)【360°】以上の角度【周期性】
「0度」と負の角度
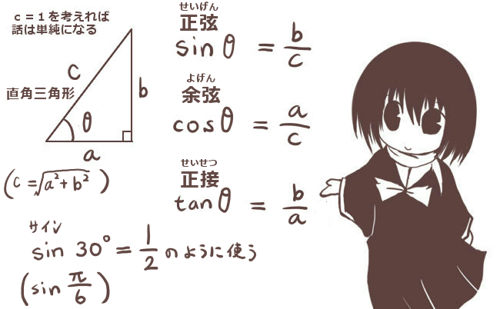
直角三角形の直角以外の部分の角度は、「もちろん0°より大きく90°より小さい範囲」です。
まず変数が0以下の場合はどうするのでしょうか?結論を言うと次のようにします。
変数が0以下の場合の三角関数
sin 0 = 0, sin(-x)=-sinx と定義する。
cos 0 = 1, cos(-x)= cosx と定義する。
tan 0 = 0, tan(-x)=-tanx となる。【tanx=(sinx)/(cosx)と定義するため。】
ここでx>0であれば-xは負の値で、x<0であれば-xは正の値です。
これは図で言うと、三角形を底辺に関して対照的にひっくり返したものを考えて「負の角度」としています。角度の方向にも向きを付けて、反時計回りをプラス、時計回りにはマイナスの符号をつけるという意味です。
まずx=0の場合には次のようにしていす。
角度0の場合の定義
x=0とした時の y=sin x と y=cosx の値の定義です。
正弦関数の場合:sin 0 =0 と定義する。 余弦関数の場合:cos 0 =1 と定義する。
これらは「定義」であるとしか言いようがない面もありますが、「なめらかな形の連続関数」になるような定義 としての1つの要請であるとも言えるのです。
また、周期関数になる という要請も加えると、定義の仕方も段々と限定されてくるわけです。意味としては、三角関数における「角度」の拡張の定義にはそのような意味があると捉える事ができるのです。
負の角度
ここでは表記としてはxがプラス符号であるとして、それにマイナスをつけた「-x」を負の数として扱っています。
正弦関数の場合:sin(-x)= -sinx【0から始まり-1に向けて関数の値は減少していく】 余弦関数の場合:cos(-x)= cosx【1から始まり0に向けて関数の値は減少していく】 $$例えば\hspace{10pt}\sin\left(-\frac{\pi}{4}\right)=-\sin\frac{\pi}{4}=-\frac{1}{\sqrt{2}},\hspace{10pt}\cos\left(-\frac{\pi}{4}\right)=\cos\frac{\pi}{4}=\frac{1}{\sqrt{2}}$$
正弦の場合と余弦の場合ともに、符号の関係にだけ注意すればよいという事になります。
尚、ここでは sin(-x)= -sinx において「xは正の値」を考えて変数が負の場合の説明をしましたが、
\(\pi\)/2【90°】以上の角度
では、変数がプラスの値の時に戻って、変数が\(\pi\)/2以上の場合はどうするのでしょう?
三角関数において、定義域を\(\pi\)/2以上に拡張する場合は次のようにします。
変数が\(\pi\)/2以上の場合の三角関数
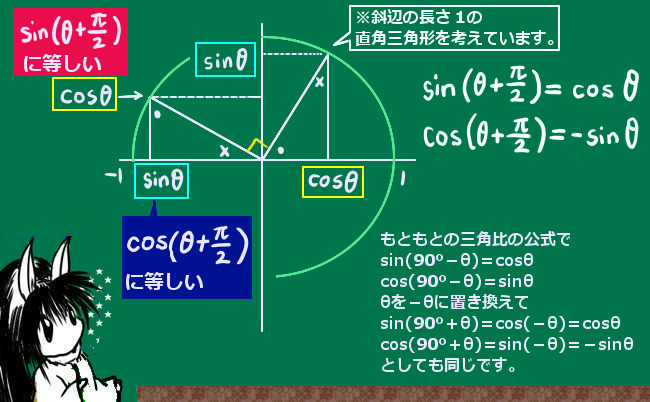
sin(\(\pi\)/2) = 1, sin(x+\(\pi\)/2)=cosx と定義する。
cos(\(\pi\)/2) = 0, cos(x+\(\pi\)/2)=-sinx と定義する。
tan \(\pi\) = 0, tan(x+\(\pi\)/2)=-1/(tanx) となる。
mを整数として tan(\(\pi\)/2+m)は、定義しない !【無限大を避けるためです。】
ここで正弦と余弦についてはxは実数のうち何の値でもよく、負の数や直角を超える値を入れたとしても整合性がとれた定義式になっています。
また、正弦関数と余弦関数については次式も成立し、これを使うと計算上便利です。
公式
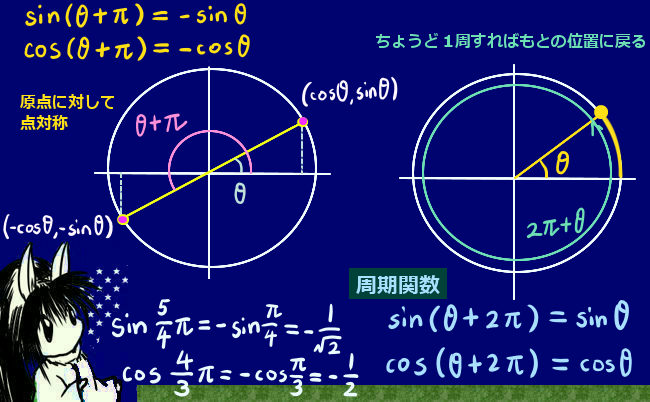
sin(x+\(\pi\))=-sinx, sin(\(\pi\)-x)=sinx
cos(x+\(\pi\))= -cosx, cos(\(\pi\)-x)=-cosx
これらは式としては統一的にまとめる事もできますが、図形的な意味としては別々に捉える事も1つの方法として便利である場合があります。正接関数についても同様の式を作る事は可能です。
さて、この定義を見ると角度が負の場合と比較して、かなり複雑であるようにも見えます。
変数が直角を考える場合には、今度は直角三角形の高さ部分の辺に関して対照的になるようにひっくり返すのです。この場合も、関数の値の絶対値は直角未満の場合の三角比の値を流用して符号だけをいじるという定義の仕方をします。
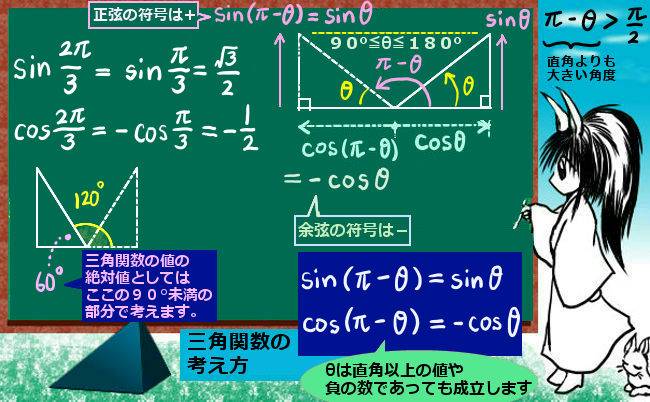
90°を超えて180°未満の「鈍角」の範囲における三角関数の具体的な値を調べる時には、鈍角を「180°-鋭角」と考えるか、「90°+鋭角」と考えるかの2通りの計算で便利なほうを使うのが普通です。
鈍角を「180°-鋭角」と捉える場合の三角関数の値の計算方法です。 鈍角を「鋭角+90°」と捉えた場合の三角関数の値の計算方法です。こちらは、通常の三角比の場合に成立する公式を利用して式変形で考える事も可能です。 尚、式として考える場合、「90°+鋭角」の鋭角部分をマイナスにしてさらに90°加算する事で
$$\sin\left(\pi-\theta\right)=\sin\left(\frac{\pi}{2}+\frac{\pi}{2}-\theta\right)=\cos\left(\frac{\pi}{2}-\theta\right)=-\sin(-\theta)=\sin\theta$$
$$\cos\left(\pi-\theta\right)=\cos\left(\frac{\pi}{2}+\frac{\pi}{2}-\theta\right)=-\sin\left(\frac{\pi}{2}-\theta\right)=-\cos(-\theta)=-\cos\theta$$
変数の値が2直角、つまり\(\pi\)の時には正弦関数の値は0、余弦関数の値は-1です。これは定義として捉えてもよいですし、上記の sin(x+\(\pi\))=-sinxから導出するという形でも同じです。これらも、意味としては関数の増減との対応・周期性・なめらかな連続性を満たす要件として考える事ができます。
さらに変数が\(\pi\)を超える場合には負の角度の時のように底辺に関して対照的にひっくり返します。この場合は、sin(x+\(\pi\))=-sinx, cos(x+\(\pi\))= -cosx の関係式を使うと把握しやすいでしょう。図を見ながら、図形的に捉えましょう。
角度が2直角を超える場合には、座標上で言う第3・第4象限に三角形を配置する形になります。この時には原点に対して点対称になる三角形を考えて符号を反転するだけと考えると計算が簡単な場合が多いでしょう。 さらに角度の値を大きくすると、今度は再び高さ部分に関してひっくり返り、座標軸上で言うと第4象限の位置に配置された三角形を考える事になります。
2\(\pi\)【360°】以上の角度【周期性】
角度を増やして、4直角、つまり360°に達し、それを超えた場合はどうなるでしょう。
この場合は、sin(x+\(\pi\))=-sinx, cos(x+\(\pi\))= -cosx の関係式の変数にもう一度 \(\pi\) を加えるのです。
すると、再度符号が反転して sin(x+2\(\pi\))=sinx, cos(x+\(\pi\))= cosx となり、
これが三角関数の周期性 と呼ばれる性質で、以降、角度をどれだけ増やしても延々と周期的に値を繰り返すという事です。これは正接関数についても成立します。
三角関数の周期性
次のように、三角関数は2\(\pi\)ごとに同じ値を繰り返します。
sin(x+2\(\pi\))= sinx
cos(x+2\(\pi\))= cosx
tan(x+2\(\pi\))= tanx
この周期性は、マイナスの向きに角度を減らした場合にも適用できます。つまりマイナス方向にもプラス方向にも、実数全体にわたって2\(\pi\)の周期性があるという事です。
sin(x+2\(\pi\))=sinxの関係から、sin(2\(\pi\)-x)=sin(-x) となり、余弦関数の場合も同様です。これは図形的に見ると、同一の頂点に相当する部分に至る角度を反時計回り(プラス)で測っても時計回り(マイナス)で測っても三角関数の値は同じである事を意味します。
尚、sin2xのような関数を考える場合には、周期性は sin(2x+2\(\pi\))=sin2xのようになります。
単位円による定義方法
さて、以上の三角関数の定義と性質を見ると、式だけで覚えるのは大変複雑で、図形的に見るとそれほど難しい理屈ではない事が分かると思います。
上記の図でもところどころに描いていますが、じつは三角関数を把握するには円を描くと便利です。(三角関数の別名を「円関数」とも言います。)
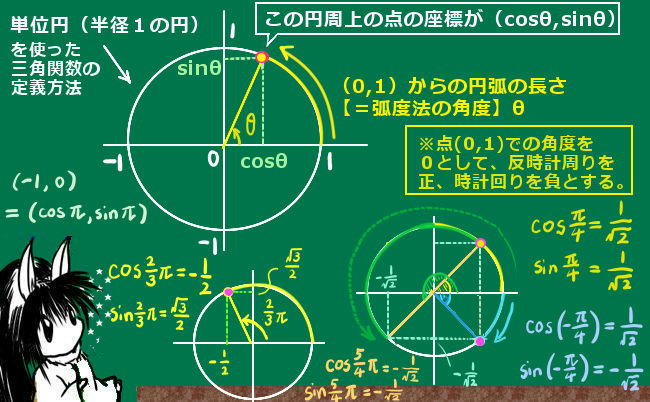
この円は、原点を中心とした半径を1にした円で、単位円 と呼ばれます。
すると、斜辺の長さに相当する「半径」が1ですから、角度の取り方は前述の方法と同じであるとすると、
この単位円による方法でも適切に三角関数の値を出せるので、これを定義にしてしまうやり方もあります。
単位円による三角関数の定義
直交座標上の原点を中心とする半径1の円周上の点(X,Y)を考えて、
X=cosx すなわち余弦関数と定義する
Y=sinx すなわち正弦関数と定義する 正接関数は tanx=(sinx)/(cosx) で定義する 各三角関数には2\(\pi\)の周期性があり、
単純な覚えやすさと使いやすさに関しては、この単位円による方法は非常に優れています。
欠点があるとすれば、三角比の拡張として唐突に「円」を持ち出すと、やはり少しばかり飛躍を感じさせるのも事実だと思います。最初から単位円による定義で教え込まれてしまうと結局「わけもわからずに」暗記するだけ・・という事になりがちです。
単位円を使った三角関数の定義は、覚え方や計算の便宜としては非常に優れています。 重要な公式まとめ
三角関数の公式としては、簡単に4つのグループに分けると次のようなものがあります。
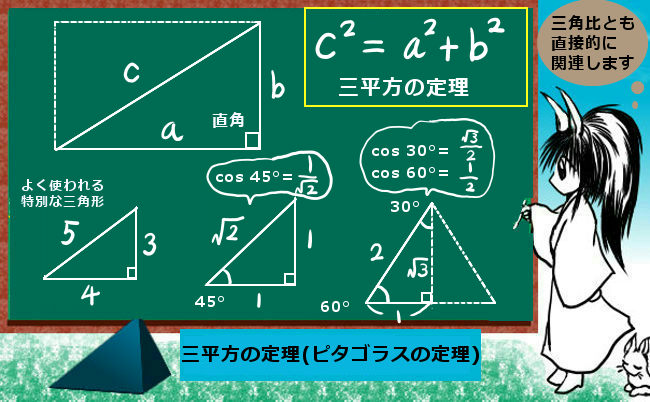
三角比についても適用できる公式 定義域を拡張した三角関数に特有なもの(例えば周期性) 正弦定理と余弦定理 加法定理と、それから派生する公式 まず、三角比についても成立するいくつかの公式は、三角関数でも成立します。これは三角比範囲の角度でのみ成立するのではなく、負の角度や直角以上の角度を代入してもきちんと成立するところが便利です。
三角関数の公式①
次式は三角比について成立しますが、
これらの証明 は三角比の説明のところで詳しく記しています。
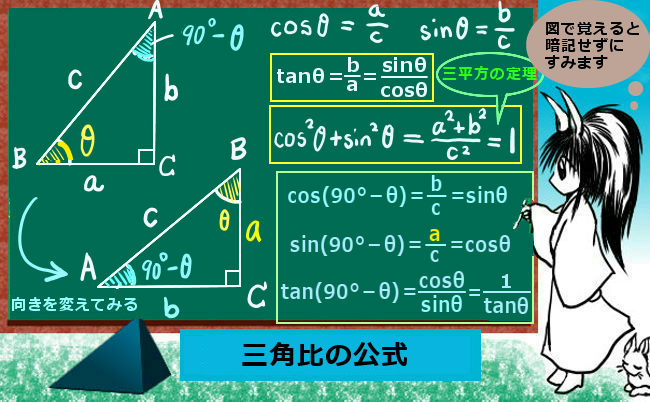
周期性も含めて、三角関数特有の公式・性質も整理しておきましょう。
三角関数の公式②
これらは特に三角関数において成立する関係式です。
$$\cos \left(\frac{\pi}{2}+ x\right)=-\sin x$$
$$\sin \left(\frac{\pi}{2}+ x\right)=\cos x$$
$$\sin(-x)=-\sin x\hspace{20pt}\cos(-x)=\cos x$$
$$\sin(\pi +x)=-\sin x\hspace{20pt}\cos(\pi +x)=-\cos x$$
$$\sin(\pi -x)=\sin x\hspace{20pt}\cos(\pi -x)=-\cos x$$
$$\sin(2\pi +x)=\sin x\hspace{20pt}\cos(2\pi +x)=\cos x$$
最後の関係式については周期性と呼ばれる事は前述した通りです。
図形的に三角形に対して成立する公式で三角関数を使うものには、正弦定理 と余弦定理 というものがあります。(余弦定理のほうがどちらかというと重要かと思います。)それらは基本的には三角比に対して成立しますが、角度として鈍角や直角を適用する場合には三角関数の定義を使用すると図形的な対応もうまくとれるという具合になります。図形的な対応さえきちんとつけるなら、余弦定理に関しては全実数の範囲の角度を適用しても成立します。
三角関数の公式③ 図形的な定理
正弦定理:三角形の辺a、b、cの対角の大きさをそれぞれA,B、C、三角形に外接する円の半径をRとすると
余弦定理:三角形の辺a、b、cと、辺aの対角の大きさAについて次の関係が成立する。2 =b2 +c2 -2bccosA
また、三角関数の加法定理 というものがあって、これは複素数 の理論の一部を構成しており、微積分のほうで計算を進めるために使う事もあるので三角関数の公式の中では重要な部類に入ります。積和の公式・和積の公式・倍角の公式 と呼ばれるものもあります。それらは本質的にはもともと加法定理そのもので、少し式変形をして形を変えたものになります。
三角関数の公式④ 加法定理
2つの角度の大きさ A, B に関して次式が成立します。
sin(A+B)=sinAcosB+cosAsinB
sin(A-B)=sinAcosB-cosAsinB
cos(A+B)=cosAcosB-sinAsinB
cos(A-B)=cosAcosB+sinAsinB
sinAcosB などは、sinA と cosB の積です。
正接関数についても、tan(A+B)=sin(A+B)/cos(A+B) の計算によって加法定理の公式を作る事が可能です。
この他に、高校数学では必要ありませんが、三角関数を使った無限級数 によって周期関数を解析する技法があります。そこでも三角関数の基本的な性質や公式は前提として話が進められる事も多いので、基礎事項をよく知っておくと後々の学習が進めやすい事もあろうかと思います。