投稿者: 恭平

３次方程式の「解の公式」の導出方法について説明します。「公式」の導出は、２段階に分けて行います。

一見複雑に見える箇所もあるかもしれませんが、必要な知識は基本的には中学～高校数学程度の式変形です。

①３次方程式の２次の項を、変数の置き換えで消去する

まず、任意の３次方程式は、変数の置き換えによって、ある特別な形の３次方程式に「必ず」変形できる事を示します。（「必ず」というのがポイントです。）

３次の項の係数はそれで式の両辺を割って１にできるのでその後の事を考えます。

$$x^3+ax^2+bx+c=0$$は変数の置き換えにより必ず$$X^3+Ax=B$$の形変形できる。

要するに「２次の項は必ず消せる」という意味です。

x = X + C とします。X に関しても３次方程式になるという形を保つために、X は x に関する一次式である必要があります。

$$x^3=X^3+3X^2C+3XC^2+C^3,\hspace{10pt}ax^2=a(X^2+2XC+C^2) ,\hspace{10pt} bx=b(X+C)$$

２次の項の係数が０であるとすると、

$$3C+a=0\Leftrightarrow C=-\frac{a}{3}$$

とおけば成立します。

$$x^3+ax^2+bx+c=0, \hspace{10pt} x= X-\frac{a}{3} とすると、$$

$$ \left(X-\frac{a}{3}\right) ^3+a \left(X-\frac{a}{3}\right) ^2+b \left(X-\frac{a}{3}\right) +c=0$$

$$ \left(X^3-X^2a+X \frac{a^2}{3}- \frac{a^3}{27} \right) +a \left(X^2-X\frac{2a}{3}+ \frac{a^2}{9} \right) +b \left(X-\frac{a}{3}\right) +c=0$$

$$X^3+X \left( -\frac{a^2}{3}+b \right)+ \frac{2a^3}{27}-\frac{ab}{3} +c=0 $$

ここで、Ｘに関する係数部分がごちゃごちゃしてるので別の記号ＡとＢで表します。

$$ A=-\frac{a^2}{3} +b , \hspace{10pt} B= -\frac{2a^3}{27} +\frac{ab}{3} -c $$

このように置く事で、

$$X^3+Ax=B$$

の形として方程式を考察できるわけです。

② ３乗の展開式を利用して、解く

さてしかし、この形にしたからといってうまく「解ける」のかという話になります。

これは、じつは３乗に関する展開式についての簡単な式変形によって解く事ができます。

任意の２つの実数（複素数でも可）Ｔ，Ｕに対して

$$(T-U)^3=T^3-3T^2U+3TU^2-U^3$$

$$\Leftrightarrow (T-U)^3+3TU(T-U)=T^3-U^3 $$

この式は、恒等式です。つまり、いつでも成立している関係式です。

これは一体何を意味するのでしょうか？
これは、「次の関係が成立すれば」左辺と右辺が必ず等しくなるわけですから「方程式が成立する」という事です。

$$X=T-U$$

$$A=3TU$$

$$B=T^3-U^3$$

すなわち、これらの関係を満たす X が３次方程式の解になるという事なのです。

もっと具体的には、ＴとＵをＡとＢだけで表し、Ｘ＝Ｔ－Ｕに代入すれば ＸをＡとＢだけで表せて、それによっておおもとの x が係数 a, b, c のみで表せる・・つまり「解の公式」が得られる、というパズルです。

しかし、上の式を見るとＢとＴ、Ｕの関係には３乗が入ってます。３次方程式の解の公式が得られていない条件でこれをうまく解けるのかというと、じつは解けます。

$$U=\frac{A}{3T}$$

$$B=T^3-\frac{A^3}{27T^3}$$

$$\Leftrightarrow (T^3)^2-B(T^3)-\frac{A^3}{27}=0$$

このように、「『Ｔの３乗』の２次方程式」ができるので、これは（無理やり）解く事ができるのです。

結果は、次のようになります。

$$T^3=\frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}}$$

$$U^3=T^3-B= -\frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}}$$

$$X=T-U= \hspace{5pt} ^3\sqrt{ \frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}} }- \hspace{5pt} ^3\sqrt{ -\frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}} }$$

$$x= X-\frac{a}{3}= \hspace{5pt}^3\sqrt{ \frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}} }- \hspace{5pt} ^3\sqrt{ -\frac{B}{2}\pm \sqrt{\frac{B^2}{4}+\frac{A^3}{27}} } -\frac{a}{3} $$

ただし、ここでの３乗根の記号は複素数の範囲も含めた３つの数を取りえるものとします。３次方程式は、複素数範囲まで考え、重解を２解と数えると必ず３解を持ちます。 その事が、３乗根によっても表現されるわけです。

３次方程式の解の公式を知る意味：数学史的な価値

さて、このようにして「解ける」事は確かに言えるわけですが、色々置き換えがあって、公式としては代入するだけでもすごく面倒ですね。そういうわけで、物理や工学で仮に３次方程式を解く場面があったとしても、できる事ならこの公式使いたくないわけです。実質的には「手計算で解くなら２次方程式まで」と、基本的には思ってよい理由です。

このように、公式が存在する事と、それが応用の場面等で使いやすいものか・便利なものかという事は、別問題である事もあるわけです。

では、純粋数学的に考察した場合はどうかというと、この３次方程式の解法は、４次方程式については似た事ができます。しかし、５次以降は使えないのです。つまり、「３次や４次については適用できる」という特別なものになります。多項方程式について純粋数学的に一般的に考察する時は、より抽象的な考察が必要であるという事です。

この３次方程式の「解の公式」の解法の話は、大学数学においてはむしろ数学史の中で扱われる事が多いです。というのも、西欧で「複素数」というものが考察されるきっかけになったのがこの３次方程式の解法であると言われているからです。（※２次方程式ではなく３次方程式の解法というところに、数学史的に指摘しておくべきポイントがあるという事です。）

ちなみに数学史的には、この３次方程式の解の公式が「発見」されたのは１６世紀という意外に遅い時期であり、しかし４次方程式の解の公式はその後に割とすぐ見つけられて、その後「５次方程式の解を一般的に係数のベキ根によって表す事はできない」という事が示されたのは１９世紀まで飛びます。
歴史というか数学の研究史としては、そのような事も１つの教養的知識として多少知っておいてもよいのではないかと思います。

また、数学史的な事についてもう１点補足しますと、１６世紀に「解の公式」が見出された時には、解法の流れは上記の方法と同じですが考え方として別の考察の仕方をしていました。それは、上記のように式を展開して関係式を導出するよりも、図形的な考察から関係式を導出していたという点です。

この場合、図形は図形でも、平面図ではなく立体の体積に関する考察です。立体ですから、体積に関して３乗を使うというわけです。参考までに、次図を記しておきます。

中学でも高校でも２次方程式の「解の公式」は嫌われものだと思いますが、実際、決してきれいな形ではなく覚えやすい部類の公式でもないでしょう。

暗記できる人は暗記してもらって構わないと思いますが、ここでは「暗記しなくても解を出せる」方法を述べます。

数学的にも応用的にも、２次方程式の位置付けは「比較的簡単な操作で解を出せる」というものでしょう。

３次方程式の解の公式も存在しますが、これは２次方程式の場合よりもさらも面倒な形で、応用の場面で手計算で使う事は、基本的にほとんど無いのではないかと思います。

つまり、ｎ次方程式の中で、「手計算で比較的簡単に解ける」ものの限界が２次方程式なのです。できる事なら１次方程式が最も簡単ですが、２次方程式までなら手計算でもじゅうぶん何とかなる、という事なのです。（もちろん。高次の方程式でも容易に因数分解できるようなものであれば手計算で解を出せます。）

解の公式の導出

２次方程式の解を公式として表せる根拠は、一般の２次方程式を加減乗除と累乗の計算によって必ず次の形

$$X^2=C$$

に変形できる事にあります。（同様の操作は３次・４次方程式だと少し面倒で、５次以上になると一般の方程式に対して統一的にそのような操作を行う事はできません。）

$$ax^2+bx+c=0$$

において、本当に大事な事は x = ・・の公式を丸暗記する事ではなく、これを容易に式変形できる事です。

まず、次のように変形します。a はゼロではないとします。

$$a\left(x^2+\frac{b}{a}x\right)+c=0$$

次の変形は少しややこしいと思う人もいるかもしれませんが、これを容易に計算できる事が、中学・高校数学では非常に大事です。

$$a \left (x+\frac{b}{2a} \right )^2-a \left ( \frac{b}{2a} \right )^2+c=0$$

$$\Leftrightarrow a \left (x+\frac{b}{2a} \right )^2 =a \left ( \frac{b}{2a} \right )^2 -c$$

$$\Leftrightarrow \left (x+\frac{b}{2a} \right )^2 = \left (\frac{b}{2a} \right )^2 – \frac{c}{a} =\frac{b^2}{4a^2} -\frac{c}{a} =\frac{b^2 – 4ac }{4a^2}$$

$$ \Leftrightarrow x+\frac{b}{2a} =\pm \frac{\sqrt{ b^2 – 4ac }}{2a} $$

$$ \Leftrightarrow x= \frac{-b\pm \sqrt{ b^2 – 4ac }}{2a} $$

これで、「解の公式」になっていますね。

この計算を、具体的な問題を試験で出されるたびに行うのはかえって大変ではないかと思う人もいると思います。しかし、上記は一般の係数 a, b, c でやっているから少し面倒であるわけで、具体的な数値が係数として与えられている場合にはもっと簡単になります。

具体的な計算問題を解いてみる

具体的な問題を見てみましょう。

$$x^2+7x+11=0$$

もしかすると手計算で因数分解できるかもしれませんが、変形で解いてみましょう。

$$ x^2+7x+11=0 $$

$$ \Leftrightarrow \left(x+\frac{7}{2}\right)^2-\frac{49}{4}+11=0$$

$$ \Leftrightarrow \left(x+\frac{7}{2}\right)^2=\frac{5}{4} \Leftrightarrow \left(x+\frac{7}{2}\right) =\pm \frac{\sqrt{5}}{2}\Leftrightarrow x= \frac{-7\pm \sqrt{5}}{2}$$

もちろん、結果は解の公式を使った場合と同じです。途中の分数計算を手早く済ませる必要は確かにありますが、それさえできれば公式そのものを覚えていなくてもかなり早く解答を出せるはずです。

まとめと学ぶ意味

大学数学や物理でも２次方程式を解く場合があります。しかし、そんなにやたらと多く出てくるものではなく、時々、ポッと出てくるようなものです。

そういう時には、中学や高校で教わった公式を明確に覚えている人もいるかもしれませんが、忘れているか曖昧になる人も多いのではないかと思います。そうした場合には、公式を探し出して係数を当てはめるよりは、上記の式変形の方法で自分で解いてしまったほうが多分早いでしょう。

前述の通り、「手計算で簡単に解ける多項方程式は基本的にｎ＝２の時まで」という事が重要です。（３次・４次の方程式の解の公式は、あまり使わないです。）大学数学の代数学では、より抽象的・一般的な視点から多項方程式の解について考察したりします。また、どうしても高次の多項方程式を解く必要になる場合には手計算で解く事は放棄して、コンピュータによる数値計算を行います。

このページでは、高校数学程度の行列の知識のうち、特定の種類の行列の呼び名について説明します。

数学で言う行列の定義と行列の演算（足し算、引き算、掛け算）については別途にまとめています。

行列は、行と列の数がそろっているものに限りませんが、多くの行列の用語は行と列の数が等しい正方行列に対してのものが多いです。そのため、このページで扱う行列の多くは正方行列になります。

$$例：３次の正方行列\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) $$

★ 正方行列の行の数（＝列の数）をｎとする時、その正方行列をｎ次の正方行列と呼ぶ事があります。例えば３×３行列は、３次の正方行列です。

★ 行列の中の各数値等を成分と言い、ｍ行ｎ列目の箇所にある成分を（ｍ,ｎ）成分などと言ったりします。

単位行列・零行列・対角行列

ここでは、行列は正方行列とします。

まずは簡単なものから見ていきましょう。

■ 単位行列　■ 零行列（ゼロ行列）　■ 対角行列
■ 参考：虚数単位の行列表現

単位行列

まず、これは簡単です。ある行列Ａに掛け算をした時に、掛け算の結果がＡそのものになる行列を単位行列と言います。通常の掛け算で言う１に相当します。

★ 多くの場合、単位行列はＩかＥで表します。

行列の掛け算を行えるとき、Ａ×Ｉ＝Ｉ×Ａ＝Ａが成立します。

一応ちょっとした注意点として、「行列の掛け算の定義」を何かてきとうに考えた時に、そのような「単位行列」の存在は必ずしも自明とは言えません。そのような行列が存在する事を示しておく必要があります。

もっとも、そのような単位行列は確かに存在し、次のようなものです。

$$例：３次の単位行列　I=\left(\begin{array}{ccc}
1 & 0 & 0\\
0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right) $$

このように、正方行列の「対角線」に相当するところ（これを対角成分と言います）が全て１であり、残りの成分は全て０である行列が単位行列です。何次の正方行列であっても、単位行列は「対角成分が全て１で、残りの成分は全て０」である行列として表せます。

簡単な計算例を見てみましょう。

$$\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) \left(\begin{array}{ccc}
1 & 0 & 0\\
0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right) $$

$$= \left(\begin{array}{ccc}
a_{11} \cdot 1+ a_{12} \cdot 0 + a_{13} \cdot 0& a_{11} \cdot 0+ a_{12} \cdot 1 + a_{13} \cdot 0 & a_{11} \cdot 0+ a_{12} \cdot 0 + a_{13} \cdot 1 \\
a_{21} \cdot 1+ a_{22} \cdot 0 + a_{23} \cdot 0 & a_{21} \cdot 0+ a_{22} \cdot 1 + a_{23} \cdot 0 & a_{21} \cdot 0+ a_{22} \cdot 0 + a_{23} \cdot 1 \\ a_{31} \cdot 1+ a_{32} \cdot 0 + a_{33} \cdot 0 & a_{31} \cdot 0+ a_{32} \cdot 1 + a_{33} \cdot 0 & a_{31} \cdot 0+ a_{32} \cdot 0 + a_{33} \cdot 1 \end{array}\right) $$

$$= \left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) $$

掛け算の順番を入れ替えてＩ×Ａを計算しても同様の結果になります。

一般の行列の掛け算では、Ａ×Ｂは、ものによってＢ×Ａに等しくなる事もあるし、等しくない事もあります。

零行列（ゼロ行列）

零行列とは、行列の全ての要素が０である行列です。これは正方行列でなくてもそのような行列は当然あり得ますが、通常は正方行列を考えます。

★ 零行列の記号は、Ｏ（アルファベットの「オー」）で表す事が多いです。

例えば３次の零行列は、次の通りです。

$$例：３次の零行列　Ｏ=\left(\begin{array}{ccc}
0 & 0 & 0\\
0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right) $$

零行列については、行列の演算の方法さえ知っていればすぐに分かるかとは思いますが、
Ａ＋Ｏ＝Ａ、Ａ－Ｏ＝Ａ、Ａ×Ｏ＝Ｏ×Ａ＝Ｏが成立します。

少し気を付ける必要があるのは、行列の場合は仮に２つの行列の掛け算の結果が零行列だったとしても、もとの行列のいずれも零行列だとは限らないという事です。

簡単な例として２次の正方行列で、零行列でない２つの行列の掛け算が零行列になる場合を挙げておきます。

$$ \left(\begin{array}{cc}
1& 0 \\
0& 0 \end{array}\right) \left(\begin{array}{cc}
0& 0 \\
0 & 1 \end{array}\right)= \left(\begin{array}{cc}
1\cdot 0+0 \cdot 0& 1 \cdot 0+0 \cdot 1 \\
0 \cdot 0+0 \cdot 0 & 0 \cdot 0+0 \cdot 1 \end{array}\right)=O $$

通常の実数などであれば、ab = 0 ⇒ a = 0 または b = 0 が成立します。
行列の場合にはこの関係が成立しないという事です。

対角行列

単位行列のように対角成分以外の成分は全て０で、対角成分に何らかの数（全て１とか全て０の場合を除く）があるものを対角行列と言います。

これは、具体的には様々なものがあり、総称として対角行列と呼びます。

$$３次の対角行列の例：　\left(\begin{array}{ccc}
2 & 0 & 0\\
0 & -1 & 0 \\ 0 & 0 & 4\end{array}\right) $$

この形の行列は、もちろん通常の行列よりも計算が簡単になります。

参考：虚数単位の行列表現

それほど重要ではないので参考程度に述べますが、虚数単位 i に相当する行列も存在します。これを、虚数単位の行列表現と呼ぶ事があります。どういうものかというと、２乗すると単位行列の「－１」倍になる行列という意味です。

$$虚数単位の行列表現：A×A=A^2=-1 を満たすA$$

具体的にはどういうものかというと、２次の正方行列では次のようなものです。

$$A= \left(\begin{array}{cc}
0& 1 \\
-1 & 0 \end{array}\right) $$

試しに２乗を計算してみると、次のようになります。

$$ \left(\begin{array}{cc}
0& 1 \\
-1 & 0 \end{array}\right) \left(\begin{array}{cc}
0& 1 \\
-1 & 0 \end{array}\right) = \left(\begin{array}{cc}
0\cdot 0+ 1\cdot -1 & 0\cdot 1+ 1\cdot 0 \\
-1\cdot 0+ 0\cdot -1 & -1\cdot 1+ 0\cdot 0 \end{array}\right) = \left(\begin{array}{cc}
-1&0 \\
0 & -1 \end{array}\right) =- I $$

関連する事項としては「回転行列」というものがあります。２次の正方行列の要素に三角関数を上手に配置するとうまい具合に加法定理の形になり、「回転」を表せる事に関係します。複素数を極形式で表すと虚数単位 i は複素平面上で「９０°回転」を表せるわけですが、その対応として上記の虚数単位に対応する２次の正方行列も回転行列としては９０°回転を表すものです。

$$回転行列： \left(\begin{array}{cc}
\cos \theta&\sin \theta \\
-\sin \theta & \cos \theta \end{array}\right) $$

この回転行列で角度部分が９０°の時を考えて２乗すれば加法定理によりうまい具合に１８０°になり、行列としては – Ｉ になります。

転置行列・対称行列

続いて、色々な種類の行列を見ていきましょう。

分かりにくい時には具体的な数値を入れてみた行列を考えるとよいと思います。

■ 転置行列　■ 対称行列　■ 交代行列と直交行列　

転置行列

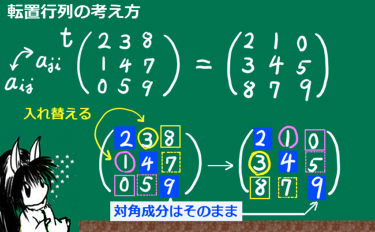
ある正方行列の（ｍ,ｎ）成分と、（ｎ, ｍ）成分を全て入れ替えた行列を転置行列(transposed matrix)と言います。ある行列と、その行列の対角成分は全て同じです。

★記号は、行列の左肩にｔの文字を書いて表される事が多いです。

３次の場合の例を記すと、次のようになります。

$$A=\left (\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right),\hspace{10pt} ^tA = \left(\begin{array}{ccc}
a_{11} & a_{21} & a_{31}\\
a _{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33}\end{array}\right) $$

$$B=\left(\begin{array}{ccc}
1 & 0& 3\\
2& 4 & -1\\ -2 & 0 & 1\end{array}\right) ,\hspace{10pt} ^tB = \left(\begin{array}{ccc}
1 & 2 & -2\\
0 & 4 & 0 \\ 3 & -1 & 1\end{array}\right) $$

この転置行列は行列の理論の中の計算上、よく出てくるので名称と記号を設定してあります。

転置行列に関して、少し間違えやすくてしかも重要な公式として、掛け算の形の行列の転置行列を考えた時に次の公式が成立します。

行列の積の転置を考えるときには個々の行列の転置行列を掛け算すればよいという事ですが、掛け算する順番がひっくり返る事に注意が必要です。

対称行列

ある正方行列の（ｍ,ｎ）成分と（ｎ, ｍ）成分が同じである行列を対称行列と言います。

例えば次の形の行列です。

$$\left(\begin{array}{ccc}
a_{11} & a & b\\
a & a_{22} & c \\ b & c & a_{33}\end{array}\right)$$

この形の行列も対角行列などと同じく計算が簡単になるので、理論で好んで使われます。

対称行列は、転置行列がもとの行列に等しいものとしても表せます。

$$対称行列の別の表し方：^tA=A を満たす行列$$

交代行列と直交行列

交代行列とは、転置行列がもとの行列の－１倍になる行列です。この行列も、そのような性質を満たす色々な行列の総称ですが、対角成分は全て０になるという特徴があります。

$$交代行列の定義：^tA=-Aを満たす行列$$

同じく転置行列を使って定義される行列として、直交行列があります。これは、もとの行列と転置行列を掛け算すると単位行列になるというものです。これに関しては、掛け算の順序を入れ替えても同じく単位行列になるという条件がつきます。

$$直交行列の定義：(^tA)A=A(^tA)=Iを満たす行列$$

複素行列

行列の成分として複素数も許容するものを複素行列と言い、なおかつ正方行列の場合は複素正方行列などと呼ばれたりします。

これは、高校の範囲では問題として問われたとしても単なる計算問題なのでさほど重要でないと思いますが、物理の量子力学では行列と複素数の両方を考える都合上、このタイプの行列を一応理論上扱う事になります。そのため、物理を学ぶのであれば後々のために知っておいたほうがよいものです。

いくつか重要な用語としての行列の名称を挙げておきます。

■ 複素共役行列　■ 随伴行列　■ エルミート行列・ユニタリ行列・正規行列　

複素共役行列

ある複素行列に対して、成分を全て共役複素数にしたものを複素共役行列と呼びます。

記号は、通常の複素数の共役と同様に、文字の上にバーを添えます。

$$A= \left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a _{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) \hspace{10pt}\overline{A}= \left(\begin{array}{ccc}
\overline {a_{11}} & \overline {a_{12}} & \overline {a_{13}}\\
\overline {a _{21}} & \overline {a_{22}} & \overline {a_{23}} \\ \overline {a_{31}} & \overline {a_{32}} & \overline {a_{33}}\end{array}\right) $$

手でノートに書くといちいち面倒ですが、意味は難しくないと思います。

随伴行列

複素正方行列に対して、共役と転置を両方考えたものを随伴行列と言います。これは、全て要素を共役にして、（ｍ,ｎ）成分を（ｎ,ｍ）成分と入れ替えるという事です。

随伴行列を表す記号は、行列の右肩にアスタリスク＊を添えて表す事が多いです。

$$複素正方行列Ａの随伴行列：A^*=^t(\overline{A})$$

エルミート行列・ユニタリ行列・正規行列

随伴行列を使って、いくつかの行列の名称が定義されます。

$$エルミート行列： A^*= Aを満たす行列$$

$$歪エルミート行列： A^*= -Aを満たす行列$$

$$ユニタリ行列： A \hspace{3pt}A ^* = A ^* \hspace{2pt} A= Iを満たす行列$$

$$正規行列： A \hspace{3pt}A ^* = A ^* \hspace{2pt} A を満たす行列$$

定義から、ユニタリ行列は全て正規行列です。
エルミート行列は、エルミット行列などと書かれる事もあり、日本語表記だと多少幅があります。

これらの行列の名称は、量子力学などで使う事があります。

逆行列と可逆行列

正方行列Ａに掛け算すると単位行列になる行列を逆行列と言います。この逆行列は、必ず存在するわけではなく、存在しない場合もあります。この逆行列が存在する行列を可逆行列と言います。

記号は、行列を「－１乗」した形として表します。ただし、「割り算」とは言わいません。あくまで、行列の積の逆演算という意味合いです。

$$正方行列A の逆行列A^{-1}：AA^{-1}=A^{-1}A=Iをみたす$$

この他に、１つの正方行列に対して決まる数値（実数や複素数）で重要なものもあります。

例えば、次の３つは数学の理論上も、物理等への応用でも重要になります。

• 行列式（デターミナント、determinant）：行列式が０でなければ正方行列は可逆行列になる
  （※一般のｎ次の正方行列の行列式の定義は少し面倒）
• 跡（トレース、trace）：正方行列の対角成分を全て合計した値。行列を群としてみなした場合の理論で使ったりする。応用だと量子化学の理論で使う事もある。
• 固有値：正方行列Ａと、列の数が１だけの行列 x（列ベクトルと言います）を使って、Ax = cx を満たす値（実数、複素数）c が存在する時、この c を A の固有値と言う。量子力学でこのタイプの関係式を扱う事があります。

このページでは「行列」について、高校で教わる内容程度の基礎知識を記します。この知識自体は大学数学や物理等への応用でも使用します。

数学で言う「行列」とは？

行列（英：matrix）は、次のように数を並べたものであって、
後述する所定の計算規則を行う事ができるものを指します。

$$\left(\begin{array}{ccc} 3 & 1 & 4\\ 1 & 2 & 0\\ 5 & 0 & -1\end{array}\right) $$

この「行列」には横方向に３つ、縦方向に３つ数が並んでいるので、
「３×３行列」あるいは「（３，３）型行列」と呼ばれる種類の行列です。

上から何個目かを示す段を行（row）と言い、
左から何個目かを示す段を列（column）と言います。
上記の行列は、３つの「行」と３つの「列」がある行列です。

行と列が必ず３ずつである必要はなく、２つずつとか４つずつでも、いくつずつでもいいですし、行と列の数が違っていても構いません。

例えば次の行列は２×２行列、４×４行列です。
このようにn×nの形である行列を、特に「正方行列」と言います。

$$\left(\begin{array}{cc} 1 & 2 \\ 5 & 0 \end{array}\right) \hspace{10pt} \left(\begin{array}{cccc} 3 & 1 & 4 & 1\\ 1 & 2 & 0 & 0\\ 5 & 0 & -1 & 1\\ 3 & 1 & 4 & 2\end{array}\right) $$

行と列の数が違う場合は、「行の数」×「列の数」の順番で「２×３行列」「（２,３）型行列」などと表記します。例えば次のようになります。

$$\left(\begin{array}{ccc}
1 & 2 & 0\\
5 & 0 & -1\end{array}\right)$$

行列自体を、１つの文字で表記する事もよくあります。この場合、別に何の文字を使ってもよいのですがアルファベットの大文字（ｷｬﾋﾟﾀﾙ）を使う事が多いです。例えば次のように書いたりします。

$$A=\left(\begin{array}{cc} 1 & 2 \\ 5 & 0 \end{array}\right) \hspace{10pt} B=\left(\begin{array}{cccc} 3 & 1 & 4 & 1\\ 1 & 2 & 0 & 0\\ 5 & 0 & -1 & 1\\ 3 & 1 & 4 & 2\end{array}\right) \hspace{10pt} Y=\left(\begin{array}{ccc} 3 & 1 & 4\\ 1 & 2 & 0\\ 5 & 0 & -1\end{array}\right)$$

ここでの例では具体的な数を入れていますが、変数を入れても構いません。
例えばてきとうに、次のような行列を考える事もできます。

$$X=\left(\begin{array}{ccc} x & 1 & 4\\ 1 & y & 0\\ 5 & x & z+1\end{array}\right) $$

行列の演算・・足し算、引き算、割り算

次に、行列同士の演算です。

行列の演算には次の３つがあります。特に重要なのは行列同士の掛け算です。

• 足し算（加法、和）
• 引き算（減法、差）
• 掛け算（乗法、積）

割り算（除法、商）はない事に注意してください。特定の行列の掛け算に対して逆の演算をできる場合もありますが、これは「逆行列」というものを掛け算するという形で行われます。

通常の数の演算のように、足し算引き算には＋、－の記号を使い、掛け算は×、・の記号を使うか２つの行列を横に並べる事で表します。

続いて具体的にどういう計算をするのかの定義です。

まず、足し算と引き算については、２つの行列の行と列の数がそろっている場合にのみ考えます。

具体的には、例えば２×３行列同士の足し算は次のようにします。

$$ \left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\end{array}\right)+ \left(\begin{array}{ccc}
b_{11} & b_{12} & b_{13}\\
b_{21} & b_{22} & b_{23}\end{array}\right) = \left(\begin{array}{ccc}
a_{11}+b_{11} & a_{12}+ b_{12} & a_{13}+ b_{13} \\
a_{21} + b_{21} & a_{22}+ b_{22} & a_{23}+ b_{23} \end{array}\right) $$

要するに、行と列の対応する数同士を足し合わせるだけという演算です。

引き算の場合も同様です。

$$ \left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\end{array}\right)- \left(\begin{array}{ccc}
b_{11} & b_{12} & b_{13}\\
b_{21} & b_{22} & b_{23}\end{array}\right) = \left(\begin{array}{ccc}
a_{11}-b_{11} & a_{12}- b_{12} & a_{13}- b_{13} \\
a_{21}- b_{21} & a_{22}- b_{22} & a_{23}- b_{23} \end{array}\right) $$

次に、掛け算に関しては、Ａ×Ｂという行列の掛け算を考える時には「行列Ａの『列の数』」と「行列Ｂの『行の数』」が同じであるという条件がある時のみに演算を考えます。

具体的には次のようにします。
２×３行列と、３×３行列の掛け算です。

$$ \left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\end{array}\right)×\left(\begin{array}{ccc}
b_{11} & b_{12} & b_{13}\\
b_{21} & b_{22} & b_{23} \\ b_{31} & b_{32} & b_{33}\end{array}\right) $$

$$= \left(\begin{array}{ccc}
a_{11}b_{11}+ a_{12} b_{21} + a_{13} b_{31} & a_{11}b_{12}+ a_{12} b_{22} + a_{13} b_{32} & a_{11}b_{13}+ a_{12} b_{23} + a_{13} b_{33} \\
a_{21}b_{11}+ a_{22} b_{21} + a_{23} b_{31} & a_{21}b_{12}+ a_{22} b_{22} + a_{23} b_{32} & a_{21}b_{13}+ a_{22} b_{23} + a_{23} b_{33} \end{array}\right) $$

これは一体どういう計算をやっているのかというと、Ａ×Ｂの「Ａのｎ行目」と「Ｂのｍ列目」について、１つずつ対応する数同士を掛け合わせて加え、「それをｎ行ｍ列目の数とする」という操作です。

a × b 行列と b × c 行列の掛け算の結果は、必ず a × c 行列になります。上記で言うと、２×３行列と、３×３行列の掛け算の結果は２×３行列になります。

この掛け算の定義は一番面倒ですが、行列の計算で一番肝心でもある所です。

行列の掛け算においては、Ａ×ＢとＢ×Ａは一般には違うものになる（同じ場合もあるが同じになる保証はない）事は、行列の重要な性質の１つです。

ｎ×ｎ行列のような正方行列の場合は、足し算・引き算・掛け算のいずれの場合も必ず計算を行えます。

行列は何のために「定義」している？何に使う？

さて、このように行列というものを「定義」すると、それを何のために定義するのか？定義すると、計算をどういう事に使えるのか？という疑問が沸くでしょう。

特に掛け算の定義は面倒で初見だと分かりにくい部分があると思います。しかし、じつはこの掛け算の計算規則が重要で、この形の積と和の組み合わせの式の形を線型結合と言い、主にそれの計算と理論を扱う数学の領域を線型代数と言います。大学数学の中で言うと、行列は線型代数の領域の中で特に重要な位置を占めている・・という位置付けになります。

また、一般の代数学で行列を扱う事もあり（例えば可逆な複素正方行列全体の集合は「群」になるので群論の中で）、その他の分野でも行列を使う事があります。例えば、連立一次方程式を考える時には理論を行列として扱ったほうが便利である事があります。

物理等で行列が直接的に重要になる分野は、例えば量子力学です。これは、先ほど述べた「線型結合」の形によってある種の量が表され、さらに行列の積の形に対応する量も存在する事が大きな理由の１つです。量子化学などの場合は、行列の「群」としての性質を使って物質の構造を調べる手段の１つとして使う場合があります。

掛け算の「九九」というものを日本の小学校では「暗記」させる慣習になってます。

他方、インドでは９の段までだけではなく１１の段、１２の段・・も暗記させるという事が一時期話題になりました。（※）

しかし、これに関しては「９の段まででよい」のです。このページではその理由を一緒に考えてみましょう。

（※） この「インド式」の計算が日本で語られたのは、それゆえに彼らはデジタル分野に強い、などといった文脈においてでした。しかし、個人的には理由づけとしてそれは疑問です。また、インドの全ての人がそのような計算の暗記をしているのかというと、必ずしもそうではないようです。

２ケタの数字同士の掛け算

■ １ケタ×２ケタの数の計算
■ ２ケタの数の掛け算を暗算でやってみる
■ 掛け算の「筆算」の仕組み　

１ケタ×２ケタの数の計算

４×１４といった計算は、電卓を使ってもいいですが暗算でも計算できます。 （「暗記」ではありません。）

答えは５６です。

これは簡単な話で、 ４×（１０＋４）＝４０＋１６＝５６のように計算します。

紙に書いて「筆算」でやってももちろん計算できますが、これくらいだったら暗算でできるという人も意外に多くいるかもしれません。

２ケタの数の掛け算を暗算でやってみる

次に、１１×１２という掛け算を考えてみましょう。答えは、１３２です。

これはどうやって計算するかというと、

• 面倒なので電卓を使う。（あるいはソロバンを使う etc.）
• 「筆算【ひっさん】」を書いて計算する

の、どちらかの場合が多いと思いますが、暗算でやる方法もあります。考え方は上記と同じです。

１１＝１０＋１ですから、１１×１２＝（１０＋１）×１２です。

１０×１２＝１２０で、これはケタが増えるだけなので簡単ですね。（当然、暗記も必要ないです。）

１×１２＝１２でそのままです。

なので、（１０＋１）×１２＝１２０＋１２＝１３２です。

１２＝（１０＋２）と考えても同じようにできます。その場合は１１×１２＝１１×（１０＋２）＝１１０＋２２＝１３２で、もちろん同じ結果となります。

同様に、１４×１５＝１４×（１０＋５）＝１４０＋７０＝２１０などの計算ができます。

１７×１８などになるとちょっと面倒ですが、考え方は同じなのです。
次に述べるように、この考え方は、じつは掛け算の「筆算」の考え方そのものです。

掛け算の「筆算」の仕組み

さて、紙に書く「筆算」というものがありますが、「書く」事自体は数学的な本質ではなくて、１の倍数、１０の倍数、１００の倍数、・・ごとに分けて考える事が本質と言えるでしょう。

例えば、３２４という数は３００＋２０＋４です。

３２４×１２といった計算の「筆算」は、次のような計算をしています。

３２４×１２＝（３００＋２０＋４）×（１０＋２）＝（３０００＋２００＋４０）＋（６００＋４０＋８）＝３２４０＋６４８＝３８８８

掛け算の筆算というものは、この計算で各項の計算結果を忘れないように「紙に書く」のと、ケタが多い時に０を書くのが面倒なので「横にずらす」事でそれを簡略化しているという、それだけの技法です。

筆算の時は基本的に縦方向に書くのも、ケタを揃えて見やすくするというだけの理由でやってるものであり、本質的には横に書いても同じ事です。（小学校のテストで間違わないためには、算数の授業で教わってる通り縦書きで書いたほうがいいとは思います。）

中学・高校数学の「式の展開」とのつながり

■ 「式の展開」と見比べてみよう
■ 日本式かインド式か？

「式の展開」と見比べてみよう

さて、上記のような掛け算の計算自体は小学校でやる内容ですが、本質的には中学以降で教わる「式の展開」（その逆が因数分解）と同じ事と言えます。

式の展開とは、例えば

(x+y)(2a+b)=2ax+2ay+bx+by

と、いった計算です。

３２４×１２＝（３００＋２０＋４）×（１０＋２）という計算と、同じですね。

足し算・引き算・掛け算・割り算の加減乗除の四則演算は数学的にはこのような計算が可能な種類の演算ですよ、という事を「式の展開」は言っているわけです。

式の展開の考え方は、中学や高校でやって終わりというものではなくて、大学の数学や物理等でも普通に使います。しかし別に高度な事をやってるわけではなくて、本質的には小学校の掛け算とやってる事は同じなのです。

日本式かインド式か？

よほど暗記が得意か暗記が大好きで、覚えれるなら１１の段以降も覚えてもよいと思います。（日本の高校生や大学生でも、１１×１１＝１２１、１２×１２＝１４４など、特徴的なものを自然に覚えている人は意外と多いと思います。）

しかし上記の通り、結局９の段まで分かっているなら２ケタの数の掛け算は１の位と１０の位に分けて足し算すればよいわけですから、別に「暗記しなくても計算できる」わけです。しかも、数学的には式の展開の考え方につながる事から、より本質的であるとさえ言えるとも思います。

そういうわけで、１２×１３といった掛け算を「暗記」する必要があるか、子供に暗記させる必要があるかというと「ない」と、個人的には明確に思います。

さらにしかし、ではインドよりも日本の学校の方が勉強の教え方が優れていると言えるか？というと、それは全く別の問題です。個人的には、日本の学校の教え方が特別優れたものと言えるかはかなり疑問です。

なぜかというと、教える教員によっても変わると思うので一概には言えない部分も確かにありますが、日本の学校では「筆算の計算は筆算の計算」「式の展開は式の展開」といった具合に別々のものとして教える傾向が強いからです。しかも、個々の計算問題の正答を書けるかという事が重要視されます。

九九の計算にしてもとにかく強引にでも暗記せよという傾向が強くて論理的とは言い難い教育法ですし、高校や大学の教員でも、計算は「体で覚える」などと平気な顔をして言う人間もいるくらいです。（さすがに、大学の教員であれば今すぐにでも改めるべきだと思います・・。）

どういう仕組みで計算をしているのか理解させる事については、一般的な日本の学校とその教員にとっては大変な「苦手科目」であるのかもしれないのです。

最低でもその事を本質的に改善しない限りは、日本の教育のほうが優れているとは一概に言えないのではないでしょうか。

このページでは分数の割り算について述べます。
内容としては小学校でやる算数ですが、計算の仕方の『理由』について分かりやすく述べます。

分数の割り算の計算方法

■ 分数の割り算：ひっくり返して掛け算しよう
■ ある映画の場面：計算の理由を問いただす少女と、怒りだす姉

分数の割り算：ひっくり返して掛け算しよう

分数の割り算をする時は、分母と分子を入れ替えて掛け算をします。

例えば次のようにします。

$$1 ÷ \frac{1}{3}=1 ×\frac{3}{1}=3$$

$$2 ÷ \frac{2}{3}=2 × \frac{3}{2}=3$$

ある映画の場面：計算の理由を問いただす少女と、怒りだす姉

昔、こんなアニメ映画の場面がありました。

小学生の女の子が、姉から算数の勉強を家で教わるのですが、女の子が「分数の割り算は『なぜ』ひっくり返して掛け算になるのか」と問いただし始めます。

その場面で姉の返答はどういうものであったかというと、机を叩き

「ひっくり返して掛け算するって決まってるのよ！！」

その場面は、それで終わりです。ある女性が子供の頃を回想する場面だったと思いますが、結局『なぜ』に対する答えは語られる事のないまま終わります。

ここでは、『なぜ』に対する答えを考えてみましょう。

理由はじつに簡単なもので、駄々をこねた女の子が悪かったのかというとそうではなくて、おそらく女の子も姉も両方とも、あまり良い形で算数や数学を学校で教えてもらっていなかったと解釈できるかもしれません。

考え方①：「１個の中に半分個はいくつありますか。」

■ １÷１／２ の型の計算
■ １÷２／３の型の計算

\(1÷\frac{1}{2}\) の型の計算

一番簡単だと思われる考え方は次の通りです。

１個の中に、半分個はいくつあるでしょう。もちろん２個ですね。

これが、１÷（１／２）＝２であるという事です。

では、１個の中に３等分した（１／３）個はいくつあるでしょう？もちろん、３個あるのです。
これが １÷（１／３）＝３であるという事です。

もうお分かりかと思いますが、数がいくつでも同じ事であって、例えば１個の中に（１／１００）は１００個あります。

数がもっと大きくても、中途半端な数でも同じです。

$$1÷\frac{1}{721}=1×721=721$$

つまり、次のように計算してよいわけです：

$$1÷\frac{1}{N}=1×N=N$$

また、１『個』でなくとも、１ｋｇでも１メートルでも、何でも同じ事ですね。

２や３を１／２などの分数で割る時は、例えば ２÷（１／２）については１個の中には半分個が２つあり、それが２個あるのですから ２÷（１／２） ＝２×２ ＝４であるわけです。

$$A÷\frac{1}{N}=A×N$$

\(1÷\frac{2}{3}\) の型の計算

では、１を２／３で割る場合はどうでしょうか。

この場合も、計算の工夫をするだけで、考え方は同じなのです。

まず、１を３等分します。すると、１／３は３個あります。これは、前述の１÷（１／３）＝３の計算に該当します。

次に、３の中に、２はいくつあるかというと、３／２です。小数で表すならこれは１.５です。

つまり、

$$1÷\frac{2}{3}=1×3÷2=1×\frac{3}{2}= \frac{3}{2} $$

と、いう事です。

計算の途中で、確かに「ひっくり返して掛け算」になっていますね？

ようするに、１÷（２／３）は、「１／３の２倍」が１の中に何個あるかを調べる計算であり、手順としてはまず分母を掛け算し、次に分子で割ればよいという事なのです。

整理すると、次のような形です。

1. 分母の数で等分する事で、小さいパーツを分母の数だけ作る、→　つまり分母倍する
2. 分母の数で等分したパーツにそろえているので、それを分子の数で割ればそのまま答えになる。　→　分子で割る
3. 結果的に、計算は「分母を掛けて」「分子で割る」事で行える　→　つまり、分母と分子をひっくり返して掛け算すればよい。

割る対象が１ではなくて２や３や他の数でも同じ事で、従って次のように言えるわけです：

$$A÷\frac{M}{N}=A×N÷M= A×\frac{N}{M}$$

割られる数のほうの A も分数や少数であっても構いません。考え方は同じ事です。

考え方②：掛け算と割り算は「逆演算」の関係にある

■ 掛け算と割り算は互いに逆演算の関係
■ 中学・高校的な考え方　

掛け算と割り算は互いに逆演算の関係

別の考え方もあります。こちらのほうが、より「数学」でよくやる考え方です。

分数とは、そもそも割り算であるという事にまず注目します。つまり、例えば１／３を掛けるという事は、３で割る事に他ならないわけです。

分数２／３などを掛ける場合は、３で割って２倍する（２を掛ける）と解釈できます。つまり次のように書けるわけです。

$$1×\frac{2}{3}=1÷３×2$$

ここで、掛け算と割り算は、計算の順番を入れ替えても結果は同じという事は重要です。たとえば、１２を２で割って３倍すると１８ですが、順番を入れ替えて１２を３倍してから２で割っても同じ１８になるのです。

$$1×\frac{2}{3}=1÷３×2=1×2÷3$$

さて、分数の割り算ではなくて普通の割り算の時に、？÷３＝２という問題で「？」の部分を出すには、３で割って２になる数を見つけるわけです。それは６ですが、これは２を３倍してあげる事で見つける事ができるのです。つまりこのような問題では、割り算の部分を掛け算にする事で「？」の部分の答えが見つかります。

また、今度は掛け算の２×？＝６という問題で「？」の部分を見つけるには６を２で割って３であると計算できます。「２を掛けると６になる数を見つける」事と、「６を２で割る」事は計算としては同じ事であるわけです。

次に、分数の割り算 「１を２／３で割る」を考えましょう。 この答えを仮にＰとおきましょう。

$$ 1÷\frac{2}{3}=1 ÷（ 2÷3）=P$$

すると、 ？÷３＝２ という問題で「逆算」して掛け算で「？」の部分を見つけたのと同じ要領で

$$1=P×\frac {2}{3} =P×(2÷3)= P×2÷3 $$

となるのです。これをよく見てみると、1 = P × 2 ÷ 3 という関係になっています。という事は、「？÷３＝２」や「 ２×？＝６」の問題と同じ形です。もう一度逆算してあげると、P の値を表せます。

1. 1 ＝ P × 2 ÷ 3
2. 1 × 3 ＝ P × 2
3. 1 × 3 ÷ 2 ＝ P

つまり、

$$P=1 × 3 ÷ 2 =1×\frac{3}{2}$$

であるという事ですが、もともとは

$$P＝１÷\frac{2}{3}$$

だったのですから、

$$1÷\frac{2}{3}= 1×\frac{3}{2} $$

という事です。

掛け算と割り算が逆の演算である関係からは、必然的に「分数による割り算」は「分子と分母を入れ替えた掛け算」になる事を意味しています。

中学・高校的な考え方

やる事は本質的に上記と同じですが、等号で結んだ関係を同じ数で掛けたり割ったりしても等号関係は保たれる事を利用する方法もあります。

$$１÷\frac{2}{3} =P$$

式の左と右の両方の側（両辺）に「２／３」を掛けます。この時、式の左側（左辺）では、 「２／３」 で割って 「２／３」 で割るのですから、その部分は何もしない（１を掛ける）のと同じ事になります。

$$１÷\frac{2}{3}× \frac{2}{3} =P × \frac{2}{3} $$

$$ 1=P × \frac{2}{3} $$

この両辺に、今度は「３／２」を掛けます。

$$ 1×\frac{3}{2}=P × \frac{2}{3} ×\frac{3}{2} =P$$

つまり結果は同じで、分数の割り算は分母分子を入れ替えた掛け算になります。

$$ １÷\frac{2}{3} = 1×\frac{3}{2} $$

この両辺にさらに、同じ分数を掛け算する形の計算により、一般に次のように言えます。

$$\frac{A}{B}÷\frac{M}{N}= \frac{A}{B} × \frac{N}{M}=\frac{A × N}{B × M} $$

まとめ

逆演算という考え方は、数学的には非常に広い範囲で使われるので考え方としては知っておくと便利です。より一般的には、２を掛けて２で割るといったように、ある演算と逆演算の「積」は１（恒等）、つまり何もしないのと同じになるという考え方をして話を進める事があります。

しかし、単純に普通の分数の計算で「割り算はなぜひっくり返して掛け算なのか」という素朴な疑問に対する答えは前述の「１個の中に半分個は２個ある」の考え方でも良いと思います。どちらにせよ、計算結果は同じになるからです。

もう１つ、そもそもそのように計算を『定義』してしまって、その定義のもとで話を進めているのだとする考え方もあります。特に数学者という人達は具体的な『モノ』を使って説明する事を嫌う傾向にあるので、「なぜですか」と聞かれたら「定義だ」と答える事が多いでしょう。

数学という学問の中での考え方としてはそれは間違っていないのですが、『説明』としては女の子の質問に対して怒りだして暗記を強要する姉とほぼ同じである事には注意が必要かとは思います。

確かに基本的には、計算の結果が合っていれば「説明できる」必要は必ずしもないのです。計算というのは、要するに答えが合っていればよいという考え方もあるからです。しかし、子供が何か疑問に感じた場合にはきちんとそれに答えるという事も算数・数学教育では大事な事だと思います。特に、生徒からの質問に対しては、大人は誠実な気持ちで適切に対応する必要があるでしょう。