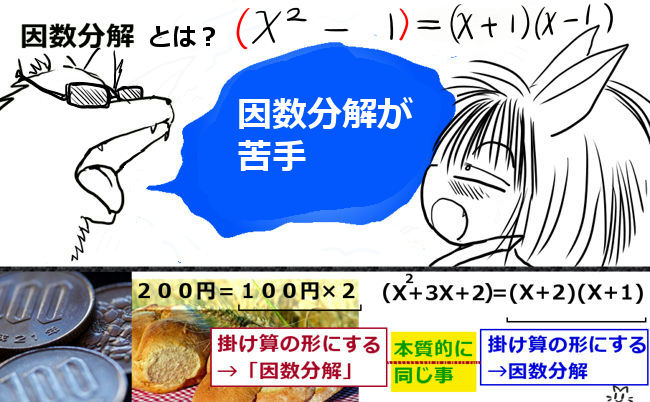
三角形の相似条件は高校入試を始めとして中学数学では重要事項の1つです。
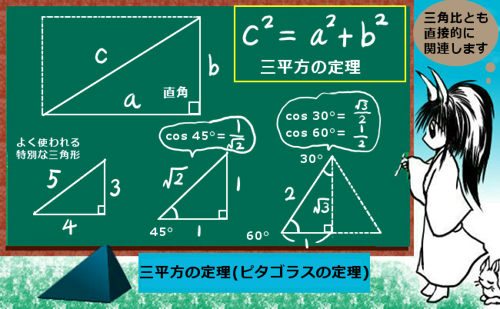
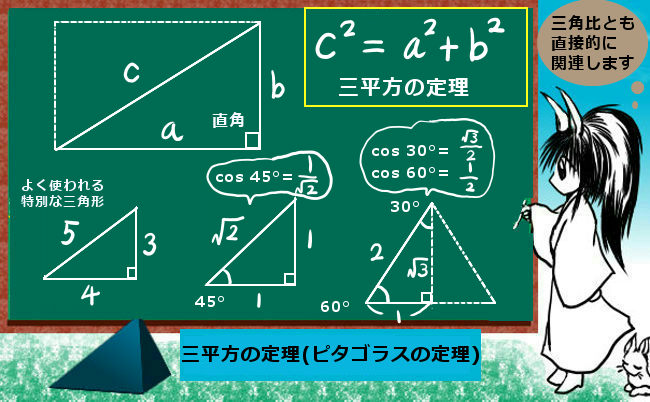
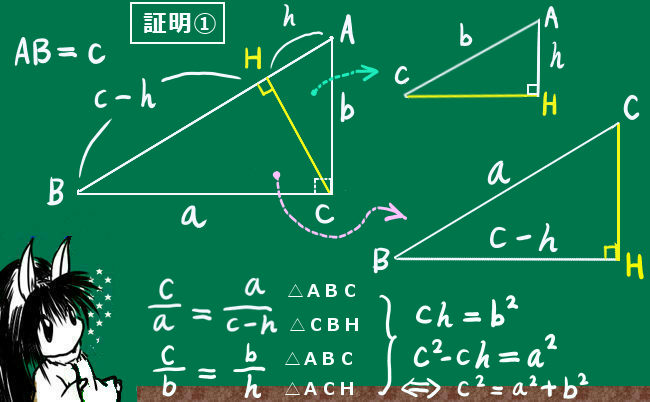
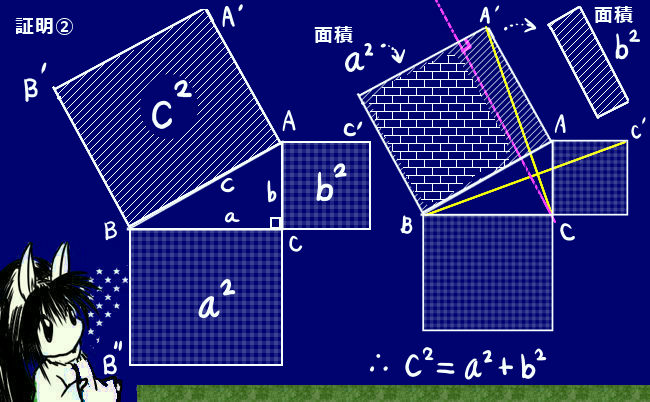
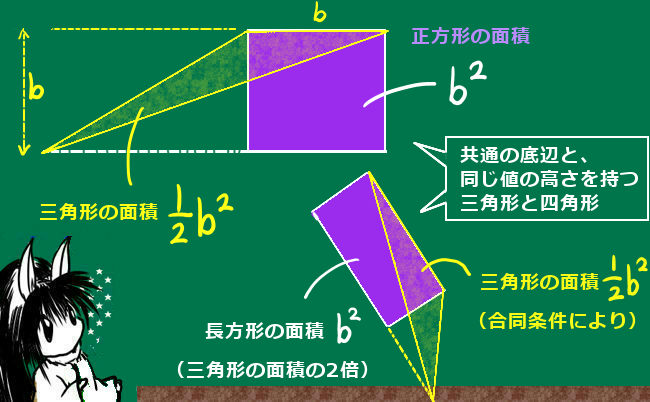
図形問題を解くために必要という事でもありますが、三平方の定理などの重要な定理が成立するための根拠の1つになっている事なども重要と言えるでしょう。
平面において2つの三角形が「相似【そうじ】」であるとは、
ごく簡単に言うと「大きさは違うが形は同じ」であるという事です。
★これに対して、「大きさも形も同じ」なのが三角形の合同です。
意味する事と、成立する条件の違いに注意しましょう。
合同と相似は一見似ていますが扱い方が違うものなので、気を付けましょう。
「2つの三角形が互いに合同」ならば「2つの三角形は互いに相似でもある」と、確かに言えます。
しかしこの逆は成り立ちません。「相似であるから合同でもある」と言ったら、それは間違いです。
【※中学数学の範囲外になりますが詳しくは必要条件と十分条件の関係から把握する事になります。合同である事は相似である事を含んでいるという包含関係になります。】
そのため、合同と相似をごっちゃにしてはならず、関係を意識しながらも丁寧に別々に整理する事が必要であり、重要でもあるのです。
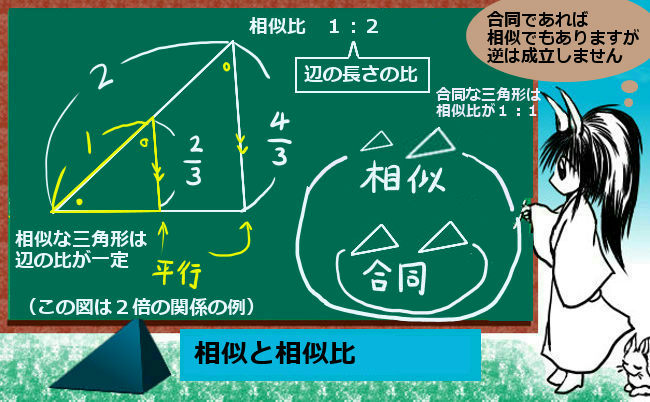
もっとも、単に見た目が似ているというだけでは相似であるとは言わず、きちんと数学的な条件があります。
相似条件と証明での使い方
次の3つの条件の「いずれか」を満たす2つの三角形は互いに相似であると言います。「いずれか」という事は、「1つでも当てはまればよい」という事です。
次のいずれか1つが成立するならば2つの三角形は互いに相似です。
- 2組の角の大きさがそれぞれ等しい
- 2組の辺の長さの比と、その挟む角の大きさがそれぞれ等しい
- 3組の辺の長さの比がそれぞれ等しい
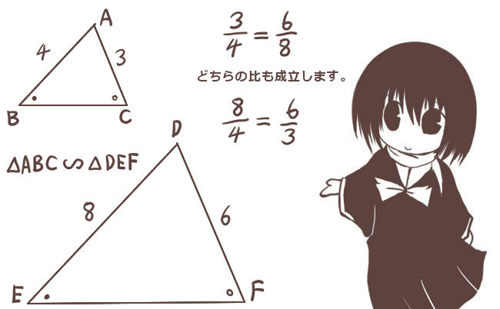
この時「△ABCと△DEFは(互いに)相似である」などと言い、△ABC∽△DEFとも書きます。(無限大の記号に似てますが別物です。)この時、「同じ形」として対応する角が順番通りになるように書きます。
相似な2つの三角形の互いの「辺の長さの比」を相似比と言います。例えば1:2とか1:3という関係が成立します。場合によっては整数比とは限らず、1:\(\sqrt{2}\) とか2:\(\sqrt{3}\) などの相似比もあり得ます。
三角形同士が相似である事がひとたび判明すれば、これら3つの条件は全て成立します。つまり、例えば2組の角度が等しいという条件が成立すれば、3組の辺の長さの比もそれぞれ等しいという事です。
ただし、相似である事を証明するためにはどれか1つだけ判明していればよいという事です。
★比較する2つの三角形が直角三角形であれば、その時点で「対応する1つの角がそれぞれ等しい(90°で等しい)」事は言えているので、もう1つだけ等しい角度を見つければよいといった作業になります。
繰り返しますが合同条件と似ていますが違うもの(相似条件のほうが制約が緩い)なので注意しましょう。
例えば、辺の長さが分からないけれど角度だけで比較できるのは相似条件のほうであって、合同条件にはそのような条件はないのです。(暗記するのではなく意味を考えてみると分かりやすいと思います。角度だけが分かっている場合、形は同じであっても辺の長さは伸び縮み可能なのです。)
合同である場合は「相似比」が1:1であると言う事もできます。それが「大きさも同じ」という意味であって、大きさが異なる場合には相似比が1:2とか2:3とかになるわけでそのような場合も含めた「形は同じだが大きさは異なる」関係を相似と呼ぶわけです。
2つの三角形が相似である事を正確に見るには、「証明」が必要です。これは、見た感じ「同じ形」に見えるけれど実際は違う(辺の比が一定にならない、角度が異なる)という事があるからです。
高校入試の出題として多いのは「2組の角の大きさがそれぞれ等しい」事を使うパターンです。これは、同じ大きさの角度である部分が2つ見つかればよいという事です。
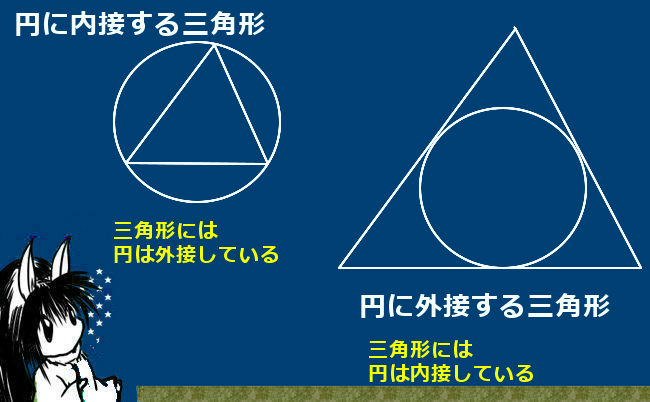
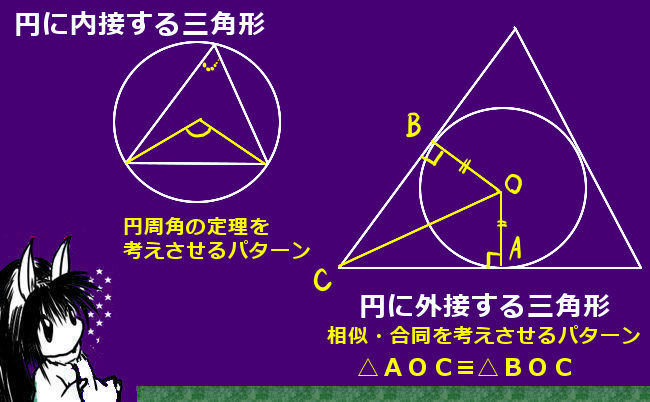
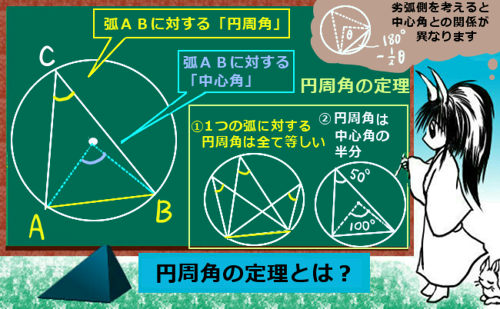
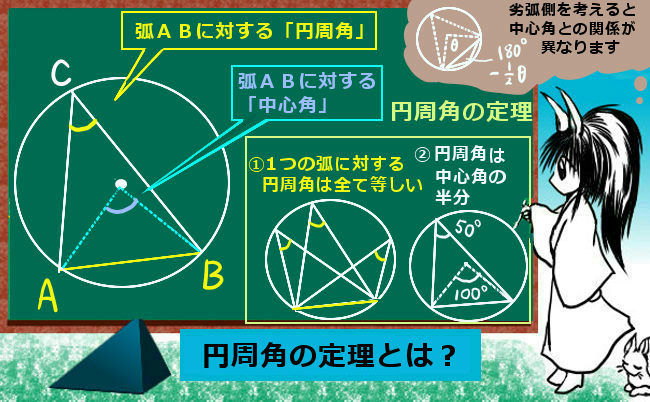
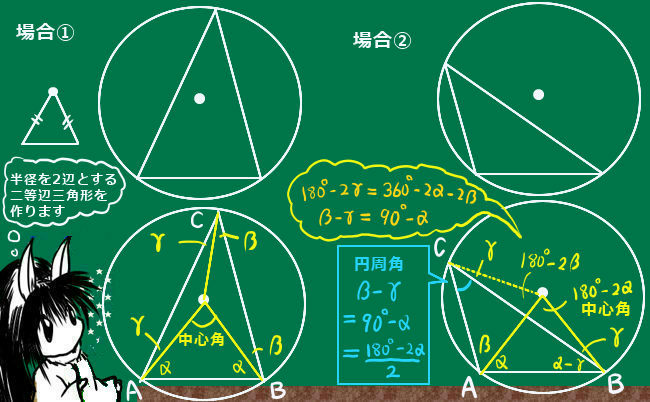
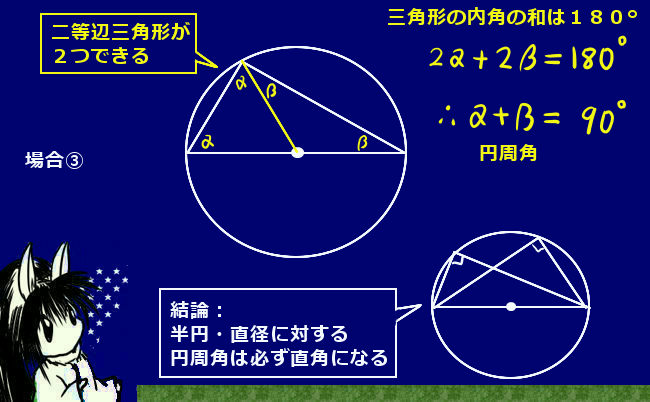
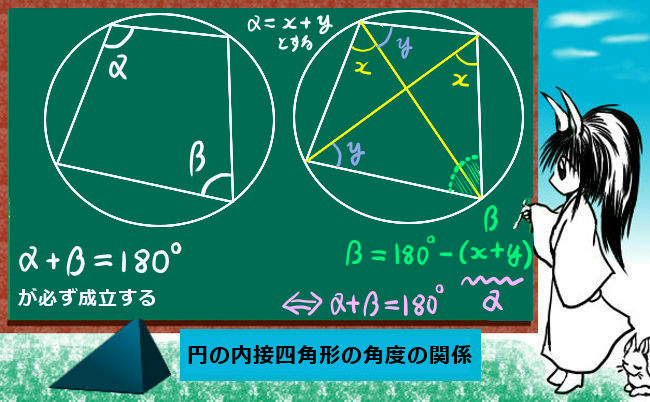
より具体的には、対頂角の関係、平行線の同位角・錯角の関係、円周角の定理などを使って「角度の大きさが等しい」事を示します。また、共有する角がある場合にはもちろんその角度は2つの三角形で等しいのです。
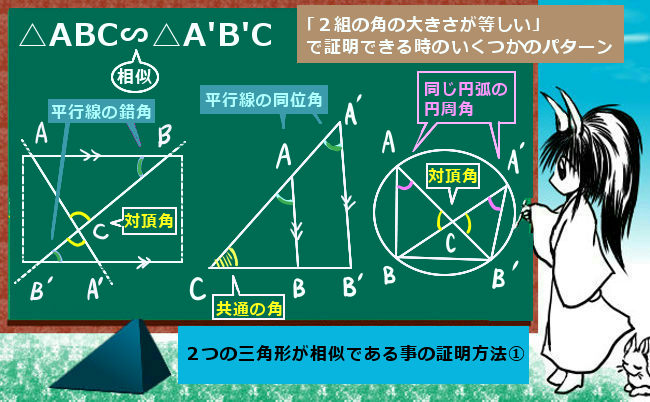
残りの2条件は証明の時に使う事もありますが、むしろ相似である事が証明された後に辺の比や面積比を計算させる問いで使われる事が多いように思います。
相似な三角形の面積比
三角形の相似比(辺の長さの比)が1:nの場合、面積比は1:n2になります。
これは、例えば1つの三角についての底辺がn倍、高さについてもn倍になるためです。
高校入試ではよく問われる事項です。
辺の長さの比が1:nの相似な三角形の面積比は1:n2になります。
(辺の長さの比がa:bなら、面積比はa2:b2)
例えば底辺が2、高さが3の三角形の面積は2×3÷2=3ですが、
各辺の長さが2倍になったとすると、高さも2倍になる事に注意して
面積は(2×2)×(3×2)÷2=12
つまり2×2=4倍になるという事です。
これは公式として関係式を暗記するのではなく、図に描いてイメージしながら練習してみたほうがよいと思います。
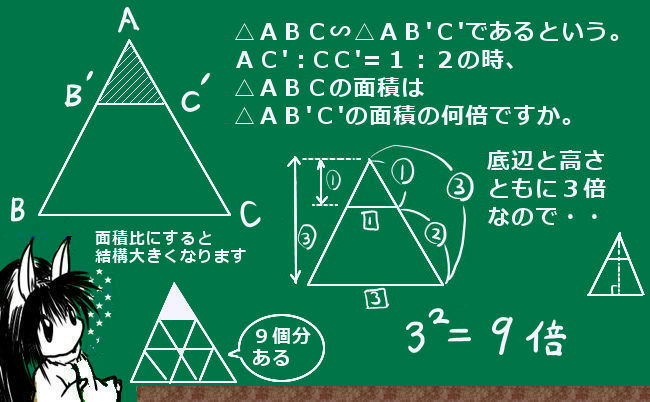
辺の長さの比が1:3ではなく2:3のような場合は面積比は22:32=4:9です。
$$辺の長さの比が2:3であれば大きい三角形の面積は小さい三角形の\left(\frac{3}{2}\right)^2=\frac{9}{4}倍$$
辺の比に関する補足説明
相似な三角形の辺の比に関して、補足的な説明をします。
三角形同士が相似である場合に「対応する辺同士の比」は等しくこれを相似比と言うのは前述の通りです。
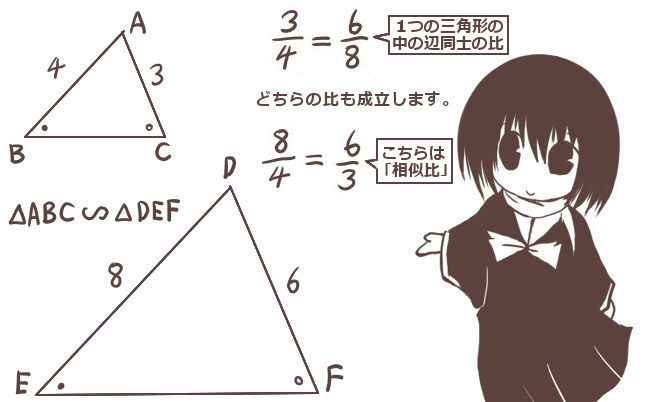
他方で「同じ三角形の中の辺同士の比」も、相似な2つの三角形で等しくなるのです。これは1つの三角形の中で3通りの比がありますからもちろん一定ではなく、一般的に相似比とも異なる値になります。
しかし、例えば△ABCでAB:BC=1:3であったとすると、それに相似な三角形△DEFがあったときにDE:EF=1:3という事も同じく言えるという意味です。
この時、AC:AB=2:5であれば同様にDF:DE=2:5という事です。
(※この場合、この条件だけから具体的な相似比は分からない事には注意。互いの対応する辺の長さの比に関して、相似比という一定の比がある事だけ分かります。)
式で書くと、△ABC∽△DEFであれば、
AB/DE=AC/DFという比の関係(この一定の比が相似比)に加えて
AB/AC=DE/DF という関係も成り立つという事です。
これは、じつは結構単純な話です。
AB/DE=AC/DF の両辺をACで割り、両辺にDEをかける事で得られます。
式変形をしなくても相似関係にあるという事は同じ形で大きさだけが異なると意味を考えれば分かりやすいかと思います。
辺の長さの関係を丁寧に整理する必要がある場合もある事にだけ注意。
証明問題も含めて、図形問題が得意になるコツはあまり難しく考えない事です。
意味を考えながら図を描いてみましょう。
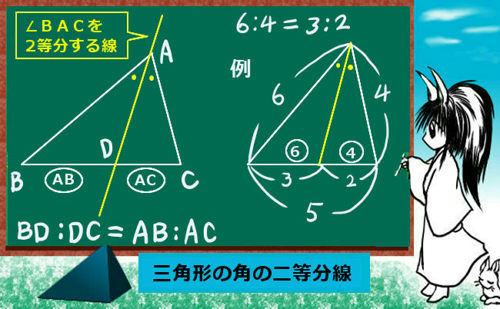
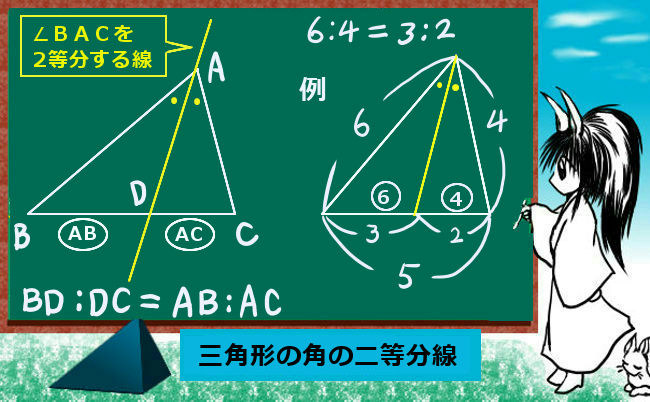
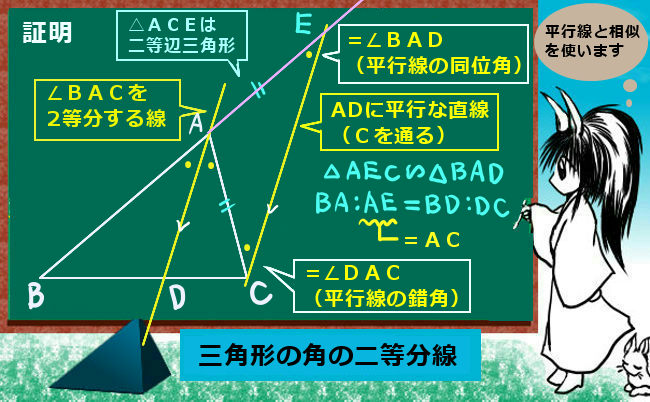
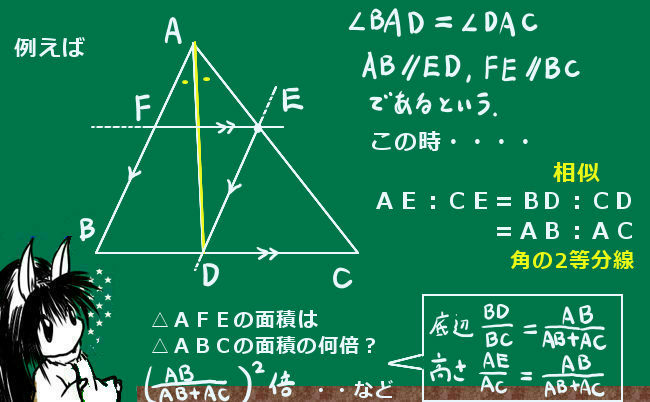
他に図形問題として関連が深いのは角の二等分線と三角形の辺の比の関係などで、これは三角形の相似を根拠として成立します。三角形の相似についてじゅうぶん理解していれば、関係式を暗記せずにその場で導出する事も可能なのです。
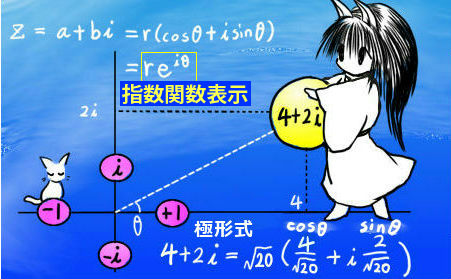
「形」さえ同じであれば、三角形の中の2辺の「比」が一定であるという事は、三角比の考え方の基礎となっています。これは、直角三角形に限定して、特定の角度に対しては2つの辺の長さは一定になる事を利用して決められるものです。高校数学で教えられるものですが、考え方としては三角形の相似の考え方が分かっていれば理解できる内容になります。