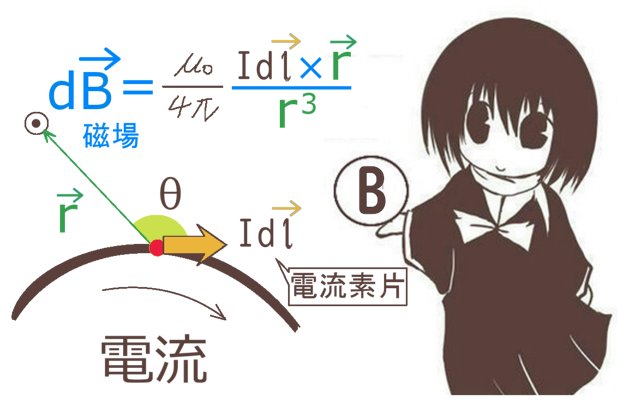
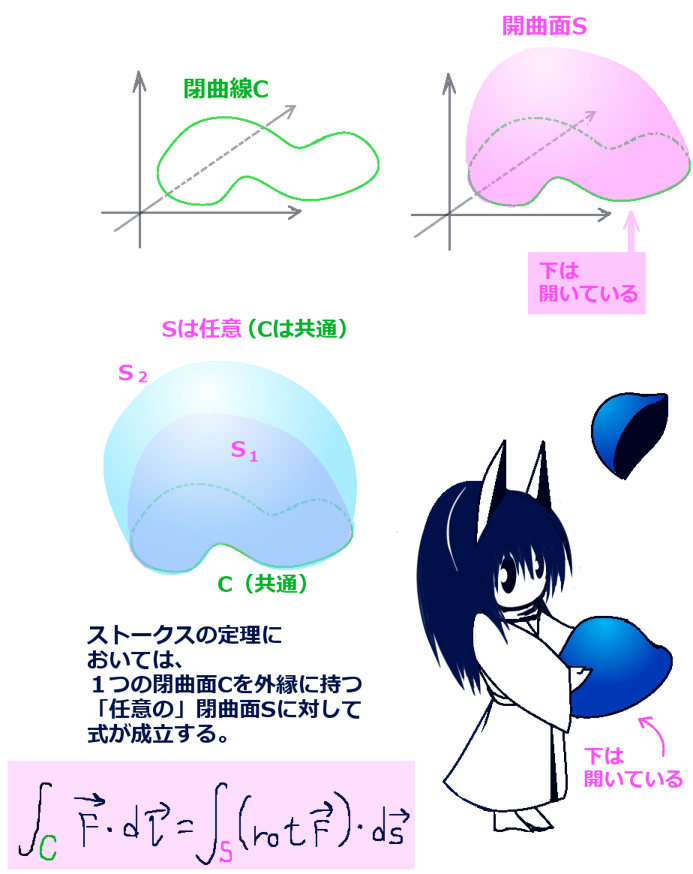
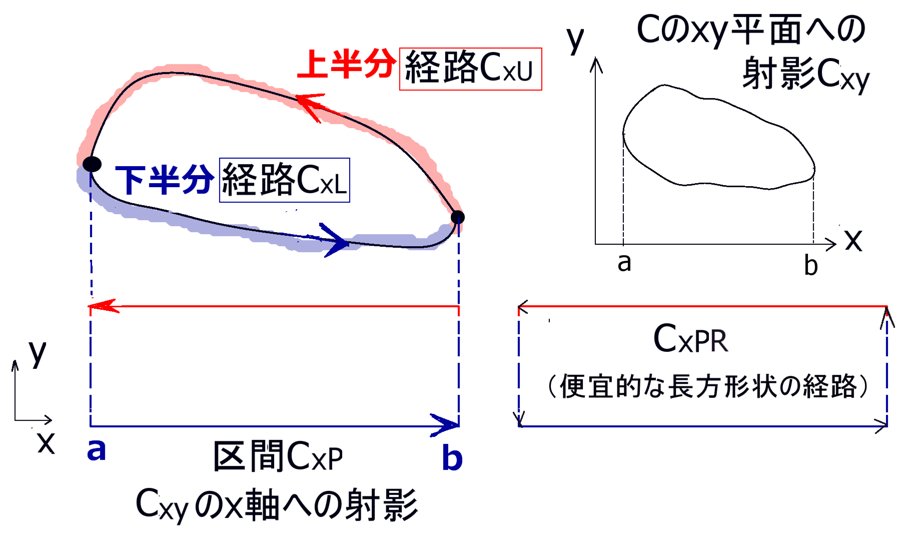
立体角(solid angle)は、平面上の角度を空間的な広がりに拡張したものであり、球の表面積を利用して表されます。通常の平面の角度の事は、この記事では主に「平面角」と表記します。
立体角の単位は無単位とする事もありますが【sr】(steradian) という単位も一応あります。この記事では平面角のラジアン【rad】と区別する目的で、立体角に対して単位を付けて表記している事があります。
平面角はθで表される事が多いのに対して立体角はΩあるいはω(いずれも「オメガ」)で表記される事が多く、この記事でもその文字を使用します。Ωという文字は、電気抵抗の単位でも使われてその時は「オーム」と読みますが、ここではその意味ではなく文字の1つである「オメガ」として使用します。
立体角の定義と「錐面」
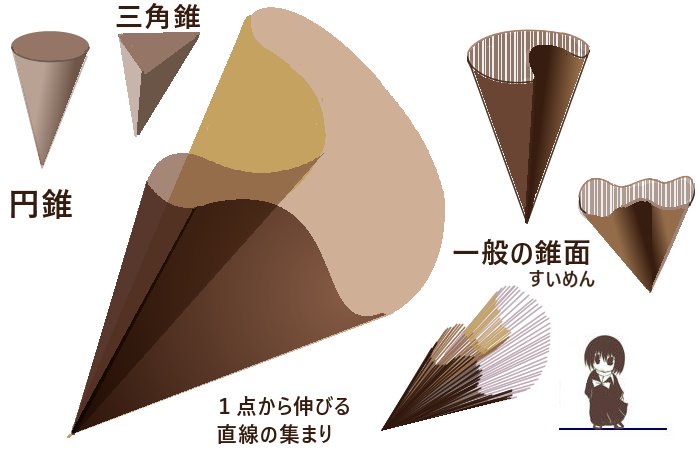
あまり聞き慣れない語かもしれませんが立体角の定義には錐面(「すいめん」)という言葉を使うと表現的に便利です。(使わなくても定義はできますがここでは使用する事にします。)
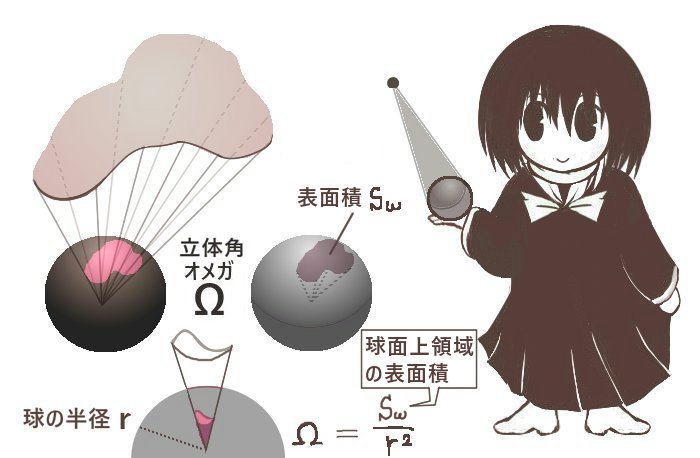
立体角は1つの点を基準として球面(範囲は任意)に対して錐面が囲む領域の表面積でとして定義されます。「錐面」とは円錐や三角錐などをより一般的に表した立体的な図形の側面の部分を表します。
錐面とは空間内の「1点」から伸びて1つの閉曲線を通過する直線の集まりによって形成される曲面を指します。(三角錐の側面のように平面状である物も含みます。)
1点を通過する直線の集まりとしても考えられますが、立体角を考える」場合には普通は半直線の集まりとしての錐面を考えます。
錐面を形成する閉曲線が円であればそれが「底面」を成して全体を構成する立体(錐体)
は円錐であり、三角形であれば三角錐、四角形であれば四角錐となるといった具合になります。
立体角を考える時には模式的に円錐状の広がりを考える事も多いですが(分かりやすいので)、考える錐面は理論上は色々なものがあってよい事になります。
立体角Ω【sr】はある1点Oからの3次元空間的な広がりを定量的に表します。
Oを中心とする半径rの球面において
「Oを頂点とした錐面で囲まれる領域」の面積をSωとした時に、次式で表されます。
$$\Omega=\frac{S_{\omega}}{r^2}$$
ところで球の表面積は \(4\pi r^2\) で表されるので、実はこの式は
考えている球の半径の具体的な値に関わらず立体角は同じ値になる定義となっています。
そこで、錐面で囲まれる球面上の領域の面積を「球面全体の面積のK倍」とすると次式で考える事もできます。
$$S_{\omega}=4\pi r^2Kと置く時、$$
$$\Omega=\frac{S_{\omega}}{r^2}=4\pi K$$
つまり立体角は4πの倍数(任意の実数倍ですが普通は1以下の有理数)で表され、
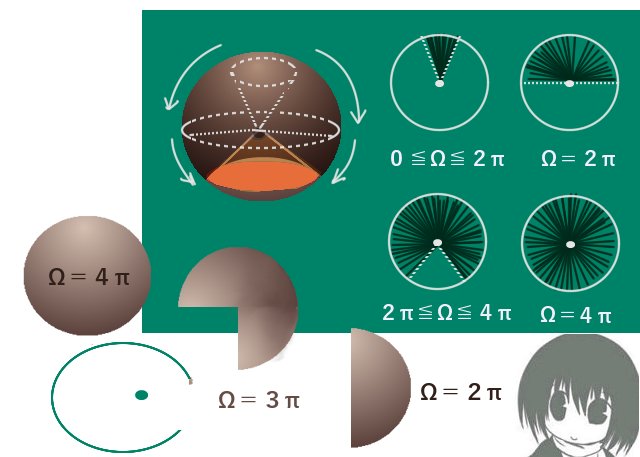
半球全体の広がり(空間全体の2分割)を表す立体角は2π【sr】です。(K=1/2)
次に見て行くように立体角は考えている球面(あるいは任意の曲面)がプラスとマイナスの符号の違いがあり、さらに任意の実数の値を考える事ができます。
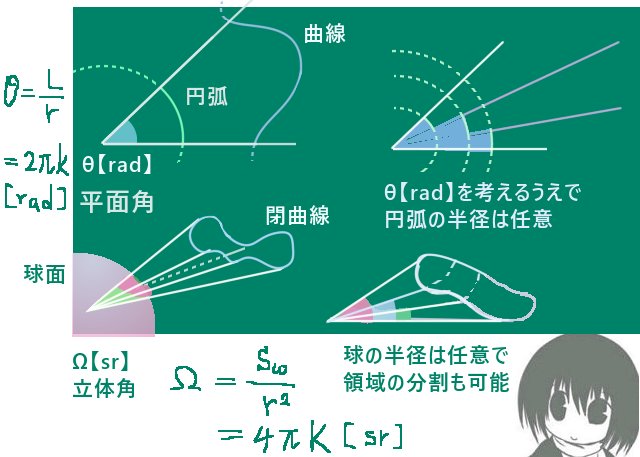
平面で通常の角度である平面角θを考える時も実は同じような考え方がなされています。
原点から伸びる2直線と、原点を中心とするてきとうな半径rの円との交点を考えて、その円弧の長さLを半径rで割った値が弧度法での角度θであると言えます。つまりθ=L/r【rad】と考えていて、L=2πrkとおくならθ=2πk【rad】であり、すなわち
「2πの何倍か」によって平面上の1点から伸びる2直線の広がりを角度θで表している
というわけです。
ただし平面角の場合、その倍率であるkは任意の実数値ですが普通は敢えて無理数では考えずに有理数を使う事が多いわけです。
90°であれば2π/4=π/2【rad】
60°であれば2π/6=π/3【rad】
45°であれば2π/8=π/4【rad】のようにしている事の
拡張が立体角の考え方であると言えます。
ただし立体角の場合は、同じ立体角の値となる広がりの錐面の形状は一般的に1つとは限らず様々な形状があり得ます。
立体角の大きさの範囲
立体角を0【sr】から2π【sr】に増加させると、広がりとしては半球の大きさ分になります。
図形的に見るとそこから先も半球分に立体角を加えていく事は可能に見えるわけで、実際そこからさらに立体角を増やす事は可能です。
立体角が2π【sr】を超える時には図形的には錐面は球面の反対側の領域を切りとっていく事になるはずです。この時に錐面と球面の交わりで作られる閉曲線の「内側」と「外側」の関係を統一的に考えて、0【sr】から始めて「閉曲線の内側」と考えていた向きを2π【sr】から先も保つとします。
すると、錐面が切り取る球面上の領域の表面積は2π【sr】にさらに値が追加されていく事になります。それを続けると立体角は「球の内側から見た球面全体に対する広がり」(すなわち「空間全体」に対する広がりと同じ)を表す4π【sr】まで増加します。
つまり通常の3次元空間での立体的な広がりを表すには、立体角の「大きさ」は0≦Ω≦4πの範囲で考えれば十分という事になります。球全体の表面積に対する倍率では0≦K≦1を考えています。
ただし後述するように、曲面に対する表裏の関係で立体角を符号も含めて考える時は
マイナスの値も含まれるようになって範囲が-4π≦Ω≦4πとなります。(さらにその範囲外の場合も立体角は定義されますが、ここでは原則として除いて考える事にします。)
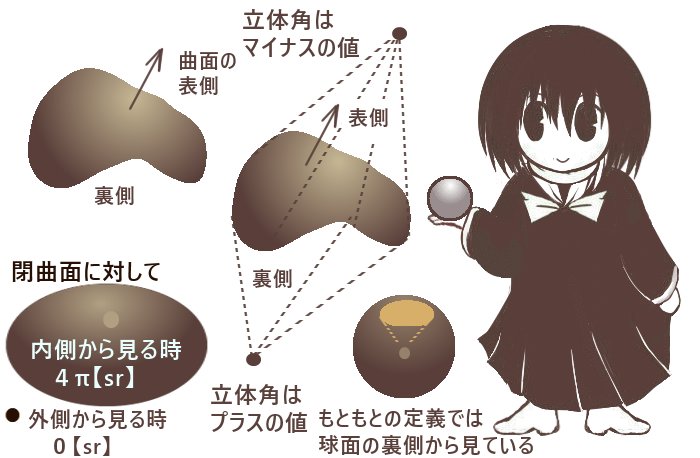
後述するように、あるいは図形的に考えて閉曲面内に立体角を考える点を設置して閉曲面全域に対して立体角を考える場合にはその立体角のは符号も含めて4π【sr】です。逆に閉曲面の外側から閉曲面全域についての立体角を考えると、その立体角は0【sr】になります。(閉曲面の外側から閉曲面全域の立体角を考える場合、閉曲面を2に分割して同じ大きさのプラスマイナスの符号だけ異なる立体角を合計する事で0になります。)
動く点から1つの曲面に対して立体角を考える場合には
点が曲面の外を通って1周した後に曲面を通過してもとの位置に戻る時に、
曲面通過時に立体角が4π【sr】または-4π【sr】変化するという事が起こります。
ただし通常の図形的な考察ではその場合を考えなくてもよいので、
以下ではその場合を除いて考えていきます。
立体角が負の数である時の定義
立体角Ωが0≦Ω≦4πの範囲の時、
立体角を考える基準の点は球面(半径に関わらず)の内側にあります。
そこで、空間内のてきとうな位置から何かの曲面に対して立体角を考える時には
曲面に表と裏がある時には次のように立体角の符号を決める定義をします。
- 基準点が曲面の裏側にある時:立体角の値の符号はプラス+
- 基準点が曲面の表側にある時:立体角の値の符号はマイナス-
ここでの曲面の表裏の関係は、法線面積分等を考える時の意味での曲面の表裏と同じです。
符号の関係をここでの場合とは逆にしても定義は可能ですが、ここでは混乱を避けるためにこの定義のもとで話を進めます。
ここでの「表側」「裏側」という事をより具体的に言えば、
曲面の外縁となっている閉曲線の各点から基準点に向けての錐面を構成する線分が曲面の表面側から出る方向を向いているか、裏面側から出る方向を向いてるかの違いになります。
法線面積分およびガウスの積分との関係式
立体角は前述の符号も含めた関係の定義のもとで、
てきとうな曲面Sがあった時にその曲面上の法線面積分で表す事ができます。
さらに立体角を法線面積分で表す時、被積分関数はガウスの積分【位置ベクトル(x,y,z)を距離の3乗で割ったものに対する「閉曲面」上の法線面積分】での被積分関数になります。
そのため、特にSが閉曲面の時には立体角は-4π≦Ω≦4πの範囲においてガウスの積分として値が3通りに決まります。
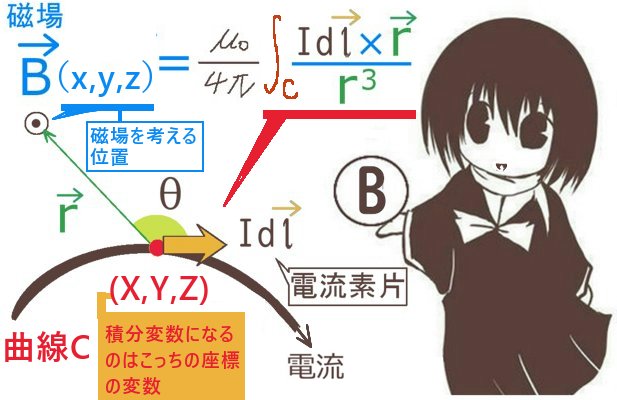
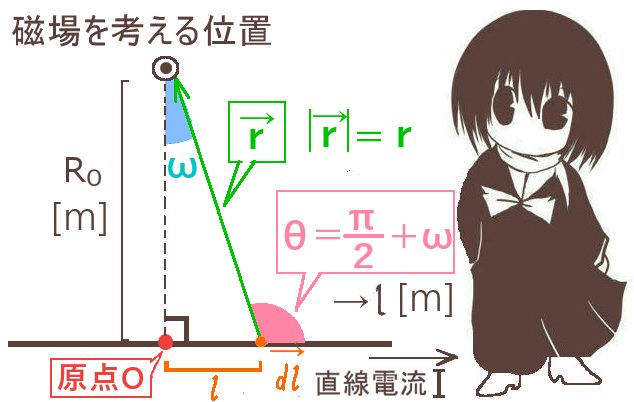
原点をOとして\(\overrightarrow{r}=(x,y,z)\) として、その大きさはrで書きます。
ある曲面Sの外縁となっている閉曲線の各点から原点に直線を引いて錐面を作った時、
原点Oから見た立体角は次のように符号も含めて法線面積分で表されます。
$$\Omega=\int_S\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}$$
■右辺を勾配で表した時
$$\Omega=-\int_S\left\{\mathrm{grad}\left(\frac{1}{r}\right)\right\}\cdot d\overrightarrow{s}$$
■特に曲面Sが閉曲面である時
上記の積分はガウスの積分であり、
値は原点OとSの位置関係によって次の値になります。
| 原点Oの位置 | 立体角Ωの値(およびガウスの積分の値) |
| 閉曲面Sの内部 | \(\Omega =4\pi\) |
| 閉曲面Sの外部 | \(\Omega =0\) |
| 閉曲面S上 | \(\Omega =2\pi\) |
閉曲面を考える場合には閉曲面に対して立体角を考える点が
「内部にあれば裏側」「外部にあれば表側」という事が確定するので、
-4π≦Ω≦4πの範囲で立体角が符号も含めてこれらの3通りに決まります。
ある点から曲面あるいは閉曲線に向けての立体角を考える時、その立体角を曲面等から点に向けて「張る」立体角であると表現される事もあります。
立体角を法線面積分で表す関係式を導出する方法としては、
曲面を細かい平面に分割して角度(平面角)の関係から微小面積に対する関係式を考えるか、もしくは最初から積分で考えてみてガウスの発散定理を適用する方法があります。
曲面が閉曲面の時にはガウスの積分そのままの計算であり、値の導出の計算にはガウスの発散定理を使うと導出する事ができます。
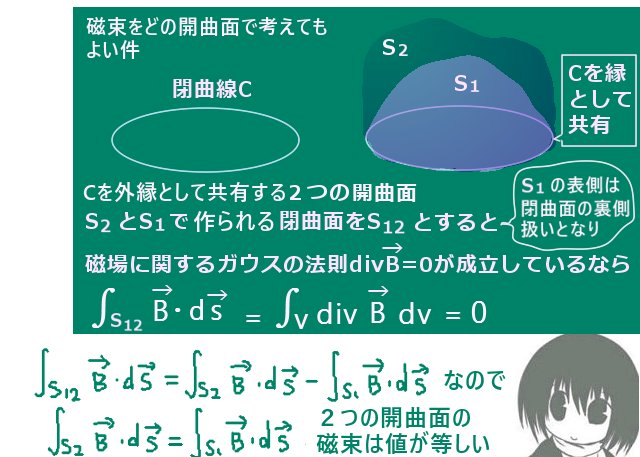
立体角の定義から考えると、外縁となる閉曲線を共有する複数の開曲面に対して錐面の延長をはみ出さない限りは「立体角は1つだけの値として決まるはず」です。
その事は、立体角を考える点から見て「曲面の表裏の関係が同じであれば」成立します。
【積分の表記の場合でもガウスの発散定理を使う事でそれが成立する事を確認できます。下記の2番目の方法でも触れるように、\(\overrightarrow{r}\)/(r3)の発散は0である事を使用します。】
この場合、錐面から曲面がはみでている場合でもはみ出た部分によって閉曲面を考えると、その部分の符号も含めた立体角はガウスの積分で表せることから0となって消えるので立体角の大きさに影響しない事になります。
他方で、立体角を考えている点Oに向けて閉曲線から曲面を引っ張ってきたような場合には話が変わってきます。例えばそれで1つの曲面が点Oに重なる場合には積分の表記で考えると実は2つの曲面に対する立体角には2πの差ができます。さらに、閉曲線を共有する1つの曲面ともう1つの曲面が1つの閉曲面として点Oを内部に含むようになると、2つの曲面に対する立体角には4πの差が生じます。【その時に2つの立体角についてΩ1=Ω2+4πという関係になります。立体角は4πを超える事もありますが、ここでの場合に限定して言うと片方の曲面の表裏の関係を保ったまま動かしているのでΩ2はマイナスの値の立体角となり、Ω1<4πとなります。】
微小面積で考える場合の導出
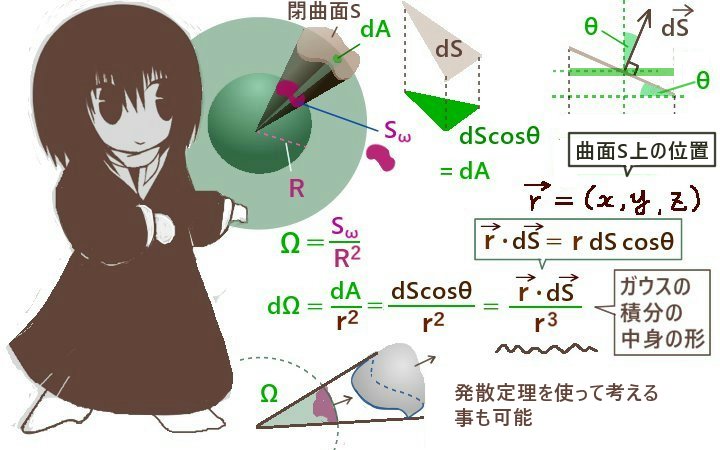
立体角を考える基準点の原点Оは開曲面Sの裏側のほうに位置しているとします。
まず球面の領域の表面積から立体角を考える定義のもとで1つの立体角は球面の領域を分割して考える事ができて、さらに考える球面の半径は任意でよい事から分割した微小領域ごとに立体角を考えるための球の半径を自由に設定できます。
ここで球面を微小な平面領域で近似する場合には一般的に半径が大きい球のほうが細かい分割が必要なので、大きい半径を考える時ほどさらに細かく分割を行うものとします。
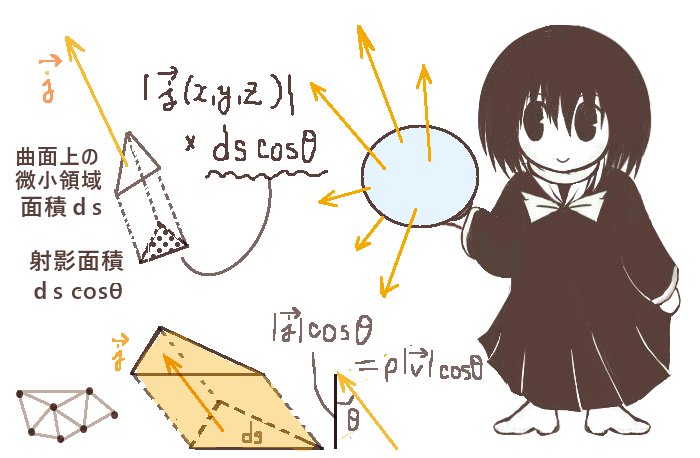
分割は球面上および曲面上の3点をつないで三角形領域で行うとして、
曲面Sの分割領域の頂点から原点Оに向けて直線を引き、球面に対しても微小領域の頂点がその直線上にあるように分割を行います。必要に応じて分割はより細かくします。
\(\overrightarrow{r}=(x,y,z)\)を考えて、球面の微小領域がその点を含むように位置で球の半径を調整します。(積分をする時にはS上の微小領域上にベクトルを平行移動させるとして考えます。)
\(\overrightarrow{r}\)は原点から(x,y,z)に向かうベクトルであり、原点を中心とする球の球面に対して垂直です。
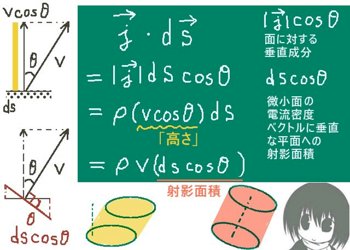
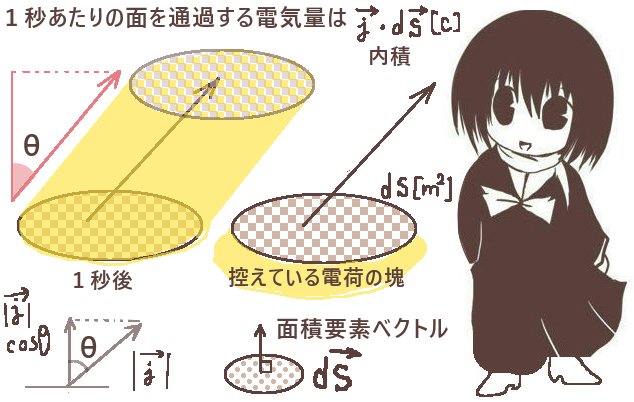
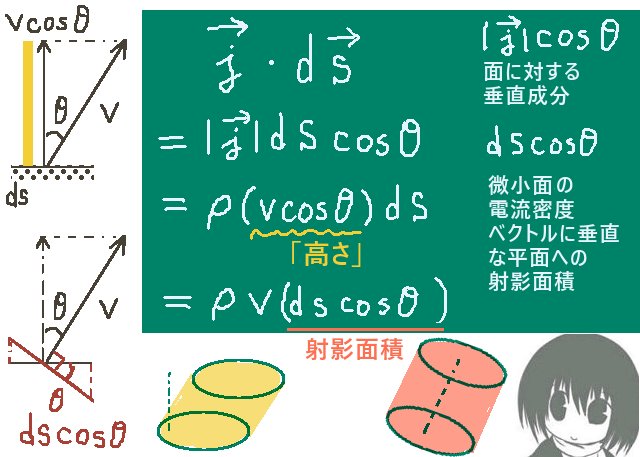
次に微小領域同士がなす角度θ(平面角の意味)は、
図の位置関係から\(\overrightarrow{r}\)と曲面S上の面積要素ベクトル\(d\overrightarrow{s}\)のなす角に等しくなります。
(面積要素ベクトルは曲面上の微小領域に垂直です。)
曲面S上の微小領域の面積を\(|d\overrightarrow{s}|\) =dsとして
球面上の微小領域の面積をdAとおくと、dA=dscosθです。
他方で\(\overrightarrow{r}\)と\(d\overrightarrow{s}\)の内積を計算すると\(\overrightarrow{r}\cdot d\overrightarrow{s}\)=r ds cosθ=r(ds cosθ)=rdAです。
そのため、今考えている微小領域に対する立体角の微小量をdΩの定義式から計算すると次のようになります。【途中で分子に対してr(ds cosθ)の形を作る変形をしています。】
$$d\Omega =\frac{dA}{r^2}=\frac{rdA}{r^3}=\frac{rds\cos\theta}{r^3}=\frac{\overrightarrow{r}\cdot d\overrightarrow{s}}{r^3}$$
そこで、曲面Sの領域全体に対して微小領域を合計して分割の極限をとる事で法線面積分の形になります。(dΩを同じ領域で積分すると、曲面S上の分割と球面上の分割は1つ1つ対応させているので全体の立体角Ωとなります。)
$$\Omega=\int_S\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}$$
\(\overrightarrow{r}\)/(r3)は、-1/rに対する勾配ベクトルを使って-grad(1/r)とも書けます。
閉曲面の場合には開曲面を2つ考えてつなぎ合わせる事により、
表と裏の関係による符号にだけ注意すれば同じように関係式が成立します。
同時に、ここでの導出での途中式で得られている関係式も
物理的な考察に使える事があります。
$$d\Omega =\frac{dA}{r^2}=\frac{ds\cos\theta}{r^2}$$
導出ではこれを内積として考えて法線面積分ができる形にしていますが、
これをそのまま使える場合というのもあります。
発散定理から考える方法
曲面Sの外縁の閉曲線の各点から原点Оに向かって直線を引いて錐面を作り、原点は曲面Sの裏側のほうに位置しているとします。球面は原点を中心とします。原点と曲面の間のてきとうなところで球面を考えて、「開曲面Sと錐面と球面上領域Sc」で構成される閉曲面S0を考えます。
すると原点から向かう位置ベクトル\(\overrightarrow{r}\)は、その閉曲面上では曲面S上で表側を向き、球面上では裏側を向きます。つまり同じ被積分関数\(\overrightarrow{r}\)/(r3)に対する法線面積分は符号が互いに逆になります。
原点を中心とする球面上では球面に対して\(\overrightarrow{r}\)は垂直なので各微小領域で\(\overrightarrow{r}\)/(r3)と面積要素ベクトルとの内積は1/(r2)とdsの積です。球面上で1/(r2)は一定値である事に注意すると、法線面積分は定数をS=0から「表面積の値」まで積分したものになります。
そこで球面上領域Scの面積を4πr2kとおくと、Sc上の法線面積分は、閉曲面S0では裏側で行う事にも注意して-4πk(=-Ω)となります。
$$\int_{Sc}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_{Sc}\left|\frac{\overrightarrow{r}}{r^3}\right|ds=\int_{Sc}\frac{1}{r^2}ds=\frac{1}{r^2}\int_{Sc}ds【S_c 上でrは一定値なので】$$
$$=-4\pi r^2k\cdot\frac{1}{r^2}=-4\pi k$$
また錐面は\(\overrightarrow{r}\)の定数倍の線分で構成される微小平面の集まりなので、各微小領域で面積要素ベクトルは\(\overrightarrow{r}\)に垂直です。よって、錐面での\(\overrightarrow{r}\)/(r3)の法線面積分は0になります。
ここで、ガウスの発散定理を使うために
\(\overrightarrow{r}\)/(r3)に対する発散(無限大の発散ではなく div のほう)を考えると次の公式がつかえます。
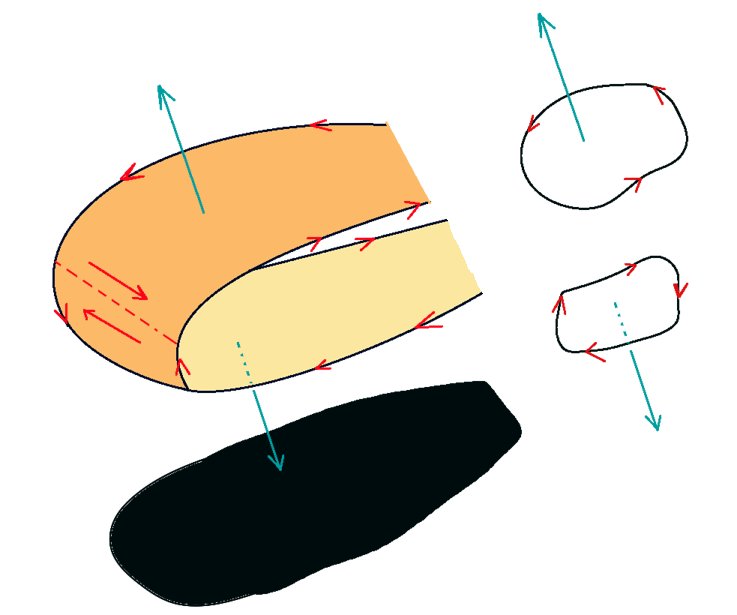
ベクトル場に対する発散 div の直接計算により次式が成立します。 $$\mathrm{div}\left(\frac{\overrightarrow{r}}{r^3}\right)=0$$ ベクトル場の発散 div\(\overrightarrow{F}\) はスカラー量です。
そこで、ガウスの発散定理を使うと次式が成立します。
$$\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_V\mathrm{div}\left(\frac{\overrightarrow{r}}{r^3}\right)dv=0【発散定理より】$$
$$他方で、\int_{S0}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\int_{S}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}-4\pi k$$
$$よって、\int_{S}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}-4\pi k=0\Leftrightarrow\int_{S}\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=4\pi k=\Omega$$
Sを閉曲面として考える場合には原点ОからSに向かって引いた直線でSに接するものを考えます。接点で構成される閉曲線によりSを2分割して錐面と球面上の領域を含めた全体の領域を考えれば、その内部にある開曲面上の法線面積分は表と裏で合計するとプラスマイナスが打ち消して0になるので上記と同じく開曲面Sに対しての考察で関係式を導出できます。

\(\overrightarrow{r}\)/(r3)に対する発散の計算は上図のようになります。当サイト他記事より内容を引用。
円錐の半頂角と立体角の関係式
円錐があった時に、円錐の頂点から見た時の円錐の広がりを表す立体角はどれほどになるでしょうか。これは「底面の中心を含む円錐の断面に等しい三角形を考えた時に、斜辺を半径として円錐の頂点を原点とする球が円錐の底面の周によって切り取られる領域の表面積はいくらですか」という問題です。
円錐の場合には立体角以外にも半頂角(これは平面角)を使う事でも広がりを表現できます。
半頂角とは、
「円錐の頂点と底面の中心を含む断面の三角形における円錐の頂点を含む角度の半分」です。
半頂角の大きさを弧度法で表してφ【rad】であるとして、立体角との関係式を作る事ができます。
底面の中心を含む円錐の断面に等しい三角形を考えた時に、
斜辺の長さをrとして、半頂角の大きさをφ【rad】とすると
円錐の頂点から見た立体角は次のように表されます。
$$\Omega=2\pi (1-\cos\varphi)【sr】$$
rは円錐の底面の円周上の点から頂点までの距離でもあり、また円錐の頂点から見た立体角を考える時の球の半径としても特に扱います。(立体角を考える球の半径は任意ですが、一番計算しやすい半径としてここでのrを使います。)
この式でφ=π/2(これは半頂角の値で、2倍するとπです)とおくと
半球分の表面積をr2で割った値となり、半球分の立体角を表します。
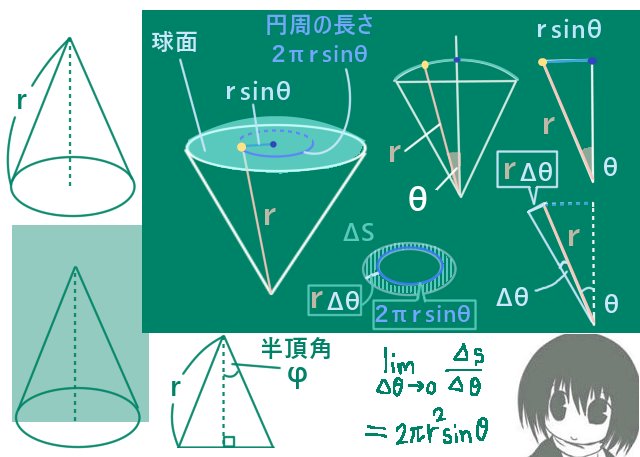
この式は図形的な考察と積分(1変数の)によって導出します。
底面の中心から球面上に直線を引き、円錐の高さとなっている線分とのなす平面角をθとします。底面の中心から球面上までの長さを保ったまま直線を回転させると球面上に円ができます。この時に円錐の頂点と底面の中心を含む断面ではθの値は同じです。円錐の頂点からその円までの範囲の面積をSとするとそれはθの1変数関数S(θ)です。円錐が作る立体角はΩ=S(φ)/(r2)です。
ΔS=S(θ+Δθ)-S(θ)とすると、
図形的な考察によりΔS≒(rΔθ)・(2πrsinθ)であり、
ΔS/ΔθはΔθ→0の極限でr・(2πrsinθ)=2πr2sinθと表せます。
そこで、逆に2πr2sinθを積分すればS(θ)が得られるはずで、
定積分すればS(φ)が得られるはずであるという流れです。
【より詳しくは (rΔθ)・2πrsinθ ≦ ΔS(θ) ≦ (rΔθ)・2πrsin(θ+Δθ) となり、
変形すると2πr2sinθ ≦ ΔS(θ)/Δθ ≦2πr2sin(θ+Δθ) となるのでΔθ→0として、
sin(θ+Δθ)→sinθとなる事に注意して導関数(微分)がdS/dθ=2πr2sinθのように表せると考えます。すなわち、1変数の定積分および微積分学の基本定理の考え方です。】
rΔθは円弧の長さ(直線状の線分の長さに近似)を計算していて、
ΔSの面積の部分の「幅」でもあります。
2πrsinθはS(θ)の表面積の領域の外周である円周の長さです。
この時にはθを積分変数として区間を[0,φ]のもとで積分をすると表面積に等しくなります。(この場合はこの計算で球の表面積の一部分を表せるという事であり、一般の曲面の表面積はより複雑です。)この積分でθの関数になっているのはsinθの部分だけになります。
$$S(\varphi)=\int_0^{\varphi}2\pi r^2\sin\theta d\theta=-2\pi r^2\large{[\cos\theta]_0^{\varphi}}=2\pi r^2(1-\cos\varphi)$$
立体角はS(φ)/(r2)なので式からはrが消えて次式になります。
(Ωはrに依存しないはずなので、その事とも合っています。)
$$\Omega=\frac{S(\varphi)}{r^2}=\frac{2\pi r^2(1-\cos\varphi)}{r^2}=2\pi (1-\cos\varphi)$$
例1:立体角による電場に関するガウスの法則の理解
電場に関するガウスの法則(ガウスの発散定理とは関係はあるけれども別物)は、電荷が作る電場の大きさが距離の2乗に反比例する事に由来して数式的にはガウスの積分の形をしています。さらに法線面積分を考える対象が閉曲面であり、電荷が閉曲面の内部に含まれる考え方としては「立体角は4πになるので」という事で直ちに法則の結果を得るというわけです。
Q【C】の電荷を囲む閉曲面Sに対して、電荷が作る電場に関して次の法則が成立します。
(ε0は真空の誘電率)
$$\int_S\overrightarrow{E}\cdot d\overrightarrow{s}=\frac{Q}{\epsilon_0}$$
この式は「法則」なので(定理ではなく)そのまま受け取ればいいのですが、
この法則の場合は数式的に左辺が右辺に等しい事を見るために考察ができます。
電場ベクトルは大きさがQ/(4πε0r2)【1/(4πε0)はクーロン力の比例定数】であり、
向きは電荷の位置を原点とした時の単位位置ベクトル\(\overrightarrow{r}/r\)です。
【\(\overrightarrow{r}/r\)は、ベクトル(x.y,z)をrで割って大きさを1としたもの】
それをもとに書き直すと、法則の左辺は立体角に対する定数倍の形で表せます。
具体的に法則の左辺をQやrの形にすると次のようになります。
$$\int_S\overrightarrow{E}\cdot d\overrightarrow{s}=\frac{Q}{4\pi\epsilon_0}\int_S\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}$$
つまりガウスの積分の定数倍という事になりますが、前述の考察によりそれは閉曲面に対する立体角と同一視する事もできるわけです。
そしてここでは電荷の位置(原点)は閉曲面の内部にあるので「積分の値は4π」であると考えれば、定数であるQ/(4πε0)に乗じる事で法則の右辺の形Q/ε0を直ちに得れるという見方もできます。
$$\int_S\overrightarrow{E}\cdot d\overrightarrow{s}=\frac{Q}{4\pi\epsilon}\int_S\frac{\overrightarrow{r}}{r^3}\cdot d\overrightarrow{s}=\frac{Q}{4\pi\epsilon_0}\cdot4\pi=\frac{Q}{\epsilon_0}$$
これは計算としてはガウスの積分を使った場合と同じになります。
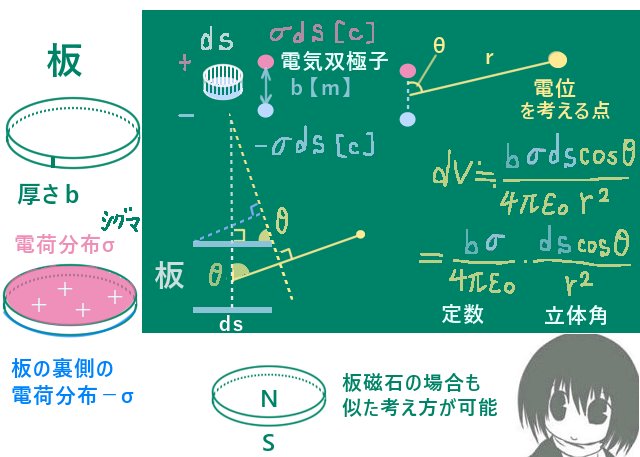
例2:電気二重層が作る電位
薄い導体板の片側に一様プラスの静電荷が一様な大きさで分布していて、その裏側ではマイナスの静電荷が一様な大きさで分布している電気二重層が作る電位は立体角を使って表現できます。
導体板の厚さがb【m】で、板の表側の表面電荷密度がσ【C/m2】(>0)であり
裏側の表面電荷密度が-σ【C/m2】であるとして、
導体板内には電荷は存在せず、真空の誘電率はε0とします。
この時に板から離れた点(板の厚さに比べて十分離れた位置)Pから板に向けて考えた立体角をΩとすると、点Pでの電位は次のように表されます。
$$V=\frac{b\hspace{1pt}\sigma\hspace{1pt}\Omega }{4\pi\epsilon_0}【V】$$
この式で、より具体的にはΩは別途に計算される必要があります。
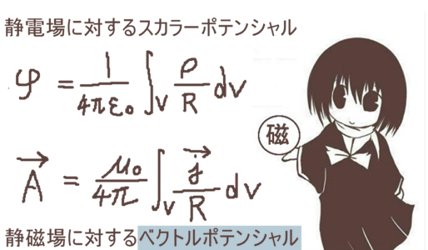
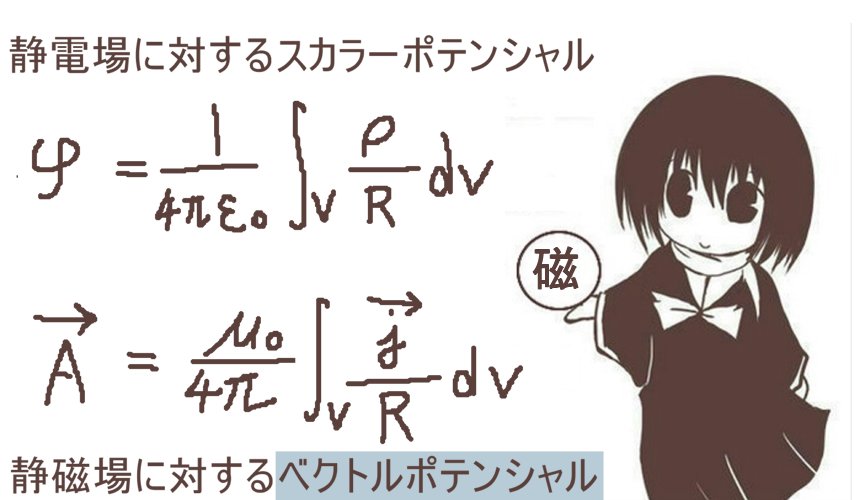
考え方としては板磁石や、環状電流が作る磁場で電流が作る磁場の渦が十分弱いとみなせる位置において便宜的な量である「磁位」の計算する事にも使えます。
この関係式は板の表と裏に電気双極子(互いにわずかに離れた位置にある同じ大きさの電気量で存在するプラスとマイナスの電荷)が分布していると考えて、板の微小な部分が作る電位を計算すると点Pから見た微小面積に対する立体角の定数倍となる事から導出されます。
互いにb【m】離れている+Q【C】と-Q【C】があり、
電荷の中点からr【m】離れていて2つの電荷を通る直線とのなす平面角がθの
位置Pでの電位を考えると、bに比べてrが大きければ次の近似式が成立します。
$$V=\frac{b\hspace{1pt}Q\hspace{1pt}\cos\theta}{4\pi\epsilon_0r^2}【V】$$
単独の点電荷が作る電位はrに反比例するという結果なので、電気双極子の場合にはrの2乗に反比例するという結果が得られる所が異なります。
この式は単独の電荷が作る電位を合計して(差の形になりますが)、rがbに比べて十分大きいという近似のもとで平方根を一般二項定理により展開する事で得られます。
板の微小面積がdsの部分による点Pに作る電位dVを、電気双極子が作る電位とみなして計算します。プラスとマイナスの電荷の大きさはσdsで、電荷の距離は板の幅でdです。
$$dV=\frac{b\hspace{1pt}\sigma \hspace{1pt}ds\cos\theta}{4\pi\epsilon_0r^2}=\frac{b\hspace{1pt}\sigma}{4\pi\epsilon_0}\cdot\frac{ds\cos\theta}{r^2}=\frac{b\hspace{1pt}\sigma}{4\pi\epsilon_0}d\Omega$$
ここで行ったのは定数となる部分と立体角の微小部分dscosθ/(r2)を見やすくするために分けた事と、前述の考察による微小面積部分におけるdΩ=dscosθ/(r2)を代入した事になります。
ところで分割を十分細かくとったうえでdΩの合計をとると立体角Ωとなるわけですが、ここで考えている電位はスカラー量であり単純に加える事で合計の電位となるのでdV=kdΩの形の量を十分細かい分割のもとで合計すればVが得られます。すると板全体では、ここでは実はV=kΩを意味します。
$$分割を十分細かくした極限で合計してV=\frac{b\hspace{1pt}\sigma\hspace{1pt}\Omega}{4\pi\epsilon_0}$$
ただし先ほど触れた通り、より具体的に計算をするには板の形状などを指定したうえでΩの具体的な値の計算が必要です。