カテゴリー: 高校数学

直交座標上の直線

恭平

直線と１次関数の関係・用語・公式を説明します。

これは中学校でも扱われますが、ここでは高校数学の範囲の事も説明します。

目次：

  1. 直線を表す式
  2. 応用問題①：平面上での「平行」と「直角」の式での表し方
  3. 応用問題②：他の図形と組み合わせる問題

直線は１次関数になり、放物線は２次関数になります。３次関数や４次関数は、微分を使って形を考察するのが普通です（従って微分を使わない範囲では原則として問われません）。

■高校数学としての難易度：この分野の理屈はそれほど難しくはないので、センター試験程度の問題であれば誰でも満点を狙える分野です。ただし、公式を暗記しようと思うと苦しくなるところでもあります。
式と図形がどのように対応するのか、意味を理解して素早く式を組み立てる事が得意になるためのポイントの１つかと思います。一度式を作れば、あとは式変形を繰り返して図形と対応させていくだけです。

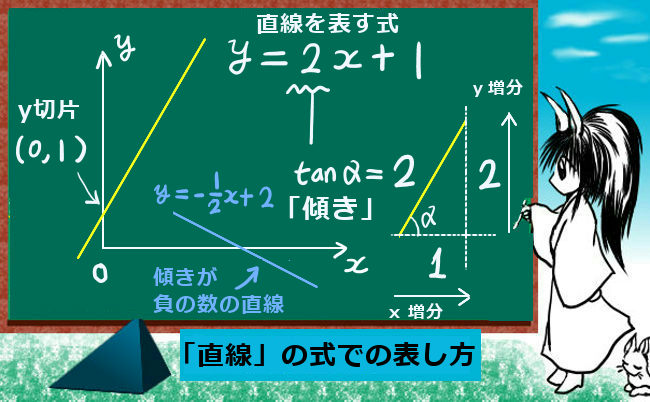
直線を表す式

■ 直線を表す式は１次関数　■ ２点を通る直線の式　■ １点を通る直線の式　

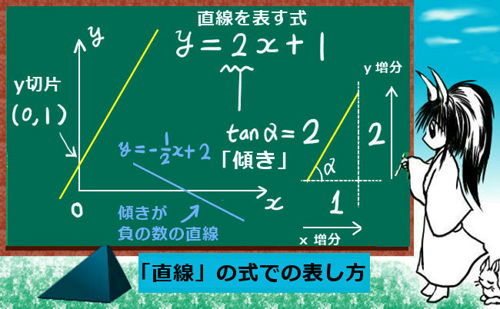
直線を表す式は１次関数

直線は、１次関数で表されます。つまり、ｙ = ２ｘ や ｙ＝３ｘ＋１のような形の式です。

ｙ =２ｘの「２」のように、ｘにくっついている比例定数の部分を「傾き」と呼びます。図形上で見た時、その部分が実際に傾いている度合いを表すためです。ｙ＝３ｘ＋１の「１」のように完全に定数になっている部分を「切片」または「ｙ切片」などとも言います。これは、その値がｙ軸（ｘ＝０を表す直線）でのｙの値を表すためです。

「傾き」は、プラスである場合も、マイナスである場合もあります。直交座標上のグラフだと「右上がり」の形の直線です。直交座標上のグラフで言うと「右下がり」の形の直線になります。

尚、傾きが０の直線はｘ軸に平行な直線で、ｙ＝３のような式です。ｙ＝０は、ｘ軸に他なりません。
逆にｘ＝３のような式はｙ軸に平行な直線になります。この場合には傾きが「無限大」という事でもありますが、傾きとしては「表せない」と考える事が普通です。ｘ＝０を表す直線はｙ軸そのものです。

また、高校数学の場合には図形上の角度を使って「傾き」をタンジェント（正接）で表す事もできます。図形と式の問題と見せかけてじつは三角比や三角関数の問題という事もあり得るので、一応知っておくべきでしょう。

一次関数
高校数学の場合、一次関数が図形上の直線の性質とどう対応するのかを数式で表現する事が重要です。座標、図形上の角度、他の図形との組み合わせ、三角関数やベクトルと組み合わせた色々な出題が考えられます。

２点を通る直線の式

高校数学の場合、座標上のてきとうな２点があって、それを通る直線の式はどのようになるかという事を計算させる問題があります。

その式の表し方は、一応「公式」があって教科書にも書いてあると思うのですが、
これは「意味は理解すべきであるが暗記はすべきでない」公式の１つです。

公式？（正しい式ではある）

$$２点(x_1,y_1)(x_2,y_2)を通る直線の式は次式で表せる：$$ $$y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)$$ $$あるいはy-y_2=\frac{y_2-y_1}{x_2-x_1}(x-x_2)でも同じです。$$

☆POINT：まず最初にこの式を暗記しない事
この式は結果としてはそうなるという式であって、最初から丸暗記する事で問題を解くものではないのです。逆に意味を理解しててきとうにいくらか練習をすれば、この式を自然に書く事もできるようになるのです。

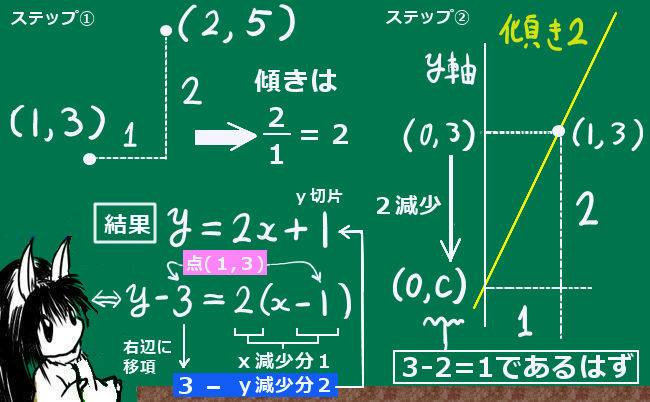
２点を通る直線の式
図形的な意味を把握してから、覚えられるのであれば公式のような形で覚えるとよいと思います。上記の「公式」では、少なくとも傾きの部分は式を覚えるのではなく図形的に把握したほうが早いと思われます。それ以外の部分は、分かりやすいほうで理解したほうがよいと思います。

まず、てきとうな２点があったとして（１,３）と（２,５）だったとしましょう。図に書くと分かりやすいのですが、まず「傾き」を計算します。これは単純な話で、「ｘの増分で、ｙの増分で割ったもの」（それが図形上は正接であるわけですが）を計算すればよいのです。ここでの場合、２になります。

公式に当てはめているのではないのです。
ｙの増分：５－３＝２　ｘの増分：２－１＝１
という計算を（頭の中で）しているだけなのです。

$$この時点で、y=2x+C\hspace{5pt}の形の式になる事が分かります。$$

「では、ｙ切片の情報はどうやって知るのですか。」

これも図に書くと分かりやすいのですが、ｙ切片（０,C）から点（１,３）までのｘの増分は、もちろん１です。点（１,３）から見ると、ｙ切片（０,C）に至るまでにｘは１減少します。

ｙの増分は、傾きが分かっているので、点（１,３）から見てｘが１減少するのであれば、ｙは１×２＝２減少します。・・という事は、点（１,３）のｙ座標から逆算すれば、ｙ軸上の点は３－２＝１ということになり、これがｙ切片であるＣの値なのです。

上記の「公式」は、じつはこの操作をしているのと同等の式なのです。ｙ軸から１つの点のｘ軸までの距離に傾きをかけ、その値を点のｙ座標から差し引く事でｙ切片を出すのと同等の式であるという事です。。

$$結果：y=2x+1$$

図形的に意味が把握できているのであれば、機械的に手早く計算するために上記の「公式」を１点（Ａ,Ｂ）を使って「ｙ－Ｂ＝(傾き)・(ｘ－Ａ)」として覚えてしまってもよいでしょう。覚え方としては「ｘ＝Ａ、ｙ＝Ｂ を代入すると確かに成立する」のような感じでもいいと思います。

ただし最初からそのように丸暗記するのではなく、まずは図形的な意味を理解する事がおすすめです。

正答率を上げるには、間違いがないかチェックする事も大事です。２点（１,３）と（２,５）を通るわけですから、値を代入してみて等式が成立するかを見ます。

$$2\cdot1 +1=3,\hspace{10pt}2\cdot 2+1=5$$

このようになるので、確かに合っている事が分かります。

全て頭の中で計算できるなら一番それが速いのですが、この手の問題は図形的な意味との関連が問われる事も多い都合上、ごく簡単なものでよいので図を描いて解いたほうが無難かもしれません。

１点を通る直線の式

直線がある１点だけを通る事が分かっている場合、もちろんそのような直線は無数にあり、それだけでは直線を表す式も決定しません。

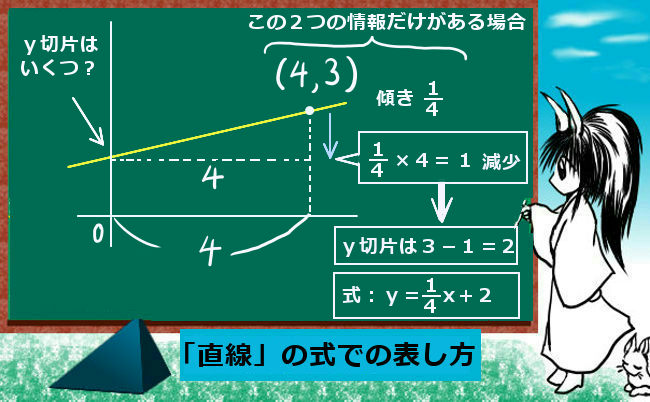
この場合は、ある１点の座標を（Ａ,Ｂ）傾きをＴ、ｙ切片をＣとすると式を次のように書けます。

$$y-B＝T(x-A)\Leftrightarrow y=Tx+B-AT$$

$$C=B-AT$$

この式も、ある点から点（Ａ,Ｂ）までのｙ座標の増分とｘ座標の増分の関係を表しているだけなのです。決して、暗記すべきような公式ではありません。

（ｘ－Ａ）がｘ座標の増分、それに傾きＴを掛けるとｙ座標の増分（ｙ－Ｂ）です。ｙ切片については、（０,Ｃ）と（Ａ,Ｂ）の間の増分の関係を見ればよいのです。ｙの増分：Ｂ－Ｃ　ｘの増分：Ａ－０＝Ａ　ですから、ＡＴ＝Ｂ－Ｃであり、変形すると上記のようにｙ切片であるＣを表す事ができるのです。

図に描くと分かりやすいでしょう。

１点を通り傾きが分かっている直線の式
１点を通る事と傾きの値だけが情報として分かっている場合の計算です。

この場合もやはり式を暗記するのではなくて、図形と対応させて意味を理解したうえで、式自体もすぐに書けるように練習しておく事が得意になるポイントの１つです。

応用問題①：平面上での「平行」と「直角」の式での表し方

■ 平行の表し方　■ 直角の表し方

平行の表し方

２つの直線が平面上で平行になる場合、直角になる場合など、より図形的な直線の状況を表すために式を計算させる問題も存在します。

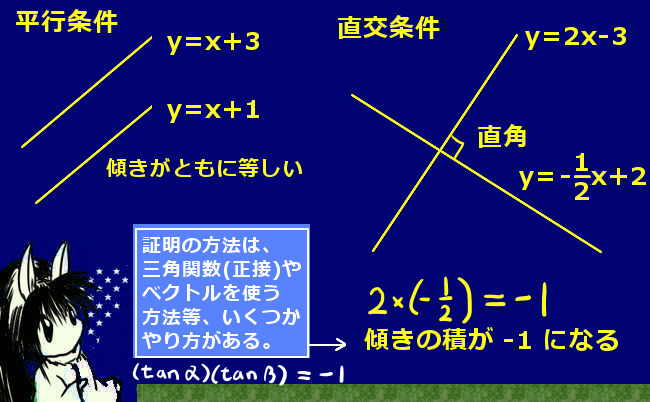
まず平行の場合ですが、これは簡単で、「傾きが等しい」直線同士は直交座標上で平行になります。もちろん、それでｙ切片も同じであれば全く等しい直線ですから、異なる平行２直線であれば「傾きは等しくｙ切片は異なる」という条件になります。

平行という事は、もちろんそれら２直線は交わらないという事です。式で見た時には、連立方程式にしてみるとｙ切片が異なる値の時は２式を同時に満たす（ｘ,ｙ）の組は存在しないという事でもあります。一応、その事も念頭に置いておくとよいかもしれません。

直線の平行条件と直交条件
平行・直角に交わるという平面上の２直線に関する様子を、傾きが満たす条件で表す事ができます。

直角の表し方

次に直角の場合です。２直線が交わり、なす角が直角であるという場合です。この場合は、「傾き同士の積が－１」になります。こういうものに関しては、１つの「公式」として結果を把握しておいたほうがよいと思います。

公式：直交する２直線の傾き

直交する２直線の「傾き」同士の積は、必ず－１になる。

この「直線同士が直交」する事に関して、高校数学での出題としては図形に対する接線と法線の関係は問われやすく、特に円に対する接線と法線の関係にも注意しましょう。図形問題としてだけでなく、それを式で表現させるという出題が高校数学ではなされる場合があります。

証明：直交する２直線の「傾き」同士の積は－１である

もちろん、傾きの積がー１になれば直角であるという事は、自明ではありませんね。そもそも、個々で言う「直交する」事が図形的な意味で使われているので、これを式ではどう考えるのかを解釈する必要があります。

証明の方法はいくつかありますが、ここでは三角関数を使う方法とベクトルを使う方法を紹介します。

三角関数を使う場合、傾きはタンジェントで表せる事を上記で軽くふれましたが、これを利用します。

【証明①：三角関数を使う方法】

$$\tan \alpha \tan \beta=\frac{\sin \alpha}{\cos \alpha} \cdot\frac{\sin \beta}{\cos \beta}=\frac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}$$

$$\alpha -\beta=90° ならば\cos (\alpha -\beta)=0より、\cos \alpha \cos \beta+\sin \alpha \sin \beta=0\Leftrightarrow\cos \alpha \cos \beta=-\sin \alpha \sin \beta$$

$$したがって、\tan \alpha \tan \beta=\frac{\sin \alpha \sin \beta}{-\sin \alpha \sin \beta}=-1【証明終り】$$

べクトルを使う場合は、２直線の交点から直線上の（任意の）点までのベクトルを考えて、内積が０であるして計算します。

【証明②：ベクトルを使う方法】

２つの傾きをＳ，Ｔとします。（Ａ,Ｂ）からのｘ座標の（任意の）増分Ｘを考えて（Ａ＋Ｘ,Ｂ＋ＳＸ）と（Ａ＋Ｘ,Ｂ＋ＳＴ）を考えます。これらは直線上の座標点でもありますが、ベクトルとしても考える事ができるのです。

ベクトルとして考えた時、直交するという条件は「内積が０」という条件になります。

この時、内積をとるベクトルは（Ａ＋Ｘ,Ｂ＋ＳＸ）－（Ａ,Ｂ）＝（Ｘ,ＳＸ）と（Ａ＋Ｘ,Ｂ＋ＴＸ）－（Ａ,Ｂ）＝（Ｘ,ＴＸ）です。（ベクトルの考え方で言うと、原点に平行移動させて考えてもよいという事です。）

内積を計算すると、直交する条件のもとでは

$$(X,SX)\cdot(X,TX)=0\Leftrightarrow X^2+STX^2=0\Leftrightarrow X^2(1+ST)=0$$

この式が任意のＸについて成立するには１＋ＳＴ＝０⇔ＳＴ＝－１
すなわち、直交する２直線の傾きの積はー１になるという事です。【証明終り】

参考までに、平行や直角ではなく、特定の３０°とか４５°で直線同士が交わるという条件が仮に問われた場合は、傾きをタンジェントで表して、三角関数の加法定理で対応するという手法を使えます。これについてもベクトルを使う方法、あるいは複素数を使う方法等、手法はいくつか考えられます。

応用問題②：他の図形と組み合わせる問題

高校数学の範囲ですと、放物線であるとか円であるとかいった他の図形と直線の関係を問う問題があります。これは、何点で交わるかとか、直線が他の図形の接線になる条件は何か等を問う類のものです。

放物線や円の場合、直線の式とそれらを連立させて、二次方程式を作らせる問題が典型的です。その二次方程式が重解を持つ場合は１点のみで交わる接線という事になり、異なる２つの実数解であれば２点で交わり、異なる２つの複素数解の場合には直交座標上で「交わらない」という事になるのです。

「ある１点を通って、かつ円に接する２直線の式は何か」といった類の問いの場合は、前述の１点を通る直線の式と円を表す式を連立させて条件を調べるといった具合の解法になります。

接線について問う問題の場合、微分が使える場合もあります。センター試験の場合は微分の知識がなくても解ける問題しか出題されませんが、問題によっては通常のやり方と微分によるやり方の２通りで解く事で、解答が正しいかのチェックなどに使える場合もあります。

サイト内関連記事【高校数学で扱う関数】

ベクトルの内積

恭平

ベクトルの内積についての説明をします。

内積の定義には２通りの方法がありますが、
計算によって２つの定義は同等のものである事を証明できます。

目次：

☆参考：ベクトルとスカラー（初歩的なベクトルの考え方や表記方法など）

ベクトルは大きさと向きを持った量であり、加算、減算、定数倍、内積
の演算が定義されます。

内積の定義①：成分を使う定義

ベクトルに対して定義される重要な計算規則として、「内積」があります。

これは「２つのベクトルの各成分同士の積を加え合わせる」という演算です。
数学的には何次元のベクトルでも定義する事ができます。

ベクトルの成分はスカラーですから、成分同士の積を合計するともちろんスカラーです。
つまり、ベクトルの内積の計算結果は必ずスカラーになります。

この内積の計算は物理学への応用で重要です。 具体的には、仕事とエネルギーという、物理や工学の基礎となる理論の形成に用います。ベクトルの微積分にも直接関係します。また、電磁気学等でも使う接線線積分、法線面積分の定義にも直接的に関わるものになります。

ベクトルの内積の定義 ２つのベクトルの「『各成分の積』の和」を内積と言います。
記号は、「・（ドット）」を用いて、\(\overrightarrow{A}・\overrightarrow{B}\) のように書きます。 $$２次元：\overrightarrow{A}・\overrightarrow{B}=a_1b_1+a_2b_2 $$ $$３次元：\overrightarrow{A}・\overrightarrow{B}=a_1b_1+a_2b_2+a_3b_3 $$ $$ｎ次元：\overrightarrow{A}・\overrightarrow{B}=a_1b_1+a_2b_2+a_3b_3+a_4b_4+\cdots+a_nb_n $$ $$=\sum_{j=1}^n a_jb_j$$ ★ 上述の通り、ベクトルの内積は、スカラー量です。つまり通常の実数などの値になります。
★ ベクトルの内積は、必ず２つのベクトルについて計算されるもので、３つ以上のベクトルの内積というのは考えません。
★ 数学的には、じつは内積はもっと抽象的ないくつかの演算条件を満たす計算であると定義されますが、このページの内容にはあまり関係ないので記載は省略します。
内積は、「２つ」のベクトルに対して定義される演算です。
３つ以上のベクトルに対する内積といものは定義されません。
その理由は、２つのベクトルの内積はスカラーである事にもよります。

内積の計算を行う事を、習慣的に「内積をとる」という表現で表す事も多いです。

内積は必ず２つのベクトルに対して考えるものですが、内積自体は「スカラー量」であるという事は、理論が色々と複雑になってくる時に重要になってきます。

内積の定義②：余弦（cosΘ）を使う定義

さて２次元の平面ベクトルや３次元の空間ベクトルの場合、
じつは余弦定理を使う事によって内積は図形的な意味も持つようになります。
物理では、こちらの形式での内積の表現も結構重要です。

具体的には、２つのベクトルの内積は「２つのベクトルの大きさと『なす角の余弦(cosΘ)』の積」に必ず等しくなります。
こちらのほうを内積の定義とする場合もあります。

平面や空間において、物理で内積が重要になるのは、この図形的な意味によるところが大きい場合が多いのです。

ベクトルの内積の別の表現 $$２次元：\overrightarrow{A}・\overrightarrow{B}=a_1b_1+a_2b_2=|\overrightarrow{A}||\overrightarrow{B}|\cos \theta $$ $$３次元：\overrightarrow{A}・\overrightarrow{B}=a_1b_1+a_2b_2+a_3b_3=|\overrightarrow{A}||\overrightarrow{B}|\cos \theta $$ ★ ｎ次元の場合でも新たに「角度」とその余弦を（半ば無理やりに）定義すれば数学的には一応同じ事が言えます。
ベクトルの内積の表し方は２つの方法がありますが、物理で使う時は両方の表し方が重要です。平面や空間での図形的な考察をする時は余弦 cosθ を用いる表し方が重要であり、式変形や計算を進める時は成分による表し方を用いる事が多いです。
力学における「仕事とエネルギー」の関係は、内積とベクトルの微積分によって導出されます。

２つの定義が同等である事の証明

ベクトルの内積の定義には上述のように２通りあるわけですが、これらは数学的に同等のものです。すなわち、どちらで計算したとしても全く同じ値になります。
（ただし次元の数が４以上の場合は、余弦を改めて定義しなければいけません。）

２つの定義が同等のものであるという事は、もちろん自明ではありません。
証明が必要です。

しかしその証明は難しくなく、
余弦定理を使って余弦を成分で表し、丁寧に計算すると示せます。

☆余弦定理は、鋭角・鈍角三角形の辺の長さの関係を三平方の定理によって表現する事で得ます。
参考：直角三角形の辺の比の関係・・・余弦 cosΘについての初歩的な解説があります。

\(|\overrightarrow{A}-\overrightarrow{B}|=c\)とします。
これは２つのベクトルが作る三角形の斜辺です。
余弦定理（任意の角度で成立）により、
$$c^2=|\overrightarrow{A}|^2+|\overrightarrow{B}|^2-2|\overrightarrow{A}||\overrightarrow{B}|\cos \theta$$ $$\Leftrightarrow |\overrightarrow{A}||\overrightarrow{B}|\cos \theta=\frac{1}{2}(|\overrightarrow{A}|^2+|\overrightarrow{B}|^2-c^2)$$ ですので、余弦を使った定義による内積は次のように表せるわけです。 $$\overrightarrow{A}・\overrightarrow{B} =|\overrightarrow{A}||\overrightarrow{B}|\cos \theta =\frac{1}{2}(|\overrightarrow{A}|^2+|\overrightarrow{B}|^2-c^2)$$ $$=\frac{1}{2}\left\{(a_1^2+a_2^2+a_3^2)+(b_1^2+b_2^2+b_3^2)-(a_1-b_1)^2-(a_2-b_2)^2-(a_3-b_3)^2\right\}$$ $$=\frac{1}{2}(2a_1b_1+2a_2b_2+2a_3b_3)=a_1b_1+a_2b_2+a_3b_3【証明終わり】$$ 途中で成分がたくさん出てきますが、２乗の項は＋－を差し引いて全て消えてしまうので、成分同士を乗じたものの和になるという結果が得られるわけです。

補足：内積に対して「外積」とは？

補足として、ベクトルの外積についてここで定義だけ簡単に記します。

内積と同様に、ベクトル同士に対して定義される計算規則ですが、外積は３次元の空間ベクトルのみに対して定義されます。そこが内積と異なる点です。ベクトル積、クロス積などとも言います。

外積は物理での応用で重要です。角運動量を論じる時や、電磁気学などで用いたりします。３次元的な直交する方向同士の関係を適切に表すために有効な計算方法です。

２つのベクトル\(\overrightarrow{A},\overrightarrow{B}\) の外積 \(\overrightarrow{A}×\overrightarrow{B}\) は、次のような３次元空間のベクトルとして定義されます。

  • 大きさは、\(\overrightarrow{A}と\overrightarrow{B}\)　が作る「平行四辺形の面積」 （※平行四辺形の面積をベクトルで表す公式があり、内積の計算も関係します。）
  • 向きは、\(\overrightarrow{A}と\overrightarrow{B}\)　の両方に垂直で、\(\overrightarrow{A}から\overrightarrow{B}\)に（１８０°以下の角度の方向に）向かって右ねじを回した時に、ねじ回しが向いている方向

外積の「向き」については、文章だとちょっと分かりにくいと思いますが、要は、１つの平面に対して垂直な向きは２方向考えられるのですが、そのうちの１方向だけを必ず指定できるようにするためにこのような定義をしています。


この外積の考え方は、基本的に高校では使わないと思います。また、物理学を学ぶ時にはベクトルの外積は非常に重要ですが、他の工学等を学ぶ場合にはそれほど重要でないという場合もあります。
これはなぜかというと、物理学で外積を使う主な理由は角運動量や電磁気力の位置関係を３次元的に捉えるのに有効な計算方法であるためで、言い換えるとそれらを扱わない場合にはそれほど多く使う計算ではないとも言えるからです。

初等関数の微分公式

恭平

この記事では初等関数の微分公式とその導出・証明をまとめています。ここで扱う初等関数は主に単項式、三角関数、指数関数、対数関数を主に指します。（逆三角関数は別の記事で詳しく扱っています。）

■関連サイト内記事：微分についての定義や定理、関連する事項などです。

初等関数の微分公式の一覧表

基本となる初等関数の微分公式

初等関数について、微分演算によって得られる導関数のうち、
最も基本的なものと思われるものをまとめると次のようになります。

関数名式導関数備考
定数関数ｙ＝ｃｙ’＝０定数に対する微分は０になります。
単項式ｙ＝ｘaｙ’＝aｘa－１aは実数で、ｙ＝１／ｘや
ｙ＝\(\sqrt{x}\) を含む
正弦関数ｙ＝sinｘｙ’＝cosｘ４回微分するともとの式に戻る
余弦関数ｙ＝cosｘｙ’＝－sinｘ４回微分するともとの式に戻る
指数関数ｙ＝ eｘｙ’＝eｘ自然対数の底 e を使った場合。
もとの関数と導関数が一致。
対数関数ｙ＝ lnｘｙ’＝１／ｘ自然対数関数の場合。（底が e）

「単項式」とは２次関数や３次関数がｘaの形で単独で存在しているものを指し、それを定数倍と和や差で組み合わせると「多項式」になります。
定数関数については単項式で指数が０の場合と考えても可です。定数関数の微分が０になるという事は、要するに普通の１とか２とかの定数を微分すると結果は必ず０であるという意味です。

単項式の導関数について代表的なものをいくつか挙げると次のようになります。

a単項式導関数備考
a＝１ｙ＝ｘｙ’＝１２階微分は０
a＝２ｙ＝ｘ２ｙ’＝２ｘ２階微分は定数
a＝３ｙ＝ｘ３ｙ’＝３ｘ２３次関数のグラフの
形状に関係
a＝－１ｙ＝１／ｘ
　＝ｘ－１		ｙ’＝\(-\frac{\Large 1}{\Large x^2}\)
　＝－ｘ－２
ｘ＝０で微分不可能
（関数を定義できない）
a＝－２ｙ＝１／(ｘ２)
　＝ｘ－２		ｙ’＝\(-\frac{\Large 2}{\Large x^3}\)
　＝－２ｘ－３		ｘ＝０で微分不可能
（関数を定義できない）
a＝１／２ｙ＝\(\sqrt{x}\)
　＝ｘ１／２		ｙ’＝\(\frac{\Large 1}{\Large 2\sqrt{x}}\)
　＝(1/2)ｘ－１/２
ｘ＝０で微分不可能
（導関数を定義できない）

その他の初等関数の微分公式

次に、その他の初等関数の微分公式です。
これらは、基本となる微分公式から導出できるものが少なくありません。

関数名式導関数備考
正接関数ｙ＝tanｘｙ’＝１／(cos２ｘ)
　＝１＋tan２ｘ		正弦、余弦の微分公式と
積・商の微分公式から
指数関数
（一般）		ｙ＝aｘｙ’＝(ln a)aｘe 以外の指数関数
対数関数
（一般）		ｙ＝ logaｘ
＝(lnｘ)／(ln a)		ｙ’＝１／(ｘln a)e 以外の底。
底の変換公式使用
逆正弦関数ｙ＝Arcsinｘｙ’＝\(\frac{\Large 1}{\Large \sqrt{1-x^2}}\)マイナス符号をつけると
逆余弦関数の導関数
逆正接関数ｙ＝ Arctanｘｙ’＝\(\frac{\Large 1}{\Large 1+x^2}\)積分で理論上
重要な場合がある
双曲線関数ｙ＝ \(\frac{\Large e^x-e^{-1}}{\Large 2}\)
　＝sinhｘ
ｙ＝ \(\frac{\Large e^x+e^{-1}}{\Large 2}\)
　＝coshｘ		(sinhｘ)’＝coshｘ
(coshｘ)’＝sinhｘ		三角関数の導関数の
関係に似ている。
（微妙に違う。）

微分の公式と接線の傾きの関係

初等関数の微分公式は、基本となる単項式・三角関数（特に正弦と余弦）・指数関数・対数関数に限って言えば比較的平易な形をしているとも言えます。

と言ってもプラスとマイナスの符号の関係など、細かい部分は混乱する事もあるかもしれません。そのような時には、関数のグラフの接線の傾きとしての微分係数を考えてみると理解に役立つ場合があります。

関数のグラフを描いてみて、接線の傾きが正（グラフで言うと右上がり）、負（右下がり）、０、無限大など、見て大体分かる部分があるので、微分の公式の導関数との対応を考えると比較的分かりやすいです。

対数関数などは、 微分して得る導関数は 1／x ですが、ｘ がゼロに近づくにつれて無限大の急な傾きになっていく事が表現されています。また、逆に x を無限大にしていくと傾きはどんどん緩やかに０に近づいて行く事になります。

x = 0 付近で傾きが非常に急で無限大に近く、x の値が巨大になるにつれて傾きが緩やかになり次第にほとんど０になるのは、「ｘの平方根」（ｘの１／２乗）などの関数でも同じです。

初等関数の微分公式の証明

微分の定義式からの個々の関数の微分公式の導出および証明を記します。

なるべく定義式からの極限として考えますが、
積の微分公式・合成関数の微分公式・逆関数の微分公式を途中で使ったほうがよい事もあります。（積の微分公式等はいずれも微分の定義式から導出されます。）

基本となる初等関数の微分公式は結果は比較的平易ですが、単項式で実数を指数とする場合の証明は意外と複雑だったり、三角関数に対しては計算を進めるうえで加法定理が必要だったりと、微分の定義から公式を導出する過程は意外と複雑であったりします。（そのため、微分を使っていくうえでは証明方法を理解したうえで「公式の結果は覚えてしまったほうが早い」とも言えます。）

単項式の微分公式の証明

定義式に直接単項式を代入すると、$$\frac{(x+h)^a-x^a}{h}$$となります。

他方で(x+h)a について、a が自然数 ｎであれば２項定理で展開する事によって$$\frac{nhx^{n-1}}{h}=nx^{n-1}$$の項だけが h→0 で 残り、他の項は全てゼロに収束します。

つまりｘ２の導関数２ｘや、ｘ３の導関数３ｘ２における、
２とか３とかの係数は２項展開した時の係数由来（ｎＣ１の項）であるというわけです。

しかしa が自然数でない場合には、少し証明に工夫を要します。
a が実数の場合でも「一般２項定理」が成立するのですが、その肝心の一般２項定理の証明が、一般的には単項式の微分の結果を使って行われます。（マクローリン展開を使います。マクローリン展開とは、微分を利用した関数の無限級数展開です。言い換えると微分の公式を必要とする展開です。）
そこで、単項式の微分公式の証明では、強引に一般２項定理の単独での証明を試みるよりは、
実は対数関数の微分を利用するほうが簡単です。

証明（a が実数の場合の単項式ｘaの微分公式）

対数の性質 ln xa=a ln x に注意して、$$\frac{d}{dx}(\ln x^a)=\frac{d}{dx}a\ln x=a\frac{d}{dx}\ln x=\frac{a}{x}$$ 他方で、合成関数の微分公式を用いると同じ式を別の形で表せます。
$$\frac{d}{dx}(\ln x^a)=\frac{\large{\frac{d}{dx}(x^a)}}{\large{x^a}}$$ という事は、$$ \frac{a}{x}=\frac{\large{\frac{d}{dx}(x^a)}}{\large{x^a}} $$ $$\Leftrightarrow {\large \frac{d}{dx}(x^a)=\frac{a}{x}x^a=ax^{a-1}}【ｈ→０】$$

指数関数の微分公式の証明

指数関数の微分は、e に関する微分公式の証明が基本になります。
証明の方法は、微分の定義式に直接関数を当てはめて計算を進める形になります。
その際に、指数と対数との関係を使って式変形をしていきます。

証明（e の指数関数の微分公式）

$${\large\frac{e^{x+h}-e^x}{h}=e^x\frac{e^h-1}{h}=e^x\frac{e^h-1}{\ln e^h}}$$

次に、eh－１＝ｋとおきます。$$e^h-1=k\Leftrightarrow\hspace{5pt}e^h=1+k\hspace{5pt}に注意して$$ $${\large\frac{e^h-1}{\ln e^h}}=\frac{k}{\ln (1+k)}=\frac{1}{\Large{\frac{1}{k}}\large{\ln (1+k)}}$$と表す事ができて、これの分母についてさらに$$\frac{1}{k}\ln (1+k)=\ln (1+k)^{\Large{\frac{1}{k}}}$$ という、e の定義式の形を含んだ式に変形できます。
h→0 の時k→0なので k に関する極限として考えてもよく、 $$\lim_{k \to 0}(1+k)^{\Large{\frac{1}{k}}}=\lim_{k \to \infty} \left(1+\frac{1}{k}\right)^k=e$$ なので $$\lim_{k \to 0}\frac{1}{k}\ln (1+k)=\lim_{k \to 0}\ln (1+k)^{\Large{\frac{1}{k}}}=\ln e = 1 $$ですから $$ \lim_{h \to 0}\frac{e^{\large{x+h}}-e^x}{h}=\lim_{k \to 0}e^x\frac{k}{\ln (1+k)} $$ $$=\lim_{k \to \infty}e^x\frac{1}{\ln (1+\large{\frac{1}{k}})^k}=e^x\frac{1}{\ln e}=e^x\frac{1}{1}=e^x$$

$$\lim_{n \to 0}(1+n)^{\Large{\frac{1}{n}}}=\lim_{n \to \infty} \left(1+\frac{1}{n}\right)^n=e$$ で定義される自然対数の底 （ネピア数）e が有限の値であるという事は、きちんと証明できます。少し面倒ではありますが自然数に関する２項定理を使って式を直接展開して、対象の式を数列として見た時に「上に有界である単調増加数列である」事を示す事で証明できます。e ＝ 2.718・・・である事はマクローリン展開を使うと見やすいです。

一般の指数関数の微分

一般の指数関数の微分については、定義に当てはめて自然対数の底の場合と全く同様にして計算を進めます。対数の底の変換公式により次のようになる事を使います。$$\log_a\left(1+\frac{1}{h}\right)^h=\frac{\large{\ln(1+\frac{1}{h})^h}}{\ln a}$$ $$これは、h → ∞ で\hspace{5pt}\frac{1}{\ln a}\hspace{5pt}に収束します。$$
微分の定義式による計算ではこの式が分母にありますから微分により得られる導関数は次式です。$$\frac{d}{dx}a^x=a^x\ln a$$

対数関数の微分公式の証明

直接定義から計算しても証明できますし、指数関数の逆関数が対数関数なので、逆関数の微分公式を用いても証明できます。いずれの方法でも、自然対数の底 e の定義式の極限値の存在が、対数関数の微分公式でも成立の根拠となります。

以下では微分の定義式から証明してみます。

証明（対数関数の微分公式）

$$\frac{\ln (x+h)-\ln x}{h}=\frac{\ln \large{\frac{x+h}{x}}}{h}=\frac{\ln \left(\large{1+\frac{h}{x}}\right)}{h}$$ $$=\frac{1}{x}\frac{x}{h}\ln \left(1+\frac{h}{x}\right)=\frac{1}{x}\ln \left(1+\frac{h}{x}\right)^{\LARGE{\frac{x}{h}}}$$ $$ \rightarrow \frac{1}{x}\ln e =\frac{1}{x} 【ｈ→０】$$

三角関数の微分公式の証明

三角関数のうち正弦関数と余弦関数の微分公式は、まず定義に当てはめて、sin(x+h) の形を三角関数の加法定理によって (sinx)(cos h) +(cosx)(sin h)の形にして計算を進めれば導出する事ができます。
ただし、計算の過程の最後で$$\lim_{h \to 0}\frac {\sin h}{h}=1$$の極限の公式が必要になります。（この公式は角度を弧度法で考えないと話が変になります。）

証明（正弦関数と余弦関数の微分公式）

■正弦関数 sin x の微分
$$\frac{\sin (x+h)-\sin x}{h} =\frac{\sin x \cos h + \cos x\sin h – \sin x}{h}$$ $$=\sin x \frac{(\cos h -1)}{h}+\cos x\frac{\sin h}{h} =-2\sin x \frac{\sin^2 \Large{\frac{h}{2}}}{h}+\cos x\frac{\sin h}{h}$$ $$\left(∵ \cos h-1=\cos^2\frac{h}{2}-\sin^2\frac{h}{2}-1=1-2\sin^2\frac{h}{2}-1=-2\sin^2\frac{h}{2}\right)$$ $$=-(\sin x) \sin \frac{h}{2}\frac{\sin \large{\frac{h}{2}}}{ \large{\frac{h}{2}}}+\cos x\frac{\sin h}{h}$$ $$ →\cos x【ｈ→０】\left(\lim_{h\to 0}\frac{\sin h}{h}=1より\right)$$ ■余弦関数 cos x の微分
$$\frac{\cos (x+h)-\cos x}{h} =\frac{\cos x \cos h – \sin x\sin h – \cos x}{h}$$ $$=\cos x \frac{(\cos h -1)}{h}-\sin x\frac{\sin h}{h}=-2\cos x \frac{\sin^2 \Large{\frac{h}{2}}}{h}-\sin x\frac{\sin h}{h}$$ $$\left(∵正弦の時と同じく \cos h-1=-2\sin^2\frac{h}{2}\right)$$ $$=-(\cos x) \sin \frac{h}{2}\frac{\sin \large{\frac{h}{2}}}{ \large{\frac{h}{2}}}-\sin x\frac{\sin h}{h}$$ $$→-\sin x 【ｈ→０】$$

正接関数の微分に関しては定義からも計算できますが、商の微分公式を使うほうがじつは簡単です。tanｘ＝(sinｘ)／(cosｘ) である事を利用します。

途中式にある(cosｈ －１）／ｈの極限計算は加法定理を使わない計算方法もあります。

$$\frac{\cos h-1}{h}=\frac{(\cos h-1)(\cos h+1)}{h(\cos h+1)}=\frac{\cos^2 h-1}{h(\cos h+1)}$$

$$=\frac{-\sin^2 h}{h(\cos h+1)}=\frac{-\sin h}{\cos h+1}\cdot\frac{\sin h}{h}\rightarrow 0\cdot 1=0【h\rightarrow 0】$$

(sin x)／x の極限問題

ここでは、円弧の長さを変数とする関数として正弦、余弦、正接を考えてみます。（それが弧度法の考え方そのものでもありますが、ここでは「角度」という語を使わないで考えてみます。）

その場合に余弦と正弦波は単位円の円周上の点のｘ座標とｙ座標として考える事ができますが、正接も相似な三角形の辺の比から tanｘ＝(sinｘ)／(cosｘ) としてきちんと考える事ができます。

この時に円弧の長さをｘとすると sinｘ＜ｘ＜tanｘが成立しますが、
より詳しく見るとsinｘは単位円に内接する正多角形の周の一部であり、
tanｘは単位円に外接する正多角形の周の一部です。
この図形的な長さの関係は、円弧および円周の長さを計算する時に使うものと実は本質的に同じです。
すなわち円の内接多角形と外接多角形の周の長さを考えて、角の数を増やした時の極限値として円弧や円周の長さを計算するやり方です。

それらの正多角形を正ｎ角形として考えた時、
内接する正ｎ角形については周の長さはｎについての単調増加数列となり、逆に
外接する正ｎ角形については周の長さはｎについての単調減少数列となります。
それらのｎ→∞の時の極限値として円弧の長さｘが存在します。
詳しく言えばそれは半径および直径に比例し、円周全体の場合の比例定数はπ（円周率）です。
そのため、任意の長さの円弧についてsinｘ＜ｘ＜tanｘが成立するというわけです。
（この図形的考察は、より詳細には三角不等式等を使って丁寧に見て行く必要があります。）

この時に内接・外接する正多角形の隣り合う頂点を結んだ円弧の長さｘは、ｘ→０となります。それが(sinｘ)／ｘの極限としてｘ→０を考える図形的な意味です。

sinｘ＜ｘ＜tanｘに１／(sinｘ)を乗じると、１＜ｘ／(sinｘ)＜１／(cosｘ) です。
ｘ→０で１／(cosｘ)→１なので、極限の性質によりｘ→０でｘ／(sinｘ)→１
(sinｘ)／ｘの極限はその逆数ですが、１の逆数なのでそのまま同じ１になります。
そのため、ｘ→０で(sinｘ)／ｘ→１という事になります。