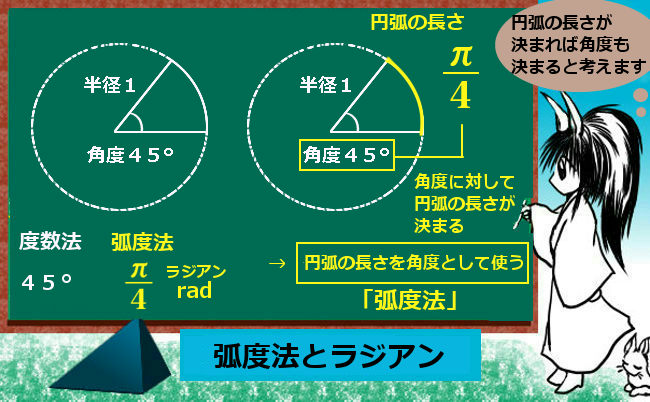
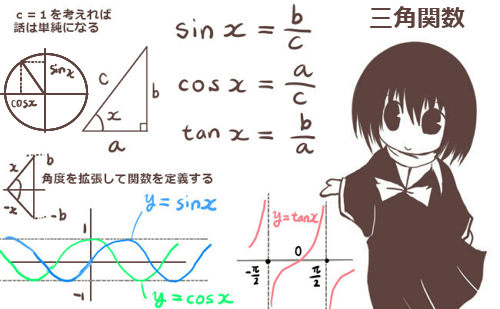
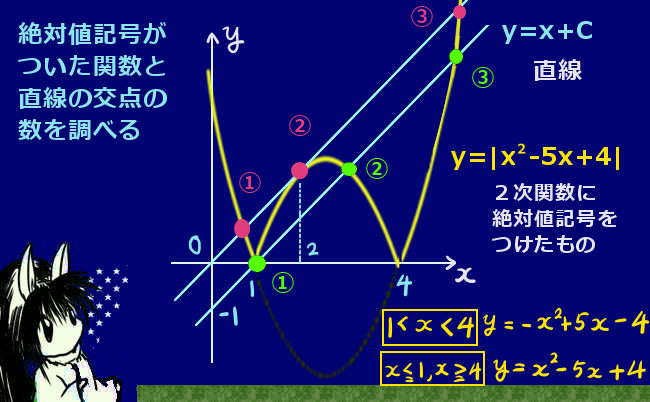
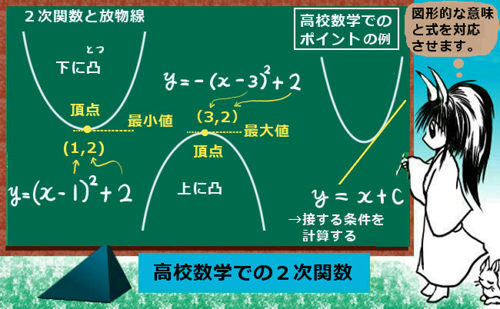
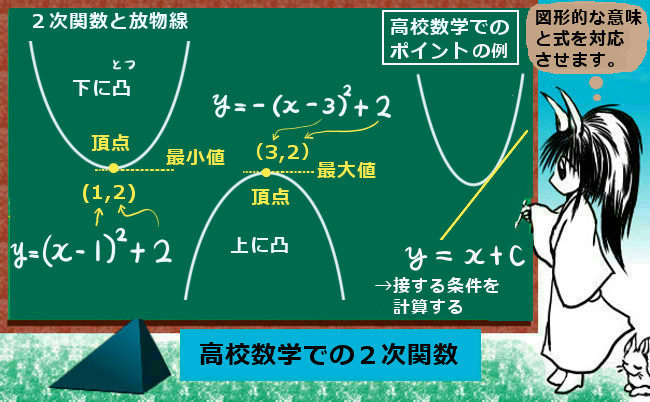
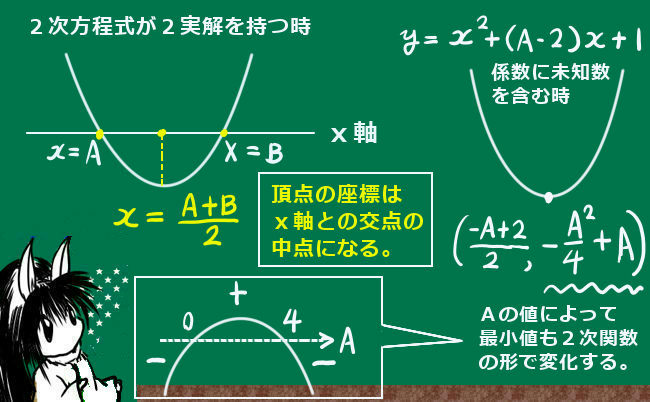
余弦定理とは、三角形の3辺と1つの角の余弦について成立する関係式です。
(英:cosine rule)
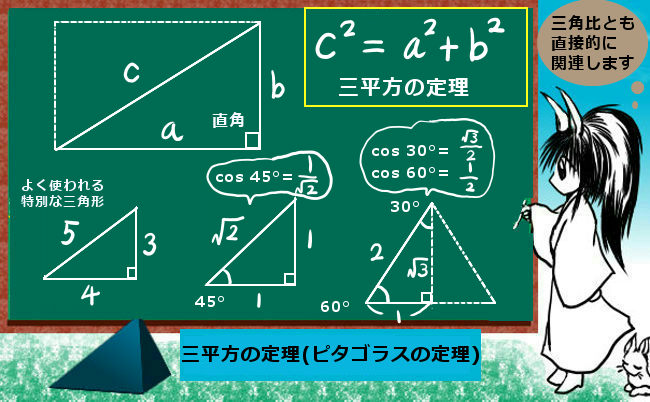
特別な場合として余弦定理を直角に対して適用すると三平方の定理の形になります。
(ただし、余弦定理一般を証明するには普通は三平方の定理を使います。)
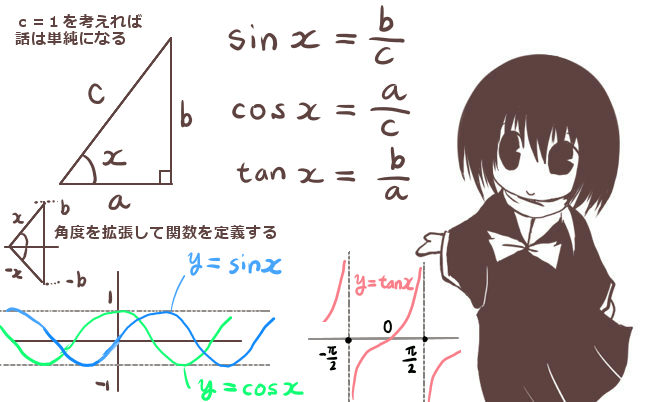
★三角比の余弦(コサイン)と三角関数の余弦関数については別途に述べています。
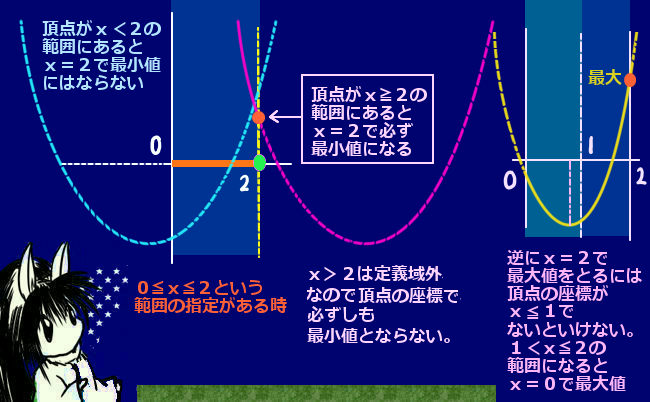
定理の内容
余弦定理の内容は次のようなものです。
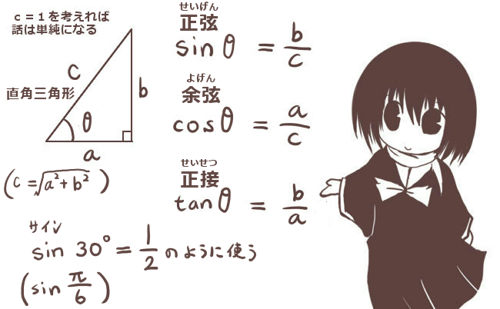
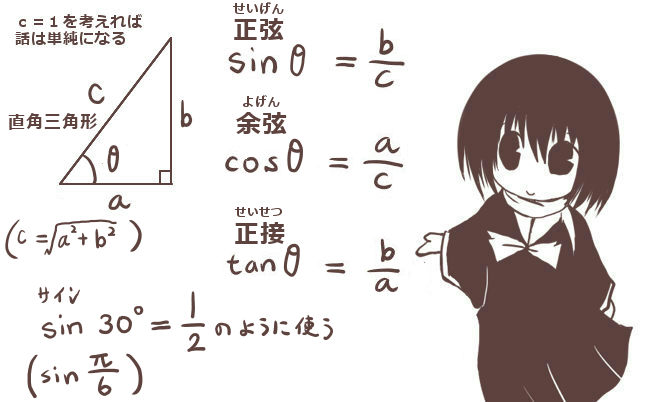
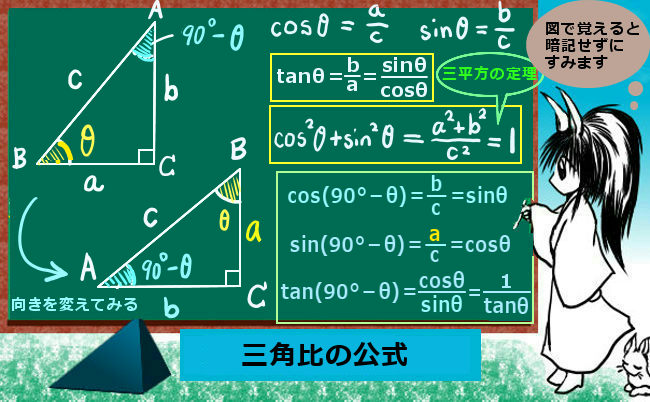
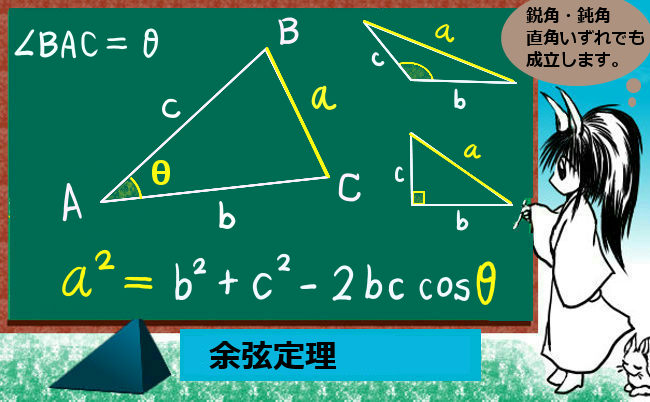
三角形ABCの辺の長さをBC=a、AC=b、AB=cとして、
∠BAC=θ(長さaの辺BCの対角)とする時、次の関係式が成立します。
$$a^2=b^2+c^2-2bc\cos \theta$$
θは鋭角でも鈍角でも成立し、
θ が直角の時には三平方の定理a2=b2+c2になります。
また、θ=0、\(\pi\)の場合は3点が1直線上に並んでいる場合であり、
座標上などで角度に向きをつけている場合には負の角度を代入しても正しい関係式を表します。
三角形のある1辺の具体的な値を知りたい時には「2辺の長さと1つの角度の『余弦』の値が分かれば計算は可能である」という事が、余弦定理の意味と使い方です。
余弦定理を証明する一番シンプルな方法は三平方の定理を使う方法です。(三平方の定理は相似条件・合同条件といった条件だけで証明できます。)
ここでは、対象の角の大きさが鋭角か鈍角で場合分けをして証明します。
式変形も含めてやや詳しく説明していますが、要するに三平方の定理を適切に適用すると関係式を導出できるというのが証明の流れになります。
証明①:鋭角の場合
まず対象の角度の大きさが鋭角の場合です。
この場合、もう1つの角についても鋭角か鈍角かで場合分けしますが、得られる結果は同じになります。どちらの場合でも、三角比の関係を使って上手に直角三角形の辺の関係を作ります。
下図で、∠BAC=θが鋭角のもとで、∠ABCが鋭角か鈍角かを見ます。
∠ABCが鋭角の場合(図の上側)、直角三角形を作るように線分ABを延長して点Hをとります。この時、直角三角形である△ACHの底辺部分AHの長さは余弦を使ってbcosθで表せます。
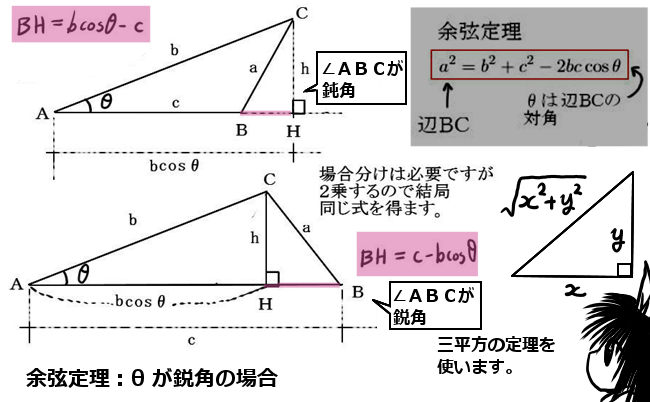
他方、高さ部分もCH=hは正弦を使ってh=bsinθと表せますが、単純にこれに三平方の定理を適用してもじつはうまくいきません。そこで、△ACHだけでなく、△BHCも直角三角形である事に注目します。すると、BH=bcosθ-cになる事に注するとうまくいきます。
BH2+h2=a2 ⇔ (bcosθ-c)2+h2=a2
他方、△ACHについてAH=bcosθ 、CH=hのもとで三平方の定理を適用します。
(bcosθ)2+h2=b2 ⇔ h2=b2-b2cos2θ
つまり、未知数のhは代入して消す事ができます。
(bcosθ-c)2+h2=a2 に h2=b2-b2cos2θを代入すると、b2cos2θ-2bccosθ+c2+b2-b2cos2θ=a2
⇔ a2=b2+c2-2bccosθ 【b2cos2θの項が消えてあとは順番だけ整理しただけです。】
つまりこの場合では余弦定理が確かに成立する事になります。
次に∠BAC=θと∠ABCが両方とも鋭角の場合(図の下側)には、点Cから辺ABに垂線を下ろせます。その垂線の足をHとおきます。この場合も先ほどとやり方自体は同じで、△AHCと△CHBの2つが直角三角形になり、CH=hとして余弦と組み合わせて三平方の定理で関係式を作ります。

AH=bcosθ、CH=h、BH=c-AH=c-bcosθ のもとで、
(bcosθ)2+h2=b2 かつ (c-bcosθ)2+h2=a2
前者のほうの式を後者のほうの式にh2を代入して消します。
(c-bcosθ)2+b2-(bcosθ)2=a2 ⇔ a2=b2+c2-2bccosθ
よって、この場合でも余弦定理が確かに成立する事になります。
証明②:鈍角の場合
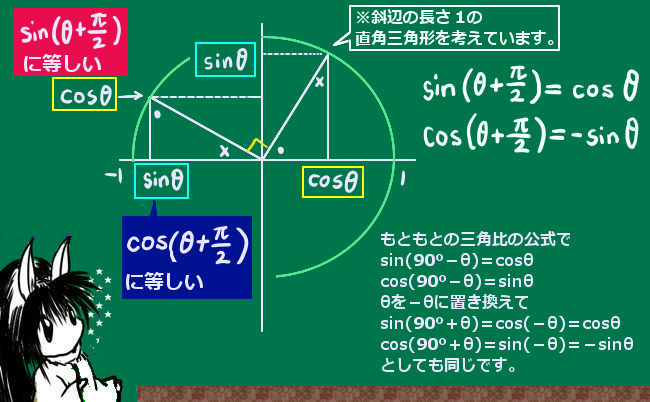
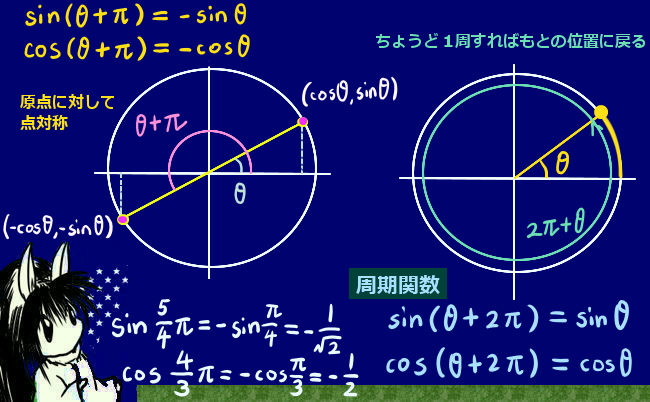
では、∠BACが鈍角の場合はどうするかというと、この場合には余弦に鈍角を入れる必要があるので三角関数として余弦を考える必要があります。結論を先に言うとcos(x+\(\pi\)/2)=-sinxの公式を使います。この関係を認めるうえで、余弦定理の形で辺の長さの関係を表せるという事です。
この時、鋭角である角度 φ を使って、θ = φ+90°と表すとこの時の証明はしやすいです。ただ、三角関数を使うので、ここで角度は弧度法で表してθ = φ+\(\pi\)/2と書く事にします。
この時、図のように△ABPが直角三角形になるように便宜上の点PをBC上において、∠ABPが直角、∠PBC=φ(鋭角)であると捉えます。(図の位置関係はθが鋭角の場合と少し変えて描いています。)
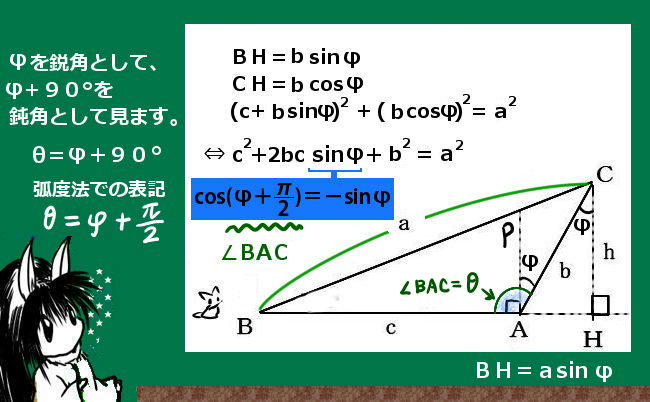
ここで、θ=∠PBC+∠ABP=φ+\(\pi\)/2です。この時、ABを延長しCからその延長線に垂線を下ろして垂線の足をHとします。
平行線の錯角の関係により∠BHC=∠PBC=φである事に注意し、△BHCは直角三角形なのでBH=bsinφ、CH=bcosφと表せます。ここで△AHCも直角三角形なので三平方の定理で関係式を作ると次のようになります。
(c+bsinφ)2+(bcosφ)2=a2 ⇔ c2+2bcsinφ+b2sin2φ+b2cos2φ=a2
ここでまず、sin2φ+cos2φ=1の公式により
b2sin2φ+b2cos2φ=b2(sin2φ+cos2φ)=b2
すると、c2+2bcsinφ+b2=a2
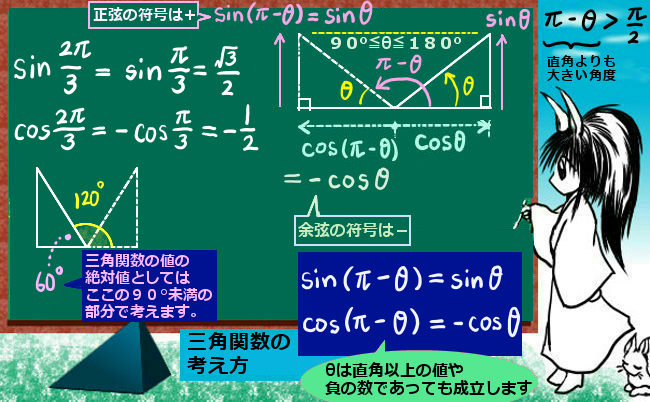
「余弦」定理の証明なのに正弦が出てきてしまったという話ですが、cosθ = cos(φ+\(\pi\)/2)=-sinφ つまりsinφ=-cosθとなるので、a2=b2+c2-2bccosθ となり、この場合も余弦定理が成立します。
これは三角関数の定義に従って余弦の値を決める時に成り立つもので、具体的な鈍角の値を余弦関数に入れると必ず負の値ですから、符号は必ず反転してプラスになる事に注意する必要もあります。
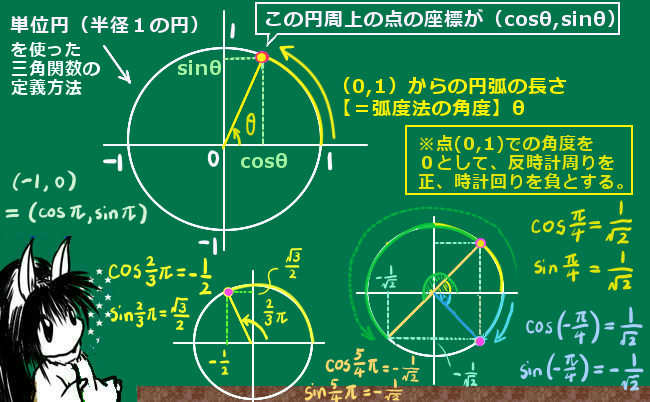
例えば120°(2\(\pi\)/3 [rad]) を角度として代入するなら、
a2=b2+c2-2bc・(-1/2)=b2+c2+bc のようになります。
理解の仕方としては、θが鋭角であろうと鈍角であろうと、三角関数の定義に従って余弦の値を考える限りは気にせずに余弦定理を使って計算をしてよい、という事になります。
角度の範囲が実数全体の場合
三角関数の定義域(実数全体)を当てはめるのであれば、上記以外の場合にはどうなるでしょう?
まず鋭角でも鈍角でもない角度として「直角」がありますが、これは冒頭でも触れた通り三平方の定理そのものになりますので、別途に証明できて成立します。
次に、0と180°(\(\pi\))の場合ですが、仮に成立するとすると次のような式になります。
θ=0とき、a2=b2+c2-2bc=(b-c)2 より、a=b-cまたはc-b
θ=\(\pi\)のとき、a2=b2+c2+2bc=(b+c)2 より、a=b+c
(もちろん、a≧0、b≧0、c≧0という条件のもとでこうなります。)
問題はこれに図形的な意味があるかという事ですが、じつは確かにあります。これらはいずれも、3点A、B,Cが一直線上に並んだ時にあり得る関係式です。そのため、これらの角度においては「三角形はできない」という図形的な意味付けをするのであれば、各点間の距離を表す式として余弦定理は確かに成立すると言えます。
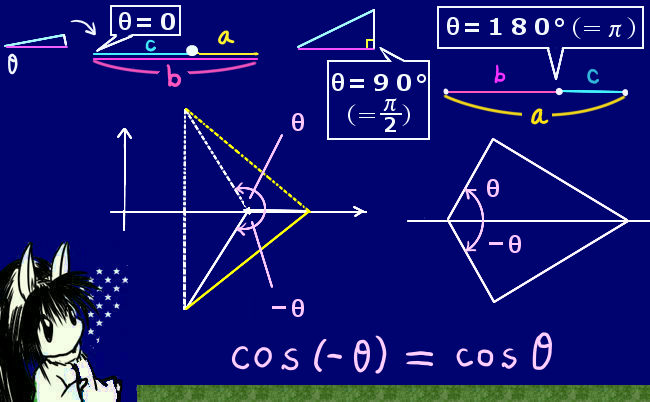
では、180°(\(\pi\))を超える場合はどのように考えられるでしょう。この場合、三角関数の考え方では負の角度が0~-\(\pi\)の場合と同じなので負の角度の場合を考えると、余弦関数の値はマイナス符号をつけない正の値の時と同じ値です。cos(-θ)=cosθと、三角関数では定義されます。
このような場合に図形上での意味としては、座標やベクトルの関係において角度に反時計回り・時計回りの区別をつける時の事が想定できます。しかしその場合でも「2点間の距離」自体は正の値として考えます。例えば座標上でx軸に平行な直線に関して図形を反転させた場合に、座標の符号が変わる事はあっても各点を結ぶ辺の「長さ」自体は変わりません。
この事が、負の値を角度として適用した場合の図形的な意味になります。0≦θ≦\(\pi\) の場合には余弦定理は適用可能ですから、-θを考えた時には cos(-θ)=cosθ により角度が正の値の時と全く同じ辺の長さの関係式になります。これが、「底辺を軸として三角形を反転させた時にも辺の『長さ』自体については変わらない」事に対応するのです。この意味において、座標上などで角度に向きをつける場合でも、辺の長さの関係だけを問題にする時には余弦定理に負の角度を入れても正しく関係式を作れるという事です。
★言い換えると、余弦定理だけからは「正負の符号も含めた」意味での座標の位置関係を確定させる事はできず、基本的には長さについてのみ計算可能な関係式であるとも言えます。これは三平方の定理と同様の性質です。
\(\pi\)を超える角度の図形的な意味は負の角度の場合と同じとすると、これも余弦定理の角度部分に代入しても三角形の辺の長さの関係は正しく表されている事になります。
三角関数の周期性により、360°(2\(\pi\))を超える角度では1周して全く同じ点に戻るという図形的な解釈のもとでは、それらの角度を代入したとしても同じく三角形の辺の長さの関係は同じく正しく表されます。
以上から、余弦定理は一般的な鋭角、鈍角、直角の三角形を考える場合にも、図形上の適切な意味付けを与える限りにおいては実数全体を余弦の角度として代入しても成立する関係式である、という事になります。