カテゴリー: 高校数学

数学の勉強方法【入試対策】

恭平 1件のコメント

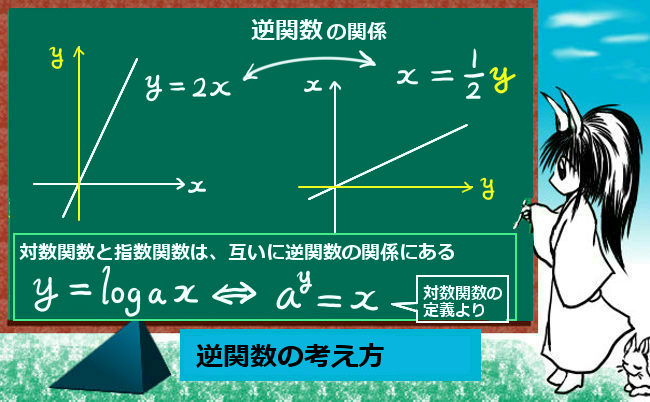
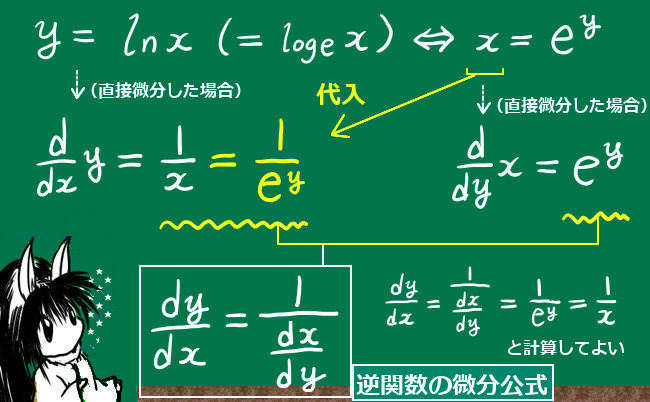
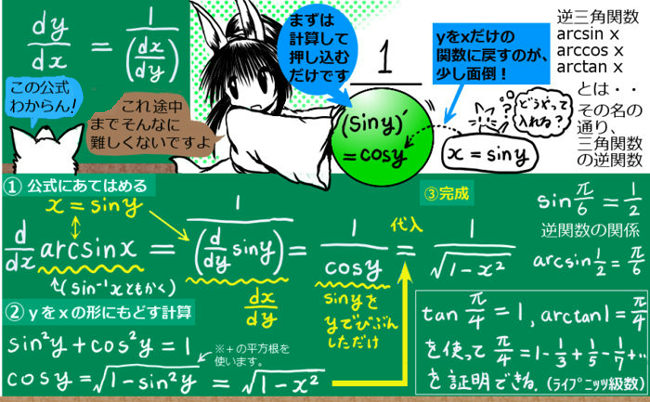
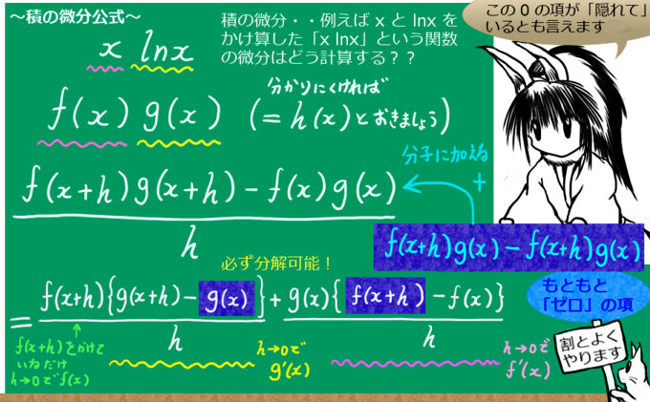
「学校での数学の勉強方法は、一体どうしたらよいか？」「数学の成績を伸ばすにはどうしたらよいか？」
こういった事はよく聞かれるので、中学や高校での実践的な勉強法について紹介します。

目次：

  1. 実践的な勉強法を知り、身に付けよう
  2. 中学校での勉強法
  3. 証明問題に対する勉強法
  4. 高校での勉強法
  5. まとめと結び

実践的な勉強法を知り、身に付けよう

よく耳にする「勉強方法」としては、授業の予習復習を欠かさない・１日１時間でも３０分でも勉強時間をとる・塾に通う・・等々というものです。これらについて私が聞いていて思うのは、科目の内容には直接的に言及しない一般論が極めて多いという事です。

それらの一般論は間違っているわけではありませんが、よい勉強方法というよりは「成績が良い子の特徴」を拾って列挙しているという面が結構強いのではないかと思います。もっと言うと、数学をあまり知らない人でも、成績優秀者にアンケート調査すれば分かる事を列挙しているようにも聞こえるのです。

よくある一般論的な「勉強方法」
  • 毎日の勉強時間の確保（例えば１時間でも３０分でも）
  • 授業をただ受けるのではなく予習と復習を必ずする
  • 塾や予備校に通う
  • 将来の夢を明確にする事で勉強への意欲を高める　等

→ 正しい事も言っているが「現に成績が良い子」の特徴の列挙にとどまっている面もあり、成績改善のための根本的な指南にはなりにくい。指摘の範囲が広すぎて具体性を欠いている事も否定できない。

それらの一般論が間違っているわけではなく、時に重要性もある事は強調したうえで、ここではより実践的で実際の数学にも踏み込んだ形でのおすすめできる「勉強方法」について紹介したいと思います。

ここで述べる事は、数学が得意でない人が成績を伸ばすために役立つ事でありますが、すでにある程度得意な人が成績に伸び悩み行き詰った時や、さらに上を目指したい場合にも役立つ方法です。（上記のような一般論だと、予習や復習はしているけれど成績が伸び悩んでいる人などは対処のしようがなくなってしまいます。）

実際に中学校や高校に通っていると勉強や進路に関して難しい事もあろうかと思いますが、まずは学校の数学の授業で教わっている内容が一体何なのかを把握しましょう。それが正直よく分かっていない状態で、「試験があるので公式だけは暗記する」・・というのは一番危険な勉強法です。これは中学でも高校でも、数学の勉強に関して共通に言える事なのです。

数学公式を覚えるために「語呂合わせ」（社会科だと『いい国【１１９２】作ろう鎌倉幕府』などが有名）を使う事を勧める人もたまにいらっしゃいますが、それを絶対否定はしませんが、その方法はどうしてもどうやっても覚えられない時の最終手段だと思う事をここでは勧めます。そうではない方法についてここでは述べます。

数学の成績を伸ばす手段の１つとして「多くの練習問題を解いてみる」という事は有効な方法です。ただし、それは基礎事項がある程度分かっている（完璧でなくても）時に先に進む手段として効力を発揮するもので、解き方の原理が全く分かっていない状態で練習問題に取り組んでも効果が薄いのです。

従って、数学があまり得意でない場合には、まず基礎事項を把握する事から始めるのが第一歩です。この時、公式だけを見て暗記しようとするのではなく、その公式の意味の説明や解説をよく読み、最初は自分で解かなくてもいいのでどういった計算例などがあるのかをよく見るようにしましょう。

完璧に理解してなくてもいいので、何となくでも分かったら、簡単なものからでよいので練習問題を解いてみてください。そして計算の方法などが分かってきたら、入試問題の過去問題を解いてみるなどしてレベルを上げて行きます。

中学・高校ともに共通する勉強法として大事な事は、わけもわからずに漫然と問題に手をつける事を繰り返すのではなく、基礎事項を理解したうえで問題を多く解くという事です。それによって、基礎事項の理解もより深まるのです。

個々の具体的な基礎事項を勉強する時には教科書や参考書を見てもいいですし、このサイトでは数学の基礎・重要事項についてイラストや図式も使いながら詳しく分かりやすく解説しています。

それらの押さえておくべき基礎事項を分野ごとに具体的に把握し、整理しておく事も重要です。これについては、中学数学・高校数学等に分けて次に具体的に記していきましょう。

★「基礎」とは必ずしも「簡単」という意味では無く、土台になる部分という事です。ただし中学校や高校の範囲では、基礎事項とは「まずは簡単な事項・初歩的な事項」というふうに捉えても差し支えありません。

中学校での勉強法

中学校の数学であれば、まずはマイナスを含んだ式の計算、文字式の展開、文字式の因数分解といったものを教わり、試験にも出題されます。（この試験とは期末試験などの校内のものも、高校入試も含みます。）

中学校の場合、公立の高校入試であれば（どの都道府県でも）おおよそ出題範囲は決まっており、おおよそ次のようなものです。

中学校の数学で扱う基礎・重要事項
  • マイナス符号の扱い（マイナス同士の掛け算など）
  • 文字式の展開と因数分解
  • 平方根の扱い（分母の有理化など）
  • 方程式（１次方程式、１次の連立方程式、２次方程式）
  • ２次関数と１次関数のグラフ問題（交点など）
  • 図形問題（作図、相似や合同の証明、辺の比・面積計算）【証明問題の勉強法については後述】
  • 初歩的な確率の問題（サイコロを２回ふるなど）
  • 統計（最頻値・中央値などの用語を把握したうえでのグラフの読み取り）
  • 立体に関する計算問題（展開図や平面での切り口）
  • 一部、自然数・整数に関する問題（約数、倍数、素数、個数の数え上げなど）

具体的な問題は、例えば次のようなものです。
「－２＋５はいくらか」「(－２)×(－３)＋１はいくらか」
「(ｘ－２)(ｘ－５) を展開しなさい」
「ｘ２－７ｘ＋１０を因数分解しなさい」
などのような問題が解ければ、身もふたもない事ですが「数学の成績が上がる」わけです。
※公立高校の入試の場合、多くの都道府県で求められるのはこういうレベルの計算です。ただし学校によっては入試でそれが「正確に」（速く）解ける事が求められます。

ここで、個々の生徒の人によって、問題を見て思う事が違うでしょう。
「暗算レベルですぐに答えられる」
「紙に書いて落ち着いて計算すれば解答を出せる」
「やり方は一応分かっているけれど計算間違いをよくしてしまう」
「そもそも何をどうすればよいのか分からない」

計算は人によって得意不得意あるので解けないからといって悪い事は何もないのですが、成績を上げるにはどうすればよいかという観点からは、まずは当人がどのような理解度にあるのかを把握する事が第一歩です。

これは、本人が自分で気づけば一番良いですが、それができない場合には大人が指摘してあげる事も大事なのです。実際、塾や家庭教師、通信教育の中には、そういった適切な指摘をしながら問題演習を通じて成績向上に導いていくという手法をとっている場合もあります。がむしゃらに問題を解かせるというのも成績向上の手法として否定はしませんが、それは前述のように、あらかじめ一定の理解度のある生徒にとってさらに成績を伸ばすために有効な方法です。

先ほどの問題ですが、－２＋５＝３ですが、これは結局５－２と同じで、
「足し算と引き算は本質的に順序を入れ替えてもよい」「引き算は『マイナスの数を加える』とみなしてよい」といった事が分かっている前提があるわけです。

次に (－２)×(－３)＋１＝７ですが、
これは「マイナス同士の掛け算はプラスになる」事と、
「掛け算と割り算は、足し算・引き算よりも優先して行う」という規則を知っているかを問うているわけです。つまり(－２)×(－３)を先に計算して６にする必要があるわけで、－３とその右隣の１を先に掛けたりしてはいけないわけです。【(－２)×(－３＋１）の場合には－３＋１を先に計算します。】

因数分解の問題の場合には、まずはその逆である式の展開について分かっていて計算もできる事が重要です。ｘ２－７ｘ＋１０＝(ｘ－２)(ｘ－５) ですが、これをすぐに計算できるようにするためには因数分解とは逆の
(ｘ－２)(ｘ－５)＝ｘ２－７ｘ＋１０ という式の展開計算が問題なくできるという前提があります。
そういった点を見落とさず、整理する事が基礎事項を押さえるという事の１つの具体例です。

大事なのは、まずは生徒である本人がそういった計算における「ルール」を正確に知っているかどうかです。知っているのであれば、あとはひたすら問題を多く解いて計算の精度と速さを上げていくという勉強方法は確かに成績向上につながります。しかし正直よく分かっていない状態で、なかば当てずっぽう的に問題を解く事を繰り返している状況になっている場合には一度立ち止まる事も必要です。

結果的に言えば、成績の良い子は多くの公式を暗記してるはずだと思います。しかしそれは、公式の意味や使い方は把握しているうえで、練習問題を通して慣れる事によって記憶を定着させている事が普通なのです。

あやふやな点がある・正直よく分かっていないところがあるという場合は、問題は解かなくていいので基礎にもどりましょう。そこで内容の理解に努めてから、簡単な問題からでいいので練習してみて、分かってきたら問題集や過去問によって速く・正確に解けるように繰り返し解いてみましょう。【速く解ける事は、見直しの時間を確保したり、多少手間がかかる出題があった時に落ち着いて考える時間を確保する事に役立ちます。】

高校入試の場合、公立高校やそれに準じるレベルの私立高校の場合は「難問・奇問」は出さず、基礎事項さえ正確に把握していれば確実に解けるレベルの出題をしている場合が大半です。一部の「難関私立校」を受験したいと思う場合でも、基本問題は確実に速く解けるという事はまず必要であり、そこからさらにやや難しい問題を解く練習を積む事が勧められます。

次に、中学校の数学の中でも「証明問題」に対する勉強はどのように考えたらよいのかについて、少し述べておきます。

証明問題に対する勉強法

中学校に入ると「証明」問題というものが出てきます。これは確かに、一見すると小学校の算数との大きな違いです。

中学校で証明問題というと大抵は図形問題かと思います。これを得意にするためには、基礎となる定理や条件を整理して理解したうえで、入試の過去問題や練習問題を繰り返し解いて練習してみる事が有効です。
ですから基本的には他の計算問題と勉強法は同じというわけです。

大事な事は、問題を一気に解決してくれるような裏テク的な「特別な定理」を探そうとしない事です。
最も基礎になる定理だけをまず理解して整理し、具体的な問題に使う時はどうすればよいのかを問題を解きながら理解し慣れていく事が大事です。

押さえておくべき基礎的な定理や図形の性質は、具体的には次のようなものです。

中学校の図形問題の証明で必要な事項

覚える事項をこういった基礎事項に絞ったうえで、練習問題や過去問題によって使い方を練習していくのが勧められる勉強法です。問題はいくらでも異なるものがありますが、大抵の場合はパターンが限られています。

一部の私立高校の入試などで他に事項が必要と思われる時のみ、過去問題を精査したうえで特別な定理を覚えればよいでしょう。もちろん、入試の受験などを抜きにして、平面幾何の分野に興味を持った場合に教科書に載っていない色々な定理を調べてみるという事は何ら悪い事ではありません。

証明問題について、「論述」をする必要があるという事で苦手意識を持つ人もいるかもしれません。しかし、数学の証明は国語の作文や小論文とは根本的に異なるものです。そのため普段の勉強においても、数学の証明は国語の問題や試験とは全く違うものである事をまずおさえておく必要があります。
数学の証明問題は、読み手を説得させる文章を書く事が目的ではなく、
「数学的に論理的に正しい関係をつなげて（決まった）結論を出す」というだけのものです。
ここで、「論理的に正しい」という事には文学的な意味も哲学的な意味もなく、要するに正しい計算をしているか・正しい定理の内容を書いているか・図形問題であれば正しい辺と角度の関係を書いているかという事なのです。

高校での勉強法

高校数学の場合、難関の国立大・私大の入試で「奇抜」な問題が出題される事があるのでその事に目を奪われがちかもしれませんが、中学校の場合と同じく基礎事項を整理し把握したうえで練習問題・過去問題を使って練習する事が最も勧められる勉強法です。高校の学内の期末試験等の対策も同じになります。

大学入試の場合には個々の大学によって出題傾向や難易度の差が激しい場合もあるので、確かにひとくくりにできない面はあります。しかし、基礎事項を正確に把握している事はどこの大学の入試でも求められます。したがって、普段の勉強でも特殊な問題や「難問」を無理に解く訓練をするのではなくて、まずは基礎事項を組み合わせて解ける問題を確実に解けるようにする事が勧められる勉強法です。つまり基本姿勢は中学校の時と同じでよいのです。

数学科目で高校が中学校と異なる点は、勉強する範囲が広いのでいきなり全ての対策を一度にはできない事です。範囲が広いので、場当たり的に勉強してしまうとつい学習が不足している部分が出てきやすいのです。分かりやすいところからでいいので、１つ１つの分野を確実に把握していく事が重要と言えるでしょう。

高校数学の微積分以外の分野で知っておくべき基礎・重要事項は次のようになります。

高校数学の基礎・重要事項
  • 直交座標上の図形と式（１次関数、２次関数、円、軌跡）【３次関数は主に微分の分野】
  • 数列（等差数列、等比数列、漸化式、階差数列、数学的帰納法）
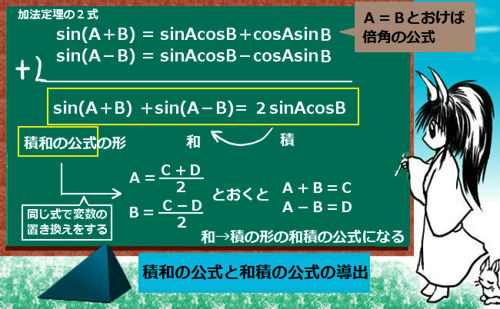
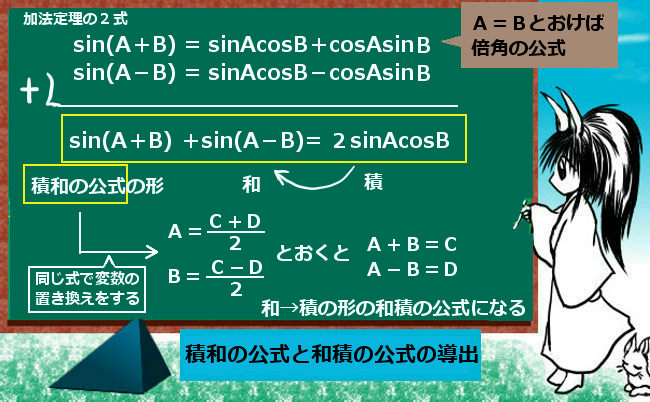
  • 三角比と三角関数（基本公式、弧度法、余弦定理、加法定理、極座標）
  • ベクトル（基本事項、内積、座標上の平行四辺形の面積など）
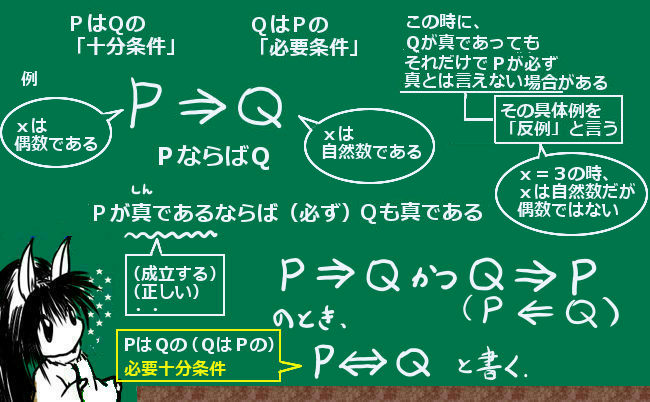
  • 集合と論理（包含関係、必要・十分条件、対偶証明法、背理法など）
  • 指数関数と対数関数
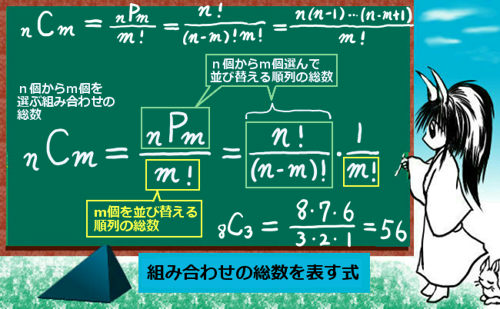
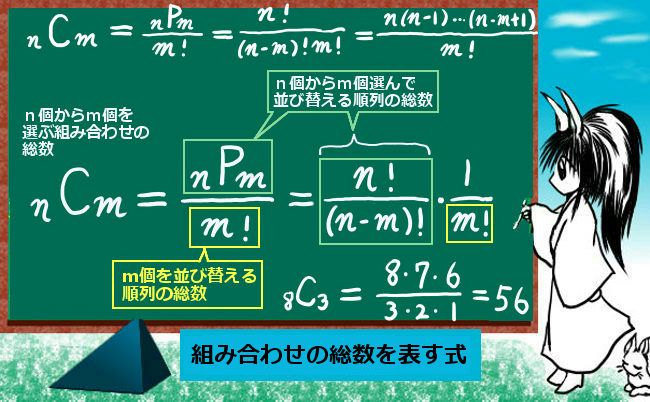
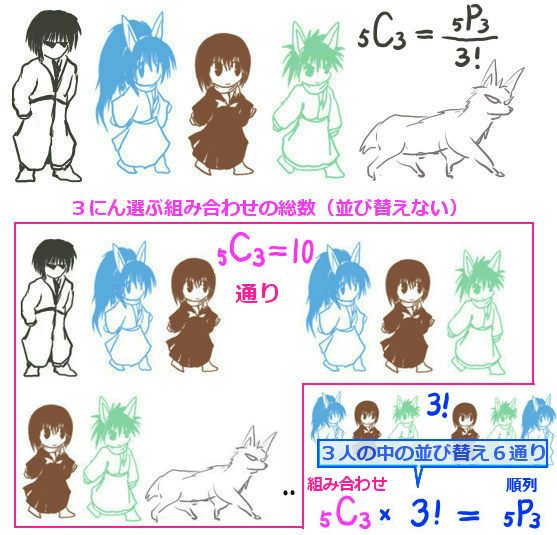
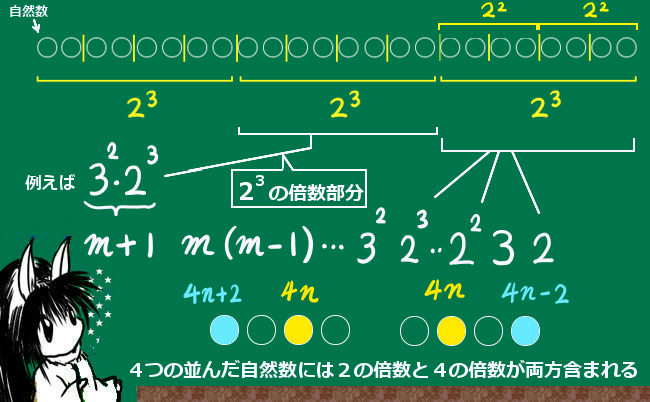
  • 場合の数と確率（順列、組み合わせ、条件付き確率、期待値、分散など）
  • 統計（中学よりも範囲が少し広い）
  • その他小さい事（絶対値記号、和の記号（Σ）、二項定理、解と係数の関係、部分分数、中間値の定理など）
  • 行列（基本的に２次の正方行列に関する出題が多い）
  • ２次曲線（楕円、双曲線、一般の放物線）

★高校の場合、立体に関する問題は積分で体積を計算させる出題が比較的多いです。
★様々な分野がありますが、最終的には全く別々の切り離されたものではなくて互いに関係しているという事を意識する事も重要かと思います。

高校数学では数学を授業科目として３～６つに分類する事が多いですが、学習時にはあまりこういう分類にはこだわらずに「微積分」と「それ以外」くらいの分類の認識でもよいかもしれません。微積分の問題を解く場合にはそれ以外の事項の基礎知識が欠かせない場合も多いので、まずは「微積分以外」の分野をしっかり勉強しておく事が重要とも言えます。

高校数学では、どうしても「問題が解けない（解答にたどりつかない）」という場合が中学の場合と比べて多く発生すると思います。そういう時には、勉強の１つのコツとして、問題の「解答」を先に見てしまってください。

すると、じつは意外に簡単で基本的な基礎事項をいくつか組み合わせるだけの問題であったりします。それを知ったうえで、再度問題を解いたり他の問題にも手をつけてみて、そういったレベルのものであれば確実に解けるように練習を積んでみる事が勧められます。解答を見ても基礎事項の組み合わせで済むとは到底思えない「難問」の場合は、普段の勉強においても後回しにして放置して大丈夫です。
まずは、基礎事項とその組み合わせからなる問題を確実に・正確に・速く解けるようにしましょう。

基礎事項がよく把握できていない場合は、落ち着いて分からない部分について一度基礎事項を整理し、内容の把握に努めましょう。この時、公式や定理だけを見て暗記しようとしない事が中学校の時以上に重要です。例えば三角関数の分野１つだけとってみても非常に多くの「公式」があり、無理に暗記しようとしても中学の時以上に相当厳しいものがあると思います。

暗記しないでどのように覚えるのかと言われるかもしれませんが、例えば三角関数で言えば正弦と余弦の公式を把握していれば正接の公式は計算で出せますし（その関係自体、重要事項です）、
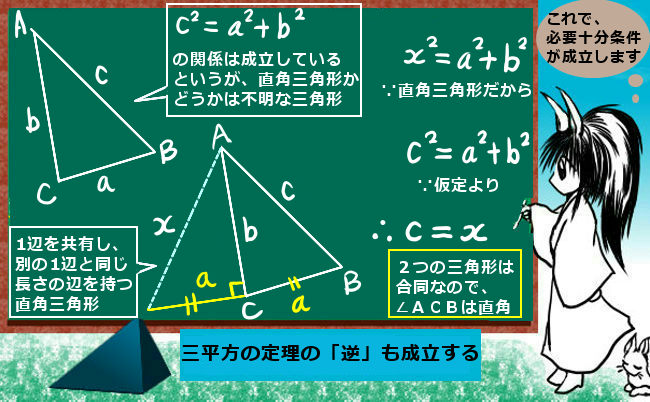
sin２θ＋cos２θ＝１という基本公式は本質的には「三平方の定理」である事を理解していれば「暗記」の負担は相当に減るでしょう。余弦定理の場合、角度が直角である場合は三平方の定理に他ならない事を知っておけば、定理の内容の大半は全く新規のものではなく既に知っているという事になります。
このように、全ての定理や公式を全く別物と捉えるのではなくて、数学的な関連付けをする事で結果的に暗記する項目を減らせるのです。

そういった「整理された基礎事項の知識」を練習問題や入試問題を解く中でアウトプットしていく事を積み重ねていくと、数学の知識は定着し成績は伸びていきやすいかと思います。

高校数学の場合には「基礎」を正確に押さえる段階に至るまでが、中学の時と比べて労力を要するという面があるかもしれません。その事をあらかじめ踏まえて普段の勉強に取り組むと効率よい学習が可能でしょう。

高校数学の学習で特に気を付けるべき点
  • 高校数学では教わる内容の範囲が広い。（それぞれ無関係ではなく関連はある。）
  • 公式や定理の数も多く、相互の分野の関連付けをしないと基礎知識の整理が難しい場合もある。

微積分が出題範囲の時

大学の理系の学部の入試では微積分まで問われる事が多いと思います。

微積分の範囲まで学習する場合には、微分の場合には関数の極大・極小を調べてグラフを描く問題、積分の場合には面積・体積を計算する問題が比較的多く、合成関数や積の微分公式、置換積分・部分積分の公式なども合わせて使う場合もあります。また一部、特定の関数の極限を計算させる出題などもあります。

勉強法としては微積分以外の分野と同じように考えます。

ただし微積分に関しては、まず基本になるのが微分のほうで、その計算に慣れてきたら積分のほうに移れるという性格が強いです。（これは積分は微分の逆演算であるという性質によります。）また三角関数や指数関数の知識など、微積分以外の分野の正確な理解が必要な事も多いです。そのため、それらの理解がまだじゅうぶんでない場合には一度戻ってみる事も有効な手段かもしれません。

まとめと結び

こういった勉強法は、中学や高校だけでなく、資格取得などの時にも有効なものです。まず必要な基礎事項を詳しく整理・把握・理解し【それは「公式」の暗記ではありません】、演習問題・試験の過去問題を使って練習を積むというものです。

数学の成績を伸ばすために勧められる勉強法について以上の事を整理しておきます。

まとめ
  • 数学を勉強する時には、まずは基礎知識を大事にしよう
  • 出題範囲を整理して、勉強不足の分野がないようにしよう
  • 公式や定理を無理に暗記するのは避け、内容の理解に努めよう
  • 基礎知識がある程度理解できたら、その知識が完璧でなくてもいいので練習問題や入試の過去問題を解いてみるようにする。それによって知識が定着する。
  • 理解が不足している場合にはもう一度基礎知識の整理に戻る
  • 出題範囲が広い・公式の数が多いといった時には相互の数学的な関連を理解する等の、何らかの工夫が必要がある場合もある
  • 高校数学でどうしても解答が出せない場合は解答を見てしまうのも１つの手。基礎知識の組み合わせで解ける事も多く、それを知る事自体が勉強になる。それを踏まえて改めて問題を解くようにする。

大学数学の場合は、必ずしも問題を解く事が学ぶ目的ではないのですが、大学によって試験で高得点をとる事・問題を解く事を重視する方針であるというのであれば、やる事は高校までの勉強法と同じです。
（個人的には、問題を解くという事に関しては多くの人が高校までにじゅうぶんやってきていると思うので、大学ではもう少し学問や研究をするという意味での勉強に重点を置いたほうがよいのではないかという気はいたします。）

組み合わせの総数【場合の数】

恭平

組み合わせの総数について説明します。順列と同じく「場合の数」の分野に属する個数の数え方です。これは確率でも使用しますし、２項定理を始めとして種々の計算にも使われる事が特徴です。
（英：組み合わせ【数学の用語として】 selection, combination）

目次：

  1. 考え方・・順番を区別せずに選ぶ
  2. 結論の式と公式
  3. 自然数になる？
  4. 別の方法はある？

考え方・・順番を区別せずに選ぶ

順列が並び方を区別するのに対して、
組み合わせは本当に「何を選んだか」だけを問題にして順番は無視するというものです。

例えば、４つのものを並べる順列の総数は４！通りですが、
４つのものから４つを選ぶ組み合わせは１通りだけです。

順列：｛Ａ，Ｂ，Ｃ，Ｄ｝｛Ａ，Ｂ，Ｄ，Ｃ｝｛Ａ，Ｃ，Ｄ，Ｂ｝｛Ａ，Ｄ，Ｃ，Ｂ｝,・・他　２４通り
組み合わせ：｛Ａ，Ｂ，Ｃ，Ｄ｝の１通り

４つのものから３つを並べる順列の総数は４・３・２＝２４通りですが、組み合わせの場合はどうなるでしょう。具体的に書きだしてみると、｛Ａ，Ｂ，Ｃ｝｛Ａ，Ｂ，Ｄ｝｛Ａ，Ｃ，Ｄ｝｛Ｂ，Ｃ，Ｄ｝の４通りだけという事になります。これを記号では４Ｃ３＝４のように書きます。

尚、４つのものから３つを選ぶという事は実際のところ「残る余りの『１つ』」の選び方と同じなので、ただちに「４通り」と言う事もできます。これは次に触れるように、公式のような形で定式化する事もできます。

「組み合わせ」を考える時には順序を考えません。

「並び方を区別しないのだから組み合わせのほうが簡単か？」というと、「その総数」が組み合わせの場合のほうが少なくなるのは正しいです。
ただし、考え方としては多分順列のほうが簡単で、順列を理解してから組み合わせを考える方が学習の手順としては便利です。

結論の式と公式

公式にすると、結論は次のようになります。

組み合わせの総数を表す式

ｎ個の中からｍ個を選ぶ「組み合わせ」の総数をｎＣｍの記号で表し、次式のように計算できます。$$_nC_m=\frac{_nP_m}{m!}=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m!}=\frac{n!}{(n-m)!m!}$$ここで、等号で結ばれてる部分は式変形しているだけで、どの方法で計算しても良いという事です。ｎＰｍは順番を区別した「順列の総数」を表します。

成り立つ関係式

特に、ｍ＝ｎ、ｍ＝１の場合や、ｎ－ｍ個を選ぶ場合には次式が成立します。$$_nC_n=1\hspace{20pt}_nC_1=n\hspace{20pt}_nC_{n-m}=_nC_m$$

この組み合わせの記号ｎＣｍを２項係数と呼ぶ事もあります。（名称が違うだけで中身は全く同じです。）
その名称の由来は冒頭で触れましたように、２項定理で係数として表される事によります。

考え方としては次のようにします。

まず、ｎ個からｍ個を選び「並び替える」場合はｎＰｍ通りです。この時、「ｎ個からｍ個を選ぶ」という操作はじつはすでにやってしまっているんですね。

ただし順列の場合は、その「選んだｍ個の並び替え」も実行して、総数にカウントしているわけです。言い換えると、順番を区別していない「組み合わせ」のそれぞれを「ｍ個を並び替変えの総数：ｍ！通り」倍しているわけです。

例えば、５つから３つを選んで｛Ａ，Ｃ，Ｄ｝であったとしましょう。これは、順番を区別していないものです。つまり、｛Ｃ，Ａ，Ｄ｝と書いても同じものとします。

ここで、順列の場合は、｛Ａ，Ｃ，Ｄ｝の並び替えもカウントするので、この組み合わせに対して３！＝６通りあるわけです。

これは他の組み合わせ｛Ｂ，Ｃ，Ｅ｝などに対しても並び替えれば３！＝６通り発生するわけで、他の組み合わせも個体の数が同じですから同様に並び替えで３！＝６通りずつ発生します。

結局、次のようになります：
「組み合わせの総数【ｎＣｍ】」×「選ぶ個数【ｍ】に対する順列の総数【ｍ！】」
＝「ｎ個からｍ個選んで並び替える順列の総数【ｎＰｍ】」
という事になります。これを式で書くと次のようになります。

$$(_nC_m)\cdot (m!)=_nP_m\hspace{5pt}\Leftrightarrow \hspace{5pt}_nC_m=\frac{_nP_m}{m!}$$

これが、組み合わせの総数を表す公式の意味です。

この式の続きは、単なる分母と分子の約分の計算になります。順列を階乗だけで表す形にすれば組み合わせの式もｎとｍを使った階乗で表される形になります。

この式を使えば、例えば７個から３つ選ぶ場合の組み合わせの総数は、次のようになります。

$$_7C_3=\frac{7\cdot 6\cdot 5}{3!}=\frac{7\cdot 6\cdot 5}{3\cdot2\cdot1}=35$$

このように「３５通り」という結果が比較的簡単に分かるわけです。尚、これが順列であれば６倍の２１０通りですから、並び替えずに組み合わせにすると大きな数に比較的なりにくい傾向がある事も分かります。

ここで、同じ組み合わせを階乗だけの形で書くと、

$$_7C_3=\frac{7!}{(7-3)!3!}
=\frac{7!}{4!3!}$$

他方、７つから４つ選ぶ組み合わせの総数は、

$$_7C_4=\frac{7!}{(7-4)!4!}
=\frac{7!}{3!4!}$$

であり、これらは同じ数ですね。７個から３つ選ぶ場合も４つ選ぶ場合も、同じく３５通りです。これは、３つ選んだら残り４つも必然的に決まるのだから同じ総数になって当然であると考えてもよいですし、一般のｎとｍに対する式変形で示す事も可能です。

式で示す場合、ｎ個から（ｎ－ｍ）個を選ぶ組み合わせの式を作ってみればよいのです。

$$_nC_{n-m}=\frac{n!}{\{n-(n-m)\}!(n-m)!}=\frac{n!}{m!(n-m)!}= _nC_m$$

分母のところの掛け算が順番を入れ替えても同じになる事から、この関係が成り立ちます。つまり、７個から２個選ぶ組み合わせの総数が分かったら、７個から５個選ぶ組み合わせの総数も同じであるので計算不要という事です。（順列の場合は、そのようにする事はできません。）

必ず自然数になる？

さてここで、言われると確かにそのように納得できるかもしれないが、順列の総数を「ｍ！」で割る時に「自然数になる」保証はあるのか？と思うかもしれません。

これは「理解」する方法としては、「組み合わせの総数が１.５通りとか２／３通りになる事はあり得ないので、必ず自然数であるに決まっている」・・と、捉えても支障はありません。
実際、どうやっても自然数にしかならないからです。

他方で、順列とか組み合わせとかを離れて、単に自然数ｎとｍを持ってきて次式が自然数になるか否かという問題が提示された時に「組み合わせだから自然数」と言うのは数学的な証明には、もちろんなりません。

次の式は必ず自然数になる？

ｎ、ｍを自然数（ｎ≧ｍ）として $$\frac{n!}{(n-m)!m!}=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m!}$$ （これが「組み合わせの総数」を表す前提はないものとして）

結論は、この式は必ず自然数になります。分子は分母で必ず割り切れて余りはでないという事です。

そのようになる事に対する一番簡単な証明は、「順番にｎ個並んだ自然数の中には、ｎの倍数が少なくとも１つ必ず含まれている」という事を根拠にするものです。

例えば、順番ずつ３つ並んだ自然数の中には、３の倍数が少なくとも必ず含まれています。これは、どんなでたらめな自然数を持ってきても、それに＋１、＋２する形（あるいは－１、－２）する形で並べてあげると３の倍数が必ず含まれるという事です。

２１４というてきとうな自然数をもってきて、｛２１４、２１５、２１６｝と並べれば、この場合は真ん中の数が３の倍数ですね。この理屈の意味自体は簡単で、１,２,３,４,５,６,７,８,９,・・・と、並べたとき、どこでもいいから数が３つ含まれるように区切ると、どうやっても３の倍数は１個以上含まれるという事です。

３でなくても、５でも６でも７でも、任意の自然数でそのようになります。
もう少し一般的に言うと、例えば３の倍数なら、任意の自然数は３ｎ, ３ｎ＋１, ３ｎ＋２ のいずれかで表されるので１を加えていくか引いていく形で３個並べれば、その必ず３ｎの形のものが存在するという事です。

$$_nC_m=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m!}$$

の形で見るのが一番分かりやすいかと思いますが、式の分子の（積の）項数はｍ個です。他方、分母はｍ！＝ｍ(ｍ－１)(ｍ－２)・・・３・２・１ですから、ｍ以下の自然数しか含まれません。そのため、分子に含まれる任意の自然数の倍数は、必ず分母に存在するという事です。これが基本的な考え方です。

話が少しややこしくなるのは、組み合わせの式の場合では分子に複数の自然数があるためです。仮に自然数ｐとｑの倍数が共通する数として分母に含まれていたら、必ず割り切って全体として自然数になるかが怪しくなる可能性もあるとも言えるわけです。

しかし実際はそのような事は起きないので大丈夫であるというのが結論です。

まずｎは固定したうえで、ｍまでは確かに割り切れて全体が自然数になるとしましょう。

次のｍ＋１が素数であったら、ｍまでの数のいずれでもないし倍数でもないので、分子のｍ＋１個の中にｍ＋１の倍数が存在し、割り切れる事になります。

ｍ＋１が素数でない場合で、ｍ以下の自然数ｐの倍数になっている時であっても、例えばｐｑ個の中には、ｐの倍数が少なくとも「ｑ個」含まれています。これは、ｐ個の塊で区切れるところがｑ個あるためです。
そのうえで、ｐｑの倍数も１個以上あるので、分母の１つのｐの倍数を既に割って使ってしまったあとでも別のｐの倍数が必ず残っています。それで、ｍ＋１＝ｐｑの倍数も分母に必ずあるので、再び全体として割り切って自然数になるというわけです。

具体例では、８Ｃ３＝８・７・６／(３・２・１) は確かに自然数になりますが、続いて８Ｃ４を考えた時に、８Ｃ４＝８・７・６・５／(４・３・２・１)の分母に新たに入った４＝２２について、すでに分母にある２については、分母の項数が４つなので、２の倍数は２個以上あります。（この場合、見れば分かる通り６と８です。）分母の４項の中で、４の倍数は必ず１個以上ある事は確定しています。

Ａ，Ｂ，Ｃ，Ｄと並べたところの１つが４の倍数だと考えると分かりやすいかと思いますが、例えばＢの位置にあったとき、Ｃ、Ｄは使用しませんが、２の倍数は２個ずつ区切ったＡ，ＢとＣ，Ｄのどちらにも１個ずつ含まれます。このようにして、分母にすでに２がある事で４で割り切れなくなってしまう心配はないという事です。

４つの続く自然数には２の倍数と４の倍数がどちらも必ず含まれ、同様に８つの続く自然数には２の倍数、４の倍数、８の倍数がそれぞれ必ず含まれます。
９個の続く自然数には３の倍数と９の倍数がどちらも必ず含まれます。

少しややこしい理屈である事は間違いありませんが、基本的な考え方は一般のｎとｍに対しても同じ事です。

このようにして、組み合わせの総数を表す式はきちんと「割り切れて」自然数になる事が式の形からも保証されます。

別の方法はある？

「組み合わせを順列を使って表せるのは分かったが、別の方法はないのか」

あります。場合の数を考える時には考え方は１つとは限らず、複数の考え方で同じ結論になる事はよくあります。ただし、組み合わせに関して言えば順列を階乗で割る表し方が一番簡単ではないかと思います。

別のやり方としては、１つの例として次のように組み合わせを考える事もできます。

Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆ，Ｇの７つから４つ選ぶ場合、まず「Ａを含む場合」、残り３つを６つから選びます。次に、Ａを含まずＢを含む場合、Ａ，Ｂを含まない５つから３つを選びます。
こういう具合に考えても組み合わせの総数を表す事ができて、次の関係が成立します。

$$_nC_m=_{n-1}C_{m-1}+_{n-2}C_{m-1}+_{n-3}C_{m-1}+\cdots +_{m}C_{m-1}+_{m-1}C_{m-1}$$

６つから３つを選ぶ組み合わせは、さらに５つから２つを選ぶ場合・４つから２つを選ぶ場合・・に分割できます。数が少なくなれば「明らかに」分かる組み合わせの場合にたどり着きます。
７つから４つ選ぶ時に実際にこれが正しいのかを見てみると、

$$_7C_4=_{6}C_{3}+_{5}C_{3}+_{4}C_{3}+_{3}C_{3}=20+10+4+1=35$$

通常の組み合わせの公式で計算すると、

$$_7C_4=\frac{7\cdot 6\cdot 5\cdot 4}{4\cdot 3 \cdot 2 \cdot 1}=35$$

この通り一致するわけですが、これは次の理由になります。
まず分母の７を（４＋３）の形に書きます。

$$_7C_4=\frac{(4+3)\cdot 6\cdot 5\cdot 4}{4!}=\frac{4\cdot 6\cdot 5\cdot 4+3\cdot 6\cdot 5\cdot 4}{4!}=\frac{6\cdot 5\cdot 4}{3!}+\frac{3\cdot 6\cdot 5\cdot 4}{4!}$$

$$=_6C_3+\frac{3\cdot (4+2)\cdot 5\cdot 4}{4!}=_6C_3+\frac{4\cdot 5\cdot 4\cdot 3+2\cdot 5\cdot 4\cdot 3}{4!}=_6C_3+_5C_3+\frac{2\cdot 5\cdot 4\cdot 3}{4!}$$

$$=_6C_3+_5C_3+\frac{2\cdot (4+1)\cdot 4\cdot 3}{4!}=_6C_3+_5C_3+_4C_3+\frac{ 3\cdot 2\cdot 1}{3!}=_6C_3+_5C_3+_4C_3+_3C_3$$

一般のｎとｍの場合も同じで、分母の一番大きい項を(ｍ＋ｐ)の形にして分離していくとこの形になります。

しかし言い換えると、この考え方でやったとしても結果は同じでnCm＝(nＰm)／(ｍ！) と同じ式になるのです。

順列とは？

恭平

順列とは、Ｎ個のものを並び替える方法を言います。
（英：permutation　順列を「置換」とも言います。）ここでは、その方法が何通りあるかという「場合の数」について説明します。高校数学で扱うのはその事項です。

結論を先に言うと、Ｎ個のものを並び替える順列の総数は次式で表されます。

Ｎ個のものを並び替える順列の総数

$$_NP_N=N!$$ $$=N(N-1)(N-2)\cdots 3\cdot 2\cdot 1$$ ＮＰＮという表記は、Ｎ個のうちＮ個全てを並び替えるという意味です。
びっくりマークは「階乗」を表します。自然数を１ずつ下げてＮから１まで掛けて積の形にする事を指します。例えば５！＝５・４・３・２・１＝１２０です。

また、Ｎ個のもののうち、Ｍ個を並び替え方の総数は次の通りです。

Ｎ個のもののうちＭ個を並び替える順列の総数 $$_NP_M=\frac{N!}{(N-M)!}$$

このようになるわけですが、これらを「暗記」するのはやめましょう。確かに公式の中には暗記してしまったほうが早いものもありますが、この順列の総数に関する式は「理解」できるものです。

Ｎ個のものを並び替える方法

初めに、少ない数から具体的に見てみましょう。

２個のものがあったとき、これを並び替える方法は「２通り」です。{Ａ,Ｂ} {Ｂ,Ａ} の２通りです。他の文字・・例えば {甲,乙}{乙,甲}の２通りと考えても、何でも構いません。
要するに、順番を区別して数えるという事なのです。
これが「２つのものを並び替える順列の総数」２Ｐ２＝２の意味です。この場合はとても簡単ですね。

では、Ａ，Ｂ、Ｃあるいは甲、乙、丙などの３つを並び替えるにはどうすればよいでしょう？

これを具体的に書くと、
｛丙、乙、甲｝｛丙、甲、乙｝｛乙、丙、甲｝｛乙、甲、丙｝｛甲、丙、乙｝｛甲、乙、丙｝
の６通りあります。

実際これしか順番に並べる方法はないのですが、どのようにしてこれらを書きだしたかを説明します。まず、最初に来る文字が甲、乙、丙の３人のパターンがあります。そしてそれぞれの場合について、続く２人の順番が２通りあります。丙を一番左に置いたとき、続く順番は｛乙,甲｝と｛甲,乙｝の２パターンであるという事です。そして次に乙が最初に来る場合を考えて、同様に書きだして上記の６パターンの並びを得ています。

つまり３人それぞれを特定の場所、例えば一番左に置く場合につき２通りあるので３×２＝６通りの並び替えの方法があるというわけです。これが３Ｐ３＝３！＝６の意味です。

では４人を並び替える場合はどうするかというと、１つの位置（例えば一番左）に誰かをおくと、そのパターンにつき「３人を並び替える方法がある」事に気付くと分かりやすいかと思います。

誰かが一番左にいるごとに残りの３人を並べる方法が６通りあります。一番左に誰が来るかについては全部で４人いるわけですから４通りになります。よって４人を並び替える方法は全部で４×６＝２４通りです。

ここで、３人を並び替える方法が３×２＝６通りであった事を考えると、４人を並び替える方法は４×３×２＝２４通りであるとも言えます。これが４Ｐ４＝４！＝２４の意味です。

では５人になった場合はどうかというと、考え方は同じです。

まず５人のそれぞれをどこか固定した位置に置きます。例えば上の例と同じく一番左に置きます。すると、残りの４人の並び替えは２４通り（４！＝４×３×２通り）である事が分かっているので、５人のそれぞれに対して２４通りですから５×２４＝１２０通りの並び替えの方法があります。これをまとめて５！通りと書く事もできて、これが５Ｐ５＝５！＝１２０の意味です。わずか５人で、並び替えの方法は意外に多いという事が分かります。

６人の場合も同じで、６×５！＝６×１２０＝７２０通りになります。これもこれまでと同様に６！＝７２０通りとも書けます。非常に数が増えて、１つ１つ手で紙に具体的に書きだすのは困難である事が分かります。

７人の場合は７！＝７×６！＝７×７２０＝５０４０通りになります。以降、人数を増やしていくと並べ方の総数は莫大に増えていく一方です。

以下、何人いても考え方は同じで、Ｎ人いた場合にはまずＮ人を選びます。のこりＮ－１人についてみるとこれは（Ｎ－１）×「Ｎ－２人の場合」ですから、結局Ｎ×（Ｎ－１）×（Ｎ－２）×・・・×３×２＝Ｎ！通りという事になるわけです。
【ＮＰＮ＝Ｎ×Ｎ－１ＰＮ－１＝Ｎ×(Ｎ－１)！＝Ｎ！のようにも書けます。考え方はある程度自由です。】

これが「Ｎ個のものを並び替える順列の総数は ＮＰＮ＝Ｎ！である」という事の意味です。

Ｎ個のうちＭ個を並び替える場合

次に、Ｎ個のものの中からＭ個選んで並び替える方法の総数についてです。
これは順列の記号ではＮＰＭと書きます。

公式だけ見ると一見わけがわからない式に見えるかもしれませんが、意味はじつに簡単です。

５人いて、３人を選んで並び替える方法を考えてみましょう。

５人全員を並び替える場合には５！＝５×４×３×２通りであったわけですが、意味を考えると３人だけを選ぶ場合には、最後の「２倍」がいらないわけです。誰か３人が並んだ時点で、選ばなかった２人も確定しますからそれで終了というわけです。

結果的には話は単純で、最初に５人のうちの１人を選び、次に残った４人の中から１人、続いて残った３人の中から１人を選びそこで打ち切るという事です。
【この方法でＮ個全てを並び替える場合を理解しても支障ありません。】

式で書くと５Ｐ３＝５×４×３＝６０という事です。

５人中２人だけを選び並び替えるなら５Ｐ２＝５×４＝２０通り、５人中１人だけなら５Ｐ１＝５通りです。

この通り、考え方は単純なのですが一般のＮに対して式を書くと多少煩雑になる面があります。

Ｎ個のうち３個を並び替えるという場合にはＮ(Ｎ－１)(Ｎ－２)通りなどと上から順に３項の積を考えて済みますが、Ｎ個のうちＭ個を並び替える場合にはどう書くのかという話になります。

ＮＰ３＝Ｎ(Ｎ－１)(Ｎ－２)の場合を見てみると、Ｎ－３以降の項がないわけですから、Ｎ！を(Ｎ－３)！で割るとちょうどうまい具合に同じ数になります。

つまり、(Ｎ－Ｍ)！を考えて、それでＮ！を割ればうまく式でも表現できるわけです。これがＮＰＭを表す公式の意味です。

$$_N\mathrm{P}_M=\frac{N!}{(N-M)!}$$

尚、Ｍ＝Ｎ－１を考えると、Ｎ－Ｍ＝Ｎ－(Ｎ－１)＝１ですから、それでＮ！を割ってもＮ！のままです。ＮＰＮ－１＝ＮＰＮという事になります。これは５人全員を並び替える時、最後の一人については空いている位置に入れるだけなので結局「５人中４人を選んで並び替える」場合と同じである事に対応しています。

順列の考え方は、具体的な人や物の並べ方を考える時だけでなく、種々の理論の中でＮ個の項を並び替える何らかの操作をする時にその総数を表すために使用されます。

例えば（高校数学の範囲外ですが）線型代数で行列式の定義をする時にはＮ個の項の積をとって並び替えたものを全て考えるという事をやるので、項数は順列の総数という事になります。（Ｎ！という形が出てくる式全てが順列に関係するとは限りません。例えば、単項式に対する微分操作を繰り返す事でＮ！が出てくるパターンもあります。）

また、順列の他に重要な「組み合わせ」の数え方も順列での考え方を基礎としています。方法の総数を数え上げる事は、確率の理論でも重要です。

行列式の項数を表すｎ！はｎ個の番号を並び替える順列の総数です。

逆関数の微分公式【計算例と証明】

恭平

逆関数の微分公式の内容、具体例、証明について述べます。

目次：

  1. 公式の内容
  2. 具体例と計算例
  3. 公式の証明

y = 2x のとき、両辺を２で割って x = y / 2 とも書けます。
このように、y = ｙ(x) のとき、逆に x = ｘ(y) と書けるとき、ｘ(y) を ｙ(x) の逆関数と呼びます。
【この時の関数の記号はｆでもＦでも何であっても問題ありません。】

高校数学の中で重要な例としては、指数関数と対数関数を挙げる事ができます。
これらは、互いに逆関数同士の関係にあるのです。

y=x2 のような場合に逆関数を考えると x=\(\pm \sqrt{y}\)のように x を y で表した関数が２つ出てきてしまうので、「１つの変数に対して１つの値が定まる」という関数の定義に反し、ちょっとした面倒事が起きます。
こういう場合には x の定義域と y の値域を特定の区間に定めれば逆関数を書けるという形になります。
逆関数の定義に関するそういった細かい事は多くあるのですが、ここでは本質ではないので略します。

高校数学で覚える必要はありませんが三角関数の逆関数を「逆三角関数」と言い、
sin x に対して arcsin x（「アークサイン x」）と書きます。
この逆三角関数は一見使いづらい関数なのですが、
その微分の性質から、一部の微積分の計算（例えばテイラー展開や不定積分の計算）で有用な働きをする事があります。この逆三角関数を微分する時には、逆関数の微分公式を使用します。

公式の内容

逆関数を考えた時、もとの関数を微分して得られる導関数と、逆関数を微分して得られる導関数の間にはある関係式が必ず成立するというのが、逆関数の微分公式です。内容は、次のようになります。

逆関数の微分公式

ｙ＝ｙ(x)の時にｘ＝ｘ(ｙ)と表せる時、次の関係式が成立します。 $$\frac{dy}{dx}={\large\frac{1}{\frac{dx}{dy}}}$$ ここで左辺はｘの関数で、具体的な計算においては右辺はｙの関数ですが、ｙはｘで表せるという前提なので右辺もｘだけの関数として表す事ができます。（※ただし後述するように具体的な計算ではｙをｘに直す作業が面倒である事があります。）
もちろん、分母は０になってはいけないという前提はあります。

ちょっと一見よく分からない公式だと思うかもしれませんが、ｘをｙで表した時に「ｘをｙで微分して得られる導関数」の逆数が、もとのｙをｘで微分して得られる導関数に必ず等しくなるという関係式です。

式としては単純で互いに逆数であるという関係ですから、ｄｘ／ｄｙ＝・・の形として見ても公式は成立します。つまり基本的には公式を次のように書き換える事もできます。

$$\frac{dx}{dy}={\large\frac{1}{\frac{dy}{dx}}}$$

これは、具体例で見たほうが分かりやすいと思います。

逆関数
このような逆関数の導関数を考える時、もとの関数の導関数との間に常に成り立つ関係式があります。

具体例と計算例

具体的に公式を使うための手順は次のようになります。
もとの関数ｙ＝ｙ(ｘ)の導関数を計算したい場合であるとします。

  1. 関数と逆関数を、y=y(x),　x=x(y) の形で出しておく。
  2. 逆関数のほうについて、導関数を計算する。【※これが簡単にできる場合でないと、公式を使う意味があまりない事になります。】$$\frac{dx}{dy}を計算$$
  3. 得られた逆関数の導関数（ｙの関数）を、逆関数の微分公式に代入します。$$\frac{dy}{dx}={\large \frac{1}{\frac{dx}{dy}}}\hspace{5pt}に\hspace{5pt}\frac{dx}{dy}\hspace{5pt}を入れる$$
  4. この段階で得られる計算結果は「y の関数」の形になっているので、y=y(x)を代入して x の関数にすれば、
    それが y に対して x で微分したｄｙ／ｄｘの正しい形になっています。 $$式の変数をｘだけにすれば\hspace{5pt}\frac{dy}{dx}\hspace{5pt}の結果になる$$
微分公式
指数関数と対数関数の微分は逆関数の微分公式で結ぶ事ができます。

※合成関数でもこの「y を x の関数の形に戻す」作業がありますが、一般には y = f(x) を代入すればよいというものでした。しかし、逆関数の微分の場合は、この作業について少し工夫がいる場合があります。

具体的な計算例を次に記します。
ここでは参考までに、逆三角関数の微分の計算も記してあります【高校では不要】。

逆関数の微分の具体例

逆関数の微分公式は、通常の微分計算で多く使うというよりは、特定の微分公式を導出するために使われる事が多いように思います。

  • １次関数の例：y＝２,　x＝y／２ の時、 $$\frac{dx}{dy}=\frac{1}{2}\hspace{5pt}により、$$ $$\frac{dy}{dx}={\large\frac{1}{\frac{dx}{dy}}}={\large\frac{1}{\frac{1}{2}}}=2$$ この場合には直接微分しても、あるいはグラフを見ても分かる結果ではありますが、逆関数の微分公式も確かに成立しているという事です。
  • ２次関数の例：ｘ＞０かつ ｙ＝\(\sqrt{x}\), ｘ＝ｙ2 の時、 $$\frac{dx}{dy}=2y\hspace{5pt}により、$$ $$\frac{dy}{dx}={\large\frac{1}{\frac{dx}{dy}}}= \frac{1}{2y} =\frac{1}{2\sqrt{x}}$$ ここでは平方根のほうの導関数を計算するために、２次関数を逆関数とみなしています。
    もちろん、この計算はｙを直接ｘで微分しても同じ結果です。
  • 指数関数と対数関数の例：y＝ex, x＝ln y の時、 $$\frac{d}{dx}e^x={\large\frac{1}{\frac{d}{dy}\ln y}}={\large\frac{1}{\frac{1}{y}}}=y=e^x$$ 指数関数と対数関数の微分公式は一見全く異なる形であるようにも見えますが、じつはこうしたつながりもあるというわけです。
  • 逆三角関数と三角関数の例：ｙ＝ arcsin x, ｘ＝ sin y の時、$$\frac{d}{dx}\arcsin x={\large\frac{1}{\frac{d}{dy}\sin y}}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-\sin^2y}}=\frac{1}{\sqrt{1-x^2}}$$ ここでは「逆三角関数の導関数」を知るために、通常の三角関数を逆関数とみなしています。
    計算過程では sin2x+cos2x=1 の関係を使用しています。
  • 余弦の逆三角関数の例：y＝arccos x, x＝cos y の時、$$\frac{d}{dx}\arccos x={\large\frac{1}{\frac{d}{dy}\cos y}}=\frac{1}{-\sin y}=\frac{-1}{\sqrt{1-\cos^2y}}=\frac{-1}{\sqrt{1-x^2}}$$
  • 正接の逆三角関数の例：y＝arctan x, x＝tan y の時、 $$\frac{d}{dy}\tan y==\frac{1}{\LARGE{\frac{1}{\cos^2y}}}\hspace{5pt}により、$$ $$\frac{d}{dx}\arctan x={\large\frac{1}{\frac{d}{dy}\tan y}}=\cos^2y=\frac{1}{1+\tan^2y}=\frac{1}{1+x^2}$$

高校数学では、指数関数と対数関数の関係あたりを逆関数の関係で結べる事を理解していれば、基本的にはじゅうぶんかと思います。

逆三角関数の微分
【逆関数の微分公式：arcsin x の導関数の導出の例：】arcsin xの微分を、「sin xの微分公式」と「逆関数の微分公式」から導出する手順です。x = sin y の時に「y を変数とする形」で逆関数の微分を出すのは、じつはかなり簡単です。（公式により y で微分し分母に入れるのみ。）
ただ、そのあとで y を x の関数の形にうまく戻すために、工夫が必要な事があるのです。
※逆三角関数の別の表記方法

あくまで表記方法の問題なのですが、逆三角関数を sin-1xとも書きます。
もちろんその場合は(sin x)-1=１／(sin x) とは全く異なる関数・・なのです。
個人的にこれは紛らわしい表記だとも思うので、このサイトでは arcsin x などの表記を使用します。

公式の証明

y=Y(x), x=X(y) として、まず Δｘ = X(y+k)－X(y) とすると
k → 0 の時に Δx → 0 となります。（その逆である「Δｘ→ 0 の時 k → 0 」も成立）

X(y+k)－X(y) について Δx という文字でおいたのは、ここでは X(y+k)－X(y) というものが「ｘの変化」に等しいという事を見やすくするためです。別に他の文字でも支障はありません。

これを上手に利用すると、同じ極限が２通りの方法で表せます。その２通りの方法による結果がｄｙ／ｄｘと１／（ｄｘ／ｄｙ）であり、それゆえに両者を等号で結べるというのが証明の内容です。
その点で、合成関数の微分公式のように１本の式だけで証明できない点が少しだけ異なります。

ここで、微分の定義の式を書きます。

$$\frac{dy}{dx}={\large\lim_{\Delta x \to 0}\frac{Y(x+\Delta x)-Y(x)}{\Delta x}}$$
これは定義通りの式です。しかし、極限をとる変数としてΔｘを使っているところに計算上の工夫があります。ここの極限をとる変数は、h でなくとも何でも成立します。

上記の微分を表す微分を計算すると、次のようにも表せます。

$$ {\large\lim_{\Delta x \to 0}\frac{Y(x+\Delta x)-Y(x)}{\Delta x} } =\lim_{k \to 0}{\large\frac{Y(X(y)+X(y+k)-X(y))-Y(X(y))}{\Delta x}}$$
$$ ={\large\lim_{k \to 0}\frac{Y(X(y+k))-Y(X(y))} {\Delta x}} ={\large\lim_{k \to 0}{\large\frac{y+k-y}{\Delta x} }} ={\large\lim_{k \to 0}\frac{k}{\Delta x} }={\large\lim_{k \to 0}\frac{1}{\frac{\Delta x}{k}} }$$
$$ ={\large\lim_{k \to 0}\frac{1}{\frac{X(y+k)-X(y)}{k}} } ={\Large\frac{1} {\frac{dX(y)}{dy}}}={\Large\frac{1}{\frac{dx}{dy}} }$$

最初の変形では、分子のところだけΔｘをもとの形Δx = X(y+k)-X(y)に直してしまい、
ｘをｘ＝Ｘ(y)で書く事により、ｘ＋Δｘ＝X(y+k)としています。

次に、関数を y 変数になるように整理し、Δx→0 の時 k→0 なので k の極限にしています。

そのあとで、少しややこしいのですが逆関数の重要な性質「Ｙ(Ｘ(y))＝Ｙ(x)＝y 」（Ｘ(y)＝ｘに注意）を使って、Ｘ(Ｙ(y+k)) = y + k としています。
その後の計算は、例えば２／３＝１÷（３／２）＝１／（３／２）などと、同じ計算です。

これらの結果から、
$$\lim_{\Delta x \to 0}{\large\frac{Y(x+\Delta x)-Y(x)}{\Delta x}}=\frac{dy}{dx}={\Large\frac{1}{\frac{dx}{dy}} }【証明終り】$$

逆関数の性質
Ｘ(ｙ)＝ｘ に y＝Ｙ(ｘ) を代入して Ｘ(Ｙ(ｘ))＝ｘ としても同じです。
サイト内関連記事【高校数学の微積分】

積の微分公式と商の微分公式

恭平

積の微分公式と、それの変形版である商の微分公式の内容、具体例、証明について述べます。
（英：product rule, quotient rule）
これは関数同士の「掛け算」「割り算」の形になっている関数を微分する時に成立する公式です。

目次：

  1. 公式の内容
  2. 計算の具体例
  3. 公式の証明

積と商の形の関数は統一的に捉える事ができるので同時に記します。
詳しくは後述していますが、商の場合にはｆ(ｘ)と１／ｇ(ｘ)の「積」と捉えればよいので基本的には同じ形の公式なのです。

公式の内容

ｙ＝ｘｅｘ といった関数同士の「積」の形になったものを微分する時には積の微分公式が使えます。
また、正弦関数を「x で割った」(sin x)／x などには商の微分公式が使えます。

関数ｆ(ｘ)とｇ(ｘ)の積ｆ(ｘ)ｇ(ｘ)、商ｆ(ｘ)／ｇ(ｘ)　を微分した時には次の公式が成立します。
ここで、ｆ(ｘ)とｇ(ｘ)をｆ、ｇと記しています。

積と商の微分公式

$$積の微分公式：(fg)^{\prime}=f^{\prime}g+fg^{\prime} \hspace{20pt}商の積分公式\left(\frac{f}{g}\right)^{\prime}=\frac{f^{\prime}g-fg^{\prime}}{g^2}$$ これらは本質的には全く異なる公式ではなく、同種類のものであると捉えたほうがよいでしょう。

商の微分については、分母にあるのは「『微分してない g(x)』の２乗」です。

積の微分公式については、２つの項は足し算なので順番はどっちでもよいのですが、
「ｆ’ｇ +ｆｇ’」の順番にしたほうが、商の微分公式との関係で「覚えやすい」かとは思います。

計算の具体例

公式を使って計算する手順としては、f(x) と g(x) のそれぞれについて「x で微分した関数」と、「微分してない（もともとの）関数」をパーツとして用意し、公式に当てはめて丁寧に計算するというものになります。

まず、積の微分公式の具体的な計算の例をいくつか見てみます。

積の微分公式を使った計算例
  • ｙ＝sinx cosx 【２つの三角関数の積】の微分は次のようになります。$$\frac{d}{dx}\{(\sin x)(\cos x)\} =(\sin x)^{\prime}(\cos x)+(\sin x)(\cos x)^{\prime} =\cos^2x-\sin^2x$$
    加法定理を考えると、この結果はcos 2x に等しくなります。sin x cos x=(sin 2x)／2 として、ｘで微分した時の結果と一致します。（この時、合成関数の微分公式を使用しているので注意。）
  • ｙ＝sin２x の微分を考えます。
    これに積の微分公式を適用する場合にはｙ＝(sin x)・(sin x)と考えるわけです。$$\frac{d}{dx}\{(\sin x)(\sin x)\} =(\sin x)^{\prime}(\sin x)+(\sin x)(\sin x)^{\prime} =2\cos x\sin x$$
    これは sin 2x と表す事もできます。
    また、sin2x を合成関数の微分公式で微分した結果と一致します。
    さらに、加法定理・半角の公式でsin２x＝（１－cos２ｘ）／２と変形してからｘで微分しても同じ結果です。
  • ｙ＝ｘeｘ【ｘと指数関数の積、ｅは自然対数の底】を微分すると次のようになります。 $$\frac{d}{dx}(xe^x)=(x)^{\prime}e^x+x(e^x)^{\prime}=e^x+xe^x=e^x(1+x)$$ 微分公式 (eｘ)’ ＝ eｘ を使っています。
  • ｙ＝ｘlnｘ【ｘと、ｅを底とする対数関数の積】の微分を考えます。 $$\frac{d}{dx}x\ln x=(x)^{\prime}\ln x + x(\ln x)^{\prime}=1\cdot \ln x + x\cdot \frac{1}{x}= \ln x + 1$$ これを変形して両辺を積分すると、対数関数についての積分のほうの公式が得られます。$$\ln x = \left(\frac{d}{dx}x\ln x \right) – 1 なので、$$ $$\int \ln x dx=x\ln x -x+C が得られます。$$
  • 積分のほうの「部分積分」の公式は、積の微分公式を変形して
    $$f^{\prime}g=(fg)^{\prime}-fg^{\prime}$$の両辺を積分したものです。
  • ｆ(ｘ)・{g(ｘ)}－１を、合成関数の微分公式も使って積の微分公式に適用すると商の微分公式が得られます。これについてはこのページで後述する証明の箇所でより詳しく説明します。

２番目の例のように微分の計算方法がいくつかあって、積の微分公式を使う事はその方法の１つであるというパターンもあります。計算結果が合っていればどの方法でも構いません。（入試を受験する場合にはなるべく効率のよい計算方法を考えたり、複数の方法で微分する事で計算結果のチェックをするようにしたほうがいいと思います。）

これらの中で、具体的な関数の微分計算も大事である場合もあるのですが、特に積分のほうの部分積分の公式を得るために使われるという事は覚えておくと便利かもしれません。

続いて、商の微分公式の具体的な計算例です。

商の微分公式を使った計算例
  • ｙ＝(sin ｘ)／ｘ を微分すると次のようになります。 $${\large\frac{d}{dx}\frac{\sin x}{x} =\frac{ (\sin x)^{\prime}x-(x)^{\prime}(\sin x) }{x^2} =\frac{x\cos x-\sin x}{x^2} }$$
  • ｙ＝(ln ｘ)／ｘ を微分すると次のようになります。 $${\large\frac{d}{dx}\frac{\ln x}{x} =\frac{(\ln x)^{\prime}x-(x)^{\prime}\ln x}{x^2} =\frac{x\frac{1}{x}-\ln x}{x^2}=\frac{1-\ln x}{x^2} }$$
  • 正接関数 tan x の微分公式は、じつは商の微分公式により導出されます。$$\tan x=\frac{\sin x}{\cos x}なので、$$ $$\frac{d}{dx}\tan x=\frac{(\sin x)^{\prime}(\cos x)-(\sin x)(\cos x)^{\prime}}{\cos^2x}=\frac{\cos^2x +\sin^2x}{\cos^2x}=\frac{1}{\cos^2x} $$sin x と cos x の微分公式を用いて丁寧に計算すれば証明できます。
    三角比の公式 sin２ｘ＋cos２ｘ＝１を使用しています。
  • 三角関数のマイナー組である余接 (cos x)／(sin x)、正割 1／(cos x)、余割 1／(sin x) 【高校ではこれらを覚える必要なし】の微分公式も、商の微分公式を用いれば証明できます。
    具体的な計算例として、余接関数を微分すると次のようになります。$$\frac{d}{dx}\cot x=\frac{d}{dx}\frac{\cos x}{\sin x}=\frac{(\cos x)^{\prime}\sin x-\cos x(\sin x)^{\prime}}{\sin^2x}=\frac{\sin^2 x+\cos^2 x}{\sin^2x}=\frac{1}{\sin^2x}$$
    正割のように 1／g(x) の形の場合、f(x) = 1 ですから、f'(x) = 0 であり、公式の項が１つ消えるので計算は簡単になります。
    一般的に、 1／g(x) の形の関数の微分は次のようになります。 $$\left(\frac{1}{g}\right)^{\prime}=\frac{0\cdot g-1\cdot g^{\prime}}{g^2}=\frac{g^{\prime}}{g^2}$$これは公式として新たに暗記する必要はありません。
    むしろ、商の微分公式でこのような式もすぐに導出できるようにしておくとよいでしょう。

これらの具体例を見てみると積と商の微分公式は、初等関数の微積分という範囲に限って見ると割と重要な公式である事が、何となくつかめるのではないかと思います。

公式の証明

証明の方法は合成関数の微分公式や逆関数の証明方法と大体考え方は似ています。積や商の微分公式の場合、証明は合成関数や逆関数と比較すると比較的容易です。

結論を言うと「隠れている『０』」を加えたりしてあげる事で証明できます。

■ 積の微分公式の証明　■ 商の微分公式の証明
■ 片方の公式からもう片方の公式を導出するやり方

積の微分公式の証明

積の微分公式の場合、 f(x+h)g(x) － f(x+h)g(x) という「隠れている項」を考える事で、２つの導関数の和の形を作れます。 この考え方自体は、数学の他のところ（大学数学も含め）でも、割とよく使われます。

$$\frac{d}{dx}(f(x)g(x))={\large \lim_{h \to 0}\frac{f(x+h)g(x+h)-f(x)g(x)}{h}}$$
$$={\large\lim_{h \to 0}\frac{f(x+h)g(x+h)-f(x+h)g(x)+f(x+h)g(x)-f(x)g(x)}{h} }$$
$$ ={\large\lim_{h \to 0}f(x+h)\frac{g(x+h)-g(x)}{h} }+\lim_{h \to 0}g(x){\large\frac{f(x+h)-f(x)g(x)}{h} }$$
$$ =f(x){\large\frac{dg}{dx} }+g(x){\large\frac{df}{dx}}=f(x)g^{\prime}(x)+f^{\prime}(x)g(x) =f^{\prime}g+fg^{\prime}【証明終り】$$


証明の最後のところは、f(x)をf と略して和の順番を変えて整理しただけになります。

「隠れている『０』」の項を分子の部分に加えてあげる事で証明できます。積の微分公式の場合、
f(x+h)g(x) － f(x+h)g(x) ＝０という項を加える事で「２つの導関数の和」の形を必ず作る事が可能です。

商の微分公式の証明

商の微分公式も同様の方法で証明できます。

まず分母のg(x+h)とg(x)を通分します。
その後で「-f(x)g(x)+f(x)g(x) (=0)」を分子に加えるという、積の微分公式同様の考え方をします。

$$\frac{d}{dx}\frac{f(x)}{g(x)}={\large\lim_{h \to 0}\left(\frac{f(x+h)}{g(x+h)}-\frac{f(x)}{g(x)}\right)\cdot\frac{1}{h}}$$

$$={\large\lim_{h \to 0}\frac{f(x+h)g(x)-f(x)g(x+h)}{h\cdot g(x)g(x+h)} }$$

$$ ={\large\lim_{h \to 0}\frac{f(x+h)g(x)-f(x)g(x)+f(x)g(x)-f(x)g(x+h)}{h\cdot g(x)g(x+h)} }$$
$$ ={\large\lim_{h \to 0}g(x)\frac{f(x+h)-f(x)}{h\cdot g(x)g(x+h)}}-{\large\lim_{h \to 0}f(x)\frac{g(x+h)-g(x)}{h\cdot g(x)g(x+h)} }$$


$$ ={\largeg(x)\frac{df}{dx}\frac{1}{(g(x))^2}-f(x)\frac{dg}{dx}\frac{1}{(g(x))^2}}$$

$$= {\large\left(\frac{df}{dx}g(x)-f(x)\frac{dg}{dx}\right)\frac{1}{(g(x))^2} = \frac{f^{\prime}g-fg^{\prime}}{g^2}}【証明終り】$$

計算の途中にある分母のところにあるｇ(ｘ＋ｈ)は、ｈ→０でｇ(ｘ)になるので、これともう１つのｇ(ｘ)と合わせて公式の分母の２乗を作るわけです。

片方の公式からもう片方の公式を導出するやり方

さて、このように積の微分公式と商の微分公式は、独立に証明できるわけです。

では、片方の公式からもう片方を導出できるでしょうか？

積の公式のほうに１／ｇ(ｘ)としてみると、これは(ｇ(ｘ))－１と考える事ができますから、合成関数のほうの微分公式を使えるのです。計算してみると次のようになります。

$$\frac{d}{dx}\frac{1}{g(x)}=\frac{d}{dx}(g(x))^{-1}=-\frac{dg}{dx}\cdot\frac{1}{(g(x))^2}$$

「ｇ(ｘ)の２乗」というものとマイナス符号が合成関数の微分のほうから出てくるわけで、これを積の微分公式に当てはめると商の微分公式になります。

商の微分公式の第１項はｇ(ｘ)を「約分」する事もできるわけですが、こちらの証明方法の観点だともともとの１／ｇ(ｘ)の形に由来するというわけです。

他方、商の微分公式のほうが先に証明されているとしましょう。この時に、簡単に前述しましたが １／ｇ(ｘ)の導関数が今度は合成関数の考え方を使わずに、商の微分公式から導出できるわけです。もちろん結果は同じです。

そのうえで、商の微分公式の中のｇ(ｘ)を、１／ｇ(ｘ)に置き換えます。ちょっとややこしいですが、微分の部分も含めて丁寧に代入して整理すると積の微分公式になるのです。

商の微分公式が分かっている状況で積の微分公式を導出するにはこのようにします。

つまり積の微分公式と商の微分公式は、独立に証明もできるし、互いに片方の公式からもう片方を導出する事も可能であるわけです。

こういった、証明の方法が複数あるという事については別に知らなくても支障はないし、大学入試の受験という観点からも証明自体が出題される頻度はかなり低いと思いますが、いくつかの方法で試してみる事は計算の練習にはなると思います。

サイト内関連記事【高校数学の微積分】

合成関数の微分公式【計算例と証明】

恭平

合成関数の微分公式の内容、具体例、証明について記します。
（英：chain rule）

目次：

  1. 公式の内容
  2. 具体的な計算例
  3. 公式の証明

■微分の定義と公式は別途に詳しくまとめています。

公式の内容

合成関数の微分公式は、ｆ(ｘ)＝ｆ(ｙ(ｘ))の形、つまり合成関数の形である時に次のように表されます。

合成関数の微分公式

$$\frac{df}{dx}=\frac{df}{dy}\frac{dy}{dx}$$ 形としてはあたかも「ｄｙ」が分母分子で「約分される」かのような形となっている事が特徴です。これは覚えるコツでもありますが、数学的にも間接的に意味のある形（例えば証明の仕方との関連）になっています。

これはどういう事かというと、次のような手順を踏めば微分ができるという事です。

  1. ｆ(ｘ)＝ｆ(ｙ(ｘ)) で ｙ＝ｙ(ｘ)とおき、
    ｆ(ｘ)＝ｆ(ｙ(ｘ)) ＝ｆ(ｙ)のように、ｙが変数であるかのような形にする。
  2. ｆ(ｙ) をｙが変数であるとみなしｙで微分する。これがｄｆ／ｄｙ
  3. ｙ＝ｙ(ｘ)を微分する。これがｄｙ／ｄｘ
  4. ｄｆ／ｄｙとｄｙ／ｄｘを掛け算する。
    （この段階では見かけ上の変数としてｘとｙが混在しています。）
  5. ｙ＝ｙ(ｘ)を代入して式の変数をｘだけにする。これがｆ(ｘ)＝ｆ((ｙ(ｘ))をｘによって微分して得る導関数に一致する。

合成関数とは、例えばｆ(ｘ) ＝ (２ｘ＋３)２のような形の関数の事で、ｙ(ｘ)＝２ｘ＋３のようにおいてｆ(ｙ(ｘ)) ＝(ｙ(ｘ))２という構造になっています。

これを微分する時に、ｆ(ｘ) ＝ (２ｘ＋３)２であれば式を展開してから普通にｘで微分する事もできますが、ｙ(ｘ)＝２ｘ＋３のｘによる微分と組み合わせて計算できる事もできるというのが合成関数の微分公式です。しかも、その組み合わせ方は「掛け算」するだけでよいというのがこの公式の意味です。

★ｙ＝ｙ(ｘ)と実際におくのは丁寧に計算する場合で、この置き換えが簡単な式である場合には頭の中で計算をしてしまう事もできます。
例えばｆ(ｘ) ＝ (２ｘ＋３)２のような関数であれば、
ｙという文字を使わずに「(２ｘ＋３)という塊とその２乗」で考えるという事です。

下図のように f(x) = cos(ωx) 【例えば cos 2x】のように表される関数の他に、$$e^{2x},\hspace{10pt}\sin^2x(=(\sin x)^2)\hspace{10pt}\frac{1}{1-x},\hspace{10pt}\sqrt{1-x^2}\hspace{10pt}$$なども、みな合成関数の仲間達です。
これらを微分する時には、普通の微分公式をそのままでは適用できない場合があります。そのようなものについては「合成関数の微分公式」で微分をして導関数を計算します。

【合成関数の微分公式】この図では、cos(ωx) という形の「合成関数」を例にして考えています。余弦関数の cos の中に、ωｘという別の関数が入っていて「合成」されているので、このような形の関数を合成関数と言います。見ての通り、微分をすると、cos が -sin になるだけでなく、ωというオマケがくっついてきます。この形の関数は、物理でもよく使いますので重要だと思います。物理では、「時間（秒）」を変数として、角速度ω[rad/s]を用いて cos(ωt), sin(ωt)といった関数を考えたりします。

具体的な計算例

この微分公式を使った計算は理論・応用ともに重要なのですが初見では計算の仕方が紛らわしく理解しにくい面もあるので、ここでは具体例についてかなり詳しく挙げておきます。

ｆ(ｘ) ＝ (２ｘ＋３)２の微分を合成関数の微分公式で計算する場合は次のようにします。

ｙ(ｘ)＝２ｘ＋３とおき、ｙをｘで微分して得る導関数ｄｙ／ｄｘ＝２と、ｙを変数とみなしたｆ(ｙ)＝ｙ２をｙで微分して得る導関数ｄｆ／ｄｙ＝２ｙ＝２(２ｘ＋３)を用意します。これらを掛け算します。

すると、ｄｆ／ｄｘ＝(ｄｆ／ｄｙ)・(ｄｙ／ｄｘ)＝２・２(２ｘ＋３)＝８ｘ＋１２です。

ｆ(ｘ) ＝ (２ｘ＋３)２＝４ｘ２＋１２ｘ＋９のように式展開して直接ｘで微分すると、ｄｆ／ｄｘ＝８ｘ＋１２となります。この結果は、合成関数の微分公式を使った場合の結果と確かに一致しています。

他の合成関数の場合の微分についても見てみましょう。特に重要度が高いのは（大学入試だけでなくその後についても）、三角関数（および三角比）や指数関数が合成関数の形になっている場合です。

三角関数の合成関数：f(x) = cos(2x)

cos(ωx) という形の関数の、さらにより具体的な関数として、
f(x) = cos(2x)という「2x」という形が余弦関数に入っている場合の微分計算を、例として手順を追って見てみましょう。
f(x) = cos(2x) = sin y の「x による微分」は、合成関数の微分公式を利用して計算できるのです。

  1. cos(2x)の 2x を y とおき、cos y を「y で」微分します。
    公式により、これは -sin y になります。
    $$\frac{d}{dy}\cos y=-\sin y$$
  2. 次に、y = 2x を x で微分します。
    これは、一次関数x の微分「１」に定数 ２ をかければよいので ２ になります。
    $$\frac{d}{dy}(2x)=2$$
  3. ｄｆ／ｄｙとｄｙ／ｄｘの積をつくります。
    これは、本当に「掛け算するだけ」の計算です。
    $$\frac{df}{dy}\frac{dy}{dx}=(-\sin y)\cdot 2 =-2\sin y$$
  4. ・・最後に、y に y = 2x を代入し、x だけの式にします。それがf(x)を x で微分して得られる導関数に等しいわけです。
    $$\frac{df}{dx}=\frac{df}{dy}\frac{dy}{dx}=-2\sin y=-2\sin (2x)$$

このタイプの微分は、イラストでも触れていますように、じつは物理でもよく使う微分計算です。
慣れてくると、cos(２ｘ) のような形である時点で微積分する時には「２」を忘れてはいけないという事にすぐに気付くようになるでしょう。

次に、指数関数が合成関数になっている場合です。考え方は上記と同じになります。
ここでは特に自然対数の底の指数関数を扱います。理論上も応用上もその場合が特に重要です。

指数関数の合成関数：ｆ(ｘ) = e(2x)

ｆ(ｘ) = e(2x)は、指数関数の変数が「2x」などになった形の合成関数です。
このタイプも、微分方程式の解法などを含めて物理学で比較的よく使う微分計算だと思います。

2x = y とおきます。
元の関数をｙで表すと、f(x)=e2x=ey(=f(y))です。

  1. y を x で微分します。$$\frac{dy}{dx}=\frac{d}{dx}(2x)=2$$※少し慣れれば、このへんは暗算でやってしまうくらいになると思います。
  2. f(y)を y で微分します。$$\frac{df}{dy}=\frac{d}{dy}e^y=e^y$$これは、e の指数関数の微分公式そのままですね。
  3. 合成関数の微分公式を適用します。
    ここでは、y を x の形に直すところまで一緒にやってしまいます。 $$\frac{d}{dx}e^{2x}=\frac{df}{dy}\frac{dy}{dx}=2\cdot e^y=2e^{2x}$$

この計算方法を見ると、一般に次のように、 $$「定数 a に対して、\frac{d}{dx}e^{ax}=ae^{ax}」$$ という事が言える事も、分かるかと思います。
f(x) = e2x の 2x が、3x でもあっても ax であっても、計算方法は同じだからです。
もっとも、これを新しく公式として「暗記」する必要は、ありません。
必要なのはあくまで普通の指数関数の微分公式と、合成関数の微分公式なのです。

注意点としては、ｙ＝ｙ(ｘ)の置き換えをした時には、最後に y を x の形に直す必要がある（場合が多い）という事だと思いますが、忘れさえしなければ数学でも物理でも、難しい計算は少ないと思います。

前述の通り、簡単な合成関数であれば置き換えは頭の中だけでやってしまっても支障ありません。

三角関数の合成関数で、少し紛らわしいタイプのものを挙げておきます。

三角関数の合成関数：ｆ(ｘ) = sin2x

三角関数を「２乗した」sin2x などの場合です。
この場合は、 sin x = y と考えて、元の関数が \(f(y)=y^2\)であると考えるのです。
従いまして、微分の計算は次のようになります。

  1. まず合成関数の微分公式に必要な材料を計算します。
    $$\frac{df}{dy}=\frac{d}{dy}y^2=2y,\hspace{10pt}\frac{dy}{dx}=\frac{d}{dx}\sin x=\frac{dy}{dx}\cos x $$
  2. ２つの材料を、掛け合わせてできあがりです。
    $$\frac{d}{dx}\sin^2x=\frac{df}{dy}\frac{dy}{dx}=2y\cos x=2\sin x \cos x = \sin 2x$$

（ここで sin 2x は、sin(2x) の事です。）
他方、sin 2x の微分は 2cos(2x) になります。（上の例のcos 2x と同様の手順です。）
sin2 x　の微分とは、少々違った結果になる事が分かるかと思います。
一見、「似てるっぽい？」かもしれませんが、計算方法を間違えないようにしたい例のひとつであるわけです。
尚、最後の結果が「x の半角」の正弦の形になる事は、三角関数の半角の公式を導出する手順で使う式（加法定理由来）を使って$$\sin^2 x=\frac{1-\cos 2x}{2}である事から、$$ $$\frac{d}{dx}\frac{1-\cos 2x}{2}=\frac{2\sin 2x}{2}=\sin 2x$$となる事と調和しています。
また、この例の微分は積の形の微分公式で計算する事も可能で、同じ結果を得ます。

他に、うっかりすると合成関数である事を見落としがちなタイプのものを挙げます。

合成関数になっている反比例関数：f(x) = １／(１－ｘ)

$$続いて、f(x)=\frac{1}{1-x}という関数の微分を考えてみましょう。$$ これも、合成関数として微分する必要があるのです。
「これのどこが合成関数？」かと思われるかもしれませんが、分母の 1-x を y と考えて合成関数と見る必要があるのです。この y = 1 – x の微分においては、定数の「１」は微分すると０になって消えます。

  1. 再び、材料作りです。
    $$\frac{df}{dy}=\frac{d}{dy}\frac{1}{y}=\frac{d}{dy}y^{-1}=-y^{-2},\hspace{10pt}\frac{dy}{dx}=\frac{d}{dx}(1-x)=-1 $$
  2. 合成関数なので掛け合わせます。
    $$\frac{d}{dx}\frac{1}{1-x}=\frac{df}{dy}\frac{dy}{dx}=(-1)(-y^{-2})=y^{-2}=\frac{1}{(1-x)^2}$$
この例の微分計算は単項式の微分公式さえ知っていれば難しくはありませんが、
「うっかり合成関数である事を見落とすと」符号を間違えてしまう例と言えます。
「マイナス１乗」の微分で１つマイナス符号がつきますが、この例では合成関数の部分に―ｘの項があるのでさらにもう１つマイナスがつき、結果はプラスになるわけです。
似たような関数でも、$$\frac{d}{dx}\frac{1}{1+x} の場合だと$$ $$\frac{d}{dx}(1+x)=1ですから、$$ $$\frac{d}{dx}\frac{1}{1+x}=-(1+x)^{-2}=-\frac{1}{(1+x)^2}$$となり、こちらはマイナスの符号がつくわけです。符号の違いは、ｘの増加に対して関数が増加するか減少するかに対応しています。

平方根がかかっている形の関数も、「１／２乗」という事ですから合成関数の形になります。

平方根を含む合成関数：\(f(x)=\sqrt{1-x^2}\)

例として、$$f(x)=\sqrt{1-x^2}$$という関数の場合は、1-x2 = y として微分計算をします。
この関数は、図形で言うと原点を中心とした半径１の円の「第１象限」の部分を関数として表したものです。

  1. 前の例と同じように材料をまず作りますが、今回再び丁寧に、２つに分けます。
    まず、かんたんなほうからです。
    $$\frac{dy}{dx}=\frac{d}{dx}(1-x^2)=-2x$$
  2. 同じく材料として、「y の平方根」の形の関数の微分を計算します。
    これは単項式の微分公式で「a=1/2」の場合を使えばいいのですが、少し分かりにくいかもしれません。
    $$\frac{df}{dy}=\frac{d}{dy}\sqrt{y}=\frac{d}{dy}y^{\frac{1}{2}}=\frac{1}{2}y^{-\frac{1}{2}}=\frac{1}{2}\frac{1}{\sqrt{y}}$$
  3. ２つの材料がそろえば、あとは掛け合わせて、ｙを x の関数の形に戻すだけです。
    $$\frac{d}{dx}\sqrt{1-x^2}=\frac{df}{dy}\frac{dy}{dx}=(-2x)\frac{1}{2}y^{-\frac{1}{2}}=\frac{-x}{\sqrt{y}}=\frac{-x}{\sqrt{1-x^2}}$$

この例で用いている「平方根の微分」は慣れないと、とっつきにくい場合も多いかと思います。
ただ、このタイプの関数の微分は物理でもよく使いますので、知っておくと便利です。

物理や工学等の理論でこれらの関数の微積分を使用するには「これは合成関数の形だから・・」という説明は省略して結果だけ書く事が普通ですので、その意味でも計算の仕方に慣れておく事は大事かと思います。計算に慣れれば簡単な合成関数であれば「公式」としての形を特に暗記しようと努めなくても自然に計算できるようになります。

公式の証明

合成関数の微分公式の証明は次のようにします。

f(ｘ) = ｆ(ｙ(ｘ)) 、 ｙ = ｙ(ｘ) である時、まず次のように考えます。

  • ｆ(ｙ(ｘ))の導関数を、定義の極限を含む形で書きます。
  • ｆの中の変数部分ｙ(ｘ＋ｈ)について、ｙ(ｘ＋ｈ)＝ｙ(ｘ＋ｈ)－ｙ(ｘ)＋ｙ(ｘ)と変形します。


$$\frac{d}{dx}f(x)=\lim_{h \to 0}\frac{f(y(x+h))-f(y(x))}{h}=\lim_{h \to 0}\frac{f(y(x+h)-y(x)+y(x))-f(y(x))}{h} $$

次に、ｙ(ｘ＋ｈ)－ｙ(ｘ)という項を「掛けて割る」操作をします。これは値としては「１」を掛ける操作なので自由に行ってよいのです。

$$ \frac{d}{dx}f(x)=\lim_{h \to 0}\frac{f(y(x+h)-y(x)+y(x))-f(y(x))}{h}\cdot \frac{y(x+h)-y(x)}{y(x+h)-y(x)}$$

$$=\lim_{h \to 0}\frac{f(y(x+h)-y(x)+y(x))-f(y(x))}{y(x+h)-y(x)}\cdot\frac{y(x+h)-y(x)}{h}$$

ここで、ｚ＝ｙ(ｘ＋ｈ)－ｙ(ｘ)とおきます。そのようにおかなくても証明できますが、見やすくするという意味です。ｚに置き換わる部分は３つあり、ｄｆ／ｄｘは次のような形になります。

$$\frac{d}{dx}f(x)=\lim_{h \to 0}\frac{f(z+y(x))-f(y(x))}{z}\cdot\frac{z}{h}$$

ここで、ｈ→０のとき、limｈ→０ｚ＝limｈ→０（ｙ(ｘ＋ｈ)－ｙ(ｘ)）＝ｙ(ｘ)－ｙ(ｘ)
＝０ですから、ｈとｚの両方を０に近づけるという意味で 「limｈ,ｚ→０ 」と書く事ができます。このときに、

$$\lim_{h \to 0}\frac{z}{h}=\lim_{h \to 0}\frac{y(x+h)-y(x)}{h}=\frac{dy}{dx}$$

である事に注意し、ｙ＝ｙ(ｘ) を変数とみなしてｙと書くと次のようになります。

$$\frac{d}{dx}f(x)=\lim_{h,z \to 0}\frac{f(z+y)-f(y)}{z}\cdot\frac{z}{h} =\frac{df}{dy}\frac{dy}{dx}【証明終り】$$

このように、１つの導関数を別の導関数の積で表せるという結果になるのです。

２項定理

恭平

２項定理（あるいは「２項展開」）とは、
(ｘ＋ｙ)ａの形の式を展開した時にどのようになるかを表した式です。

指数の部分ａは自然数である事も多いですが、一般の実数で同じ形に展開できます。（ただしａが自然数でない場合は有限の数の項で終わらず無限級数になる場合があります。）

目次：

  1. 指数が自然数の場合
  2. 指数が実数の場合（一般２項定理）

指数が自然数の場合

まず、簡単なのはｎを自然数として、(ｘ＋ｙ)ｎの形の式を展開した場合です。
ただし簡単とは言っても、任意の自然数ｎについてどのようなものになるかを知るには順列と組み合わせの知識が必要です。

ｎ＝２の場合、(ｘ＋ｙ)２＝ｘ２＋２ｘｙ＋ｙ２　であり、

ｎ＝３の場合、(ｘ＋ｙ)３＝ｘ３＋３ｘ２ｙ＋３ｘｙ２＋ｙ３　です。

ｎが小さい場合は直接に計算もできますが、じつは公式として書けるというのが２項定理です。

２項定理（指数が自然数の時）

$$(x + y)^n=x^n+n\mathrm{C} _1x^{n-1}y+{}_n \mathrm{C} _2x^{n-2}y^2+{}_n \mathrm{C} _3x^{n-3}y^3+\cdots+{}_n \mathrm{C} _{n-1}xh^{n-1}+y^n$$ $$ =x^n +nx^{n-1}y+\frac{n(n-1)}{2}x^{n-2}y^2+\frac{n(n-1)(n-2)}{3!}x^{n-3}y^3+\cdots+nxy^{n-1}+y^n$$

★順列や組み合わせを学ぶと必ず出てくるものですが、びっくりマークが「！」ついている「3！」は「３の『階乗』」で、3！= 3・2・1 = 6 を表します。4 の階乗なら、4！=4・3・2・1 = 24。ここではあまり関係ないですが「ゼロの階乗」は0！= 1 と「定義」します。

このようになる理由自体は単純で、直接の式の展開を考えてみるのです。

x とｙ を何個選ぶかの「組み合わせ」を考えます。

２項定理と組み合わせ
３つの場所の中からｘを１つ選ぶと、残り２つはｙで決定するので係数は「組み合わせ」の数として決定します。

ｎ＝２やｎ＝３の場合を考えてみると分かりやすいと思いますが、ｘｙやｘ２ｙの項の係数は結局どういう理由で決まるのかというと、式展開した時にそれらの項が「何個」あるかで決まっています。

ｎ＝３のときのｘ２ｙの項については「３つの項の中からｘを２個、ｙを１個選ぶ方法」の数に等しいのです。これは、組み合わせで表現できます。

少し分かりにくい場合は、３つの場所①②③を考えて、２つ選ぶという場合を考えてみてください。その２つの場所からｘをぶという考え方でも組み合わせの総数になります。

３つの中から３個ともｘ、３個ともｙを選べばｘ３とｙ３の場合であり、そのような組み合わせは１通りだけで実際それらの項の係数は１になります。

つまり、(ｘ＋ｙ)ｎのｘｍｙｎ－ｍの項の係数がｎＣｍになるというのが２項定理の内容です。
組み合わせの性質により、ｎＣｎ－ｍ＝ｎＣｍになります。３乗の展開式において係数が１、３，３、１の順で並ぶのはそのためです。

４乗の場合の展開式を計算してみると、４Ｃ１＝４Ｃ３＝４、４Ｃ２＝６であるので、(ｘ＋ｙ)４＝ｘ４＋４ｘ３ｙ＋６ｘ２ｙ２＋４ｘｙ３＋ｙ４　です。
これは、３乗の展開式に（ｘ＋ｙ）をかけてみても同じ結果になります。

指数が実数の場合（一般２項定理）

上記の指数が自然数の場合の形の式と全く同じ形が、指数が実数一般の場合でも成立する事を特に指して一般２項定理（もしくは一般２項展開）と言います。

この場合はどうやって示すのかというと、結論を言うとマクローリン展開を使います。マクローリン展開とは微積分を利用した関数の無限級数展開の１つで、高校では教えない場合も多いので高校生であれば覚える必要はありません。（テイラー展開の特別な場合がマクローリン展開です。）

参考までに述べておくと一般２項定理の証明は次のようになります。

一般２項定理の証明

a が自然数でない時、\((1+x)^a\hspace{5pt}(|x|＜1)\)に対して適用して、マクローリン展開を適用すると、 $$(1+x)^a=1+ax+\frac{a(a-1)}{2}x^2+\frac{a(a-1)(a-2)}{3!}x^3+\frac{a(a-1)(a-2)(a-3)}{4!}x^4+\cdots$$ r ＜ s および s ≠ 0 の任意の実数 r と s の組に対して |x|＜1 の範囲に x = r/s となる x が存在するので、 $$\left(1+\frac{r}{s}\right)^a=1+a\frac{r}{s}+\frac{a(a-1)}{2}\frac{r^2}{s^2}+\frac{a(a-1)(a-2)}{3!}\frac{r^3}{s^3}+\cdots$$ $$\left(1+\frac{r}{s}\right)^a=\left(\frac{s+r}{s}\right)^a=\frac{(s+r)^a}{s^a}に注意して、$$ 上式の両辺にsａ（これは有限の値）をかけます。 $$(s+r)^a=s^a+ars^{a-1}+\frac{a(a-1)}{2}r^2s^{a-2}+\frac{a(a-1)(a-2)}{3!}r^3s^{a-3}+\cdots$$ というわけで、a が自然数の場合とも合わせて、一般２項定理が成立する事を意味します。（証明終）
この証明でややこしくて面倒なのは、\((1+x)^a\)のマクローリン展開が可能な x の範囲が |x|＜1 という形で限定されているため、最初からマクローリン展開で直接に一般２項定理を示そうとすると話がこじれるところでしょう。

冒頭でも少し触れましたが、このように形としては指数が自然数でもそうでなくても同じ関係式が成立しますが、指数が負の数などの場合では項が延々とずっと続き無限級数になります。（単なる式の展開が無限級数とか微積分との関連もあるというのは、少し意外に思う人もいるかもしれません。）

２項定理が成立するとすると、単項式の微分公式が (ｘａ)’ ＝ｎｘａ－１となる理由が分かりやすくなるという利点があります。（ただしａが実数の場合には、一般２項定理は微分公式の証明にはなりません。指数が実数の場合の単項式の微分公式の証明は、普通は対数関数の微分公式を利用します。）

必要・十分条件の考え方

恭平

必要条件、十分条件、必要十分条件の意味・覚え方・使い方などについて説明します。
必要条件と十分条件は対になっている考え方であり、ともに成立する場合には必要十分条件と言います。
（英：必要条件 necessary condition　十分条件 sufficient condition
　必要十分条件 necessary and sufficient condition）

ここでは高校数学で必要な知識を説明します。

目次：

  1. 考え方と内容
  2. 【図での覚え方】論理式と集合との関係
  3. 証明問題・計算での使い方

★必要条件や十分条件そのものについて問う出題は高校数学特有のものですが、用語や考え方自体は大学数学でも使います。ただし、物理や工学などでは基本的には使用しません。

考え方と内容

「ＰならばＱ」という関係（「論理式」）が成立する時、ＰはＱの十分条件であると言います。
また、ＱはＰの必要条件であると言います。
記号では矢印記号「⇒」を使って「ならば」の部分を表し、 Ｐ ⇒ Ｑと書きます。

例えば「『ある実数が偶数である』ならば『その実数は自然数である』」といった感じです。
一般の定理などはそのような形をとっています。例えば三平方の定理は「『ある三角形が直角三角形である』ならば『斜辺と残り２辺の長さをそれぞれｃ、ａ、ｂとしてｃ２＝ａ２＋ｂ２である』」という形です。
【※後述しますが三平方の定理に関してはこの逆も成立し、必要十分条件になります。】

この「ＰならばＱ」とは、「Ｐが成立するなら、必ずＱも成立している」という意味です。「必ず」というところがポイントで、例外は１つでもあってはいけないというのが数学での表現上のルールです。

「ＰならばＱ」Ｐ ⇒ Ｑ　と「ＱならばＰ」Ｑ ⇒ Ｐ　が両方とも成立する時、ＰはＱの必要十分条件であると言います。（この時、ＱのほうもＰの必要十分条件であると言います。）記号は、両方向に向いた矢印の「⇔」を使い、Ｐ ⇔ Ｑ と書きます。

十分条件、必要条件、必要十分条件

数学において「ＰならばＱ」　Ｐ⇒Ｑ　の関係が成立する時、次の呼び方をします。

  1. ＰはＱの「十分条件」
  2. ＱはＰの「必要条件」
  3. Ｐ ⇒ Ｑ　かつ　Ｑ ⇒ Ｐのとき、
    ＰはＱの「必要十分条件」（ＱはＰの必要十分条件）

★「必要条件」のほうの名称の由来ですが、Ｐ ⇒ Ｑ の関係が成立する時、「Ｑが偽であるならばＰも偽である」という関係が成立するためと思われます。つまりＰが真であるためには少なくともＱは真でなければならず、Ｑが偽でＰが真である場合はあり得ないという事です。（他方Ｐ ⇒ Ｑ の時に、Ｑが真でもＰが真である事は確定しません。Ｑが真でＰが偽の場合はあるのです。そこが十分条件と異なります。）
この関係は、後述する図によるイメージで理解が進むかと思います。

論理式の説明

Ｐ ⇒ Ｑ の関係が成立する時、「Ｑが成立するためには、Ｐが成立すれば十分である」といった表現をする事もあります。また、必要条件のほうに着目して「Ｐが成立するためには、Ｑが成立する事が必要である」と言う事もあります。

また文章の表現として、Ｐ ⇒ Ｑ の関係について「ＱはＰが成立するために『必要ではあるが十分ではない』」という表現がなされる場合もあります。これは、特に Ｑ ⇒ Ｐ は成立しない事が判明している場合に使われる事が多いです。（後にも触れますが、Ｐ ⇒ Ｑが判明しているけれどＱ ⇒ Ｐかどうかはまだ不明であるという場合もあり得ます。）

★このときのＰやＱは数学的に意味のあるものを考えます。
「今朝は晴れだった」とか「この理論は美しい」とかそういう文章の類は入れないわけです。

もう１つ例を挙げてみます。
Ｘが自然数の時、「Ｘが４の倍数である事」は「Ｘが偶数である事」の十分条件です。

これは、「Ｘが４の倍数」であれば必ず「Ｘは偶数」であるからです。
「Ｘが４の倍数である」 ⇒「Ｘは偶数である」　は、成立しています。

他方、Ｘが偶数であっても「必ず」４の倍数とは言えません。これは、例えば偶数であっても２や６といった数は４の倍数ではないからです。このように出てきてしまう「例外」の具体例の事を、数学の用語として反例と言います。

「Ｘが６の倍数である」事も「Ｘが偶数である」事の十分条件の１つです。
６の倍数６，１２，１８，２４、・・・は例外なく、必ず偶数であるからです。
つまり「Ｘが６の倍数である」 ⇒「Ｘは偶数である」　も成立しています。

このように、十分条件というものは複数あり得ます。

必要条件についても同様で、１つではなく複数あり得ます。
例えばここでの例で「Ｘが偶数である」を「Ｘが２以上の自然数である」といったものに変えても同様に
「Ｘが４の倍数の自然数である」 ⇒「Ｘは２以上の自然数である」　
は成立するので、Ｘが自然数の時に「Ｘが２以上の自然数である」事も「Ｘが４の倍数である」事の必要条件になります。

【図での覚え方】論理式と集合との関係

これら十分条件と必要条件の上手な捉え方として、ある変数が集合の元（要素）である事に関する論理式を考え、さらに図に描くという方法があります。この方法は、論理式の構造の理解のために大変便利です。

例えば「『ｘが集合Ｂに属する（Ｂの元である）』ならば『そのｘは集合Ａに属する』」という事が正しいとしましょう。この時、集合Ａと集合Ｂの包含関係は「ＡがＢを含む（Ａ⊃Ｂ）」という事になります。これは、この関係が成り立つという事は「ｘがＢに属するのであれば『必ず』そのｘはＡに属してもいる」という意味であるからです。

これらの集合が例えば平面上の領域（点の集まり）であれば、これは図形に描けます。絵としては、穴などがない領域Ａの中に完全に領域Ｂが含まれてしまっている場合です。この時に、領域Ａに完全に含まれてしまっている領域Ｂが、「十分条件」のイメージです。

逆に、相手方である領域Ｂを含んでいる大きなほうの領域Ａが、「必要条件」のイメージです。

★ここで、もしもｘ∊Ｂ ⇒ ｘ∊Ａ という情報だけがあって領域ＡとＢの実際の様子は分からない場合には、論理式の逆の「ｘ∊Ａ⇒ｘ∊Ｂ」が成立するかはその段階では「不明」という事になります。
ただし、その場合でも領域Ａが領域Ｂを含んでいる事は確定しています。しかし、Ａ⊃Ｂであると同時にＢ⊃Ａでもある可能性、つまり領域ＡとＢが完全に一致している場合も考えられるわけです。

図による説明
Ｐ ⇒ Ｑ という事は、「Ｑがもし偽であればＰも偽である」という事で、図で言うと領域Ａに含まれていない点（つまり領域Ａの外にある点）は領域Ｂにも含まれていないという意味になります。このような事も図で見ると理解しやすくなるかと思います。

領域ではなくて数直線上の区間で考えても同じで、
例えば実数ｘが閉区間 [０,１／２] に含まれるならば、ｘは閉区間 [－１,１]に含まれています。
記号で書くとｘ∊ [０,１／２] ⇒ ｘ∊ [－１,１] という事であり、
ｘ∊ [０,１／２] は ｘ∊ [－１,１] であるための「十分条件」であり、
ｘ∊ [－１,１]はｘ∊ [０,１／２]であるための「必要条件」です。
閉区間同士の包含関係については、[－１,１] が [０,１／２] を含んでおり [－１,１] ⊃ [０,１／２] です。

証明問題・計算での使い方

三平方の定理を証明する時は、まずは前提となる「直角三角形である」という条件が正しいとして、その時に必ず３辺の関係がｃ２＝ａ２＋ｂ２となる事を示すわけです。

すると、その証明によって
『三角形が直角三角形である』⇒『斜辺と残り２辺の長さをｃ、ａ、ｂとしてｃ２＝ａ２＋ｂ２である』
という論理式が真であるという事になるわけです。

しかし逆に、
『三角形の辺の関係式ｃ２＝ａ２＋ｂ２が成立する』⇒『三角形が直角三角形である』
という事が正しいかはこの時点では分かりません。
この段階ではこの逆の形の論理式が「真か偽かも分からない」という事です。

★Ｐ ⇒ Ｑ が成立している時に矢印の先のほうのＱを必要条件と呼ぶわけですが、この時に Ｑ ⇒ Ｐ が成立するかどうかが判明しているとは限りません。
一般には特別な条件が明示されていない限りは、Ｐ ⇒ Ｑの成立からＱ ⇒ Ｐの真偽を直ちに判定する事はできないので、その真偽を明確にするために「証明」という作業を行います。

従って、それが真か偽かもまた証明によって調べる必要があります。
今度は辺の長さの関係を前提として（正しいものとして）証明を行うわけです。

結論を言うと三平方の定理の「逆」である
『三角形の辺の関係式ｃ２＝ａ２＋ｂ２が成立する』⇒『三角形が直角三角形である』
も、確かに成立します。証明できるという事です。
という事はＰ ⇒ Ｑ の形に対してＱ ⇒ Ｐの形も成立しているので、三平方の定理は「必要十分条件」である Ｐ ⇔ Ｑ の形となるわけです。

このように「必要十分条件である事を証明せよ」という問題の場合（入試問題以外でも）、
まず Ｐ ⇒ Ｑ を証明し、次に Ｑ ⇒ Ｐ も証明して Ｐ ⇔ Ｑ であると結論付けるのが一般的手法です。

このような形で三平方の定理の逆も成立する事を証明できます。

通常の実数や文字式等の計算での式の変形も、じつは細かく言うと「必要十分条件」の関係です。

ｘ－ｙ＝０の時、ｘ＝ｙであるわけですが、
細かい事を言うとｘ－ｙ＝０⇒ｘ＝ｙかつｘ＝ｙ⇒ｘ－ｙ＝０であり、
ｘ－ｙ＝０⇔ｘ＝ｙというわけです。
そのため、式変形をする時に必要十分条件の記号⇔を使う事があります。

注意が必要な例として、平方根と２乗の関係があります。次の関係を見ましょう。ｘは実数とします。

$$x=\sqrt{2}\Rightarrow x^2=2$$

この論理式は成立します、しかし注意が必要なのは、この場合には「必要十分条件」で結ぶ事はできないという事です。それをやってしまうと、論理式は「偽」になってしまいます。理由は簡単で、２乗して２になる数（実数）は、\(\sqrt{2}\)は確かに当てはまるのですが、もう１つ負の数のほうの\(-\sqrt{2}\)があるためです。

$$特に条件が無い場合、x^2=2\Rightarrow x=\pm\sqrt{2}$$

この関係の逆は成立します。そのため、必要十分条件で結ぶのであれば次のようにする必要があります。

$$x^2=2\Leftrightarrow x=\pm\sqrt{2}$$

これを確実に見るには、ｘ２＝２ ⇔ (ｘ＋\(\sqrt{2}\))(ｘ－\(\sqrt{2}\))＝０という因数分解された形にするとよいでしょう。【この「因数分解の形にする」という式変形は、必要十分条件で結ばれます。】

少し話が込み入りますが、もしも「ｘは正の数」という条件があるのであれば、上記の右方向だけの \(x=\sqrt{2}\Rightarrow x^2=2\) は必要十分条件で結んでも間違いではありません。これは「ｘ＞０かつ\(x^2=2\)」という具合に、条件自体が変わるためです。

このように、一般の実数等での式変形であれば必ず必要十分条件になるわけではなく、時々片側にのみ
「ならば」記号の矢印⇒が成立する場合もあります。その点だけは少しだけ注意が必要になります。

和積・積和・倍角・半角の公式

恭平

三角関数の積和の公式、和積の公式、倍角の公式、半角の公式という一連の公式は互いに本質的に異なるものではなく、全て三角関数の加法定理から導出されるものです。
（英：倍角の公式 double-angle formula　半角の公式 half-angle formula）
（和積の公式と積和の公式は、英語では加法定理の一部だと捉えられる事も多いようです。）

目次：

  1. 公式の内容
  2. 証明①：積和の公式
  3. 証明②：和積の公式
  4. 証明③：倍角と半角の公式

★高校数学の中の位置付けだと、まずこれらの公式よりも大事なのは加法定理であると言えます。これらの公式は、じつは加法定理さえ覚えていれはその場で割と簡単に導出が可能であるからです。
これらの和積の公式等を暗記するにしても、まずは加法定理との形との対応から慣れていき、入試問題などを解いて練習しながら覚えていくのがよいと思います。

公式の内容

積和の公式、和積の公式、倍角の公式、半角の公式の内容を順に記すと次のようになります。これらは切り離された別々の公式ではなくて、本質的には加法定理を目的に応じて使いやすいように変形したものです。

積和の公式

次の正弦と余弦の「積」に関する４式を言います。【三角関数の積の形を和にする公式です。】$$\sin A \cos B=\frac{\sin (A+B)+\sin (A-B)}{2}$$ $$\cos A \sin B=\frac{\sin (A+B)-\sin (A-B)}{2}$$ $$\cos A \cos B =\frac{\cos (A+B)+\cos (A-B)}{2}$$ $$\sin A \sin B =-\frac{\cos (A+B)-\cos (A-B)}{2}$$

和積の公式

次の正弦と余弦に関する４式を言います。【三角関数の和や差の形を積にする公式です。】$$\sin C +\sin D =2\sin\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)$$ $$\sin C -\sin D =2\cos\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)$$ $$\cos C +\cos D =2\cos\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)$$ $$\cos C -\cos D =-2\sin\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)$$ 後述しますが、ここで使っているＣやＤは、加法定理や上記の積和の公式でのＡとＢを使ってＣ＝Ａ＋Ｂ, Ｄ＝Ａ－Ｂとおいたものです。

倍角の公式

正弦と余弦に関する倍角の公式は次の２式です。 $$\sin 2A=2\sin A\cos A$$ $$\cos 2A=\cos ^2A-\sin ^2A$$ 余弦のほうはcos２Ａ＝２cos２Ａ－１＝１－２sin２Ａとも表せます。
正接の倍角の公式は tan２Ａ＝(sin２Ａ)／(cos２Ａ)で計算します。

半角の公式

正弦と余弦に関する半角の公式は次の２式です。 $$\cos A=\pm\sqrt{\frac{1+\cos 2A}{2}}$$ $$\sin A=\pm\sqrt{\frac{1-\cos 2A}{2}}$$ プラスマイナスの符号は角度に応じて適切なほうを選びます。
Ａ＝Ｘ／２といった置き換えをすると「半角」という事をより明確にもできます。
正接の半角の公式も正弦を余弦で割って計算できます。

ところで、これらの式の数を合計すると１２個ありますね。これらを１つ１つ、別々の公式として暗記するのは大変です。そのため、もとになっている加法定理を変形したものであるという見方のほうが勧められます。

公式の導出①
積和の公式、和積の公式、倍角の公式などは、加法定理をもとにして作る公式です。

三角関数の加法定理については証明も含めて別途に詳しく述べていますが、正弦と余弦について結果だけ記すと次のようになります。

加法定理
  1. sin(Ａ＋Ｂ)＝sinＡcosＢ＋cosＡsinＢ
  2. sin(Ａ－Ｂ)＝sinＡcosＢ－cosＡsinＢ
  3. cos(Ａ＋Ｂ)＝cosＡcosＢ－sinＡsinＢ
  4. cos(Ａ－Ｂ)＝cosＡcosＢ＋sinＡsinＢ

これらを組み合わせると和積・積和の公式が導出され、角度の１つを置き換えると倍角の公式になります。
半角の公式については倍角の公式を変形して導出する事になります。

証明①：積和の公式

加法定理の４式のうち、正弦同士、余弦同士を見ると、２つの項は符号が違うだけで同じ形をしています。この事を使います。

まず、正弦についての加法定理の２式を加えてみましょう。

sin(Ａ＋Ｂ)＋sin(Ａ－Ｂ)＝sinＡcosＢ＋cosＡsinＢ＋sinＡcosＢ－cosＡsinＢ＝２sinＡcosＢ

本質的にはこれだけでよくて、和積の公式も積和の公式も、本質的には本来はこの同じ形の関係式です。ただ、三角関数の積を和に直すか、和を積に直すかで少しだけ形を変えて「公式」としているだけです。まず、積和の公式は上記の式の両辺を単純に２で割って、積が和の形になるようにします。

$$\sin A \cos B=\frac{\sin (A+B)+\sin (A-B)}{2}$$

他の３式も、加法定理の２式を加える・２式の差をとる事で導出します。

$$\sin (A+B)-\sin (A-B)=2\cos A \sin B\Leftrightarrow\cos A \sin B=\frac{\sin (A+B)-\sin (A-B)}{2}$$

$$\cos (A+B)+\cos (A-B)=2\cos A \cos B\Leftrightarrow\cos A \cos B =\frac{\cos (A+B)+\cos (A-B)}{2}$$

$$\cos (A+B)-\cos (A-B)=-2\sin A \sin B\Leftrightarrow\sin A \sin B =-\frac{\cos (A+B)-\cos (A-B)}{2}$$

証明②：和積の公式

では、和の形を積に直している和積の公式は、どのように出すのでしょう。

じつは使う式は全く同じで「変数の置き換え」をするのです。

一般的には次のようにします。
まずＡ＋Ｂ＝Ｃ，Ａ－Ｂ＝Ｄのようにおき直します。
次にこの２式を加えると ２Ａ＝Ｃ＋Ｄ ⇔ Ａ＝(Ｃ＋Ｄ)／２
片方からもう片方を引くと２Ｂ＝Ｃ－Ｄ ⇔ (Ｃ－Ｄ)／２　
このようになる事を使って、式を整理して公式としています。

$$\sin (A+B)+\sin (A-B)=2\sin A \cos B においてA=\frac{C+D}{2}, \hspace{5pt}B=\frac{C-D}{2}とおくと$$

$$\sin C +\sin D =2\sin\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)$$

加法定理の２式の和ではなく「差」をとると、正弦の差を積に直す形の公式が得られます。

$$\sin (A+B)-\sin (A-B)=2\cos A \sin B においてA=\frac{C+D}{2}, \hspace{5pt}B=\frac{C-D}{2}を代入します。$$

$$\sin C -\sin D =2\cos\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)$$

余弦のほうについても、加法定理の２式を加える・差をとる事で公式を導出します。まず余弦に関する和積の公式の和の形のほうのものは次のようになります。

$$\cos (A+B)+\cos (A-B)=2\cos A \cos B においてA=\frac{C+D}{2}, \hspace{5pt}B=\frac{C-D}{2}を代入します。$$

$$\cos C +\cos D =2\cos\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)$$

差の形のほうは次のようになります。

$$\cos (A+B)-\cos (A-B)=2\cos A \cos B においてA=\frac{C+D}{2}, \hspace{5pt}B=\frac{C-D}{2}を代入します。$$

$$\cos C -\cos D =-2\sin\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)$$

具体例：
例えば、唐突に sin７５°＋sin１５°の値はいくらかと聞かれたらこの公式を使えば即座に答えは出るという事です。（こういう問いは理解度を試すための問題で、高校数学以外ではあまりやりません。）
(７５°＋１５°)÷２＝４５° と (７５°－１５°)÷２＝３０° の正弦の値を使います。$$\sin 75°＋\sin 15°＝2(\sin 45°)(\cos 30°)=2\cdot \frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{6}}{2}$$ 加法定理で７５°＝３０°＋４５°などとして加法定理を使って計算しても結果は同じです。ただ、和積の公式を知っていると多少計算は速く済みます。

証明③：倍角と半角の公式

次に倍角の公式と半角の公式と呼ばれる式の導出方法です。
これらもまた別々のものではなく、本質的には同じ式であるものを変形したものです。

公式の導出②
余弦の半角の公式は余弦の倍角の公式から得ますが、正弦の半角の公式も同様に余弦の倍角の公式から導出されます。

まずは倍角の公式から見ましょう。

sin２Ａ＝２sinＡcosＡ　という式ですが、
じつはこれは、加法定理で２つの角度についてＡ＝Ｂとしているだけなのです。
余弦のほうの倍角の公式も、やり方は同じです。

つまり次のようにします。
sin(Ａ＋Ｂ)＝sinＡcosＢ＋cosＡsinＢ　において Ａ＝Ｂとして sin２Ａ＝２sinＡcosＡ
cos(Ａ＋Ｂ)＝cosＡcosＢ－sinＡsinＢ　において Ａ＝Ｂとして cos２Ａ＝cos２Ａ－sin２Ａ

余弦のほうは、cos２Ａ＋sin２Ａ＝１を使ってcos２Ａ＝２cos２Ａ－１、もしくはcos２Ａ＝１－２sin２Ａとも表せます。

次に半角の公式の導出です。

このページで紹介している公式のうち半角の公式についてだけは加法定理から直ちには出せず、余弦のほうの倍角の公式を変形する事になります。
（ただし倍角の公式が簡単に出るので、導出に手間はかからないはずです。）

cos２Ａ＝２cos２Ａ－１ ⇔ cos２Ａ＝(cos２Ａ＋１)／２　から余弦の半角の公式、
cos２Ａ＝１－２sin２Ａ ⇔ sin２Ａ＝(cos２Ａ－１)／２　から正弦の半角の公式を得ます。
２乗がありますので、平方根を考える事になります。

$$\cos A=\pm\sqrt{\frac{1+\cos 2A}{2}}$$

$$\sin A=\pm\sqrt{\frac{1-\cos 2A}{2}}$$

平方根をとる時に一般の場合では符号が確定しませんが、具体的に例えばプラスの鋭角に対する「半分の角度」を考えるのであれば、余弦も正弦もプラスのはずなので、プラス符号のほうをとります。

このように倍角・半角の公式もまた、基本は本質的に加法定理によるものであるわけです。加法定理さえ覚えておけば、例えば倍角の公式は暗記しなくても即座に出てきますし、半角の公式で正弦・余弦の公式がともに余弦を使って表される事も理解できて覚えやすいはずなのです。

尚、角度Ａに対する３倍の３Ａを考えた３倍角の公式、４倍角の公式、・・なども一応存在します。
ただしこれらも同様に、いずれも加法定理から出せる関係式ですので一般的には暗記しなくてもよい場合も多いと思われる事項です。
参考までに、複素数に関するド・モアブルの定理を使うと、そういった三角関数の３倍角の公式などの形を比較的容易に知る事も可能です。

積和の公式や倍角の公式などは、大学入試で直接計算を問われる場合以外には、三角関数に関する積分の計算に使う事が比較的多いように思います。例えば、sinｘcosｘの原始関数（微分すると対象の関数となる関数）は微分の公式だけからは即座には分かりにくいので、倍角の公式を思い出してこれを (sin 2ｘ)／２の形にして積分の計算をするといったものです。

また、物理学で２つの正弦波の重ね合わせをするときも、和積の公式を知っていると即座に結果を計算できるので便利です。

この手の三角関数の微積分での変形計算は大学入試でも問われるかもしれませんが、大学数学の微積分の一部でも重要である場合があります。ただし繰り返しになりますが、加法定理とこれらの公式の導出の方法の大筋さえ覚えておけば、もし公式を忘れてしまってもすぐにその場で計算できるようになります。

三角関数の加法定理【証明】

恭平

三角関数の加法定理とは、三角関数の角度部分を和や差の形で表す時、個々の角度に対する三角関数の積と和などの組み合わせで計算できるという公式です。
（英：compound angle formulae）

目次：

  1. 定理の内容
  2. 証明
  3. 具体例・応用例・覚え方
  4. 外積を使った証明方法

高校数学の中では、その後に続く理論でも使うという意味では加法定理は重要な部類に入る関係式の１つであると言えます。

尚、対数関数についても「加法定理」という言葉を使用する事がありますが、ここでは三角関数についてのものを述べます。

定理の内容

■ 正弦と余弦の加法定理４式　■ 正接関数の加法定理

正弦と余弦の加法定理４式

三角関数の加法定理は、正弦・余弦・正接について存在しますが正弦と余弦の４式は次のようになります。

加法定理（正弦関数と余弦関数）

２つの角度をＡとＢとすると、次の関係式が成立します。

  1. sin(Ａ＋Ｂ)＝sinＡcosＢ＋cosＡsinＢ
  2. sin(Ａ－Ｂ)＝sinＡcosＢ－cosＡsinＢ
  3. cos(Ａ＋Ｂ)＝cosＡcosＢ－sinＡsinＢ
  4. cos(Ａ－Ｂ)＝cosＡcosＢ＋sinＡsinＢ

これらの角度の範囲は、三角関数での定義を使用するなら任意の実数になります。
負の数や２直角\(\pi\)を超える値になってもよいし、それらをＡやＢとして代入する事もできます。

これら４式について、１つの符号を反転させればもう１つの式が得られるので
「実質は正弦と余弦について１つずつ」の２つであると見なすことも可能です。

これは、－Ｂ＝＋Ｂのように考えて式をまとめても支障はないという意味です。
sin(Ａ－Ｂ)＝sin(Ａ＋(－Ｂ))＝sinＡcos(－Ｂ)＋cosＡsin(－Ｂ)＝sinＡcosＢ－cosＡsinＢ
cos(Ａ－Ｂ)＝cos(Ａ＋(－Ｂ))＝cosＡcos(－Ｂ)－sinＡsin(－Ｂ)＝cosＡcosＢ＋sinＡsinＢ
のように導出はすぐにできるので、覚えるのは４式ではなく２式でも計算はできます。

４式でやるか２式でやるかは、理解しやすいほう・覚えやすいほうの考え方でよいと思います。
１つの角度の符号を反転させて別の式の導出をするという考え方は証明でも使います。
また、証明の時に最初に証明されるのはcos(Ａ－Ｂ)の式である都合上、最初から４式で考えたほうが理解しやすいという考え方もあります。

正接関数の加法定理

正接関数にも加法定理はありますが、正接は (正弦)／(余弦)で考えれば済む事と、使用頻度が比較的少ない事からここでは参考までに記しておきます。

正接関数の加法定理

正接関数の加法定理の式は次の通りです： $$\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A\tan B}$$ $$\tan (A-B)=\frac{\tan A-\tan B}{1+\tan A\tan B}$$

これらの式は、正弦関数と余弦関数の加法定理が成立するという前提で示されます。

$$\tan (A+B)=\frac{\sin (A+B)}{\cos (A+B)}=\frac{\sin A \cos B +\cos A\sin B}{\cos A\cos B-\sin A \sin b}=\large{=\frac{\frac{\sin A}{\cos A}+\frac{\sin B}{\cos B}}{1-\frac{\sin A}{\cos A}\frac{\sin B}{\cos B}}}$$
$$\tan (A-B)=\frac{\sin (A-B)}{\cos (A-B)}=\frac{\sin A \cos B -\cos A\sin B}{\cos A\cos B+\sin A \sin b}=\large{=\frac{\frac{\sin A}{\cos A}-\frac{\sin B}{\cos B}}{1+\frac{\sin A}{\cos A}\frac{\sin B}{\cos B}}}$$

このようになる事が根拠であり、
後者の式は tan(－θ)＝tanθの関係を前者の式の結果に代入する事でも得られます。

証明

■ 考え方：三角比の範囲の場合
■ 一般角の場合①　余弦 cos (Ａ－Ｂ)の式の証明
■ 一般角の場合②　残り３式の導出　

考え方：三角比の範囲の場合

証明はいきなり一般の角度の場合でもできるのですが、まず図形上の考え方を見るために０°～９０°の範囲における三角比の中で加法定理が成立する事の説明をしましょう。

図のように単位円の「第１象限」の部分で２つの角度の考えて三角形を作ります。
ここで、２つの角度の差を考えます。図で言うと\(\alpha－\beta\) です。
具体的な角度を入れるなら、例えば６０°－１５°＝４５°などを考えています。

その差をとった角度の正弦や余弦をどのように考えるのかというと、図のように点Ａから点Ｂまでの距離をもとの正弦と余弦で表し、さらに△ＡＯＢに余弦定理を使用するのです。この時、線分ＡＢの距離は三平方の定理で計算できます。

線分ＡＢの長さは三平方の定理で計算できます。

余弦定理で組み立てた式に三角比の公式 sin２θ＋cos２θ＝１ を適用すると、余弦に関する加法定理の関係式cos(Ａ－Ｂ)＝cosＡcosＢ－sinＡsinＢが得られるのです。

これはとりあえず０°～９０°の範囲の図形的な位置関係から関係式を導出するものですが、じつは三角関数として実数全体の範囲で一般の角度を考える場合でも、基本的な考え方は同じなのです。

  • ２つの角度の２つの三角形を作り、その角度の差によりもう１つの三角形を考える。
  • 三角形は、単位円周上の２点と原点で構成する。
  • 円周上の２点間の距離を三平方の定理で表し、さらに余弦定理を適用する。

この基本的な考え方のもとで証明をしていきます。
尚、その場合だと得られるのは余弦の「差」に関するcos (Ａ－Ｂ)の式になりますが、その式が証明されると変数の置き換えで残り３式も証明されるという形になります。

一般角の場合①　余弦 cos (Ａ－Ｂ)の式の証明

実数全体を範囲とする拡張された角度（一般角）でも加法定理が成立する事の証明は、一般的には次のように座標上の単位円周上の２点を考えて角度を統一的に扱います。

考え方自体は三角比の範囲の時と同じで、２点の「長さ」（プラスの値）を上手に使うのです。

まず単位円周上の２点（ｘ１,ｙ１）と（ｘ２,ｙ２）を考え、
これらの座標を（cosＡ,sinＡ）および（cosＢ,sinＢ）とおいてもよい事から始めます。
つまり(１,０)から２点まで測った角度をそれぞれＡおよびＢとしています。

このときの２点の位置関係は、ｘ座標で言うとどちらがどちらよりも大きくても（あるいは等しくても）構わず、むしろどちらの場合でも統一的に扱って証明の計算を進められる事がポイントです。

つまり、鋭角の場合・鈍角の場合・負の角度の場合・・といった場合分けをしなくてもよいという事です。

余弦の場合は、負の角度を代入しても同じ絶対値の正の角度を代入した時と同じ値である事【cos(－θ)＝cosθ】もポイントです。結論を言うと、加法定理のうち余弦の cos(Ａ－Ｂ)に着目するととうまくいくのです。

単位円周上の２点と原点で作られる三角形に注目します。この時に原点を頂点とする部分の角度はＡ－Ｂになります。（これは円周上の２点の位置関係によってプラスの値にもマイナスの値にもなります。）

この三角形に、余弦定理を適用します。余弦定理は辺の長さと１つの余弦に関して、実数全体の範囲の角度で正しい関係式を作ります。

★２点の座標をベクトルと考えて
「ベクトルの長さと内積は回転によって不変だから」・・という論法でやる事も可能です。

２点の長さの出し方は三角比の範囲の時と同じで三平方の定理を使います。（座標上の２点の距離の一般的な計算方法でもあります。）余弦定理で必要なのは２乗の形なので、長さを２乗した形は次のようになります。

(cosＡ－cosＢ)２＋(sinＡ－sinＢ)２
＝cos２Ａ＋cos２Ｂ－２cosＡcosＢ＋sin２Ａ＋sin２Ｂ－２sinＡsinＢ
＝２－２cosＡcosＢ－２sinＡsinＢ

【cos２Ａ＋sin２Ａ＝１、cos２Ｂ＋sin２Ｂ＝１なのでこのように式が簡単になります。】

他方、三角形の残りの２辺は単位円の半径ですから長さはともに１です。この条件のもとで余弦定理を考えてみると次のようになります。

(cosＡ－cosＢ)２＋(sinＡ－sinＢ)２＝１２＋１２－２・１・１・cos(Ａ－Ｂ)
⇔２－２cosＡcosＢ－２sinＡsinＢ＝１＋１－２cos(Ａ－Ｂ)
⇔ cos(Ａ－Ｂ)＝cosＡcosＢ＋sinＡsinＢ

【最後の式変形は両辺にある定数の「２」を消し、さらに両辺をー２で割り整理したものです。】

このように、加法定理のうち余弦の「差の形」のものが成立する事が分かります。この形は２乗の展開式に由来するものというわけです。また、角度の差をとる時に２つの項がプラスで結ばれる理由も証明の過程から比較的明確であるかと思います。２点間の距離の計算による２乗の展開式由来なので同符号というわけです。

この場合の角度には、三角関数の変数としての実数全体の範囲の任意の角度を代入しても成立します。これは余弦定理が実数全体の範囲で角度を代入した場合にも正しい関係式を作っているためです。円周上の２点と原点が同一直線上に並んで「三角形を作らない」場合にでも点同士の距離と余弦関数の値の正しい関係を表しています。

一般角の場合②　残り３式の導出

正弦と余弦に関する加法定理の残り３式はどのように導出するのかというと、それらはcos(Ａ－Ｂ)＝cosＡcosＢ＋sinＡsinＢをもとに出すのです。

まず、Ｂがプラスでマイナスであってもこの関係式は成立しますから、Ｂの部分を－Ｂに置き換えるとcos(Ａ＋Ｂ)＝cosＡcos(－Ｂ)＋sinＡsin(－Ｂ)＝cosＡcosＢ－sinＡsinＢとなります。

正弦のほうはどうするのかというと、ＢをＢ＋\(\pi\)／２に置き換えます。

cos(Ａ＋Ｂ＋\(\pi\)／２)＝cosＡcos(Ｂ＋\(\pi\)／２)－sinＡsin(Ｂ＋\(\pi\)／２)＝－cosＡsinＢ－sinＡcosＢ

他方で cos(Ａ＋Ｂ＋\(\pi\)／２)＝－sin(Ａ＋Ｂ) でもあるので、

－sin(Ａ＋Ｂ)＝－cosＡsinＢ－sinＡcosＢ⇔sin(Ａ＋Ｂ)＝sinＡcosＢ＋cosＡsinＢ

正弦の残り１式は、sin(Ａ＋Ｂ) のＢを－Ｂに置き換えて得ます。sin(Ａ＋Ｂ)＝sinＡcos(－Ｂ)＋cosＡsin(－Ｂ)＝sinＡcosＢ－cosＡsinＢ です。

これによって、正弦関数と余弦関数の加法定理４式が確かに成立する事になります。

参考までに、三角比の範囲の場合に cos(Ａ－Ｂ)のＢを－Ｂに置き換えてcos (Ａ＋Ｂ)にした場合の図形的意味は次図のようになります。これを一般化しているのが、三角関数で考えた一般の角度での加法定理です。単位円周上で考えれば、同様の図形的な位置関係を必ず作る事ができます。

三角比の範囲で考えた場合の cos(Ａ＋Ｂ)の図形的な解釈の１つです。三角関数の加法定理において角度部分を ｘ → －ｘ に置き換える操作は単に形式上そうできるというだけではなく、図形上の意味にも必ず対応しています。

具体例・応用例・覚え方

具体例についても見てみましょう。

例えば、９０°＝６０°＋３０°、９０°＝４５°＋４５°といった関係を加法定理は正しく表すでしょうか？

$$\sin\left(\frac{\pi}{3}+\frac{\pi}{6}\right)=\sin\left(\frac{\pi}{3}\right)\cos\left(\frac{\pi}{6}\right)+\cos\left(\frac{\pi}{3}\right)\sin\left(\frac{\pi}{6}\right)$$

$$=\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{1}{2}\cdot\frac{1}{2}=\frac{3}{4}+\frac{1}{4}=1$$

$$\sin\left(\frac{\pi}{3}+\frac{\pi}{6}\right)=\sin\left(\frac{\pi}{2}\right)=1 で一致します。$$

４５°のほうでやってみても同じで、

$$\sin\left(\frac{\pi}{4}+\frac{\pi}{4}\right)=\sin\left(\frac{\pi}{4}\right)\cos\left(\frac{\pi}{4}\right)+\cos\left(\frac{\pi}{4}\right)\sin\left(\frac{\pi}{4}\right)$$

$$=\frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}}=\frac{1}{2}+\frac{1}{2}=1$$

こういう形で成立するわけです。

１２０°－６０°＝６０°の場合を今度は余弦のほうでやってみると、

$$\cos\left(\frac{2\pi}{3}-\frac{\pi}{3}\right)=\cos\left(\frac{2\pi}{3}\right)\cos\left(\frac{\pi}{3}\right)+\sin\left(\frac{2\pi}{3}\right)\sin\left(\frac{\pi}{3}\right)$$

$$=-\frac{1}{2}\cdot \frac{1}{2}+\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{2}=-\frac{1}{4}+\frac{3}{4}=\frac{1}{2}=\cos\left(\frac{\pi}{3}\right)$$

加法定理が成立するなら、既知の三角関数の値を使って例えば４５°－３０°＝１５°といった半端な角度の正弦や余弦の値も分かるはずです。「１５°」における正弦の値を加法定理で計算すると次のようになります。

$$\sin\left(\frac{\pi}{12}\right)=\sin\left(\frac{\pi}{4}-\frac{\pi}{6}\right)=\sin\left(\frac{\pi}{4}\right)\cos\left(\frac{\pi}{6}\right)-\cos\left(\frac{\pi}{4}\right)\sin\left(\frac{\pi}{6}\right)$$

$$=\frac{1}{\sqrt{2}}\cdot\frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\cdot\frac{1}{2}=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4}$$

この計算値は約 0.2588 で、マクローリン展開で計算した値にほぼ一致します。

４５°＋４５°や６０°＋６０°のような場合は、より一般的にＡに対する２Ａとして「倍角の公式」の形にして捉える事も可能です。和積の公式や積和の公式も、加法定理の幾つかの式を組み合わせて変形したものです。

三角関数の微分公式の証明でも、加法定理を使用して計算を進めます。

加法定理の式の形の「覚え方」としては、複素数を利用する方法もあります。【これらは「説明」や「覚え方」としては有用ですが「証明」にはならないので注意。】

複素数の場合、指数関数表示（オイラーの公式）からｅｉ(θ＋φ)＝ｅｉθｅｉφですが、
cos(θ＋φ)＋ｉsin(θ＋φ)＝(cosθ＋ｉsinθ)(cosφ＋ｉsinφ)
＝cosθcosφ－sinθsinφ＋ｉ(sinθcosφ＋cosθsinφ)
を意味しますから、実部と虚部の値を比較すれば
cos(θ＋φ)＝cosθcosφ－sinθsinφ、sin(θ＋φ)＝sinθcosφ＋cosθsinφ
の関係が成立している事が分かります。
これらは三角関数の加法定理の内容そのものです。

（これはド・モアブルの定理で考えても同じです。
ただし、その定理の証明に加法定理が使用されているので、「加法定理の証明」としては
適切とは言えないのです。）

外積を使った証明

加法定理の別の証明方法として、３次元ベクトルの外積（ベクトル積、クロス積）を使う方法があります。

外積ベクトルは３次元のベクトルに対して考えるものですが、ｚ＝０としたｘｙ平面上の２つのベクトルに対して考える事は一応可能です。

そこで、次の２つのベクトルを考えます。
（角度θとφはプラスの値とします。ベクトルの大きさはどちらも１である事にも注意。）

$$\overrightarrow{a}=\cos\theta\hspace{2pt}\overrightarrow{e_1}+\sin\theta\hspace{2pt}\overrightarrow{e_2},\hspace{10pt}\overrightarrow{b}=\cos\phi\hspace{2pt}\overrightarrow{e_1}-\sin\phi\hspace{2pt}\overrightarrow{e_2}$$

$$\overrightarrow{e_1}=(1,0,0),\hspace{10pt}\overrightarrow{e_2}=(0,1,0),\hspace{10pt}（本当は\overrightarrow{e_3}=(0,0,1)もある。）$$

負の角度を使っても同じ事ですが、ここではプラスの値の角度の正弦にマイナス符号をつけた形で座標を表すとします。

そこで外積ベクトルを考えてみましょう。（外積について成立する公式を使用します。）

$$\overrightarrow{a}×\overrightarrow{b}=(\cos\theta\hspace{2pt}\overrightarrow{e_1}+\sin\theta\hspace{2pt}\overrightarrow{e_2})×(\cos\phi\hspace{2pt}\overrightarrow{e_1}-\sin\phi\hspace{2pt}\overrightarrow{e_2})$$

$$=-\cos\theta\sin\phi(\overrightarrow{e_1}×\overrightarrow{e_2})+\sin\theta\cos\phi(\overrightarrow{e_2}×\overrightarrow{e_1})$$

$$=-\cos\theta\sin\phi(\overrightarrow{e_1}×\overrightarrow{e_2})-\sin\theta\cos\phi(\overrightarrow{e_1}×\overrightarrow{e_2})$$

$$=-(\cos\theta\sin\phi+\sin\theta\cos\phi)(\overrightarrow{e_1}×\overrightarrow{e_2})$$

$$=(\cos\theta\sin\phi+\sin\theta\cos\phi)(-\overrightarrow{e_3})$$

他方で、この外積ベクトルは定義通りに考えれば向きは「ｚ軸のマイナス方向」であり、
大きさは\(|\overrightarrow{a}||\overrightarrow{b}|\sin(\theta+\phi)=\sin(\theta+\phi)\) です。

という事は、

$$\overrightarrow{a}×\overrightarrow{b}=\sin(\theta+\phi)\hspace{2pt}(-\overrightarrow{e_3})$$

という事でもありますから、２つの結果を等号で結べます。

$$(\cos\theta\sin\phi+\sin\theta\cos\phi)(-\overrightarrow{e_3})=\sin(\theta+\phi)(-\overrightarrow{e_3})$$

$$よって、\sin\theta\cos\phi+\cos\theta\sin\phi=\sin(\theta+\phi)【加法定理の証明終り】$$

この場合は、正弦の加法定理が直接示されています。（証明の最後の箇所では見やすいように項の順番だけ入れ替えています。）これを使って残りの３式も証明が可能です。

ここで行った計算は一体何なのかというと、前半で記した証明が三角形の「辺の長さ」を考えたのに対して、この外積を使った証明では平行四辺形の「面積」（三角形でも可能）を使ったという事です。本質的には、座標を使って証明するという同じ部類の２つの証明法と言えます。