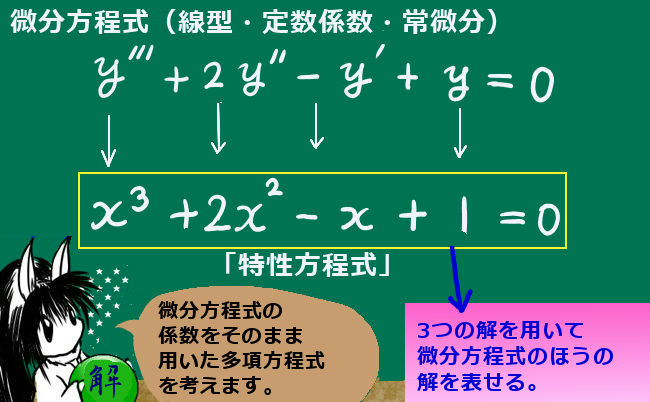
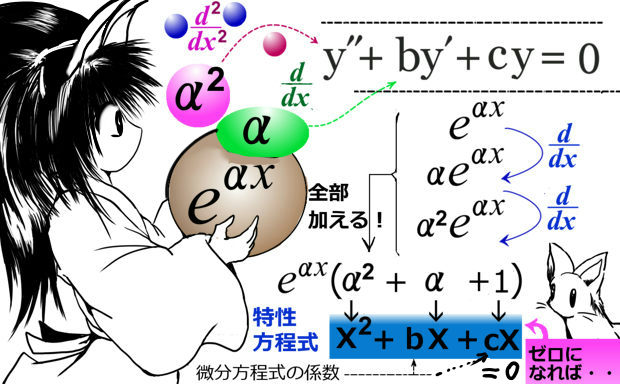
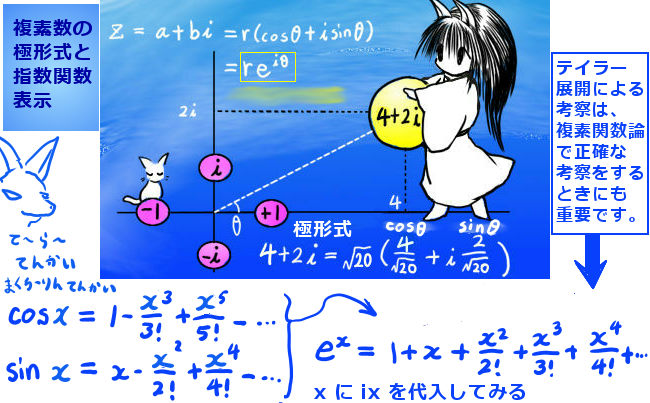
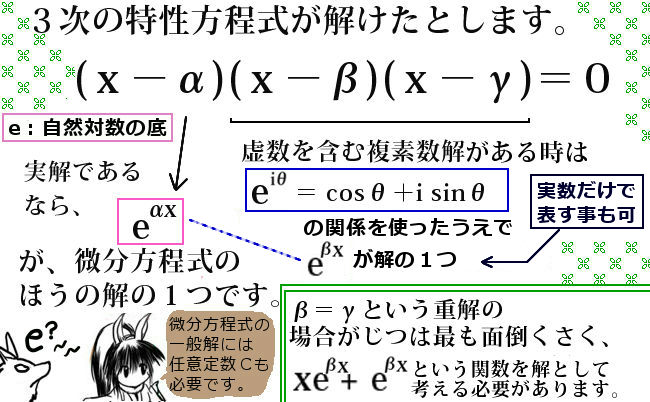
合成関数に関する偏微分の公式の物理での使用例を、ここでは1つ述べます。
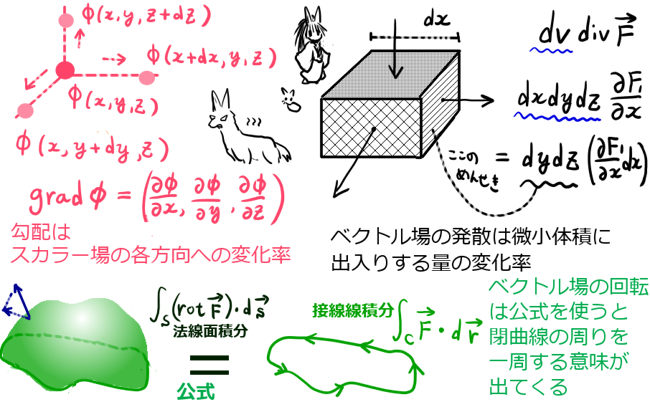
★ このページではベクトル解析で使用する「勾配」という考え方を使用します。
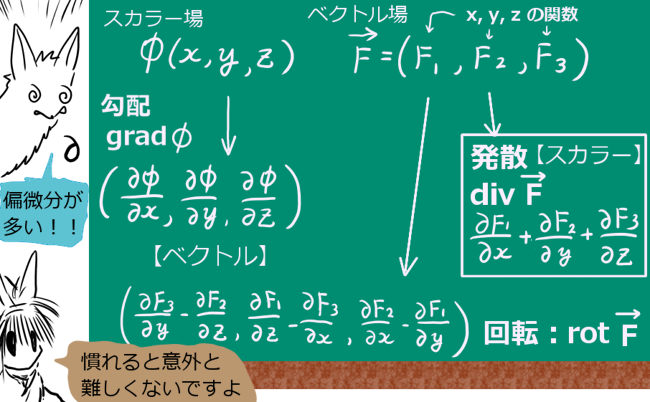
これは、多変数関数(多変数のスカラー関数)に対する偏微分によって表されるものです。
目次:
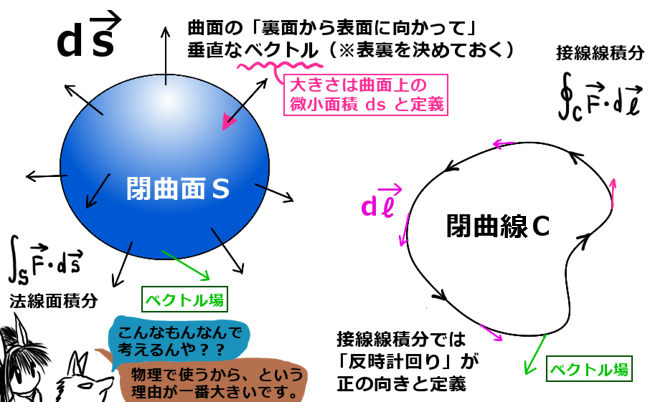
参考(サイト内リンク):接線線積分の定義と考え方
保存力の力ベクトルは、位置エネルギーの勾配ベクトルで表せる
先に結論の式を書きますと、力が「保存力」である場合に、位置エネルギーのxでの偏微分をx成分、yでの偏微分をy成分、zでの偏微分をz成分に持つベクトルは、保存力の力ベクトルに等しいという関係式があります。【※保存力で無い場合は成立しませんので注意。】
まず、「位置エネルギー」(あるいはポテンシャルエネルギー)U(x,y,z) を次のように定義します。これはベクトルでは無く、スカラー関数です。 $$\large U(x,y,z)=-\int_{\overrightarrow{R_O}}^{\overrightarrow{R}}\overrightarrow{F}(x,y,z)\cdot d\overrightarrow{r}$$ $$\large \mathrm{grad} U(x,y,z)=\left(\frac{\partial U}{\partial x},\frac{\partial U}{\partial y},\frac{\partial U}{\partial z}\right)$$ 力ベクトル F(x,y,z) が保存力である場合、次式が成立します:$$\large -\mathrm{grad} U(x,y,z)=\overrightarrow{F}(x,y,z) $$
★ プラスマイナスの符号の関係が、ちょっとごちゃごちゃするので注意。

この関係式は、古典力学の理論としては仕事とエネルギーの関係の話の延長線上にあります。
これは要するに数学的には、
「接線線積分の形の多変数関数の勾配ベクトルは、もとのベクトル関数と同じ形になる」
という事を言っています。通常の不定積分(あるいは積分区間に変数が入った定積分)は、通常の微分を考える事で元の関数に戻るという「微積分学の基本定理」がありました。それと似た形の式という事になります。
この関係式の証明のポイントは、合成関数の偏微分公式です。
ベクトルの内積の計算も直接的に関わります。
\(-\mathrm{gradU(x,y,z)}= \overrightarrow{F}(x,y,z)\) の証明
まず通常の微積分学の基本定理を用いたうえで、ベクトルの内積と合成関数の偏微分の公式をうまくかみ合わせます。
位置座標は全て「物体の位置」であるとして、位置座標に対応する時間成分tを考えます。
力ベクトルの成分についても同様に tの関数であると考えます。
$$\large \overrightarrow{F}(t)=(F_X(t),F_Y(t),F_Z(t))$$
$$\large 点\overrightarrow{R} での時刻をt、点\overrightarrow{R_O} での時刻を t_O とします。$$
Uの定義(力学での定義です)にマイナス符号があるので、
ここでは最初から「-U」を考えて、積分での表記をプラス符号で考えています。
★ 後述しますが、力が「保存力」であるという条件がないと、じつはまずこの式変形ができません。なぜかというと一般の接線線積分は、2つの端点だけでなく、その2点を結ぶ経路によって値が変わってしまうからです。力が保存力であるという条件は、この値が経路によらず一定の値であるとしてよいという条件です。
★ 古典力学の理論の中では、もともとは一般の力に対して時間で表したほうの式が先にあって、次に「保存力」という位置座標のみで決定するものを考えます。
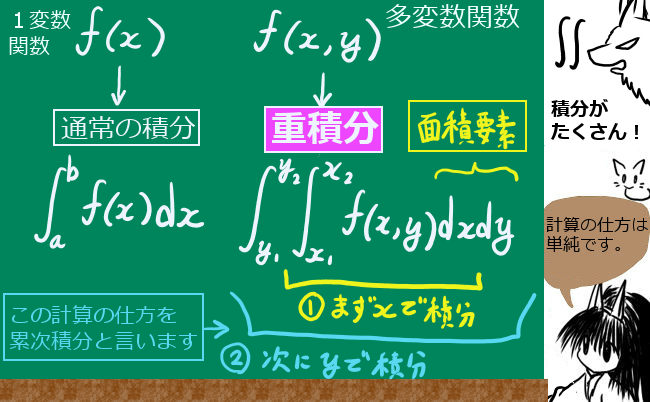
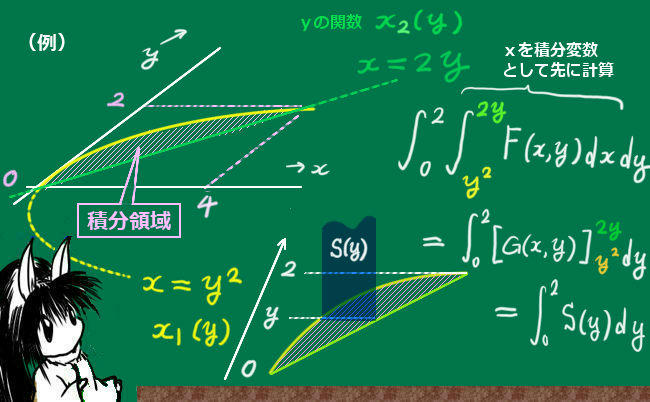
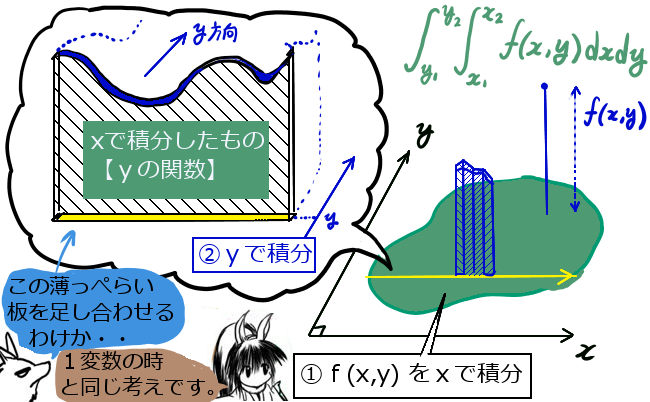
★ 積分区間にベクトルが入っている部分は、次の意味になります。 $$\large \int_{ \overrightarrow{R_O} }^{\overrightarrow{R}} \overrightarrow {F} (x,y,z) \cdot{d\overrightarrow{r}} $$ $$\large =\int_{x_O}^{x}F_X(x,y,z)dx+ \int_{y_O}^{y}F_Y(x,y,z)dy+ \int_{z_O}^{z}F_Z(x,y,z)dz $$ $$\large \overrightarrow {F}=(F_X,F_Y,F_Z),\hspace{10pt}\overrightarrow{R_O}=(x_O,y_O,z_O),\hspace{10pt}\overrightarrow{R}=(x,y,z)$$ dx の部分は x に関してだけ積分し、yやzは定数同様に扱います。つまり、偏微分と同じような考え方をするわけです。この場合の微積分学の基本定理は、積分と「偏微分」との関係になります。
次に、時間成分tで U(x,y,z) = U(x(t), y(t), z(t)) を微分します。
内積計算で3つの項の和にした部分は共通の積分変数tでの積分になっているので、通常の微積分学の基本定理がそのまま使えます。
この時、積分する対象として $$\large F_X(t) \frac{dx}{dt}$$ を1つの関数と捉える事がポイントです。
積分中の表記では$$\large {F_X( \tau ) \frac{dx}{d\tau}}$$ にしています。
$$\large\frac{dU}{dt}= \frac{d}{dt}\left(\int_{t_O}^{t}F_X( \tau ) \frac{dx}{d\tau} d \tau + \int_{t_O}^{t}F_Y( \tau ) \frac{dy}{d \tau } d \tau + \int_{t_O}^{t} F_Z( \tau ) \frac{dz}{d \tau } d \tau \right)$$
$$\large = F_X(t) \frac{dx}{dt} + F_Y(t) \frac{dy}{dt} + F_Z(t) \frac{dz}{dt}=\overrightarrow{F}(x,y,z)\cdot \frac{ d\overrightarrow {R}}{dt} $$
他方で、合成関数の偏微分公式を使うと U の時間微分の計算を別途に表現できるのです。
この場合、多変数 x、y、z が1つだけの変数tの合成関数になっているという事なので、表記としては$$\large \frac{\partial U}{\partial t}=\frac{dU}{dt}です。$$
ただし、もとの関数が U(x,y,z) という多変数関数なので、偏微分のほうの合成関数の微分公式を使う点に注意しましょう。
$$\large \frac{\partial U}{\partial t}=\frac{dU}{dt}= \frac{\partial U}{\partial x} \frac{\partial x}{\partial t}+ \frac{\partial U}{\partial y} \frac{\partial y}{\partial t} + \frac{\partial U}{\partial z} \frac{\partial z}{\partial t} $$ $$\large = \frac{\partial U}{\partial x} \frac{dx}{dt}+ \frac{\partial U}{\partial y} \frac{dy}{dt} + \frac{\partial U}{\partial z} \frac{dz}{dt} =(\mathrm{gradU})\cdot \left( \frac{ d\overrightarrow {R}}{dt}\right) $$
最後の結果は「Uの勾配ベクトル」と「速度ベクトル」との内積です。
内積はスカラーであり、勾配はスカラー関数をベクトルの関数変換する演算である事を意識すると分かりやすいと思います。
同じものを2通りの数式で表せる事になるので、等号で結ぶ事ができます。
これによって、次の関係式が成立する事になります。
$$\large – \overrightarrow{F}(x,y,z)\cdot \frac{ d\overrightarrow {R}}{dt} = \mathrm{gradU}\cdot \frac{ d\overrightarrow {R}}{dt} $$
$$これは、\overrightarrow{A}\cdot \overrightarrow {C} = \overrightarrow{B}\cdot \overrightarrow {C} という関係になっています。 $$
これが証明の根拠になるわけですが、数学的には
\(\overrightarrow{A}\cdot \overrightarrow {C} = \overrightarrow{B}\cdot \overrightarrow {C} \) から直ちに\(\overrightarrow{A}= \overrightarrow{B}\) とは言えない事には注意しましょう。
そうならない場合もあるのです。
しかし、この場合は \(\overrightarrow {R}\) が特定の座標点では無くて「任意の座標点」です。
特定の点だけではなく、どんな座標の点を考えたとしてもこの関係式は成り立つ、という意味です。
ですから、\(\overrightarrow {R}\) に対して内積をとると等しい値になる2つのベクトル\(– \overrightarrow{F}(x,y,z)と\mathrm{gradU(x,y,z)}\) は、全く同じ関数でなければならないのです。
$$ つまり 、- \overrightarrow{F}(x,y,z)\cdot \frac{ d\overrightarrow {R}}{dt} = \mathrm{gradU}\cdot \frac{ d\overrightarrow {R}}{dt} かつ 「\overrightarrow {R} は任意の(実)ベクトル」なので、$$
$$-\overrightarrow{F}(x,y,z)=\mathrm{gradU}(x,y,z)\Leftrightarrow -\mathrm{gradU}(x,y,z)= \overrightarrow{F}(x,y,z) という事です。【証明終り】$$
「保存力」の物理的な意味
保存力とは力がなす仕事が経路に依存せず、始点と終点の位置だけに依存する力を言います。これは結構強い条件が課されている事になりますが、万有引力、重力(地表面での万有引力を近似したもの)、ばねの力、クーロン力などは保存力になるので、物理の理論の中では結構使い物になります。
逆に、保存力でない力の簡単な例は摩擦力などです。
一般の力ベクトルに対しては、少しだけ上述でも触れましたが、
次の形の時間変数による積分が先にあります。
$$\large T(t)-T(t_O)=\int_{t_O}^{t} \overrightarrow {F} (\tau) \cdot \frac{d \overrightarrow{r} }{d\tau}d\tau$$
ここで、1変数の通常の積分であれば積分変数をtからxに変換できます。
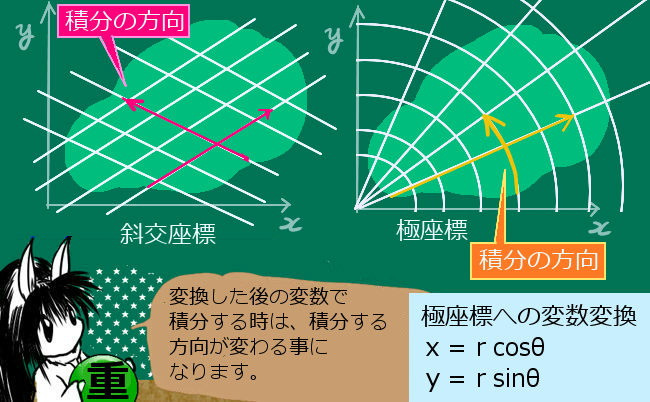
しかし、この場合は「接線線積分」なので、経路は1通りでは無く様々なものがあるのです。
経路によって値が異なりますから、同じ値の定積分になるという意味での積分変数の変換は無条件にはできない・・という事です。
ベクトルに対する一般の接線線積分の場合、値が始点と終点だけでは決定しないので次のように表記します:
$$一般の接線線積分の表記:\int_C \overrightarrow {F} \cdot d \overrightarrow {r}\hspace{10pt}Cは特定の関数で表される経路 $$
ここで、経路によらず「経路の始点と終点だけをしていれば値が定まる」という条件をつけると、もちろん数学的な扱いは簡単になります。
そのような条件がつけられた種類の力が保存力であり、上記のように具体的に当てはまる力も存在するというわけです。
保存力がなす仕事の値(仕事量)は始点と終点の位置だけで決まります。これを「位置エネルギー」あるいは「ポテンシャルエネルギー」などと呼びます。
これは運動エネルギーに対する用語です。位置エネルギーと運動エネルギーの合計を、力学的エネルギーと呼びます。
尚、保存力ではない摩擦力などの力に対しては、位置エネルギーは考えないのです。
これを数学的に取り扱った場合、上述いたしましたように、合成関数に対する偏微分の公式などが重要な役割を担っているというわけです。