微分積分学・解析学 | 理数系学習サイト　kori

積分の考え方と基本計算

恭平

微分が「傾き」を表すのに対し、積分は「面積」を表すというのが基本的な考え方です。
（使い方は色々あって、「体積」を表す事もできます。また、後述するように通常の図形問題で言う面積との相違点もあります。）

考え方と計算方法
具体的な計算例
定積分は「負の値」やゼロの事もある

英：積分 integral　定積分 definite integral

考え方と計算方法

関数ｙ＝ｆ(ｘ)の微分係数はｘの各点ごとに１つ、傾きの値として決まります。これに対して、積分の場合にはｘの２点を指定するごとに面積の値として決まります。この２点で挟まれる閉区間は積分区間と呼ばれます。この面積は、ｆ(ｘ)を表す曲線とｘ軸、指定した２点を通りｘ軸に垂直な直線で囲まれる面積です。

積分の計算には微分演算の逆算を使用します。そのため、基本計算でも微分の知識が必要です。

この面積の計算が積分で、このように定まった積分区間内の面積の値は特に「定積分」と呼ばれます。
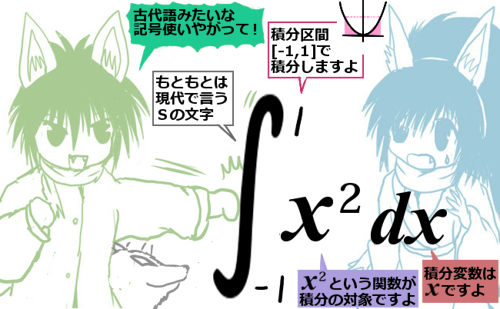
積分区間 [ａ,ｂ] における関数ｙ＝ｆ(ｘ)に対する定積分は、記号では次のように書きます。

定積分の記号の書き方と意味

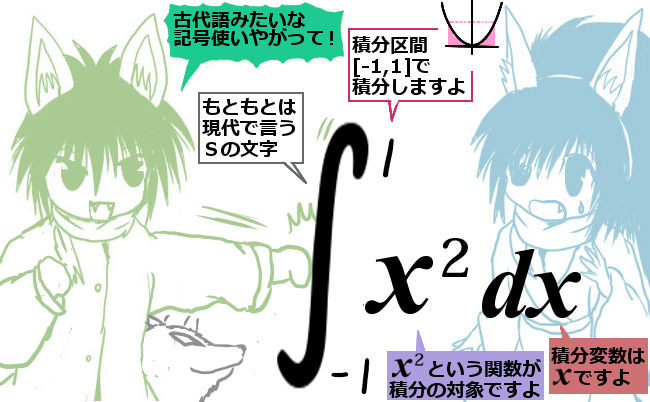
「定積分」を次のように書きます。この計算をする事を「積分する」とも言います。$$\large{\int_a^bf(x)dx}$$

$\int$ の記号はＳの文字由来と言われる。（「和」「合計」を表す語の頭文字）
上下に添えられた文字は積分区間 [ａ,ｂ] の事
ｄｘは対象の関数の変数がｘである事を表す。
【ｄｘと書く由来は微小な区間の幅ｄｘをｆ(ｘ)に乗じて合計し面積を近似しているため】

定積分の値は１であるとか２であるとか、何らかの「値」になります。
（ｆ(ｘ)が負であれば定積分の値は負の数になる事もあり、０でもあり得ます。）

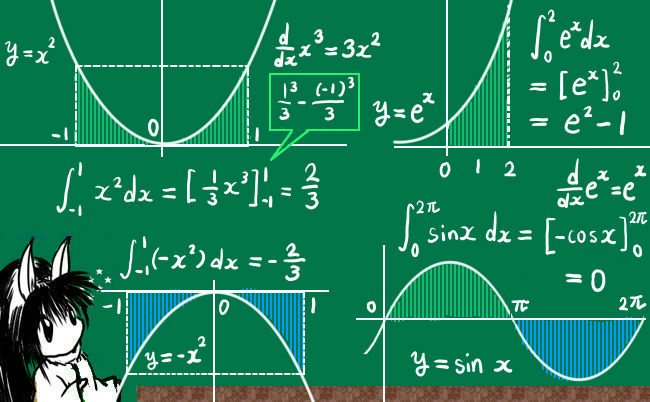
ｆ(ｘ)に具体的な関数を入れて、特定の積分区間の定積分を考えます。$$\int_{-1}^1x^2dx\hspace{15pt}\int_{0}^2e^xdx\hspace{15pt}\int_{0}^{\large{\pi}}\cos xdx\hspace{15pt}\int_{1}^{\large{e}}\ln xdx$$

次に、具体的にどういう計算をすればよいかという話になります。
結論を先に言うと次の手順で定積分は計算できます。

定積分の計算の手順

微分すると「対象の関数ｆ(x)になる」別の関数Ｆ(x) を探す。
【例えばｆ(ｘ)＝ｘ^２であればＦ(ｘ)＝ｘ^３／３,　ｆ(ｘ)＝cosｘであればＦ(ｘ)＝sinｘ】
積分区間 [ａ,ｂ] のａ、ｂをＦ(ｘ)に代入したものを用意する。
【例えば積分区間 [０,１]でＦ(ｘ)＝ｘ^３／３であればＦ(０)＝０とＦ(１)＝１／３を用意】
Ｆ(ｂ)－Ｆ(ａ)を計算する。これが積分区間 [ａ,ｂ] でのｆ(ｘ)の定積分の値になる。
【例えばＦ(１)－Ｆ(０)＝１／３－０＝１／３になる。】 $$\left(この計算の時に、F(b)-F(a)を\left[F(x)\right]_a^bとよく書きます。\right)$$

「微分するとｆ(x)になる」別の関数Ｆ(x)の事を、原始関数とも言います。
このように計算できる事は、微積分学の基本定理がもとになっています。

基本的な考え方としては、ｘ軸とｙ軸、ｘ軸上の１点 (ｘ,０) に垂直な直線とｙ＝ｆ(ｘ) の曲線で囲まれる面積をＳ(ｘ)として、微分の定義式に当てはめるとＳ(ｘ)を微分して得られる導関数(ｄ／ｄｘ)Ｓ(ｘ)＝ｆ(ｘ) となるというものです。これはｙ軸、すなわちｘ＝０から始めているので、Ｓ(ｂ)からＳ(ａ)を差し引けば閉区間 [ａ,ｂ] における面積となるという事です。

ある点での微分操作により導関数を計算する時には関数自体はどこから始まってもよく、図の面積Ｓ(ｘ)も微分する計算を考えるだけならどこから始まってる面積でもよい事になります。しかしそれでは実際の値としての面積を計算できないので、定積分を微分操作からの逆算で計算する時にはＳ(ｘ)－Ｓ(ａ)のように考えて値を出します。

この時、微分方程式を解く時の注意点にも共通しますが、ある関数Ｆ(ｘ)を微分してｆ(ｘ)になる時、定数ｃを加えたＦ(ｘ)＋ｃという関数も同様に「微分するとｆ(ｘ)になる」関数になります。定積分を計算する時にＦ(ｂ)－Ｆ(ａ)という引き算を考えるのは、その不定の定数を除去して面積の値を確定させるという工夫です。

具体的な計算例

ｙ＝ｘ^２の積分区間 [－１,１] での定積分は次のように計算します。

$$\int_{-1}^1x^2dx=\left[\frac{1}{3}x^3\right]_{-1}^1=\frac{1}{3}-\frac{-1}{3}=\frac{2}{3}$$

この計算では、１／３という係数がくっつけて【ｘ^３を微分すると３ｘ^２なので３で割る】、最後の引き算を考える時に―１をｘ^３／３に代入し、それをさらに「引き算する」ので符号はプラスになり、結果的に２つの正の数の値を加える形になっています。

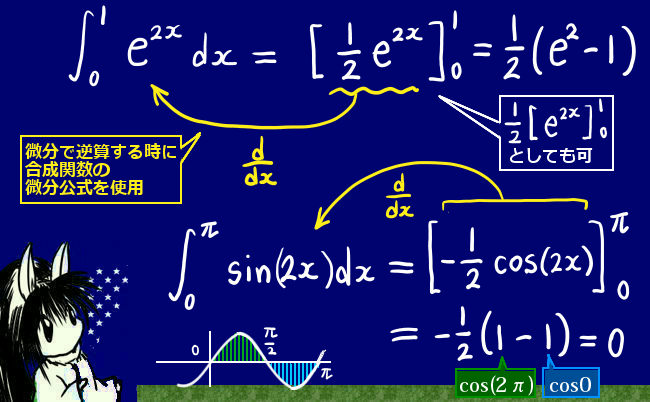
$$\int_{0}^2e^xdx=\left[\large{e^x}\right]_0^2=e^2-1$$

$$\int_{0}^{\large{2\pi}}\sin xdx=-\left[\large{\cos x}\right]_0^{\large{2\pi}}=-(1-1)=0$$

微分すると sinｘになる関数は－cosｘですが、ここでは符号の煩雑さを避けるために積分区間の端点（$2\pi$ と０）を代入するところでカッコの外にマイナス符号を出しています。このような操作は、符号も含めて定数倍に関しては一般的に行う事ができる操作です。

なお、この定積分の計算を１次関数（図形的には直線）に適用すると、きちんと「三角形の面積公式」で計算した時と同じ結果を得ます。

$$\int_0^3xdx=\frac{1}{2}[3x^2]_0^1=\frac{3}{2}(1-0)=\frac{3}{2}$$

$$底辺×高さ÷２で計算して\hspace{5pt}\frac{1\cdot 3}{2}=\frac{3}{2}\hspace{5pt}でも同じ$$

グラフがある点を境にｙ軸に関して対称であったり、点対称になっている場合には図形的な性質を利用して計算を簡単にできる場合もあります。

個々の関数に関してどのように定積分を計算するかは結局のところ微分の問題になる事も多く、合成関数の微分などを使用する事もあります。三角関数の場合には加法定理などを使って工夫してから定積分を計算すると分かりやすい事もあります。

$$\int_0^1e^{2x}=\left[\frac{1}{2}e^{2x}\right]_0^1=\frac{1}{2}\left(e^2-1\right)$$

$$\int_0^{\pi}(\cos x\sin x)dx=\frac{1}{2}\int_0^{\pi}\sin (2x)dx=-\frac{1}{4}\left[\cos (2x)\right]_0^{\pi}=-\frac{1}{4}(1-1)=0$$

$$\int_{1}^{\large{e}}\ln xdx=\int_{1}^{\large{e}}\left[x\ln x-x\right]_{1}^{\large{e}}=(e\ln e-e)-(1\cdot 0-1)=(e-e)-(-1)=1 $$

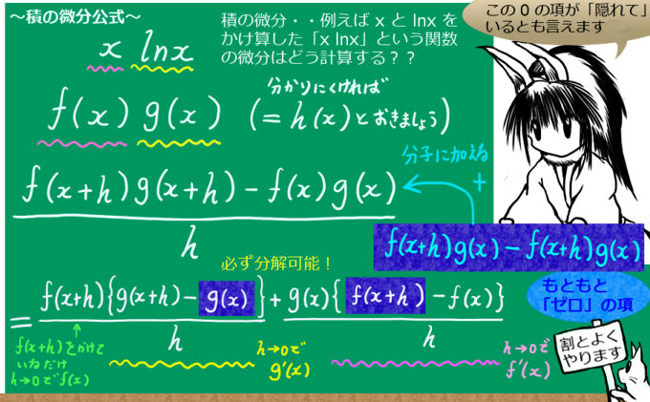
【(d／dx)(ｘlnｘ－ｘ)＝lnｘ＋ｘ／ｘ－１＝lnｘ＋１－１＝lnｘ　積の微分公式使用】

ｙ軸に関して対称な関数（偶関数）の定積分を [－ａ,ａ] で考える時は[０,ａ]での定積分の２倍の値を考えればよく、原点に対して点対称な関数（奇関数）の定積分を [－ａ,ａ] で考える場合は値は必ず０になります。
上記の例でも、積分区間が[－ａ,ａ]の形であれば偶関数・奇関数の性質を使って計算できるものもあります。

定積分は「負の値」やゼロの事もある

関数が負の値になる時も、定積分はそのまま計算するルールになっています。

ｙ＝－ｘ^２のような関数を積分区間 [－１,１] で積分する時は、定積分の結果は負の値になります。

$$\int_{-1}^1(-x^2)dx=\left[-\frac{1}{3}x^3\right]_{-1}^1=-\frac{1}{3}-\left(-\frac{-1}{3}\right)=-\frac{2}{3}$$

こういうとき、マイナス符号の扱いが煩雑になりがちなので、計算しやすいように工夫したほうがよい事もあります。例えばこの場合には「ｙ＝ｘ^２の同じ積分区間での定積分にマイナス符号をつければよい」事になるので、次のようにも書けます。

$$\int_{-1}^1(-x^2)dx=-\int_{-1}^1x^2dx=-\left[\frac{1}{3}x^3\right]_{-1}^1=-\left(\frac{1}{3}-\frac{-1}{3}\right)=-\frac{2}{3}$$

ｙ＝sinｘの[０,$2\pi$] での定積分は０ですが、これは０から$\pi$までの定積分の値がプラスで、そこから定積分はマイナスに転じます。それで、差し引きゼロになってしまうという事です。

$$\int_{0}^{\large{\pi} }\sin xdx=-\left[\large{\cos x}\right]_0^{\large{\pi}}=-(-1-1)=2\hspace{15pt}\int_{\large{\pi}}^{\large{2\pi} }\sin xdx=-\left[\large{\cos x}\right]_{\large{\pi}}^{\large{2\pi} }=-(1+1)=-2\hspace{15pt}$$

半周期の範囲で正弦関数とｘ軸で囲まれる面積がぴったりと整数になるのは意外かもしれませんが、とりあえず積分の計算によるとそういう結果になるという事です。

プラスとマイナスの両方の値を取り得るという意味では、定積分の計算は平面幾何での図形の「面積」と少し違っている事になります。
もし平面幾何の意味での「面積」の総和を出す必要があるなら、確実に計算するのであればｙ＝ｆ(ｘ)が合った時には絶対値記号をつけて|ｙ|＝|ｆ(ｘ)|の定積分を計算します。つまり、負の部分は全てｘ軸に関してひっくり返して計算する事になります。
他に、関数の２乗を考える場合など、関数の値が確実にプラスである事が確定している時には定積分の計算結果は引かれている部分が無い「面積」の総和になります。

複素数の指数関数表示【オイラーの式】

恭平

複素数の指数関数表示について説明します。

これは「オイラーの公式」とか「オイラーの式」とも呼ばれますが、じつは同じ名前・似た名前で全く別の公式や定理が複数存在します。大変紛らわしく、使用する都度に「複素数に関する・・」「実関数の解析学における・・」「幾何学での・・」このように断り書きをつけるのは大変不便なので、
このサイトではｅ^ｉθを表す語としては「複素数の指数関数表示」という表現を採用します。

複素数の指数関数表示とは次のようなものです。

複素数の指数関数表示

複素数の極形式表示を指数関数の形で書く事ができ、次のように定義します。 $$e^{i\theta}=\cos\theta +i\sin\theta$$ このｅは自然対数の底です。ｅ^ｉθを exp(ｉθ)と書く事もあります。これは実数範囲の指数関数での表現と同じです。(exponential の略)

こういう形なので、ｅ^ｉθの絶対値は１になります。

$$|e^{i\theta}|=|\cos\theta +i\sin\theta|=1$$

さて、このように「指数関数」で書くからには指数関数としての規則を満たしているのかというと、きちんと満たしています。これらの性質、特に微分の演算は表記を簡易にするので便利です。

成立する演算

積の演算：ｅ^ｉθｅ^ｉω＝ｅ^ｉ(θ＋ω)
ｅ^ｉθｅ^ｉω＝(cosθ＋ｉsinθ)(cosω＋ｉsinω)
＝cos(θ＋ω)＋ｉsin(θ＋ω)　【ドモアブルの定理より】
＝ｅ^ｉ(θ＋ω)
微分：(d／dθ)ｅ^ｉθ＝ｉｅ^ｉθ 【合成関数の微分使用】
(d／dθ)ｅ^ｉθ＝(d／dθ)(cosθ＋ｉsinθ)
＝－sinθ＋ｉcosθ＝ｉ(cosθ＋ｉsinθ)
＝ｉｅ^ｉθ

見ての通り、この指数関数表示は三角関数の性質に直接的に関わるものです。
（ドモアブルの定理の成立根拠は三角関数の加法定理。）

実際、一見唐突にも見えるこの「指数関数の定義域の拡張」は三角関数をもとに考えられたものです。

「三角関数と指数関数では全然違うではないか？」という話ですが、それらをテイラー展開すると似た形をしているのです。（微分の性質も似ている事に注意：ｅの指数関数は微分に関して１回周期、三角関数は４回周期でもとの関数に戻ります。さらに正弦関数と余弦関数は微分により符号を変えながら互いに互いの導関数に変化します。）

特にマクローリン展開（ｘ＝０でのテイラー展開）の形にすると形は似てきます。

$$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots$$

$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$$

$$\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots$$

ここで、正弦関数の場合は「偶数項」が抜けていますが、余弦関数を見るとちょうどそれを補うように項が並んでいるのです。（正弦関数を微分すると余弦関数になる事に対応します。）これを合わせると、ちょうど指数関数のほうで使っている項が並ぶ事になります。

しかしそれでも符号が変わっている箇所は対応しないという話になりますが、ここで指数関数ｅ^ｘに「ｉｘ」を「形式的に」代入してみるという工夫をしてみます。

$$e^{ix}=1+ix-\frac{x^2}{2!}-i\frac{x^3}{3!}+\frac{x^4}{4!}+i\frac{x^5}{5!}-\frac{x^6}{6!}+\cdots$$

これをよく注意して見ると、次の規則があります。

虚数単位ｉは奇数項にのみつき、偶数項にはつかない。
奇数項と偶数項に分けてみると、それぞれが１項ごとにプラスマイナスの符号が反転する。

そこで、奇数項と偶数項に分けて式を整理すると次のようになります。

$$e^{ix}=\left(1+\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\cdots\right)+i\left(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots\right)$$

$$=\cos x +i\sin x $$

このように「導出」できるわけですが、基本的には複素数の指数関数表示は上記のように「定義」するものになります。複素数の範囲に定義域を拡張する時には上記のようにすると定義するわけです。

しかしそういう事を言うと、定義域の拡張の際に「別のやり方」もあるのではないかという問題も起きます。上記のように定義する必然性がないのではないか、という事にもなります。

この件について複素関数論においては、「正則関数」になるように定義域を拡張する場合には上記のようにｅ^ｉθ＝cosθ＋ｉsinθ のようにするしかない、という位置付けになります。（その際にも重要になるのはじつはテイラー展開です。）

逆関数の微分公式【計算例と証明】

恭平

逆関数の微分公式の内容、具体例、証明について述べます。

公式の内容
具体例と計算例
公式の証明

y = 2x のとき、両辺を２で割って x = y / 2 とも書けます。
このように、y = ｙ(x) のとき、逆に x = ｘ(y) と書けるとき、ｘ(y) をｙ(x) の逆関数と呼びます。
【この時の関数の記号はｆでもＦでも何であっても問題ありません。】

高校数学の中で重要な例としては、指数関数と対数関数を挙げる事ができます。
これらは、互いに逆関数同士の関係にあるのです。

y=x² のような場合に逆関数を考えると x=$\pm \sqrt{y}$のように x を y で表した関数が２つ出てきてしまうので、「１つの変数に対して１つの値が定まる」という関数の定義に反し、ちょっとした面倒事が起きます。
こういう場合には x の定義域と y の値域を特定の区間に定めれば逆関数を書けるという形になります。
逆関数の定義に関するそういった細かい事は多くあるのですが、ここでは本質ではないので略します。

高校数学で覚える必要はありませんが三角関数の逆関数を「逆三角関数」と言い、
sin x に対して arcsin x（「アークサイン x」）と書きます。
この逆三角関数は一見使いづらい関数なのですが、
その微分の性質から、一部の微積分の計算（例えばテイラー展開や不定積分の計算）で有用な働きをする事があります。この逆三角関数を微分する時には、逆関数の微分公式を使用します。

公式の内容

逆関数を考えた時、もとの関数を微分して得られる導関数と、逆関数を微分して得られる導関数の間にはある関係式が必ず成立するというのが、逆関数の微分公式です。内容は、次のようになります。

逆関数の微分公式

ｙ＝ｙ(x)の時にｘ＝ｘ(ｙ)と表せる時、次の関係式が成立します。 $$\frac{dy}{dx}={\large\frac{1}{\frac{dx}{dy}}}$$ ここで左辺はｘの関数で、具体的な計算においては右辺はｙの関数ですが、ｙはｘで表せるという前提なので右辺もｘだけの関数として表す事ができます。（※ただし後述するように具体的な計算ではｙをｘに直す作業が面倒である事があります。）
もちろん、分母は０になってはいけないという前提はあります。

ちょっと一見よく分からない公式だと思うかもしれませんが、ｘをｙで表した時に「ｘをｙで微分して得られる導関数」の逆数が、もとのｙをｘで微分して得られる導関数に必ず等しくなるという関係式です。

式としては単純で互いに逆数であるという関係ですから、ｄｘ／ｄｙ＝・・の形として見ても公式は成立します。つまり基本的には公式を次のように書き換える事もできます。

$$\frac{dx}{dy}={\large\frac{1}{\frac{dy}{dx}}}$$

これは、具体例で見たほうが分かりやすいと思います。

このような逆関数の導関数を考える時、もとの関数の導関数との間に常に成り立つ関係式があります。

具体例と計算例

具体的に公式を使うための手順は次のようになります。
もとの関数ｙ＝ｙ(ｘ)の導関数を計算したい場合であるとします。

関数と逆関数を、y=y(x),　x=x(y) の形で出しておく。
逆関数のほうについて、導関数を計算する。【※これが簡単にできる場合でないと、公式を使う意味があまりない事になります。】$$\frac{dx}{dy}を計算$$
得られた逆関数の導関数（ｙの関数）を、逆関数の微分公式に代入します。$$\frac{dy}{dx}={\large \frac{1}{\frac{dx}{dy}}}\hspace{5pt}に\hspace{5pt}\frac{dx}{dy}\hspace{5pt}を入れる$$
この段階で得られる計算結果は「y の関数」の形になっているので、y=y(x)を代入して x の関数にすれば、
それが y に対して x で微分したｄｙ／ｄｘの正しい形になっています。 $$式の変数をｘだけにすれば\hspace{5pt}\frac{dy}{dx}\hspace{5pt}の結果になる$$

※合成関数でもこの「y を x の関数の形に戻す」作業がありますが、一般には y = f(x) を代入すればよいというものでした。しかし、逆関数の微分の場合は、この作業について少し工夫がいる場合があります。

具体的な計算例を次に記します。
ここでは参考までに、逆三角関数の微分の計算も記してあります【高校では不要】。

逆関数の微分の具体例

逆関数の微分公式は、通常の微分計算で多く使うというよりは、特定の微分公式を導出するために使われる事が多いように思います。

１次関数の例：y＝２,　x＝y／２の時、 $$\frac{dx}{dy}=\frac{1}{2}\hspace{5pt}により、$$ $$\frac{dy}{dx}={\large\frac{1}{\frac{dx}{dy}}}={\large\frac{1}{\frac{1}{2}}}=2$$ この場合には直接微分しても、あるいはグラフを見ても分かる結果ではありますが、逆関数の微分公式も確かに成立しているという事です。
２次関数の例：ｘ＞０かつｙ＝$\sqrt{x}$, ｘ＝ｙ² の時、 $$\frac{dx}{dy}=2y\hspace{5pt}により、$$ $$\frac{dy}{dx}={\large\frac{1}{\frac{dx}{dy}}}= \frac{1}{2y} =\frac{1}{2\sqrt{x}}$$ ここでは平方根のほうの導関数を計算するために、２次関数を逆関数とみなしています。
もちろん、この計算はｙを直接ｘで微分しても同じ結果です。
指数関数と対数関数の例：y＝e^x, x＝ln y の時、 $$\frac{d}{dx}e^x={\large\frac{1}{\frac{d}{dy}\ln y}}={\large\frac{1}{\frac{1}{y}}}=y=e^x$$ 指数関数と対数関数の微分公式は一見全く異なる形であるようにも見えますが、じつはこうしたつながりもあるというわけです。
逆三角関数と三角関数の例：ｙ＝ arcsin x, ｘ＝ sin y の時、$$\frac{d}{dx}\arcsin x={\large\frac{1}{\frac{d}{dy}\sin y}}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-\sin^2y}}=\frac{1}{\sqrt{1-x^2}}$$ ここでは「逆三角関数の導関数」を知るために、通常の三角関数を逆関数とみなしています。
計算過程では sin²x+cos²x=1 の関係を使用しています。
余弦の逆三角関数の例：y＝arccos x, x＝cos y の時、$$\frac{d}{dx}\arccos x={\large\frac{1}{\frac{d}{dy}\cos y}}=\frac{1}{-\sin y}=\frac{-1}{\sqrt{1-\cos^2y}}=\frac{-1}{\sqrt{1-x^2}}$$
正接の逆三角関数の例：y＝arctan x, x＝tan y の時、 $$\frac{d}{dy}\tan y==\frac{1}{\LARGE{\frac{1}{\cos^2y}}}\hspace{5pt}により、$$ $$\frac{d}{dx}\arctan x={\large\frac{1}{\frac{d}{dy}\tan y}}=\cos^2y=\frac{1}{1+\tan^2y}=\frac{1}{1+x^2}$$

高校数学では、指数関数と対数関数の関係あたりを逆関数の関係で結べる事を理解していれば、基本的にはじゅうぶんかと思います。

逆三角関数の微分 — 【逆関数の微分公式：arcsin x の導関数の導出の例：】arcsin xの微分を、「sin xの微分公式」と「逆関数の微分公式」から導出する手順です。x = sin y の時に「y を変数とする形」で逆関数の微分を出すのは、じつはかなり簡単です。（公式により y で微分し分母に入れるのみ。）
ただ、そのあとで y を x の関数の形にうまく戻すために、工夫が必要な事があるのです。

※逆三角関数の別の表記方法

あくまで表記方法の問題なのですが、逆三角関数を sin^-1xとも書きます。
もちろんその場合は(sin x)^-1=１／(sin x) とは全く異なる関数・・なのです。
個人的にこれは紛らわしい表記だとも思うので、このサイトでは arcsin x などの表記を使用します。

公式の証明

y=Y(x), x=X(y) として、まず Δｘ = X(y+k)－X(y) とすると
k → 0 の時に Δx → 0 となります。（その逆である「Δｘ→ 0 の時 k → 0 」も成立）

X(y+k)－X(y) について Δx という文字でおいたのは、ここでは X(y+k)－X(y) というものが「ｘの変化」に等しいという事を見やすくするためです。別に他の文字でも支障はありません。

これを上手に利用すると、同じ極限が２通りの方法で表せます。その２通りの方法による結果がｄｙ／ｄｘと１／（ｄｘ／ｄｙ）であり、それゆえに両者を等号で結べるというのが証明の内容です。
その点で、合成関数の微分公式のように１本の式だけで証明できない点が少しだけ異なります。

ここで、微分の定義の式を書きます。

$$\frac{dy}{dx}={\large\lim_{\Delta x \to 0}\frac{Y(x+\Delta x)-Y(x)}{\Delta x}}$$
これは定義通りの式です。しかし、極限をとる変数としてΔｘを使っているところに計算上の工夫があります。ここの極限をとる変数は、h でなくとも何でも成立します。

上記の微分を表す微分を計算すると、次のようにも表せます。

$$ {\large\lim_{\Delta x \to 0}\frac{Y(x+\Delta x)-Y(x)}{\Delta x} } =\lim_{k \to 0}{\large\frac{Y(X(y)+X(y+k)-X(y))-Y(X(y))}{\Delta x}}$$
$$ ={\large\lim_{k \to 0}\frac{Y(X(y+k))-Y(X(y))} {\Delta x}} ={\large\lim_{k \to 0}{\large\frac{y+k-y}{\Delta x} }} ={\large\lim_{k \to 0}\frac{k}{\Delta x} }={\large\lim_{k \to 0}\frac{1}{\frac{\Delta x}{k}} }$$
$$ ={\large\lim_{k \to 0}\frac{1}{\frac{X(y+k)-X(y)}{k}} } ={\Large\frac{1} {\frac{dX(y)}{dy}}}={\Large\frac{1}{\frac{dx}{dy}} }$$

最初の変形では、分子のところだけΔｘをもとの形Δx = X(y+k)-X(y)に直してしまい、
ｘをｘ＝Ｘ(y)で書く事により、ｘ＋Δｘ＝X(y+k)としています。

次に、関数を y 変数になるように整理し、Δx→0 の時 k→0 なので k の極限にしています。

そのあとで、少しややこしいのですが逆関数の重要な性質「Ｙ(Ｘ(y))＝Ｙ(x)＝y 」（Ｘ(y)＝ｘに注意）を使って、Ｘ(Ｙ(y+k)) = y + k としています。
その後の計算は、例えば２／３＝１÷（３／２）＝１／（３／２）などと、同じ計算です。

これらの結果から、
$$\lim_{\Delta x \to 0}{\large\frac{Y(x+\Delta x)-Y(x)}{\Delta x}}=\frac{dy}{dx}={\Large\frac{1}{\frac{dx}{dy}} }【証明終り】$$

逆関数の性質 — Ｘ(ｙ)＝ｘに y＝Ｙ(ｘ) を代入してＸ(Ｙ(ｘ))＝ｘとしても同じです。

サイト内関連記事【高校数学の微積分】

積の微分公式と商の微分公式

恭平

積の微分公式と、それの変形版である商の微分公式の内容、具体例、証明について述べます。
（英：product rule, quotient rule）
これは関数同士の「掛け算」「割り算」の形になっている関数を微分する時に成立する公式です。

公式の内容
計算の具体例
公式の証明

積と商の形の関数は統一的に捉える事ができるので同時に記します。
詳しくは後述していますが、商の場合にはｆ(ｘ)と１／ｇ(ｘ)の「積」と捉えればよいので基本的には同じ形の公式なのです。

公式の内容

ｙ＝ｘｅ^ｘといった関数同士の「積」の形になったものを微分する時には積の微分公式が使えます。
また、正弦関数を「x で割った」(sin x)／x などには商の微分公式が使えます。

関数ｆ(ｘ)とｇ(ｘ)の積ｆ(ｘ)ｇ(ｘ)、商ｆ(ｘ)／ｇ(ｘ)　を微分した時には次の公式が成立します。
ここで、ｆ(ｘ)とｇ(ｘ)をｆ、ｇと記しています。

積と商の微分公式

$$積の微分公式：(fg)^{\prime}=f^{\prime}g+fg^{\prime} \hspace{20pt}商の積分公式\left(\frac{f}{g}\right)^{\prime}=\frac{f^{\prime}g-fg^{\prime}}{g^2}$$ これらは本質的には全く異なる公式ではなく、同種類のものであると捉えたほうがよいでしょう。

商の微分については、分母にあるのは「『微分してない g(x)』の２乗」です。

積の微分公式については、２つの項は足し算なので順番はどっちでもよいのですが、
「ｆ’ｇ +ｆｇ’」の順番にしたほうが、商の微分公式との関係で「覚えやすい」かとは思います。

計算の具体例

公式を使って計算する手順としては、f(x) と g(x) のそれぞれについて「x で微分した関数」と、「微分してない（もともとの）関数」をパーツとして用意し、公式に当てはめて丁寧に計算するというものになります。

まず、積の微分公式の具体的な計算の例をいくつか見てみます。

積の微分公式を使った計算例

ｙ＝sinx cosx 【２つの三角関数の積】の微分は次のようになります。$$\frac{d}{dx}\{(\sin x)(\cos x)\} =(\sin x)^{\prime}(\cos x)+(\sin x)(\cos x)^{\prime} =\cos^2x-\sin^2x$$
加法定理を考えると、この結果はcos 2x に等しくなります。sin x cos x=(sin 2x)／2 として、ｘで微分した時の結果と一致します。（この時、合成関数の微分公式を使用しているので注意。）
ｙ＝sin^２x の微分を考えます。
これに積の微分公式を適用する場合にはｙ＝(sin x)・(sin x)と考えるわけです。$$\frac{d}{dx}\{(\sin x)(\sin x)\} =(\sin x)^{\prime}(\sin x)+(\sin x)(\sin x)^{\prime} =2\cos x\sin x$$
これは sin 2x と表す事もできます。
また、sin²x を合成関数の微分公式で微分した結果と一致します。
さらに、加法定理・半角の公式でsin^２x＝（１－cos２ｘ）／２と変形してからｘで微分しても同じ結果です。
ｙ＝ｘe^ｘ【ｘと指数関数の積、ｅは自然対数の底】を微分すると次のようになります。 $$\frac{d}{dx}(xe^x)=(x)^{\prime}e^x+x(e^x)^{\prime}=e^x+xe^x=e^x(1+x)$$ 微分公式 (e^ｘ)’ ＝ e^ｘを使っています。
ｙ＝ｘlnｘ【ｘと、ｅを底とする対数関数の積】の微分を考えます。 $$\frac{d}{dx}x\ln x=(x)^{\prime}\ln x + x(\ln x)^{\prime}=1\cdot \ln x + x\cdot \frac{1}{x}= \ln x + 1$$ これを変形して両辺を積分すると、対数関数についての積分のほうの公式が得られます。$$\ln x = \left(\frac{d}{dx}x\ln x \right) – 1 なので、$$ $$\int \ln x dx=x\ln x -x+C が得られます。$$
積分のほうの「部分積分」の公式は、積の微分公式を変形して
$$f^{\prime}g=(fg)^{\prime}-fg^{\prime}$$の両辺を積分したものです。
ｆ(ｘ)・{g(ｘ)}^－１を、合成関数の微分公式も使って積の微分公式に適用すると商の微分公式が得られます。これについてはこのページで後述する証明の箇所でより詳しく説明します。

２番目の例のように微分の計算方法がいくつかあって、積の微分公式を使う事はその方法の１つであるというパターンもあります。計算結果が合っていればどの方法でも構いません。（入試を受験する場合にはなるべく効率のよい計算方法を考えたり、複数の方法で微分する事で計算結果のチェックをするようにしたほうがいいと思います。）

これらの中で、具体的な関数の微分計算も大事である場合もあるのですが、特に積分のほうの部分積分の公式を得るために使われるという事は覚えておくと便利かもしれません。

続いて、商の微分公式の具体的な計算例です。

商の微分公式を使った計算例

ｙ＝(sin ｘ)／ｘを微分すると次のようになります。 $${\large\frac{d}{dx}\frac{\sin x}{x} =\frac{ (\sin x)^{\prime}x-(x)^{\prime}(\sin x) }{x^2} =\frac{x\cos x-\sin x}{x^2} }$$
ｙ＝(ln ｘ)／ｘを微分すると次のようになります。 $${\large\frac{d}{dx}\frac{\ln x}{x} =\frac{(\ln x)^{\prime}x-(x)^{\prime}\ln x}{x^2} =\frac{x\frac{1}{x}-\ln x}{x^2}=\frac{1-\ln x}{x^2} }$$
正接関数 tan x の微分公式は、じつは商の微分公式により導出されます。$$\tan x=\frac{\sin x}{\cos x}なので、$$ $$\frac{d}{dx}\tan x=\frac{(\sin x)^{\prime}(\cos x)-(\sin x)(\cos x)^{\prime}}{\cos^2x}=\frac{\cos^2x +\sin^2x}{\cos^2x}=\frac{1}{\cos^2x} $$sin x と cos x の微分公式を用いて丁寧に計算すれば証明できます。
三角比の公式 sin^２ｘ＋cos^２ｘ＝１を使用しています。
三角関数のマイナー組である余接 (cos x)／(sin x)、正割 1／(cos x)、余割 1／(sin x) 【高校ではこれらを覚える必要なし】の微分公式も、商の微分公式を用いれば証明できます。
具体的な計算例として、余接関数を微分すると次のようになります。$$\frac{d}{dx}\cot x=\frac{d}{dx}\frac{\cos x}{\sin x}=\frac{(\cos x)^{\prime}\sin x-\cos x(\sin x)^{\prime}}{\sin^2x}=\frac{\sin^2 x+\cos^2 x}{\sin^2x}=\frac{1}{\sin^2x}$$
正割のように 1／g(x) の形の場合、f(x) = 1 ですから、f'(x) = 0 であり、公式の項が１つ消えるので計算は簡単になります。
一般的に、 1／g(x) の形の関数の微分は次のようになります。 $$\left(\frac{1}{g}\right)^{\prime}=\frac{0\cdot g-1\cdot g^{\prime}}{g^2}=\frac{g^{\prime}}{g^2}$$これは公式として新たに暗記する必要はありません。
むしろ、商の微分公式でこのような式もすぐに導出できるようにしておくとよいでしょう。

これらの具体例を見てみると積と商の微分公式は、初等関数の微積分という範囲に限って見ると割と重要な公式である事が、何となくつかめるのではないかと思います。

公式の証明

証明の方法は合成関数の微分公式や逆関数の証明方法と大体考え方は似ています。積や商の微分公式の場合、証明は合成関数や逆関数と比較すると比較的容易です。

結論を言うと「隠れている『０』」を加えたりしてあげる事で証明できます。

■ 積の微分公式の証明　■ 商の微分公式の証明
■ 片方の公式からもう片方の公式を導出するやり方

積の微分公式の証明

積の微分公式の場合、 f(x+h)g(x) － f(x+h)g(x) という「隠れている項」を考える事で、２つの導関数の和の形を作れます。この考え方自体は、数学の他のところ（大学数学も含め）でも、割とよく使われます。

$$\frac{d}{dx}(f(x)g(x))={\large \lim_{h \to 0}\frac{f(x+h)g(x+h)-f(x)g(x)}{h}}$$
$$={\large\lim_{h \to 0}\frac{f(x+h)g(x+h)-f(x+h)g(x)+f(x+h)g(x)-f(x)g(x)}{h} }$$
$$ ={\large\lim_{h \to 0}f(x+h)\frac{g(x+h)-g(x)}{h} }+\lim_{h \to 0}g(x){\large\frac{f(x+h)-f(x)g(x)}{h} }$$
$$ =f(x){\large\frac{dg}{dx} }+g(x){\large\frac{df}{dx}}=f(x)g^{\prime}(x)+f^{\prime}(x)g(x) =f^{\prime}g+fg^{\prime}【証明終り】$$

証明の最後のところは、f(x)をf と略して和の順番を変えて整理しただけになります。

「隠れている『０』」の項を分子の部分に加えてあげる事で証明できます。積の微分公式の場合、
f(x+h)g(x) － f(x+h)g(x) ＝０という項を加える事で「２つの導関数の和」の形を必ず作る事が可能です。

商の微分公式の証明

商の微分公式も同様の方法で証明できます。

まず分母のg(x+h)とg(x)を通分します。
その後で「-f(x)g(x)+f(x)g(x) (=0)」を分子に加えるという、積の微分公式同様の考え方をします。

$$\frac{d}{dx}\frac{f(x)}{g(x)}={\large\lim_{h \to 0}\left(\frac{f(x+h)}{g(x+h)}-\frac{f(x)}{g(x)}\right)\cdot\frac{1}{h}}$$

$$={\large\lim_{h \to 0}\frac{f(x+h)g(x)-f(x)g(x+h)}{h\cdot g(x)g(x+h)} }$$

$$ ={\large\lim_{h \to 0}\frac{f(x+h)g(x)-f(x)g(x)+f(x)g(x)-f(x)g(x+h)}{h\cdot g(x)g(x+h)} }$$
$$ ={\large\lim_{h \to 0}g(x)\frac{f(x+h)-f(x)}{h\cdot g(x)g(x+h)}}-{\large\lim_{h \to 0}f(x)\frac{g(x+h)-g(x)}{h\cdot g(x)g(x+h)} }$$

$$ ={\largeg(x)\frac{df}{dx}\frac{1}{(g(x))^2}-f(x)\frac{dg}{dx}\frac{1}{(g(x))^2}}$$

$$= {\large\left(\frac{df}{dx}g(x)-f(x)\frac{dg}{dx}\right)\frac{1}{(g(x))^2} = \frac{f^{\prime}g-fg^{\prime}}{g^2}}【証明終り】$$

計算の途中にある分母のところにあるｇ(ｘ＋ｈ)は、ｈ→０でｇ(ｘ)になるので、これともう１つのｇ(ｘ)と合わせて公式の分母の２乗を作るわけです。

片方の公式からもう片方の公式を導出するやり方

さて、このように積の微分公式と商の微分公式は、独立に証明できるわけです。

では、片方の公式からもう片方を導出できるでしょうか？

積の公式のほうに１／ｇ(ｘ)としてみると、これは(ｇ(ｘ))^－１と考える事ができますから、合成関数のほうの微分公式を使えるのです。計算してみると次のようになります。

$$\frac{d}{dx}\frac{1}{g(x)}=\frac{d}{dx}(g(x))^{-1}=-\frac{dg}{dx}\cdot\frac{1}{(g(x))^2}$$

「ｇ(ｘ)の２乗」というものとマイナス符号が合成関数の微分のほうから出てくるわけで、これを積の微分公式に当てはめると商の微分公式になります。

商の微分公式の第１項はｇ(ｘ)を「約分」する事もできるわけですが、こちらの証明方法の観点だともともとの１／ｇ(ｘ)の形に由来するというわけです。

他方、商の微分公式のほうが先に証明されているとしましょう。この時に、簡単に前述しましたが１／ｇ(ｘ)の導関数が今度は合成関数の考え方を使わずに、商の微分公式から導出できるわけです。もちろん結果は同じです。

そのうえで、商の微分公式の中のｇ(ｘ)を、１／ｇ(ｘ)に置き換えます。ちょっとややこしいですが、微分の部分も含めて丁寧に代入して整理すると積の微分公式になるのです。

つまり積の微分公式と商の微分公式は、独立に証明もできるし、互いに片方の公式からもう片方を導出する事も可能であるわけです。

こういった、証明の方法が複数あるという事については別に知らなくても支障はないし、大学入試の受験という観点からも証明自体が出題される頻度はかなり低いと思いますが、いくつかの方法で試してみる事は計算の練習にはなると思います。

サイト内関連記事【高校数学の微積分】

合成関数の微分公式【計算例と証明】

恭平

合成関数の微分公式の内容、具体例、証明について記します。
（英：chain rule）

公式の内容
具体的な計算例
公式の証明

■微分の定義と公式は別途に詳しくまとめています。

公式の内容

合成関数の微分公式は、ｆ(ｘ)＝ｆ(ｙ(ｘ))の形、つまり合成関数の形である時に次のように表されます。

合成関数の微分公式

$$\frac{df}{dx}=\frac{df}{dy}\frac{dy}{dx}$$ 形としてはあたかも「ｄｙ」が分母分子で「約分される」かのような形となっている事が特徴です。これは覚えるコツでもありますが、数学的にも間接的に意味のある形（例えば証明の仕方との関連）になっています。

これはどういう事かというと、次のような手順を踏めば微分ができるという事です。

ｆ(ｘ)＝ｆ(ｙ(ｘ)) でｙ＝ｙ(ｘ)とおき、
ｆ(ｘ)＝ｆ(ｙ(ｘ)) ＝ｆ(ｙ)のように、ｙが変数であるかのような形にする。
ｆ(ｙ) をｙが変数であるとみなしｙで微分する。これがｄｆ／ｄｙ
ｙ＝ｙ(ｘ)を微分する。これがｄｙ／ｄｘ
ｄｆ／ｄｙとｄｙ／ｄｘを掛け算する。
（この段階では見かけ上の変数としてｘとｙが混在しています。）
ｙ＝ｙ(ｘ)を代入して式の変数をｘだけにする。これがｆ(ｘ)＝ｆ((ｙ(ｘ))をｘによって微分して得る導関数に一致する。

合成関数とは、例えばｆ(ｘ) ＝ (２ｘ＋３)^２のような形の関数の事で、ｙ(ｘ)＝２ｘ＋３のようにおいてｆ(ｙ(ｘ)) ＝(ｙ(ｘ))^２という構造になっています。

これを微分する時に、ｆ(ｘ) ＝ (２ｘ＋３)^２であれば式を展開してから普通にｘで微分する事もできますが、ｙ(ｘ)＝２ｘ＋３のｘによる微分と組み合わせて計算できる事もできるというのが合成関数の微分公式です。しかも、その組み合わせ方は「掛け算」するだけでよいというのがこの公式の意味です。

★ｙ＝ｙ(ｘ)と実際におくのは丁寧に計算する場合で、この置き換えが簡単な式である場合には頭の中で計算をしてしまう事もできます。
例えばｆ(ｘ) ＝ (２ｘ＋３)^２のような関数であれば、
ｙという文字を使わずに「(２ｘ＋３)という塊とその２乗」で考えるという事です。

下図のように f(x) = cos(ωx) 【例えば cos 2x】のように表される関数の他に、$$e^{2x},\hspace{10pt}\sin^2x(=(\sin x)^2)\hspace{10pt}\frac{1}{1-x},\hspace{10pt}\sqrt{1-x^2}\hspace{10pt}$$なども、みな合成関数の仲間達です。
これらを微分する時には、普通の微分公式をそのままでは適用できない場合があります。そのようなものについては「合成関数の微分公式」で微分をして導関数を計算します。

【合成関数の微分公式】この図では、cos(ωx) という形の「合成関数」を例にして考えています。余弦関数の cos の中に、ωｘという別の関数が入っていて「合成」されているので、このような形の関数を合成関数と言います。見ての通り、微分をすると、cos が -sin になるだけでなく、ωというオマケがくっついてきます。この形の関数は、物理でもよく使いますので重要だと思います。物理では、「時間（秒）」を変数として、角速度ω[rad/s]を用いて cos(ωt), sin(ωt)といった関数を考えたりします。

具体的な計算例

この微分公式を使った計算は理論・応用ともに重要なのですが初見では計算の仕方が紛らわしく理解しにくい面もあるので、ここでは具体例についてかなり詳しく挙げておきます。

ｆ(ｘ) ＝ (２ｘ＋３)^２の微分を合成関数の微分公式で計算する場合は次のようにします。

ｙ(ｘ)＝２ｘ＋３とおき、ｙをｘで微分して得る導関数ｄｙ／ｄｘ＝２と、ｙを変数とみなしたｆ(ｙ)＝ｙ^２をｙで微分して得る導関数ｄｆ／ｄｙ＝２ｙ＝２(２ｘ＋３)を用意します。これらを掛け算します。

すると、ｄｆ／ｄｘ＝(ｄｆ／ｄｙ)・(ｄｙ／ｄｘ)＝２・２(２ｘ＋３)＝８ｘ＋１２です。

ｆ(ｘ) ＝ (２ｘ＋３)^２＝４ｘ^２＋１２ｘ＋９のように式展開して直接ｘで微分すると、ｄｆ／ｄｘ＝８ｘ＋１２となります。この結果は、合成関数の微分公式を使った場合の結果と確かに一致しています。

他の合成関数の場合の微分についても見てみましょう。特に重要度が高いのは（大学入試だけでなくその後についても）、三角関数（および三角比）や指数関数が合成関数の形になっている場合です。

三角関数の合成関数：f(x) = cos(2x)

cos(ωx) という形の関数の、さらにより具体的な関数として、
f(x) = cos(2x)という「2x」という形が余弦関数に入っている場合の微分計算を、例として手順を追って見てみましょう。
f(x) = cos(2x) = sin y の「x による微分」は、合成関数の微分公式を利用して計算できるのです。

cos(2x)の 2x を y とおき、cos y を「y で」微分します。
公式により、これは -sin y になります。
$$\frac{d}{dy}\cos y=-\sin y$$
次に、y = 2x を x で微分します。
これは、一次関数x の微分「１」に定数２をかければよいので２になります。
$$\frac{d}{dy}(2x)=2$$
ｄｆ／ｄｙとｄｙ／ｄｘの積をつくります。
これは、本当に「掛け算するだけ」の計算です。
$$\frac{df}{dy}\frac{dy}{dx}=(-\sin y)\cdot 2 =-2\sin y$$
・・最後に、y に y = 2x を代入し、x だけの式にします。それがf(x)を x で微分して得られる導関数に等しいわけです。
$$\frac{df}{dx}=\frac{df}{dy}\frac{dy}{dx}=-2\sin y=-2\sin (2x)$$

このタイプの微分は、イラストでも触れていますように、じつは物理でもよく使う微分計算です。
慣れてくると、cos(２ｘ) のような形である時点で微積分する時には「２」を忘れてはいけないという事にすぐに気付くようになるでしょう。

次に、指数関数が合成関数になっている場合です。考え方は上記と同じになります。
ここでは特に自然対数の底の指数関数を扱います。理論上も応用上もその場合が特に重要です。

指数関数の合成関数：ｆ(ｘ) = e^(2x)

ｆ(ｘ) = e^(2x)は、指数関数の変数が「2x」などになった形の合成関数です。
このタイプも、微分方程式の解法などを含めて物理学で比較的よく使う微分計算だと思います。

2x = y とおきます。
元の関数をｙで表すと、f(x)=e^2x=e^y(=f(y))です。

y を x で微分します。$$\frac{dy}{dx}=\frac{d}{dx}(2x)=2$$※少し慣れれば、このへんは暗算でやってしまうくらいになると思います。
f(y)を y で微分します。$$\frac{df}{dy}=\frac{d}{dy}e^y=e^y$$これは、e の指数関数の微分公式そのままですね。
合成関数の微分公式を適用します。
ここでは、y を x の形に直すところまで一緒にやってしまいます。 $$\frac{d}{dx}e^{2x}=\frac{df}{dy}\frac{dy}{dx}=2\cdot e^y=2e^{2x}$$

この計算方法を見ると、一般に次のように、 $$「定数 a に対して、\frac{d}{dx}e^{ax}=ae^{ax}」$$ という事が言える事も、分かるかと思います。
f(x) = e^2x の 2x が、3x でもあっても ax であっても、計算方法は同じだからです。
もっとも、これを新しく公式として「暗記」する必要は、ありません。
必要なのはあくまで普通の指数関数の微分公式と、合成関数の微分公式なのです。

注意点としては、ｙ＝ｙ(ｘ)の置き換えをした時には、最後に y を x の形に直す必要がある（場合が多い）という事だと思いますが、忘れさえしなければ数学でも物理でも、難しい計算は少ないと思います。

前述の通り、簡単な合成関数であれば置き換えは頭の中だけでやってしまっても支障ありません。

三角関数の合成関数で、少し紛らわしいタイプのものを挙げておきます。

三角関数の合成関数：ｆ(ｘ) = sin²x

三角関数を「２乗した」sin²x などの場合です。
この場合は、 sin x = y と考えて、元の関数が $f(y)=y^2$であると考えるのです。
従いまして、微分の計算は次のようになります。

まず合成関数の微分公式に必要な材料を計算します。
$$\frac{df}{dy}=\frac{d}{dy}y^2=2y,\hspace{10pt}\frac{dy}{dx}=\frac{d}{dx}\sin x=\frac{dy}{dx}\cos x $$
２つの材料を、掛け合わせてできあがりです。
$$\frac{d}{dx}\sin^2x=\frac{df}{dy}\frac{dy}{dx}=2y\cos x=2\sin x \cos x = \sin 2x$$

（ここで sin 2x は、sin(2x) の事です。）
他方、sin 2x の微分は 2cos(2x) になります。（上の例のcos 2x と同様の手順です。）
sin² x　の微分とは、少々違った結果になる事が分かるかと思います。
一見、「似てるっぽい？」かもしれませんが、計算方法を間違えないようにしたい例のひとつであるわけです。
尚、最後の結果が「x の半角」の正弦の形になる事は、三角関数の半角の公式を導出する手順で使う式（加法定理由来）を使って$$\sin^2 x=\frac{1-\cos 2x}{2}である事から、$$ $$\frac{d}{dx}\frac{1-\cos 2x}{2}=\frac{2\sin 2x}{2}=\sin 2x$$となる事と調和しています。
また、この例の微分は積の形の微分公式で計算する事も可能で、同じ結果を得ます。

他に、うっかりすると合成関数である事を見落としがちなタイプのものを挙げます。

合成関数になっている反比例関数：f(x) = １／(１－ｘ)

$$続いて、f(x)=\frac{1}{1-x}という関数の微分を考えてみましょう。$$ これも、合成関数として微分する必要があるのです。
「これのどこが合成関数？」かと思われるかもしれませんが、分母の 1-x を y と考えて合成関数と見る必要があるのです。この y = 1 – x の微分においては、定数の「１」は微分すると０になって消えます。

再び、材料作りです。
$$\frac{df}{dy}=\frac{d}{dy}\frac{1}{y}=\frac{d}{dy}y^{-1}=-y^{-2},\hspace{10pt}\frac{dy}{dx}=\frac{d}{dx}(1-x)=-1 $$
合成関数なので掛け合わせます。
$$\frac{d}{dx}\frac{1}{1-x}=\frac{df}{dy}\frac{dy}{dx}=(-1)(-y^{-2})=y^{-2}=\frac{1}{(1-x)^2}$$

この例の微分計算は単項式の微分公式さえ知っていれば難しくはありませんが、
「うっかり合成関数である事を見落とすと」符号を間違えてしまう例と言えます。
「マイナス１乗」の微分で１つマイナス符号がつきますが、この例では合成関数の部分に―ｘの項があるのでさらにもう１つマイナスがつき、結果はプラスになるわけです。
似たような関数でも、$$\frac{d}{dx}\frac{1}{1+x} の場合だと$$ $$\frac{d}{dx}(1+x)=1ですから、$$ $$\frac{d}{dx}\frac{1}{1+x}=-(1+x)^{-2}=-\frac{1}{(1+x)^2}$$となり、こちらはマイナスの符号がつくわけです。符号の違いは、ｘの増加に対して関数が増加するか減少するかに対応しています。

平方根がかかっている形の関数も、「１／２乗」という事ですから合成関数の形になります。

平方根を含む合成関数：$f(x)=\sqrt{1-x^2}$

例として、$$f(x)=\sqrt{1-x^2}$$という関数の場合は、1-x² = y として微分計算をします。
この関数は、図形で言うと原点を中心とした半径１の円の「第１象限」の部分を関数として表したものです。

前の例と同じように材料をまず作りますが、今回再び丁寧に、２つに分けます。
まず、かんたんなほうからです。
$$\frac{dy}{dx}=\frac{d}{dx}(1-x^2)=-2x$$
同じく材料として、「y の平方根」の形の関数の微分を計算します。
これは単項式の微分公式で「a=1/2」の場合を使えばいいのですが、少し分かりにくいかもしれません。
$$\frac{df}{dy}=\frac{d}{dy}\sqrt{y}=\frac{d}{dy}y^{\frac{1}{2}}=\frac{1}{2}y^{-\frac{1}{2}}=\frac{1}{2}\frac{1}{\sqrt{y}}$$
２つの材料がそろえば、あとは掛け合わせて、ｙを x の関数の形に戻すだけです。
$$\frac{d}{dx}\sqrt{1-x^2}=\frac{df}{dy}\frac{dy}{dx}=(-2x)\frac{1}{2}y^{-\frac{1}{2}}=\frac{-x}{\sqrt{y}}=\frac{-x}{\sqrt{1-x^2}}$$

この例で用いている「平方根の微分」は慣れないと、とっつきにくい場合も多いかと思います。
ただ、このタイプの関数の微分は物理でもよく使いますので、知っておくと便利です。

物理や工学等の理論でこれらの関数の微積分を使用するには「これは合成関数の形だから・・」という説明は省略して結果だけ書く事が普通ですので、その意味でも計算の仕方に慣れておく事は大事かと思います。計算に慣れれば簡単な合成関数であれば「公式」としての形を特に暗記しようと努めなくても自然に計算できるようになります。

公式の証明

合成関数の微分公式の証明は次のようにします。

f(ｘ) = ｆ(ｙ(ｘ)) 、ｙ = ｙ(ｘ) である時、まず次のように考えます。

ｆ(ｙ(ｘ))の導関数を、定義の極限を含む形で書きます。
ｆの中の変数部分ｙ(ｘ＋ｈ)について、ｙ(ｘ＋ｈ)＝ｙ(ｘ＋ｈ)－ｙ(ｘ)＋ｙ(ｘ)と変形します。

$$\frac{d}{dx}f(x)=\lim_{h \to 0}\frac{f(y(x+h))-f(y(x))}{h}=\lim_{h \to 0}\frac{f(y(x+h)-y(x)+y(x))-f(y(x))}{h} $$

次に、ｙ(ｘ＋ｈ)－ｙ(ｘ)という項を「掛けて割る」操作をします。これは値としては「１」を掛ける操作なので自由に行ってよいのです。

$$ \frac{d}{dx}f(x)=\lim_{h \to 0}\frac{f(y(x+h)-y(x)+y(x))-f(y(x))}{h}\cdot \frac{y(x+h)-y(x)}{y(x+h)-y(x)}$$

$$=\lim_{h \to 0}\frac{f(y(x+h)-y(x)+y(x))-f(y(x))}{y(x+h)-y(x)}\cdot\frac{y(x+h)-y(x)}{h}$$

ここで、ｚ＝ｙ(ｘ＋ｈ)－ｙ(ｘ)とおきます。そのようにおかなくても証明できますが、見やすくするという意味です。ｚに置き換わる部分は３つあり、ｄｆ／ｄｘは次のような形になります。

$$\frac{d}{dx}f(x)=\lim_{h \to 0}\frac{f(z+y(x))-f(y(x))}{z}\cdot\frac{z}{h}$$

ここで、ｈ→０のとき、lim_ｈ→０ｚ＝lim_ｈ→０（ｙ(ｘ＋ｈ)－ｙ(ｘ)）＝ｙ(ｘ)－ｙ(ｘ)
＝０ですから、ｈとｚの両方を０に近づけるという意味で「lim_{ｈ,ｚ→０} 」と書く事ができます。このときに、

$$\lim_{h \to 0}\frac{z}{h}=\lim_{h \to 0}\frac{y(x+h)-y(x)}{h}=\frac{dy}{dx}$$

である事に注意し、ｙ＝ｙ(ｘ) を変数とみなしてｙと書くと次のようになります。

$$\frac{d}{dx}f(x)=\lim_{h,z \to 0}\frac{f(z+y)-f(y)}{z}\cdot\frac{z}{h} =\frac{df}{dy}\frac{dy}{dx}【証明終り】$$

このように、１つの導関数を別の導関数の積で表せるという結果になるのです。

２項定理

恭平

２項定理（あるいは「２項展開」）とは、
(ｘ＋ｙ)^ａの形の式を展開した時にどのようになるかを表した式です。

指数の部分ａは自然数である事も多いですが、一般の実数で同じ形に展開できます。（ただしａが自然数でない場合は有限の数の項で終わらず無限級数になる場合があります。）

指数が自然数の場合
指数が実数の場合（一般２項定理）

指数が自然数の場合

まず、簡単なのはｎを自然数として、(ｘ＋ｙ)^ｎの形の式を展開した場合です。
ただし簡単とは言っても、任意の自然数ｎについてどのようなものになるかを知るには順列と組み合わせの知識が必要です。

ｎ＝２の場合、(ｘ＋ｙ)^２＝ｘ^２＋２ｘｙ＋ｙ^２　であり、

ｎ＝３の場合、(ｘ＋ｙ)^３＝ｘ^３＋３ｘ^２ｙ＋３ｘｙ^２＋ｙ^３　です。

ｎが小さい場合は直接に計算もできますが、じつは公式として書けるというのが２項定理です。

２項定理（指数が自然数の時）

$$(x + y)^n=x^n+n\mathrm{C} _1x^{n-1}y+{}_n \mathrm{C} _2x^{n-2}y^2+{}_n \mathrm{C} _3x^{n-3}y^3+\cdots+{}_n \mathrm{C} _{n-1}xh^{n-1}+y^n$$ $$ =x^n +nx^{n-1}y+\frac{n(n-1)}{2}x^{n-2}y^2+\frac{n(n-1)(n-2)}{3!}x^{n-3}y^3+\cdots+nxy^{n-1}+y^n$$

★順列や組み合わせを学ぶと必ず出てくるものですが、びっくりマークが「！」ついている「3！」は「３の『階乗』」で、3！= 3・2・1 = 6 を表します。4 の階乗なら、4！=4・3・2・1 = 24。ここではあまり関係ないですが「ゼロの階乗」は0！= 1 と「定義」します。

このようになる理由自体は単純で、直接の式の展開を考えてみるのです。

x とｙを何個選ぶかの「組み合わせ」を考えます。

２項定理と組み合わせ — ３つの場所の中からｘを１つ選ぶと、残り２つはｙで決定するので係数は「組み合わせ」の数として決定します。

ｎ＝２やｎ＝３の場合を考えてみると分かりやすいと思いますが、ｘｙやｘ^２ｙの項の係数は結局どういう理由で決まるのかというと、式展開した時にそれらの項が「何個」あるかで決まっています。

ｎ＝３のときのｘ^２ｙの項については「３つの項の中からｘを２個、ｙを１個選ぶ方法」の数に等しいのです。これは、組み合わせで表現できます。

少し分かりにくい場合は、３つの場所①②③を考えて、２つ選ぶという場合を考えてみてください。その２つの場所からｘをぶという考え方でも組み合わせの総数になります。

３つの中から３個ともｘ、３個ともｙを選べばｘ^３とｙ^３の場合であり、そのような組み合わせは１通りだけで実際それらの項の係数は１になります。

つまり、(ｘ＋ｙ)^ｎのｘ^ｍｙ^ｎ－ｍの項の係数が_ｎＣ_ｍになるというのが２項定理の内容です。
組み合わせの性質により、_ｎＣ_ｎ－ｍ＝_ｎＣ_ｍになります。３乗の展開式において係数が１、３，３、１の順で並ぶのはそのためです。

４乗の場合の展開式を計算してみると、_４Ｃ_１＝_４Ｃ_３＝４、_４Ｃ_２＝６であるので、(ｘ＋ｙ)^４＝ｘ^４＋４ｘ^３ｙ＋６ｘ^２ｙ^２＋４ｘｙ^３＋ｙ^４　です。
これは、３乗の展開式に（ｘ＋ｙ）をかけてみても同じ結果になります。

指数が実数の場合（一般２項定理）

上記の指数が自然数の場合の形の式と全く同じ形が、指数が実数一般の場合でも成立する事を特に指して一般２項定理（もしくは一般２項展開）と言います。

この場合はどうやって示すのかというと、結論を言うとマクローリン展開を使います。マクローリン展開とは微積分を利用した関数の無限級数展開の１つで、高校では教えない場合も多いので高校生であれば覚える必要はありません。（テイラー展開の特別な場合がマクローリン展開です。）

参考までに述べておくと一般２項定理の証明は次のようになります。

一般２項定理の証明

a が自然数でない時、$(1+x)^a\hspace{5pt}(|x|＜1)$に対して適用して、マクローリン展開を適用すると、 $$(1+x)^a=1+ax+\frac{a(a-1)}{2}x^2+\frac{a(a-1)(a-2)}{3!}x^3+\frac{a(a-1)(a-2)(a-3)}{4!}x^4+\cdots$$ r ＜ s および s ≠ 0 の任意の実数 r と s の組に対して |x|＜1 の範囲に x = r/s となる x が存在するので、 $$\left(1+\frac{r}{s}\right)^a=1+a\frac{r}{s}+\frac{a(a-1)}{2}\frac{r^2}{s^2}+\frac{a(a-1)(a-2)}{3!}\frac{r^3}{s^3}+\cdots$$ $$\left(1+\frac{r}{s}\right)^a=\left(\frac{s+r}{s}\right)^a=\frac{(s+r)^a}{s^a}に注意して、$$ 上式の両辺にs^ａ（これは有限の値）をかけます。 $$(s+r)^a=s^a+ars^{a-1}+\frac{a(a-1)}{2}r^2s^{a-2}+\frac{a(a-1)(a-2)}{3!}r^3s^{a-3}+\cdots$$ というわけで、a が自然数の場合とも合わせて、一般２項定理が成立する事を意味します。（証明終）
この証明でややこしくて面倒なのは、$(1+x)^a$のマクローリン展開が可能な x の範囲が |x|＜1 という形で限定されているため、最初からマクローリン展開で直接に一般２項定理を示そうとすると話がこじれるところでしょう。

冒頭でも少し触れましたが、このように形としては指数が自然数でもそうでなくても同じ関係式が成立しますが、指数が負の数などの場合では項が延々とずっと続き無限級数になります。（単なる式の展開が無限級数とか微積分との関連もあるというのは、少し意外に思う人もいるかもしれません。）

２項定理が成立するとすると、単項式の微分公式が (ｘ^ａ)’ ＝ｎｘ^ａ－１となる理由が分かりやすくなるという利点があります。（ただしａが実数の場合には、一般２項定理は微分公式の証明にはなりません。指数が実数の場合の単項式の微分公式の証明は、普通は対数関数の微分公式を利用します。）

コーシーの積分定理

恭平

複素関数論の積分の理論における、コーシーの積分定理と、コーシーの積分公式について述べます。両者は名称が似ていて実際極めて近い関係にありますが、式の内容と使い方が少しだけ違うので名称が微妙に分けられているのです。

複素関数の微分、複素関数の積分の基本的な考え方は別途にまとめています。

■ 定理の内容　■ 証明　■ コーシーの積分公式　

定理の内容

コーシーの積分定理とは、積分経路が閉曲線である場合に成立する次の関係式です。

コーシーの積分定理

閉曲線Ｃで囲まれた領域内でｆ(ｚ)が正則である時、$$\int_Cf(z)dz=0$$ ☆ここで、「領域内」とはＣ上の点も含むものとします。

この定理が適用できる条件として領域内で正則であるという事がじつは重要で、１点でも正則でない部分があれば適用はできないのです。

正則でない・・実質的には「微分可能でない」という点は、多くの場合は分母が０になって関数自体定義できないパターンです。しかし、そのような正則でない点が有限個の場合などは、その周囲だけを除いてあげた領域を考えてコーシーの積分定理を適用できたりしいます。その考え方は後述する「コーシーの積分公式」に深く関わります。

しかしこの公式が確かに成立すると分かった時点で、あとは比較的速やかに話が進むのです。

積分定理と積分公式の違い — コーシーの「積分定理」と「積分公式」は一応違うものなので注意しましょう。

定理の証明

複素数の積分については「積分経路を閉曲線にとった場合」には次の式が成立します。

グリーンの公式

$$\int_Cf(z)dz=\int\int_D\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)f(x,y)dxdy$$

このグリーンの公式が成立する根拠については、別途に詳しく述べています。積分の経路が閉曲線であるという事がポイントです。複素関数論の初歩の中で、ここが一番難しい・理解しにくいという人も多いのではないかと思います。

グリーンの公式が成立するという条件のもとでは、「コーシーの積分定理」の証明はそれほど難しくはないのです。

グリーンの公式において、関数ｆ(ｚ)が「正則である」という条件をつけます。これは、大雑把には領域内の任意の点で微分可能であるという感覚です。

この時には、グリーンの公式に加えて、複素数の微分のほうについて「コーシー・リーマンの関係式」が成立します。ｆ(ｚ)＝ｕ(ｘ,ｙ)＋ i ｖ(ｘ,ｙ)とした時の、ｕとｖに対する偏微分についての関係式です。

これを使う：コーシー・リーマンの関係式

$$f(z)=u(x,y)+iv(x,y)が正則である時、\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},かつ\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$$

グリーンの公式の積分の中身を、ｕとｖで表してみます。

$$\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)f(x,y)=\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)(u+iv)$$

$$=i\frac{\partial u}{\partial x}-\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}-i\frac{\partial v}{\partial y}$$

$$=-\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)+i\left(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\right)$$

こういうふうになるので、経路Ｃが閉曲線でｆ(ｚ)が正則という条件なら、関数と経路の形によらず定積分の「積分の中身」の値がうまい具合に必ずゼロになるので、定積分の値もゼロになるという事です。

$$f(z)が正則ならば\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)f(x,y)=-\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)+i\left(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\right)=0$$

$$したがって、f(z)が正則ならば\int_Cf(z)dz=\int\int_D\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)f(x,y)dxdy【証明終り】$$

この定理は、別に魔法によって不思議に成り立つのではなくて「積分経路Ｃが閉曲線で領域内でｆ(ｚ)が正則」という、言ってみれば特殊な条件を課して限定する事によって成立するのです。

コーシーの積分公式

もう１つ重要なものとして、名称が少し紛らわしいのですが「コーシーの積分公式」というものがあります。これは、コーシーの「積分定理」のほうから導出されるものです。

コーシーの積分公式

$$f(z)=\frac{1}{2\pi i}\int_C\frac{f(\zeta)}{\zeta-z}d\zeta$$ この公式の積分の中身の中のｚは、積分変数に対しては定数扱いであり、積分変数（複素数）としては「ゼータ」を文字として使っています。
この関係式の詳細について、次に述べていきましょう。

コーシーの「積分定理」が適用できる複素関数と領域があったとします。そこで、領域内のてきとうな複素数ｚ＝ｗを考えて、関数をｚ－ｗで割ります。

$$\frac{f(z)}{z-w}を考えます。$$

ｆ(ｚ)が微分可能なら、それをｚ－ｗで割った関数も微分可能です。

ただし、ｚ＝ｗを除きます。

ｚ＝ｗにおいては、関数が定義されないので、当然微分不可能というわけです。
このように、わざと「微分不可能で正則でない点」を考えて、関数にくっつけているのです。

こういう場合に積分はどう考えるのかというと、もとの積分経路に、ｚ＝ｗを囲む（小さな）円を経路として付け足した別の経路を考えてみるのです。なぜ「円」を考えるのかというと、これは閉曲線の中では最も計算しやすいためです。

その円周の経路をＣ１としましょう。もとの経路をＣとし、合わせた経路をＣ＋Ｃ１とここでは書く事にします。積分する時には、次のように経路ごとに項を分ける事ができます。

このとき、小円の経路Ｃ１はその円に関して言えば時計回りに積分が行われています。つまり、小円の経路だけで定積分を考えた場合、本来の符号とは逆であり、そのためマイナス符号をつけます。

$$\int_{C+C1}\frac{f(z)}{z-w}dz=\int_C\frac{f(z)}{z-w}dz-\int_{C1}\frac{f(z)}{z-w}dz$$

ここで、経路Ｃ＋Ｃ１に対してコーシーの積分定理を使います。
（その領域においてｚ＝ｗは除外されていて、含まれていない事に注意します。）

$$0=\int_C\frac{f(z)}{z-w}dz-\int_{C1}\frac{f(z)}{x-w}dz\Leftrightarrow \int_C\frac{f(z)}{z-w}dz=\int_{C1}\frac{f(z)}{x-w}dz$$

ここで、小円の経路Ｃ１のほうについて、ｚ＝ｗ＋ｒe^iθと置きます。これは、ｚ＝ｗを中心とした円周上の点を媒介変数表示したものです。ｒは何かてきとうな（小さい）実数であり、媒介変数はθです。

このとき、ｚ－ｗ＝ｒe^iθですから、分母が簡単になるという１つのカラクリがあります。変数変換をしていますので微分も必要になりますが、この場合指数関数の微分ですから計算は容易なのです。

$$\frac{dz}{d\theta}=rie^{i\theta}と合わせて、\int_{C1}\frac{f(z)}{x-w}dz=\int_0^{2\pi}\frac{f(w+re^{i\theta})}{re^{i\theta}}\frac{dz}{d\theta}d\theta$$

$$=\int_0^{2\pi}\frac{f(w+re^{i\theta})}{re^{i\theta}}rie^{i\theta}d\theta =\int_0^{2\pi}if(w+re^{i\theta})d\theta$$

このように上手い具合に分母と、変数変換による微分の項が打ち消して消えます。

ここでｒ→０の極限を考えます。すると、f(ｗ＋ｒe^iθ) → ｆ(ｗ)です。（これは、より厳密には上限で上から抑える不等式で示します。）

すると、次のようになるような、じゅうぶん小さいｒを必ず考える事ができるという事です。

$$\int_{C1}\frac{f(z)}{x-w}dz=i\int_0^{2\pi}f(w)d\theta=if(w)\left[\hspace{3pt}\theta \hspace{3pt}\right]_0^{2\pi}=i(2\pi-0)f(w)=2\pi if(w)$$

定積分の計算の最後のところは、ｆ(ｗ)が（θに関して）定数であるのでこのようにできるという事です。

整理しますと、結局次のように言えます。

$$\int_C\frac{f(z)}{z-w}dz=2\pi if(w)\Leftrightarrow f(w)=\frac{1}{2\pi i}\int_C\frac{f(z)}{z-w}dz$$

ここで、もとの閉曲線Ｃで囲まれた領域内の点ｗは、何か特別な点ではなく、領域内の任意の点でよかったわけです。ｗを変数ｚに置き換えて、積分の中の変数を何か別のてきとうなものを使っても同じ意味になります。このように、領域内の任意の複素数ｚにおけるｆ(ｚ)を積分で表したものがコーシーの「積分公式」です。

改めてコーシーの積分公式

$$f(z)=\frac{1}{2\pi i}\int_C\frac{f(\zeta)}{\zeta-z}d\zeta$$ この公式の積分の中身の中のｚは、積分変数に対しては定数扱いです。
また、上記の「コーシーの積分定理」との違いに注意してみてください。「コーシーの積分公式」は、複素関数の値自体を積分で表す公式です。

積分の中の変数の記号は別に何を使ってもよいのですが、「複素数の」変数である事を強調するためにギリシャ文字の「ゼータ」を使う事が多いようです。ここでもその表記を使っています。ｔなどを使っても別によいのですが、これは媒介変数として実数の変数を表す事が多いので、積分変数としてゼータを使用する事は、なるべく誤解を避けるための習慣であろうかと思います。

複素数の微積分の理論はこの先も続いていきますが、初歩的な理論としてはここまで理解していればそれほど難解な理論は少ないと思います。

変数分離形の微分方程式の解法

恭平

常微分方程式のうち、変数分離形と呼ばれるタイプの解法について説明します。

「変数分離形」の常微分方程式とは？
一般的解法の手順
具体例

変数分離形の常微分方程式は、一般的な微分方程式論の中では最も初歩的な形の微分方程式として扱われるものです。

ただし、このサイトではより高校数学の延長線上にあって入りやすく、かつ物理学での基礎理論で使われるため学ぶ意味も分かりやすいという意味で、最も簡単な部類の微分方程式を別途に挙げてまとめています。一般的な変数分離形の微分方程式よりも、それらのほうがはるかに解くのは簡単でしょう。（形式的にはそれらの中に変数分離形として扱えるものもありますが、専用の公式を使うメリットがありません。）

「変数分離形」の常微分方程式とは？

■ 定義　■ 具体例　■ 名前の由来　

定義

まず、どういうものが変数分離形と呼ばれるのかについてです。

一応これは微分方程式論の中で決められています。

ｙ＝ｙ(x) すなわちｙがｘの関数の時に、次の形を持つ常微分方程式を変数分離形と呼びます。

変数分離形の常微分方程式 $$\frac{dy}{dx}=F(x)G(y)$$ の形をしている常微分方程式を「変数分離形」であると呼びます。
ここで、ＦやＧはｙ＝ｙ(ｘ)とは別の関数です。

このように定義はあるわけですが、これだけではちょっと分かりにくいと思います。そこで、具体的にどういうものが該当するのか挙げてみましょう。

具体例

Ｆ(ｘ)Ｇ(ｙ)という積の形ですが、具体的な形としては「割り算」になっていてもよい事に注意しましょう。これは、Ｇ(ｙ)＝１／｛ｇ(ｙ)｝のような関数を考えてもよいためです。

具体例：変数分離形の常微分方程式

$$\frac{dy}{dx}=x^2y$$ $$\frac{dy}{dx}=\frac{x}{y}$$ $$\frac{dy}{dx}=\frac{y^2-1}{x}$$ $$\frac{dy}{dx}=\frac{y^3}{x^2+1}$$ $$\frac{dy}{dx}=\frac{x}{\sin y}$$

右辺が実質的にｘだけ、ｙだけで表される場合も該当します。 $$\frac{dy}{dx}=x+1$$ しかしこのような簡単な微分方程式の場合は変数分離形とみなさずに直接解を出してしまったほうが早い場合も多いと思います。

これらのように、確かに右辺がＦ(ｘ)Ｇ(ｙ)の形になるものが該当します。

また、これらの他に、一見するとその形になっていなくても、変数変換をする事で変数分離形にする事ができるパターンのものが存在します。（「変数分離形に『帰着』できる」とよく言います。）

変数変換で変数分離形に帰着できるパターン

例えば次のようなものです。 $$\frac{dy}{dx}=x+y-1\hspace{4pt}\cdots\hspace{4pt}u=x+y-1とおくと\frac{du}{dx}=1+u$$ $$\frac{dy}{dx}=\frac{x^2-y^2}{2xy}\hspace{4pt}\cdots\hspace{4pt}u=\frac{y}{x}とおくと\frac{du}{dx}=x\left(\frac{1-3u^2}{2u}\right)$$ このように変数変換でうまくいくパターンには特徴がある場合も多くて、例えば次の２つの形のタイプは変数変換で変数分離形に変形できます。 $$\frac{dy}{dx}=F\left(\frac{y}{x}\right)の形のもの$$ $$\frac{dy}{dx}=F(ax+by+c)の形のもの$$

名前の由来

解法に関わる事ですが、ｄｙ／ｄｘを「形式的」に割り算と見なした時に
Ｇ(ｙ)ｄｙ＝Ｆ(ｘ)ｄｘの形に変形ができる事が変数分離形の常微分方程式の特徴です。

数学の微積分学・解析学ではｄｙ／ｄｘは極限値を表す１つの記号と約束するのですが、ｄｙとｄｘを「分離する」考え方は数学の微分方程式論でも扱われる場合があります。

形式的な変数分離形の常微分方程式の捉え方

変数分離形の常微分方程式は、次のように形式的に書かれる場合もあります。 $$G(y)dy=F(x)dx$$

一般的解法の手順

■ ①ｘとｙの関数を両辺に分離する　■ ②両辺を積分変数ｘで積分する　■ 変数変換を含む場合の解法　

①ｘとｙの関数を両辺に分離する

まず、両辺をＧ(ｙ)（≠０）で割ります。（実質的には乗じる事になる場合もあります。）

$$G(y)\neq 0のもとで\frac{dy}{dx}=F(x)G(y)\Leftrightarrow \frac{1}{G(y)}\frac{dy}{dx}=F(x)$$

このとき、同時に両辺に「ｄｙをかける」と説明がなされる事もあります。それでも微分方程式を解く事はできますが、ここではそれはやらないで話を進めましょう。

②両辺を積分変数ｘで積分する

次に、両辺を積分変数ｘで積分します。微分方程式の一般解法では、普通は不定積分を考えます。この時、積分定数も書いてもいいのですが、ここでは積分定数は不定積分に含まれていると考えて、全ての積分記号がなくなった時に積分定数を書く方法を採用します。

$$\int \frac{1}{G(y)}\frac{dy}{dx}dx=\int F(x)dx$$

この左辺は置換積分の形になっていますから、積分変数をｙに変える事ができます。もし定積分である場合は、もちろん積分区間についてもきちんと対応させて変えなければなりません。

$$\int \frac{1}{G(y)}\frac{dy}{dx}dx=\int\frac{1}{G(y)}dyにより、$$

$$\int\frac{1}{G(y)}dy=\int F(x)dx$$

この形にする事で、具体的に積分を計算して解とするのです。

★この時の置換積分の操作を省略して「両辺を積分すると」などと言う事もあります。ただし、微積分学的には置換積分によって結果的にそういう事ができる、という事です。

ただし、ここで具体的な積分計算がしやすいとは限らず、ものによっては手計算では手に負えない場合もあります。一般論としての解法は、あくまで上記の形には確実に変形できるという事を言っています。

そこから先は、同じ変数分離形であっても、個々の微分方程式の形によって簡単に解けるか手計算ではてこずる内容であるかは大きく変わってくるのです。

変数変換を含む場合の解法

次の形のものは、変数変換によって変数分離形に変形できることを簡単に前述しました。

$$\frac{dy}{dx}=F\left(\frac{y}{x}\right),\hspace{5pt}\frac{dy}{dx}=F(ax+by+c)の形のもの$$

まず前者については次のようにします。ｕ＝ｙ／ｘと変数変換します。

$$u=\frac{y}{x}\Leftrightarrow y=ux\Rightarrow\frac{d}{dx}y=\frac{d}{dx}(ux)$$

$$\Rightarrow\frac{dy}{dx}=\frac{du}{dx}x+u$$

ｙ＝ｕｘの両辺を「ｘで」微分しています。右辺については、積の微分公式を使っています。（ｙはｘの関数なのでｕもｘの関数と考える事ができる事に注意。）

さてここで、ｄｙ／ｄｘについてはもとの微分方程式をそのまま代入できます。

$$\frac{dy}{dx}=F\left(\frac{y}{x}\right)=F(u)であったから、F(u)=\frac{du}{dx}x+u$$

$$∴\frac{du}{dx}=\frac{F(u)-u}{x}$$

このようになるので、Ｆ(ｕ)－ｕという新たなｕに関する関数と、１／ｘという関数で構成される変数分離形になるわけです。これによってｕをｘで表し、ｕをｘとｙの形に直せばｘとｙの関係式が得られます。

★微分方程式一般について言える事ですが、積分の計算ができたとしても必ずしもｙ＝ｆ(ｘ)の形にならずにｆ(ｘ,ｙ)＝０の形になる場合もあります。これを微分方程式の解の「陰関数表現」と言います。

変数変換できるパターンの２つ目のタイプも見てみましょう。

これはもっと簡単で、ｕ＝ａｘ＋ｂｙ＋ｃとおいて、両辺をｘで微分します。

$$\frac{du}{dx}=a+b\frac{dy}{dx}$$

これに、もとの微分方程式ｄｙ／ｄｘ＝Ｆ(ａｘ＋ｂｙ＋ｃ)＝Ｆ(ｕ)を代入するのです。

$$\frac{du}{dx}=a+bF(u)$$

この場合、ａ＋ｂＦ(ｕ)という関数を新たなｕの関数と考えますこの時ｘのほうの関数は定数関数１です（もちろん最終的にはｕをｘで表せます）。

ａ＋ｂＦ(ｕ)≠０のもとでこの関数で両辺を割り、積分操作をします。
ここでは置換積分の箇所は省略して記しましょう。

$$\int \frac{1}{a+bF(u)}du=\int dx=x+C$$

この場合については定数関数１をｘで積分してｘという関数が必ず出てきます。

具体例

■ 普通の変数分離形の場合　■ 面倒くさい例　■ 変数変換を使う例　

普通の変数分離形の場合

では、具体例として次の微分方程式を解いてみましょう。まず簡単な例です。

$$\frac{dy}{dx}=\frac{3x^2}{y}$$

両辺にｙをかけて、変数を両辺に「分離」します。

$$y\frac{dy}{dx}=3x^2$$

積分操作をします。（置換積分部分を省略します。）

$$\int ydy=\int 3x^2dx$$

$$\frac{1}{2}y^2=x^3+C$$

ｙ＝ｙ(ｘ)の形に直すなら次の形になります。

$$y=\pm\sqrt{2x^3+C}$$

少々汚い形ですが、これが正しいかどうかはｘで微分をしてみる事でチェックできます。

$$\frac{dy}{dx}=\pm\frac{1}{2}\frac{3\cdot 2x^2}{\sqrt{2x^3+C}}=\frac{3x^2}{\pm\sqrt{2x^3+C}}=\frac{3x^2}{y}$$

面倒くさい例

さて次の例は、考え方は同じですが積分計算が面倒な例です。
ただし手計算で計算できます。

$$\frac{dy}{dx}=\frac{y^2-1}{2x}$$

両辺をｙの関数（右辺の分子の関数）で割ります。

$$\frac{2}{y^2-1}\frac{dy}{dx}=\frac{1}{x}$$

この時の定数係数の「２」は右辺に持っていっても左辺に持っていってもどちらでも解けます。ただ、これについては左辺に置いた方がじつは計算が楽です。

積分操作を試みます。

$$\int \frac{2}{y^2-1}dy=\int\frac{1}{x}dx$$

さて、右辺は対数関数で表せますが左辺はどうでしょう。
これは結局、普通の積分の練習問題になります。

結論を言うと、この場合は「部分分数分解」で手計算により処理可能です。

$$\int \frac{2}{y^2-1}dy=\int \frac{1}{y-1}dy-\int \frac{1}{y+1}dy$$

$$=\ln |y-1|-\ln |y+1|+C_0=\ln \left|\frac{y-1}{y+1}\right|+C_0$$

変数分離形の常微分方程式② — 具体的な積分の項の計算の段階になると、微分方程式というよりは初等関数の積分の計算の練習問題になります。

よって、微分方程式は次のように解けます。積分定数はＣひとつにまとめます。

$$\ln \left|\frac{y-1}{y+1}\right|=\ln |x|+C$$

この場合はさらに式を簡単にできてｙ＝ｙ(ｘ)の形にもできます。（定数部分を指数関数の形で表せば右辺を１つの対数関数としてまとめられます。最後の定数は新たに設定します。）

$$\frac{y-1}{y+1}=x+C_1\hspace{5pt}∴y=\frac{1+C_1x}{1-C_1x}$$

変数変換を使う例

参考までに、変数変換を使う具体例の解法も１つ記しておきます。

$$\frac{dy}{dx}=\frac{x^2-y^2}{2xy}\hspace{4pt}\cdots\hspace{4pt}u=\frac{y}{x}とおくと\frac{du}{dx}=x\left(\frac{1-3u^2}{2u}\right)$$

この変換の過程について補足しておくと次のようになります。

$$\frac{x^2-y^2}{2xy}=\frac{1}{2}\left(\frac{x}{y}-\frac{y}{x}\right)=\frac{1}{2}\left(\frac{1}{u}-u\right)$$

$$F(u)=\frac{1}{2}\left(\frac{1}{u}-u\right)$$

$$F(u)-u=\frac{1}{2}\left(\frac{1}{u}-3u\right)=\frac{1-3u^2}{2u}$$

ｘとｕに関する微分方程式になった時点で、ｘとｕを分離します。ここでは積分までまとめて記しましょう。分母が零にならない条件で次のようになります。

$$\int\frac{2u}{1-3u^2}du=\int \frac{1}{x}$$

この積分の右辺は対数関数で表せますが、じつは左辺も対数関数で表せるのです。

$$-\frac{1}{3}\ln |3u^2-1|=\ln |x| +C$$

のようになり、これも対数を取り払ってｕとｘ、ｙとｘの関係式で表す事もできます。

この変数分離形の微分方程式は、物理学や工学の理論で使う場合もありますが、一般の解法についてはむしろ数学の微分方程式論の中の１つの位置付けとして見ておいたほうがよいのではないかと思います。

複素数の積分

恭平

複素数の微分に続いて、このページでは複素数の積分について述べます。
これは学校での授業としては大学数学の範囲になります。

定義と考え方

■ 積分をどのように定義する？
■ 複素関数の定積分には「積分経路」が必要
■ 複素数の積分・・何に使う？　

積分をどのように定義する？

複素関数の微分は比較的分かりやすいかと思いますが、
では複素関数のの積分は一体どのように定義するのかという話になります。

考え方は、実数関数の積分と同じく、「和」を考えます。

ｚ＝ｘ＋ i ｙのときに、ｄｚ＝ｄｘ＋ i ｄｙを考えるのです。

そして、複素関数ｆ(ｚ)に対してｆ(ｚ)ｄｚ＝ｆ(ｚ)ｄｘ＋i ｆ(ｚ)ｄｙを考え、加え合わせます。
これが複素関数の積分です。

複素関数の積分（定積分）

$$\int_Cf(z)dz=\int_Cf(z)(dx+idy)=\int_C(u+iv)(dx+idy)=\int_C(udx-vdy)+i\int_C(vdx+udy)$$

ｆ(ｚ)＝ｕ(ｘ,ｙ)＋iｖ(ｘ,ｙ)です。
積分記号に添えられているＣとは、後述する「積分経路」です。

微小な領域の幅に相当するものを関数に乗じて加え合わせて極限を取るという考えが得方は実関数の積分の場合と同じなのです

ｘとｙが媒介変数ｔ(実数)で結ばれる時は、このｔによって複素変数ｚが定まるので、ｔによる積分と考える事もできます。

これら２つの複素関数の積分の定義は同等なものとなります。

媒介変数を使った複素関数の積分（定積分）

$$\int_Cf(z)dz=\int_a^bf(z(t))\frac{dz}{dt}$$

この場合、媒介変数ｔは実数です。
ｔの積分区間 [a, b] において、あたかも通常の実関数であるかのように定積分を行う事になります。
積分経路が円の時は、媒介変数として弧度法の角度θを使う事が多いです。

複素関数の定積分には「積分経路」が必要

さて、実数関数の場合の定積分には「積分区間」がありました。複素関数の場合にもそれに相当するものがありますが、じつは積分の区間ではなく「経路」が必要になります。

単純にｘを動かして次にｙを動かした場合、それは多くある積分経路の１つです。

積分経路は、直線であったり、曲線であったり、円のような閉曲線でもあり得ます。

このような積分経路が定められた時、ｚ＝ｘ＋ i ｙのｘとｙには従属関係があります。

$$例えば直線であればy=2x,円であればx^2+y^2=1といった関係です。$$

このような時には媒介変数ｔでｘとｙを結ぶ事ができます。円の場合には、媒介変数は角度で考える事が普通です。

積分経路上の１つ１つの点に対して、複素関数ｆ(ｚ)の値が存在する形になります。

積分経路が閉曲線の場合、基本的には「反時計回り」が正の方向です。もう少し詳しく言うと「経路を進む方向に対して領域が常に左側に来るように」正の向きをとります。

この向きの取り方は閉曲線の中に別の閉曲線による「穴が」あるような場合の正の向きの考察に役立ちます。（そのような場合も一番外側の閉曲線を「反時計回り」で考える事で正しく向きを処理する事も可能です。）

どの向きをプラスにとるのかについて、反時計回りに考える方法と「左手側に領域が来るように」という方法は本質的に同じものです。領域内に穴があるような場合には、定積分が打ち消してゼロになる補助線を引いて考えます。

複素数の積分・・何に使う？

複素数の積分は間接的に物理等の理論に関わり、数学上も時折使う事のあるツールの１つとしてところどころで顔を出します。

まず１つは、特定の実数関数の定積分（多くの場合積分区間を無限大にする「広義積分」ですが）の値を出すのに、複素積分を使う事があります。あるいは、そのような手順を踏まないと手計算では値を出せないと言ったほうがよいでしょう。そういった種類の定積分があるわけです。

もう１つは、分母に変数があり、その変数が０になってしまう場合（「極」と言います）の処理のために複素積分の考え方をうまく使える場合があります。これについては「コーシーの積分公式」との関連が深いです。

数学の理論の中では「代数学の基本定理」について、複素数の積分の理論の一部を適用する事によって証明が可能です。（他の方法でも証明はできます。証明の方法は多いです。）

仕事と運動エネルギーとの関係

恭平

このページでは古典力学での「仕事」と、運動エネルギーとの関係について述べます。
数学的には、ベクトルの微積分の応用であり、ベクトルの内積の応用でもあります。

内積と「仕事」
仕事と運動エネルギーの関係式の導出

内積と「仕事」

平面や空間での物体の運動を考える時、力のベクトルの向きと、現に運動している物体の運動の方向・・・つまり速度ベクトルの方向は、互いに異なるという事も普通にあります。

例えば、床に置かれた重い物に紐を付けて斜めに引っ張ったところ床に対して引きずるように水平に動いたとすれば、力ベクトルは斜め上方向、速度ベクトルは水平方向という事になります。

このような時に力ベクトルと速度ベクトルとの「内積」を考えます。
そしてそこから、「仕事」という量を積分を使って定義します。

☆詳しくは、ここで使う積分は接線線積分と呼ばれるものです。

$\overrightarrow{F}\cdot \overrightarrow{dx}（または \overrightarrow{F}\cdot \overrightarrow{\Delta x}）$ を、物理学では「仕事」と呼びます。
これを経路に沿って合計した量（積分値）を「仕事量」と呼ぶ事があります。

◆仕事はベクトルの内積ですので、
$\overrightarrow{F}\cdot \overrightarrow{dx}=|\overrightarrow{F}|\hspace{2pt} |\overrightarrow{dx}|\cos\theta$ のようにも書く事ができます。
マイナスの値になる事もあり、その場合にも物理的な意味を持ち、角度とその余弦も力と物体の運動に対応したものになります。

この「仕事」を考える事により、じつは「『力』と『物体の運動』と『エネルギー』」を数式的に関連付ける事ができるのです。

運動方程式が成立しているとすれば、その事は数学的に導出できます。結論の関係式は次のようになります。

仕事とエネルギーの関係

関係式は次のようなものです。 $$\int_{t_1}^{t_2}\overrightarrow{F}\cdot \frac{d\overrightarrow{x}}{dt}dt=\frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2$$ 左辺の積分は仕事量、右辺は時間の区間の始まりと終わりでの運動エネルギーの差です。
左辺と右辺とで物理学的な単位は等しく、ともに[J]（ｼﾞｭｰﾙ）です。

意味としては、なされた「仕事」の量と運動エネルギーの増減の量は等しいという事です。

この関係式の数学的な導出には、微分の基本公式とベクトルの微積分が直接的に関係しています。

仕事と運動エネルギーの関係式の導出

まず運動方程式をベクトルの形で書いて、両辺に対して速度ベクトルとの内積を考えます。

$$【運動方程式】 \overrightarrow {F}=m\frac{d^2\overrightarrow{x}}{dt^2} $$ $$【速度ベクトルとの内積】 \overrightarrow {F}\cdot \frac{d\overrightarrow{x}}{dt}=m\frac{d^2\overrightarrow{x}}{dt^2}\cdot \frac{d\overrightarrow{x}}{dt}$$

運動方程式の加速度を含む側について、加速度は位置座標を表すベクトルの時間による２階微分である事に注意します。この部分と、速度ベクトルの内積を考えると、「２階微分と１階微分の積」という、一見わけの分からないものが出てきます。これは一体何でしょう？

それについての数式的な解釈は次のように行います。
合成関数に対する微分公式を用いると、「関数の２乗」を微分すると１階微分が積の形でくっついてくる事が分かります。
すると、「１階微分の２乗」を（１回）微分すると、「２階微分と１階微分の積」が出てくるのです。この時、２という係数も出てきますから１／２を乗じて係数調整を行います。

計算を進めると、じつは次のように変形できます。

$$ \overrightarrow {F}\cdot \frac{d\overrightarrow{x}}{dt}=\frac{d}{dt}\frac{m}{2}\left|\frac{d\overrightarrow{x}}{dt} \right|^2$$

計算

具体的な数式を見てみましょう。
まず、ベクトルではなくてｔを変数とする１変数関数ｘ＝ｘ(t) について考えてみます。 $$\frac{dx}{dt}\frac{d^2x}{dt^2} などは、異なる導関数同士の「積」です。$$ $$\frac{d}{dt}\left\{\frac{m}{2}\left(\frac{dx}{dt}\right)^2\right\}=2\cdot\frac{m}{2}\frac{dx}{dt}\frac{d^2x}{dt^2}=m\frac{dx}{dt}\frac{d^2x}{dt^2}$$ ２乗の部分の微分については、合成関数の微分公式を使っています。
質量ｍは定数扱いです。
これがベクトルの各成分$x_1, x_2, x_3$ （それぞれ時間ｔの関数）について言えます。
そこで、次のように内積を考えるのです。 $$m\frac{d^2\overrightarrow{x}}{dt^2}\cdot \frac{d\overrightarrow{x}}{dt}=m\frac{dx}{dt}\frac{d^2x_1}{dt^2}+m\frac{dx}{dt}\frac{d^2x_2}{dt^2}+m\frac{dx}{dt}\frac{d^2x_3}{dt^2}$$ $$=\frac{d}{dt}\frac{m}{2}\left(\frac{dx_1}{dt}\right)^2+\frac{d}{dt}\frac{m}{2}\left(\frac{dx_2}{dt}\right)^2+\frac{d}{dt}\frac{m}{2}\left(\frac{dx_3}{dt}\right)^2$$ $$=\frac{d}{dt}\frac{m}{2}\left\{ \left(\frac{dx_1}{dt}\right)^2+\left(\frac{dx_2}{dt}\right)^2+\left(\frac{dx_3}{dt}\right)^2 \right\} $$ $$=\frac{d}{dt}\frac{m}{2}\left|\frac{d\overrightarrow{x}}{dt} \right|^2$$ 最後のところは、$$\frac{d\overrightarrow{x}}{dt}=\left(\frac{dx_1}{dt},\frac{dx_2}{dt},\frac{dx_3}{dt} \right) というベクトルの「大きさの２乗」$$を考えているのです。物理的な意味としては、これは物体の速度ベクトルの大きさの２乗、つまり「速さ」の２乗を意味します。内積の計算によって各成分を含む項の和が出てきて、うまい具合に「速さ」になっている事に注意してみてください。

「速度ベクトルのｘ成分の２乗」を時間ｔで微分すると、
「速度ベクトルのｘ成分の２乗」の２倍と、「加速度ベクトルのｘ成分」との積になります。
数学の合成関数の微分公式を使用しています。

変形して得られた式の両辺をてきとうな時間 $t_1,t_2$ で定積分したものを考える事で、仕事量と運動エネルギーの関係式が得られます。

$$\int_{t_1}^{t_2}\overrightarrow {F}\cdot \frac{d\overrightarrow{x}}{dt}dt= \int_{t_1}^{t_2}\frac{d}{dt}\frac{m}{2}\left|\frac{d\overrightarrow{x}}{dt} \right|^2dt= \frac{1}{2}m{v_2}^2-\frac{1}{2}m{v_1}^2$$

「運動エネルギー」は次式で定義します。記号は、Ｔを使う事が多いです。

$$T=\frac{1}{2}mv^2\left(=\frac{m}{2}\left|\frac{d\overrightarrow{x}}{dt} \right|^2\right)$$

この量は正の仕事がなされれば増加し、負の仕事がなされれば減少します。また、仕事がなされなければ運動エネルギーは変化しない、という事も意味します。
（※数学的な定義においても内積は正の値だけでなくゼロや負の値も取り得るものであり、図形的な意味も持つわけです。）

この運動エネルギーに加えて、さらに「位置エネルギー」というものを考え、両者の和を「力学的エネルギー」と呼びます。重力等の「保存力」のみが働いている場合、力学的エネルギーの保存則が成立します。

また、実験・観測から定量的（※）な意味でのエネルギーの等価性が確認されています。運動エネルギーは量としては熱エネルギーや電気エネルギーに変換されると見なす事ができて、物理学だけでなく種々の工学等での理論計算に用いられています。

（※）「定量的に」と言うのは、例えば「力学的エネルギーの『入力』が電気エネルギーと熱エネルギーの『出力』に等しい」といった計算ができるという意味になります。発生する熱エネルギーに関しては、望んでいるものでなければ「損失」と呼ぶ事も多いです。

熱なども含めて考えると、一般的にエネルギー全体についての保存則が成立します。
例えば摩擦によって物体が停止すれば当然ですが運動エネルギーはゼロになりますが、この時にエネルギーの量自体はどこかに消えたというよりは、同じ量の熱エネルギーに変換されたと考えて考察が行われます。

■関連コンテンツ（サイト内リンク）