投稿者: 恭平

三角形の相似

恭平

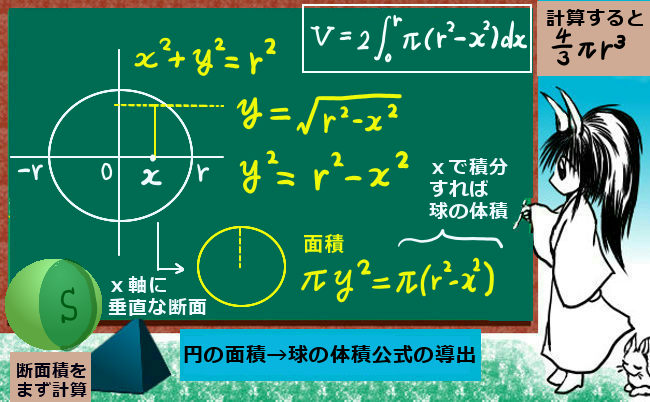
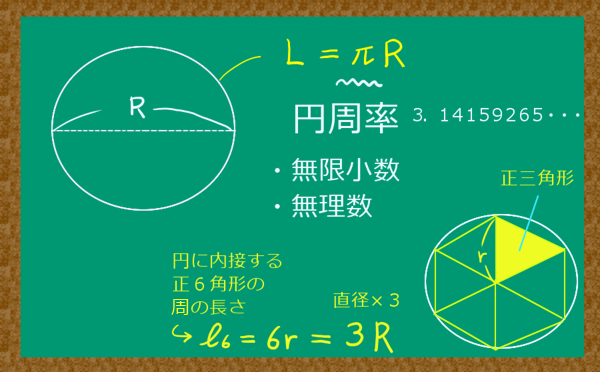
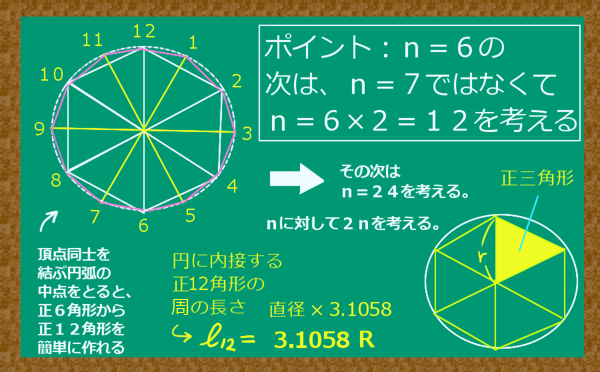
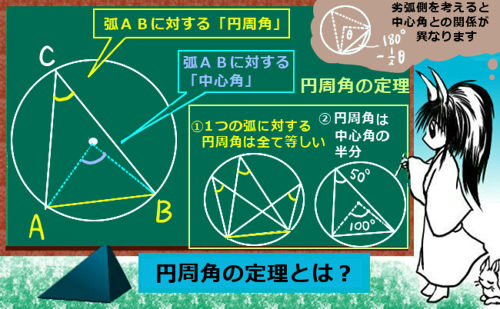
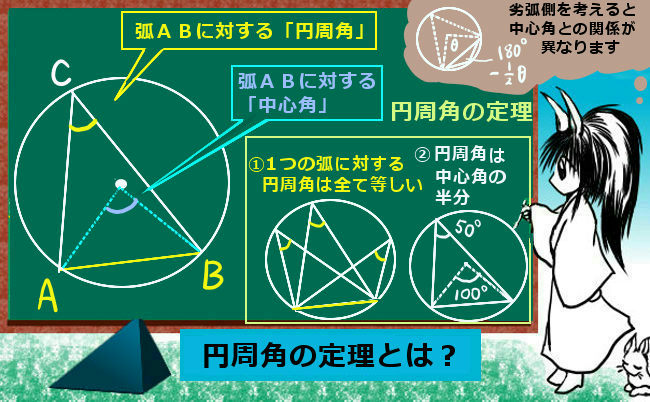
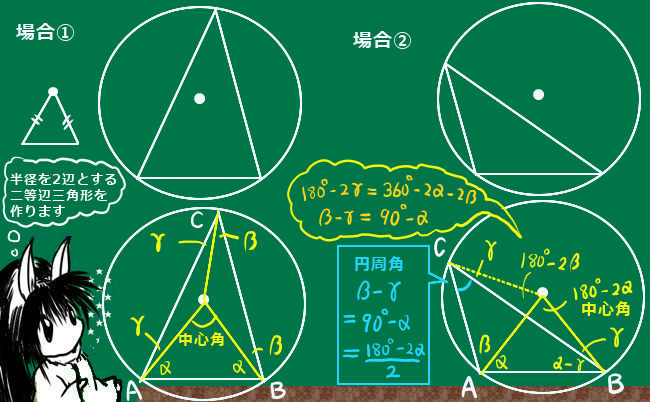
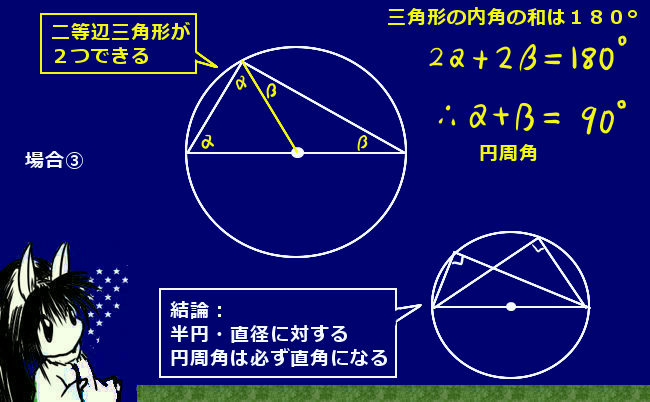
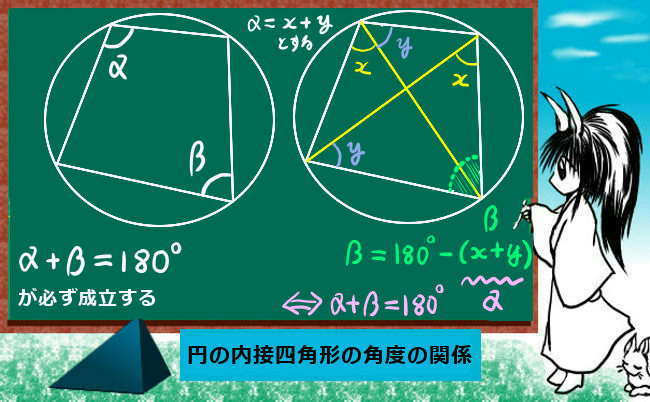
三角形の相似条件は高校入試を始めとして中学数学では重要事項の１つです。

図形問題を解くために必要という事でもありますが、三平方の定理などの重要な定理が成立するための根拠の１つになっている事なども重要と言えるでしょう。

平面において２つの三角形が「相似【そうじ】」であるとは、
ごく簡単に言うと「大きさは違うが形は同じ」であるという事です。

★これに対して、「大きさも形も同じ」なのが三角形の合同です。
意味する事と、成立する条件の違いに注意しましょう。
合同と相似は一見似ていますが扱い方が違うものなので、気を付けましょう。
「２つの三角形が互いに合同」ならば「２つの三角形は互いに相似でもある」と、確かに言えます。 しかしこの逆は成り立ちません。「相似であるから合同でもある」と言ったら、それは間違いです。
【※中学数学の範囲外になりますが詳しくは必要条件と十分条件の関係から把握する事になります。合同である事は相似である事を含んでいるという包含関係になります。】
そのため、合同と相似をごっちゃにしてはならず、関係を意識しながらも丁寧に別々に整理する事が必要であり、重要でもあるのです。

２つの三角形が合同であるならば、相似でもあるとは言えます。相似であっても合同ではない場合があります。

もっとも、単に見た目が似ているというだけでは相似であるとは言わず、きちんと数学的な条件があります。

相似条件と証明での使い方

次の３つの条件の「いずれか」を満たす２つの三角形は互いに相似であると言います。「いずれか」という事は、「１つでも当てはまればよい」という事です。

２つの三角形が相似であるための条件

次のいずれか１つが成立するならば２つの三角形は互いに相似です。

  1. ２組の角の大きさがそれぞれ等しい
  2. ２組の辺の長さの比と、その挟む角の大きさがそれぞれ等しい
  3. ３組の辺の長さの比がそれぞれ等しい

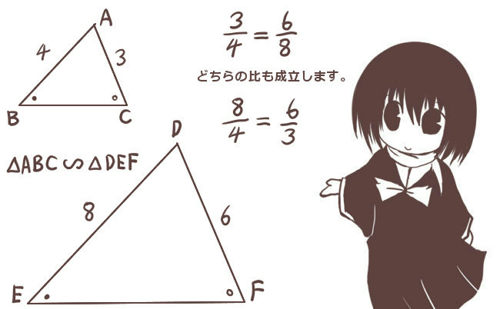
この時「△ＡＢＣと△ＤＥＦは（互いに）相似である」などと言い、△ＡＢＣ∽△ＤＥＦとも書きます。（無限大の記号に似てますが別物です。）この時、「同じ形」として対応する角が順番通りになるように書きます。
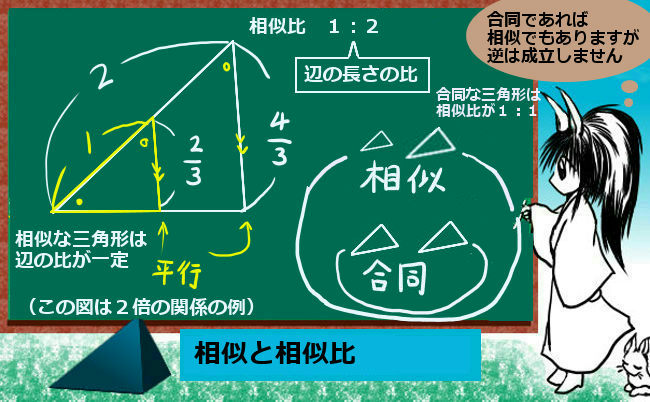
相似な２つの三角形の互いの「辺の長さの比」を相似比と言います。例えば１：２とか１：３という関係が成立します。場合によっては整数比とは限らず、１：\(\sqrt{2}\) とか２：\(\sqrt{3}\) などの相似比もあり得ます。

三角形同士が相似である事がひとたび判明すれば、これら３つの条件は全て成立します。つまり、例えば２組の角度が等しいという条件が成立すれば、３組の辺の長さの比もそれぞれ等しいという事です。

ただし、相似である事を証明するためにはどれか１つだけ判明していればよいという事です。

★比較する２つの三角形が直角三角形であれば、その時点で「対応する１つの角がそれぞれ等しい（９０°で等しい）」事は言えているので、もう１つだけ等しい角度を見つければよいといった作業になります。

繰り返しますが合同条件と似ていますが違うもの（相似条件のほうが制約が緩い）なので注意しましょう。
例えば、辺の長さが分からないけれど角度だけで比較できるのは相似条件のほうであって、合同条件にはそのような条件はないのです。（暗記するのではなく意味を考えてみると分かりやすいと思います。角度だけが分かっている場合、形は同じであっても辺の長さは伸び縮み可能なのです。）

合同である場合は「相似比」が１：１であると言う事もできます。それが「大きさも同じ」という意味であって、大きさが異なる場合には相似比が１：２とか２：３とかになるわけでそのような場合も含めた「形は同じだが大きさは異なる」関係を相似と呼ぶわけです。

２つの三角形が相似である事を正確に見るには、「証明」が必要です。これは、見た感じ「同じ形」に見えるけれど実際は違う（辺の比が一定にならない、角度が異なる）という事があるからです。

高校入試の出題として多いのは「２組の角の大きさがそれぞれ等しい」事を使うパターンです。これは、同じ大きさの角度である部分が２つ見つかればよいという事です。
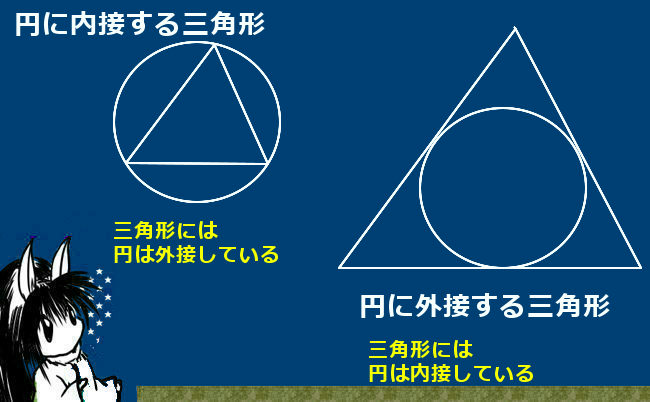
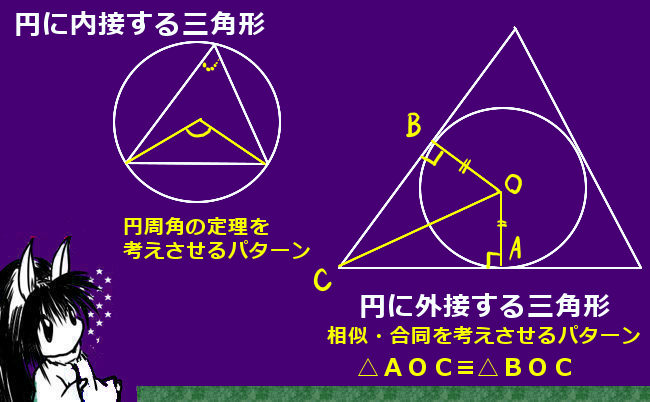
より具体的には、対頂角の関係、平行線の同位角・錯角の関係、円周角の定理などを使って「角度の大きさが等しい」事を示します。また、共有する角がある場合にはもちろんその角度は２つの三角形で等しいのです。

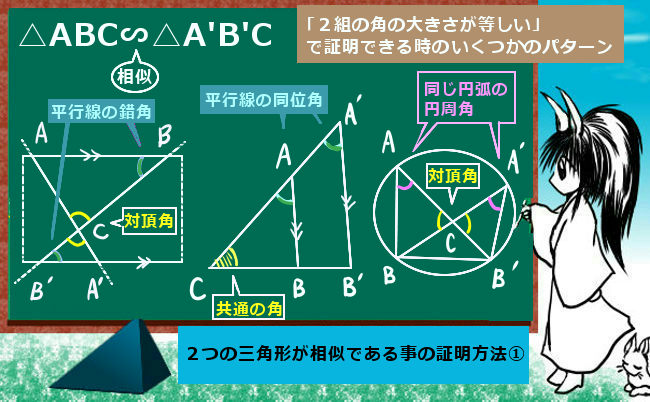
証明のパターン
中学数学・高校入試で問われるパターンはこういったものが多いです。あらかじめ直角三角形という条件が与えられる事で残り１つの角の大きさだけを調べればよい場合もあります。

残りの２条件は証明の時に使う事もありますが、むしろ相似である事が証明された後に辺の比や面積比を計算させる問いで使われる事が多いように思います。

相似な三角形の面積比

三角形の相似比（辺の長さの比）が１：ｎの場合、面積比は１：ｎ２になります。
これは、例えば１つの三角についての底辺がｎ倍、高さについてもｎ倍になるためです。

高校入試ではよく問われる事項です。

相似な２つの三角形の面積比

辺の長さの比が１：ｎの相似な三角形の面積比は１：ｎ２になります。
（辺の長さの比がａ：ｂなら、面積比はａ２：ｂ２）

例えば底辺が２、高さが３の三角形の面積は２×３÷２＝３ですが、
各辺の長さが２倍になったとすると、高さも２倍になる事に注意して
面積は（２×２）×（３×２）÷２＝１２
つまり２×２＝４倍になるという事です。

これは公式として関係式を暗記するのではなく、図に描いてイメージしながら練習してみたほうがよいと思います。

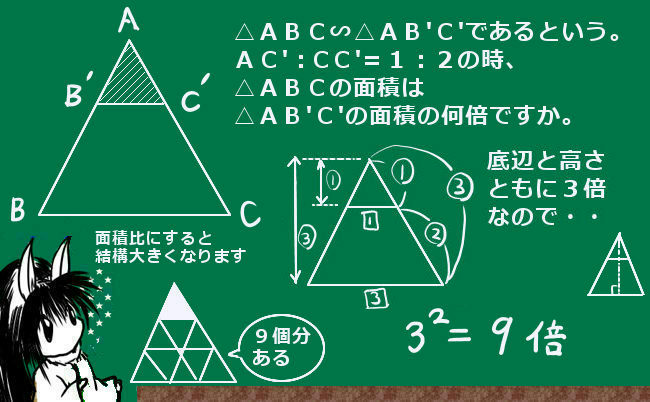
この図の場合、相似な三角形の辺の長さの比は１：３です。相似比が整数のようにきれいな値の場合は図に描いてみて何倍になるのかというイメージをつかむのもよいと思います。平行線の補助線を引く事で図の大きな三角形を９分割できます。三角形の高さも確かに相似比倍になる事については、垂線を補助線として描けば直角三角形についても相似関係が成立する事から分かります。

辺の長さの比が１：３ではなく２：３のような場合は面積比は２２：３２＝４：９です。

$$辺の長さの比が2:3であれば大きい三角形の面積は小さい三角形の\left(\frac{3}{2}\right)^2=\frac{9}{4}倍$$

辺の比に関する補足説明

相似な三角形の辺の比に関して、補足的な説明をします。

三角形同士が相似である場合に「対応する辺同士の比」は等しくこれを相似比と言うのは前述の通りです。

他方で「同じ三角形の中の辺同士の比」も、相似な２つの三角形で等しくなるのです。これは１つの三角形の中で３通りの比がありますからもちろん一定ではなく、一般的に相似比とも異なる値になります。

しかし、例えば△ＡＢＣでＡＢ：ＢＣ＝１：３であったとすると、それに相似な三角形△ＤＥＦがあったときにＤＥ：ＥＦ＝１：３という事も同じく言えるという意味です。
この時、ＡＣ：ＡＢ＝２：５であれば同様にＤＦ：ＤＥ＝２：５という事です。
（※この場合、この条件だけから具体的な相似比は分からない事には注意。互いの対応する辺の長さの比に関して、相似比という一定の比がある事だけ分かります。）

式で書くと、△ＡＢＣ∽△ＤＥＦであれば、
ＡＢ／ＤＥ＝ＡＣ／ＤＦという比の関係（この一定の比が相似比）に加えて
ＡＢ／ＡＣ＝ＤＥ／ＤＦ　という関係も成り立つという事です。

これは、じつは結構単純な話です。
ＡＢ／ＤＥ＝ＡＣ／ＤＦ　の両辺をＡＣで割り、両辺にＤＥをかける事で得られます。
式変形をしなくても相似関係にあるという事は同じ形で大きさだけが異なると意味を考えれば分かりやすいかと思います。

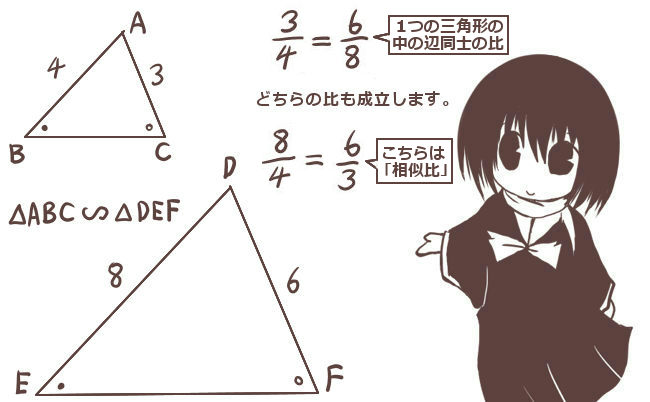
「形は同じでサイズだけが違う」というイメージをつかむと難しさが消えるでしょう。
辺の長さの関係を丁寧に整理する必要がある場合もある事にだけ注意。

証明問題も含めて、図形問題が得意になるコツはあまり難しく考えない事です。
意味を考えながら図を描いてみましょう。

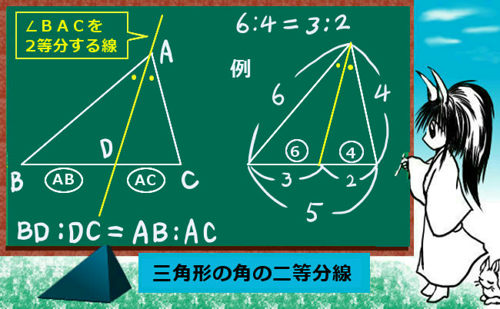
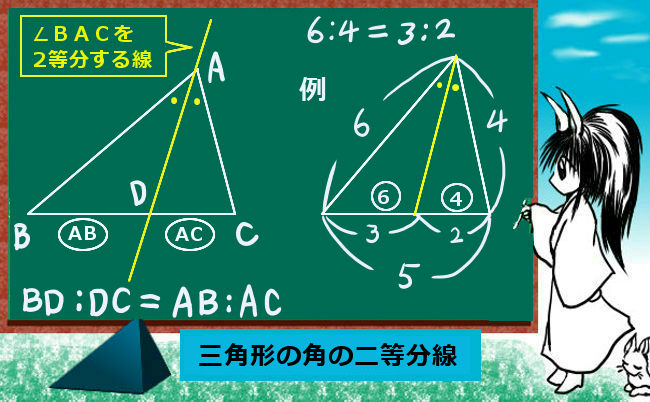
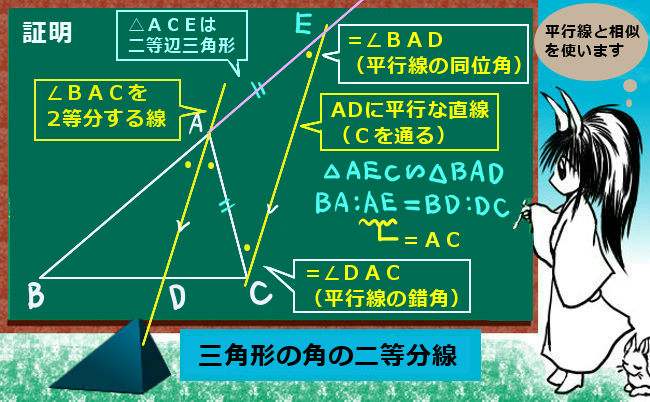
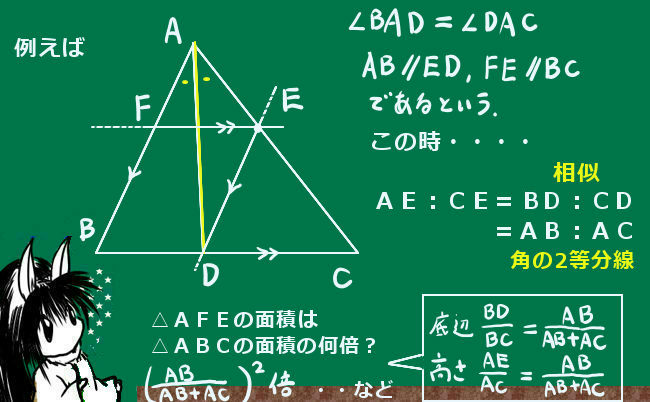
他に図形問題として関連が深いのは角の二等分線と三角形の辺の比の関係などで、これは三角形の相似を根拠として成立します。三角形の相似についてじゅうぶん理解していれば、関係式を暗記せずにその場で導出する事も可能なのです。

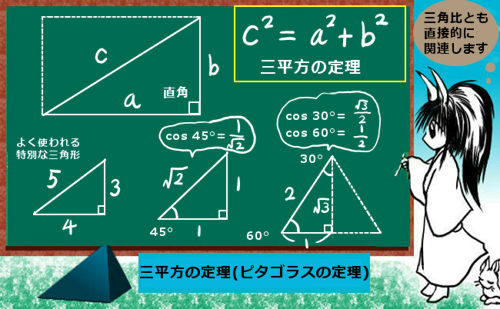
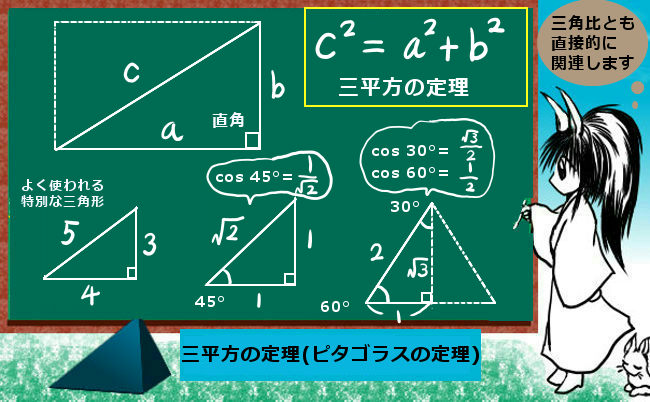
「形」さえ同じであれば、三角形の中の２辺の「比」が一定であるという事は、三角比の考え方の基礎となっています。これは、直角三角形に限定して、特定の角度に対しては２つの辺の長さは一定になる事を利用して決められるものです。高校数学で教えられるものですが、考え方としては三角形の相似の考え方が分かっていれば理解できる内容になります。

群の定義と基本性質

恭平

数学での「群（ぐん）」の定義と基本的性質を説明します。

数学での「群」とはどのようなもの？

まず始めに、数学で「群」（英：group）と呼ばれるものは、具体的なものとしてはじつに初歩的な対象が多く含まれます。

例えば、通常の実数や複素数は、積や和に関して「群」になります。（このように、何らかの演算に関してある集合が群になる・ならないといった表現をします。積について見る場合、０を除く事になります。）

特定の平面図形を「６０°ずつ回転させる」といった操作も「群」としての性質を満たします。これは具体的操作としてはただ三角形や四角形を回してるだけですから、もちろん何ら難しい操作ではありません。他に図形をある軸に対してひっくり返す「鏡映」の操作なども加わる事もあります。

問題は次のようになります：

  • これらに共通する数学的性質は何か？
  • その抽象的な性質を前提にすると、どのような事が言えるのか？

群論ではこれを数学的な視点から整理し、理論を組み立てていく事になります。

「群」の定義

数学での「群」とは、１つの前提条件と、３つの公理を満たす集合を言います。

まず、前提条件として演算が定義される事です。それは、集合Ｇの元【げん】ａ、ｂに対して別の元「ａｂ」が決定するというものであり、このａｂという新しい元もまたＧの元である事が要請されます。群の場合、この演算の事を「積」と呼ぶ事が多いですが、いわゆる加法が該当する場合があります。

前提条件 任意のａ,ｂ ∊ Ｇ　について ａｂ＝ｃ ∊ Ｇ　となる「演算」ａｂが定義できる事。
「群」の定義 「演算」が定義されている前提で、次の３つを満たす集合Ｇを群と呼びます。
  1. 結合律の成立：任意の３つの元ａ,ｂ,ｃ∊Ｇについて、(ａｂ)ｃ＝ａ(ｂｃ)となる。
  2. 単位元の存在：任意の元ａ∊Ｇに対してａｅ＝ｅａ＝ａとなるｅ∊Ｇが存在する。
  3. 逆元の存在：任意の元ａ∊Ｇに対してａａ－１＝ａ－１ａ＝ｅを満たすａ－１∊Ｇが存在。

二番目の条件の単位元は、例えば実数では積に関しては１、和に関しては０が該当します。
三番目の条件の逆元は、例えば実数では２に対する１／２が該当します。（※この時、０では割れないので、積に関しては「０以外の実数」が「群」に当てはまるのです。）

定義
結合律の事は「結合法則」などとも言います。

単位元と逆元以外の一般の交換律ａｂ＝ｂａは、群によって成立するものもあれば成立しないものもあり、成立するものは特に「可換群」と言います。

０を除く実数ｒ、ｓについて、もちろんその積ｒｓは実数であり、ｒ・１＝ｒとなる「１」が存在し、０を除いているので任意の要素についてｒ・(１／ｒ)＝１となる逆元も存在します。よって積に関して「群」である・・という判定をします。
この場合、任意の実数に対してｒｓ＝ｓｒですから、群としては可換群になります。こういった感じで分類をしていくわけです。

他方で、「実数のうち無理数だけからなる集合」は、２の平方根の２乗が有理数になってしまいますから、積に関して群を作らない事になります。

実数が和に関して群を作る事は、ｒ＋ｓは必ず実数、ｒ＋０＝ｒとなる０が単位元として存在する、ｒ＋(－ｒ)＝０となる逆元が必ず存在する、という事から和に関して群である事が分かります。この場合は０を除かないわけです。このタイプの群は特に加群と呼ぶ事があります。

図形を回転させるような操作は、例えば「６０°回転させる操作」をてきとうに文字でおきます。何でもよいのですがギリシャ文字の σ（シグマ）を使う事が多いようです。この時、１２０°回転を σ の２回分の操作とみなして σ２と表したりします。そして、０°回転つまり「何もしない」操作をｅと書く事にします。

そのように定義したうえで、操作 σ自体を要素とみなし、 集合｛ｅ, σ, σ２, σ３,σ４,σ５｝を考えます。すると、この集合はここで定義している操作の「積」に関して群を作るというわけです。この時、σ６＝ｅであるために、任意の２つの要素の積はこの集合の要素に必ずなります。逆元に関しては、例えばσ２に対してはσ４が該当するのです。この例では、操作自体を集合の要素とみなしています。

群の基本性質

さて、数学の理論として群論を考える時には「定義」をしてそれで終わるのではなく、むしろその先が大事です。つまりそのような定義をすると、どのような事が言えるのか・成立するのか？といった事が重要です。

ここでは、定義から直結する性質をいくつか述べます。

単位元の一意性

定義においては、単位元が「存在すればいい」という要請を出しているだけで、これだけではもしかすると「１」に相当する元がもう１つある可能性も匂わせます。しかし、実際はそのような事は起き得ない事を示せるのです。

このような場合、まずｅとｅ’ の２つの単位元を仮定して、ｅ＝ｅ’ を示すというのが１つの常套手段です。

定義から、ｅ’ｅ＝ｅ’です。（ｃｅ＝ｃと同じ理屈です。）

他方、ｅ’も単位元であるのですから、ｅｅ’＝ｅでもあります。
単位元に関しては順序を問わないという定義の要請があるので、ｅｅ’＝ｅ’ｅです。

という事は、ｅ’ｅ＝ｅ’＝ｅを意味します。これで証明終りというわけです。

このような単位元の定義（およびそれを満たすと言える集合）では、必然的にそのような単位元は１つだけ定まるという意味です。

逆元の一意性

では、逆元については一意性は成立するでしょうか？

ａａ－１＝ｅで、これに左側から仮定している別の逆元(ａ－１)’ をかけると、
(ａ－１)'(ａａ－１)＝(ａ－１)’ｅ＝(ａ－１)’
同時に、(ａ－１)’ａ＝ｅにより、(ａ－１)'(ａａ－１)＝((ａ－１)’ａ)ａ－１＝ａ－１
ゆえにａ－１＝(ａ－１)’

よって、上記定義のもとで逆元も一意的に決まるという事です。この計算では、公理の１つめの「結合律」も前提として使用しています。言い換えると、結合律が成立していないと厳密にはこういった計算もできないという事です。

群の逆元の一意性

簡約律

ａｘ＝ａｙ　⇒　ｘ＝ｙ　の事です。

これは単純にａの逆元を左側からかければ終わる話ですが、やはり結合律が成立しているのでそのように計算できるという事が一応重要です。

ａｘ＝ａｙ　⇒　ａ－１(ａｘ)＝ａ－１(ａｙ)　⇔　(ａ－１ａ)ｘ＝(ａ－１ａ)ｙ　⇔　ｘ＝ｙ

積の形の逆元

次のように、積の形全体の逆元は個々の逆元の積になるのですが、順番が逆になるというものです。

(ａｂｃｄ)－１＝ｄ－１ｃ－１ｂ－１ａ－１

これは、
ａｂｃｄ(ｄ－１ｃ－１ｂ－１ａ－１)＝ｅ　かつ　(ｄ－１ｃ－１ｂ－１ａ－１)ａｂｃｄ＝ｅ
である事から示されます。ｄｄ－１＝ｅ、ａａ－１＝ｅなどの関係でどんどん消していけばよいのです。

ただし、交換可能である群の場合は最初の形をひっくり返せる事からこれについては気にしなくていい事になります。実際、実数などでの割り算ではこのような「順番」については気にしなくてよいわけです。

　　　

円の接線と内接・外接

恭平

図形問題としての円に対する接線の考え方と、それとセットになる内接・外接の考え方を説明します。

学校で教わる内容としては中学数学・高校入試の範囲ですが、一部はそれ以降の話にもつながる重要事項も含んでいます。なぜかというと微積分での微分係数は関数をグラフ上で図形的に見た場合の「接線」の傾きだからです。また、高校数学では直線を一次関数とみなして種々の考察をして問題を解かせる場合も多いので、円と関わりを持たせた接線の話は中学校以降でも出てくるのです。

円に対する接線の性質

まず「接線」とは何かと言いますと、
「ぴったりくっつくように１点のみで交点を持つ直線」の事を言います。

また、そのよう形で図形同士が交わる時に「接する」という言葉を使います。「直線 L は円Oに接する、接している」といった具合です。（「接線」は必ず直線を指しますが、「接する」という言葉は曲線同士に対しても使います。例えば円と円が「接する」場合というのもあり得ます。）

図形同士が接する点を、「接点」と言います。

接線と法線

同じ１点で交わる場合でも、突き抜けるように交わる直線は接線とは言わないのです。その場合は単純に、１点で交わる交点です。

「接する」という事は数学的に厳密にはどのような条件を要請する事なのか？という事についてはここで触れないで置きますが、図で見れば分かると思います。中学校の範囲では、見て分かるという程度でじゅうぶんです。それで図形問題は解けるからです。

円に対する接線の重要な性質の１つとして、「接点と中心を通る直線は接線と垂直になる」というものがあります。接点を通り接線に垂直な線を法線と言うので「円に対する法線は中心を必ず通る」とも言えます。

法線

接点を通り、かつ接線に対して垂直である直線の事。
円の場合、法線は必ず円の中心を通ります。

★この事実を使って図形問題を解けと言われるのは中学校と一部高校においてだけでですが、この円に対する接線と法線の性質自体は物理学への応用などでも使ったりします。そのため、内容的には結構重要です。

どういう理由で１つの接点を通る法線は中心を通るのかというと、図形的には次の通りです。

証明の説明図

まず、円周上の２点Ａ、Ｂと円の中心Oからなる三角形は二等辺三角形なので∠AOBが直角になる事はあり得ても、残りの２角は直角にはなり得ません。（三角形の内角の和は１８０°、つまり２直角であるため。）

すると、点Ａに直線が接するには、その直線と線分AOは直角でなければなりません。もし直角でなかったら、その直線上で点Ａ以外にＯまでの距離が等しい点、つまり円周上の点が存在する事になり接線ではなくなってしまいます。

という事は、接線に垂直で接点を通る法線は、接点と中心の両方を通る事になるので題意は示されます。

簡単に言うと、円周上のある点を通る直線は、その点と中心を通る線分に対して垂直である場合に限りその１点のみで交わり、垂直以外の角度の場合には別の円周上の点と必ず交わってしまう（そのような円周上の点が必ず存在する）という事です。

☆この事は、高校数学での図形を式で表す方法でも証明できます。考え方自体は二次方程式の解が重解になる条件を出すだけなので難しくはありません。

内接と外接

また、図形問題でよく取り上げられますが、円に内接する図形、外接する図形というものがあります。ここで、「外接」の場合は特定の図形が必ず円に「接している」事が要求されますが、「内接」の場合は必ずしも接していなくてもよくて頂点などが全て円を突き抜けない形で触れていれば要請を満たします。

図で見ると分かりやすいでしょう。例えば内接三角形と外接三角形の違いを見てみましょう。

内接と外接

円以外の図形側から見た時、言葉の使い方として内接と外接は逆になります。

つまり、円に内接する三角形側から見れば「円は外接」しています。

三角形に対して円が内接していると言う場合は、円に対しては三角形は外接しているのです。

これらの内接・外接の関係は、図形問題として出題される場合には別の事項と組み合わされる事がほとんどです。例えば、円に内接する三角形・四角形は円周角の定理と組み合わせて問われる事が多いです。円に外接する三角形を考える場合には、中心から接点に向けての線分が接線と直角になる事実を使わせる事が多いです。

ひねったパターンだと、角の二等分線の事項も絡めて三角形の面積比などを問う出題もあります。

複雑にしようと思えばいくらでも問題をひねれるのが内接・外接に関する図形問題の厄介なところですが、必要な定理や数学的事実は限られているという事を押さえる事が重要です。前述した事の中で言えば、「円に対する接線がある時、法線は中心を必ず通る」といった事項です。

そういった、限られた数の基礎事項を確実に押さえたうえで、いろいろなパターンの問題を解いてみる事が中学校でのこの分野を攻略する鍵と言えるでしょう。複雑な定理や人があまり知らないような定理を暗記する必要はないのです。

球に関する公式

恭平

球の表面積と体積の公式はセットになっています。微分と積分の関係で結ばれています。
微分の公式と積分の理論については別途に詳しくまとめています。

目次：

  1. 公式
  2. 表面積公式の導出
  3. 体積公式の導出

直接的な問いとして出題されるのは高校数学の範囲ですが、球の表面積や体積を種々の理論で「使う」事は大学数学と物理学でも引き続き行われます。特に物理学で円や球がモデルとしてよく使われますが、これは単純に、半径が等しいと性質が理論を組み立てる際に非常に便利であるからです。

公式

球の表面積と体積の公式は次のようになります。

公式：球の表面積と体積

$$S=4\pi r^2【球の表面積】$$ $$V=\frac{4}{3}\pi r^3【球の体積】$$ ★覚え方としては、面積は２乗、体積は３乗という点は四角形と立方体の関係と同じと考える事ができます。比例係数については微分・積分の関係にあり、円が関わりますから円周率もくっついてくるというわけです。

公式の導出については、じつは
円周の長さ　→　円の面積　→　球の体積　→　球の表面積　という順番です。
しかも、基本的には微分と積分の関係で結ばれているのです。ただし微積分による導出では、順番としては体積が先でその次が表面積という事になります。

体積と表面積

表面積公式の導出

球の体積のほうの公式の「４／３」という係数が不可解で覚えにくいという人もいるかもしれませんが、微積分を考えてみてください。球の体積公式をｒで微分すると球の表面積になるのです。

これはそう考えると単に覚えやすいという事ではなくて、数学の理論としても本質的な事なのです。

$$ｒで微分する：\frac{d}{dr}\left(\frac{4}{3}\pi r^3\right)=4\pi r^2$$

このように、初歩的な微分の公式で体積と表面積の関係が結ばれています。

逆に表面積の公式をｒで積分すれば体積の公式になりますが、これはより正確には「０からｒまで」の定積分になります。しかし０の部分は代入すると消えるので、公式を覚えるという意味では結果的に考えなくてもよい事になります。

面積と体積の公式
円と球についてのこれらの公式は、ｒに関する微積分の関係で結ばれています。

尚、積分を使えば最初に円の「面積」をいきなり出す事も計算上は可能ですが、この計算ではじつは三角関数への置換積分を利用します。そこで三角関数の微分公式を使うわけですが、肝心のこの三角関数の微分公式は、円周率が極限値として存在する事を前提としています。
そのため、この積分による面積計算は円周率という値の存在の「証明」としては、通常は使いません。ただし「理解」する方法としては有用です。また円周率の正確な数値3.14159265・・を直接計算するための手法としては、じつは周の長さよりも円の面積のほうを利用する事が多いのです。

体積公式の導出

しかし、球の体積と表面積が微積分の関係にあるとすれば、平面の円の面積と球の体積はどうつながるのか？という話になります。

微積分の関係である事は同じです。ただし、この場合は [－ｒ,ｒ] の積分区間での定積分になります。また、積分の設定をする際に１つだけ注意が必要です。そのため、定積分の結果である球の体積のほうから円の面積を推測するのは少々難しいでしょう。

基本的には、「断面の面積が分かっている立体」の体積を計算する要領で定積分を行って導出するのです。
直交座標上に立体をおいて、ｘ軸に垂直な断面積をｘで定積分します。

体積の計算

計算を簡単にするため、球の中心を原点におきます。すると、ｘ軸に垂直な部分の断面の円の半径が分かれば、円の面積を－ｒから＋ｒまで積分すれば球の体積となるのです。

その時に、ｘｙ平面の断面で一度考える必要があります。
注意点は、この時の球の、各ｘ座標に対する断面積（円になります）と半径の考え方です。
これは、球をちょうど半分に切った時の円に対するｘ２＋ｙ２＝ｒ２の関係式を踏まえて、
ｘ座標における「ｙの値の絶対値を半径とする」円の面積を断面積として考える必要があるのです。この設定を間違えると正しく計算されないので注意が必要です。

すると、円の式におけるｙの値という事は「平方根が出てきてしまうではないか！」という事になり面倒に思えるかもしれませんが、円の面積はその２乗を考えればよいのですから、ｙ２＝ｒ２－ｘ２だけ分かればじゅうぶんです。

定積分の計算は次のようにします。計算は難しくありませんが、ここでの積分変数はｘであり、ｒは定数扱いという点に少し気を付ける必要があります。

$$\int_{-r}^r\pi y^2dx=\int_{-r}^r\pi (r^2-x^2)dx=\left[r^2x-\frac{1}{3}\pi x^3\right]_{-r}^r$$

$$=r^3-\frac{1}{3}\pi r^3-\left(-r^3-\frac{-r^3}{3}\pi\right)=2r^3-\frac{2}{3}\pi r^3=\frac{4}{3}\pi r^3$$

途中の符号が入り乱れていて分かりにくい場合は、０から＋ｒまで定積分して２倍しても同じです。

$$2\int_0^r\pi y^2dx=2\int_0^r\pi (r^2-x^2)dx=2\left[r^2x-\frac{1}{3}\pi x^3\right]_0^r$$

$$=2\left(r^3-\frac{1}{3}\pi r^3\right)=2\cdot\frac{2}{3}\pi r^3=\frac{4}{3}\pi r^3$$

この計算の仕方は球だけではなくて他の任意の立体の体積でも同じ事です。（もちろん、手計算でやる場合は原始関数を計算で出せるならの話ですが。）

物理学や工学の理論で球の表面積や体積を考える時には、特定の力等の大きさの関係と組み合わせて理論が組み立てられます。特に、距離の逆２乗に比例する（２乗に反比例する）関数と表面積の組み合わせは理論上重要な役目を果たす事になります。

円周率の値はなぜ３.１４なの？

恭平

円周率はなぜ３.１４なのか、なぜ「３」ではいけないかの易しい説明です。円や球に対しては「円周率」が常につきまといますが、それについての話をしましょう。

■ そもそも円周率の定義は？　■ 正確な証明の話　

そもそも「円周率」の定義は？


円周率とは、「円の直径と円周の長さの比」の事であり、値は約３.１４です。
直径が１メートルの車輪の円周の長さは、円周率を用いて
１×３.１４＝約３.１４メートルと計算できます。
円周率の正確な値は３．１４１５９２６５・・・という、循環しない無限小数であり、「無理数」です。
【無理数である事は、背理法で示します。円周率に限らず、特定の数が無理数である事を示す方法は基本的には背理法です。】

円周率の特徴
  1. 「円周の長さ」÷「直径」の値の事を円周率と呼ぶ
  2. 任意の円において値は一定であり、3.141592・・・・
  3. 循環しない無限小数であり、無理数である

円周率を使って円の面積も計算できますが、元々は「円周」と直径の比です。
記号は、ギリシャ文字の「パイ」\(\pi\) を使います。

説明図①
正六角形は６つの「正三角形」で構成される事に気付くと、「直径×３」が円周ではなくて正六角形の周の長さである事が簡単に分かります。


この「約３．１４」という半端な数はどこから出てくるのでしょう？
円に内接する正６角形を考えてみてください。
じつは、簡単な計算により、「円の直径×３」は、ちょうど「円に内接する正６角形の周の長さ」なのです。
この事実が、円周率を「約３」と教える事が、数学的に見て決して良いと言えない理由の一つです。

【多角形の円に対する内接・外接の考え方は別途にまとめています。】

★本当に大雑把な計算（例えば１００くらいになるのか、１０００くらいになるのかといった）であれば円周の長さを「大体３」の計算でやってもよいと思いますが、正確な計算にはならない事は踏まえておく必要があるという事です。実際の値よりも小さくなってしまうからです。


次に、円に内接する正１２角形の周の長さを計算してみると、おおよそ、円の直径×3.1058になります。
この「円周率に相当するような定数」は、円に内接する正２４角形の場合は約3.1326、
正４８角形の場合は約3.1393です。正９６角形まで考えると、3.14が出てきます。
じつは、角をもっと増やしていくと、その値は正確な「円周率」の値に限りなく近づくのです。

動画声優担当ステ♪様　http://sute.tabigeinin.com/

この動画は極限値としての円周率の存在証明の記事にも載せています。

正確な証明の話

☆ここから先の内容は高校数学、さらに詳しくはそれ以上の数学の範囲です。

極限値として円周率が確かに存在する事の証明は少し面倒ですが、平面幾何と極限の基礎知識さえ知っていれば証明は可能です。
円に内接する正ｎ角形と、円に外接する正ｎ角形を考えます。
その中で、２つの頂点と円の中心で作られる三角形に注目します。
ここでじつは少し工夫が必要で、ｎに対してｎ＋１ではなく、２ｎを考えます。

説明図②
通常の数学的帰納法だとｎに対してｎ＋１を考えますが、ここでは２ｎを考えます。
それによって、考察はかなり簡単になるのです。


すると、内接する正２ｎ角形の周の長さは
「内接する正ｎ角形の周の長さより必ず大きい事」と、
「外接する正ｎ角形の周の長さよりは必ず小さい事」が、比較的容易に示せるのです。


これは、内接する正ｎ角形の周の長さを数列として見た時、「単調増加で上に有界」である数列になっている事を示しています。
そして、そのような数列は必ず極限値を持つという定理があるので、
円に内接する正ｎ角形の周の長さは「ｎを無限大にした時に極限値を持つ」事が示されます。


同様に、円に外接する正ｎ角形の周の長さも極限値を持つ事が示せます。
ここで、証明の中で導出している関係式の一つを用いると、２つの極限値は
一致する事を示せます。その値が、円周率と呼ばれる定数です。

円周の長さが直径と円周率の積で表されるという事実は、三角関数の微分公式が成立する根拠でもあるので、理論上、かなり重要な位置にあると言えます。

★三角関数の微分公式の導出には sin x ＜ x ＜ tan x という不等式を用います。
これは実質的には、「内接正ｎ角形の周の長さ＜円周の長さ【極限値】＜外接正ｎ角形の周の長さ」という関係式と同等です。
円周や円弧の長さは極限値なので、解析学（微積分学）的には本来は多少詳しい考察や証明が必要になるというわけです。

サイト内関連記事【円に関する数学】

円周角の定理

恭平

円周角の定理とは、円の１つの弧に対する円周角の大きさは必ず等しく、しかも中心角の半分の大きさであるというものです。言葉よりも図で見ると分かりやすいでしょう。

この定理は、高校入試（特に公立）では非常に出題頻度が高いものです。しかし逆に高校数学では重要度が減り、大学数学や物理学では基本的には使わないと言ってもよいほどその重要度が下がります。

これは、高校数学以降の話では「円に内接する三角形」よりも「円その物」のほうが対象とする図形として重要である事が大きく関わっていると思います。そのため、円周角の定理とは中学数学というか「円に内接する三角形」という話に限定する範囲においては重要な定理である、という位置付けで理解するとよいかもしれません。

定理の内容と意味

まず、「円周角」とは、円に内接する三角形の１つの角の事で、「その対辺を弦とする円弧のうち長い方（優弧）」に着目して呼ばれるものです。例えば「円弧ＡＢに対する円周角」のように使われます。図で見ましょう。一目で分かると思います。

また、「中心角」とは、ある円弧の弦の両端の点のそれぞれと円の中心を結ぶ線分によって構成される角の事です。これも、図を見ましょう。

定理の内容

円周角の定理の内容は、１つの円弧が固定されている時、その円弧に対する任意の円周角の大きさは等しく、しかもその円弧に対する中心角の大きさの半分であるというものです。

円周角の定理

円周上に異なる２点ＡＢがあり、円の中心をＯとすると次の２つの事が成立します：

  1. 優弧ＡＢ上のＡ、Ｂとは異なる任意の点Ｃに対し、
    円周角∠ＡＣＢの大きさは互いに等しい。
  2. ２∠ＡＣＢ＝∠ＡＯＢが成立する。

尚、円弧のうち短い方（劣弧）側の弦と結んでできる角も、大きさは互いに必ず等しくなります。ただし中心角との大きさの関係は２：１にはなりません。（中心角の半分を１８０°から引いた大きさになります。）

高校入試を含めて中学数学では、円周角に関する問いは三角形の相似・合同・面積比に関する事項と組み合わされる事が圧倒的に多いです。

また、円周角が直角になる場合とその条件に関しても好まれて出題がなされる傾向があるようです。

「円周角の大きさは必ず中心角の大きさの半分である」という事が定理の主張の１つですが、これを円弧が半円の場合・弦が直径の場合に適用すると円周角は必ず直角であるという事です。

これは、半円の弧の両端を直線で結ぶと必ず円の中心を通るので中心角＝１８０°とみなせる事によります。すると、その円周角はその半分の大きさで９０°つまり直角になるというわけです。後述するように証明する時にはこの事項自体を場合分けで示す必要がありますが、理屈はじつに簡単です。）

証明

円に内接する三角形が内部に中心を含むかそうでないかで場合分けします。

①内接三角形が内部に円の中心を含む場合

円に対する内接三角形が内部に円の中心を含む時、まず最初に分かるのがじつは「円周角は中心角の半分」というほうの事実です。

これは、内接三角形の１つの辺の両端と円の中心で構成される三角形が、必ず二等辺三角形になる事によるのです。

そして、１つの円弧を固定する時、もう１つの円周上の点を動かしても中心角は同じである事に注意します。これは、この条件のもとで１つの円弧に対する任意の円周角は必ず等しい事を意味し、円周角の定理の主張そのものです。

下図で言うと、次のようになります：

$$(180°-2\alpha)+(180°-2\beta)+(180°-2\gamma)=360°\Leftrightarrow 180°-2\alpha=2\beta+2\gamma$$

$$\Leftrightarrow 180°-2\alpha=2(\beta+\gamma)$$

最後の式は「中心角＝円周角の２倍」を表しています。これはこの条件下で点ＡとＢを固定しておけば、点Ｃが移動しても \(\alpha\) の値は変わらないので円周角の定理の内容が成立するのです。

証明の説明図
いずれの場合でも、半径を２辺とする二等辺三角形を３つ考える事が証明のポイントです。

②内接三角形が内部に円の中心を含む場合

次に、内接三角形が内部に円の中心を含まない場合です。この時も、中心角を構成する二等辺三角形をもとにして証明をします。この場合においても二等辺三角形を３つ作ります。

じつは相似関係などを使う必要は特になく、
「三角形の内角の和は１８０°」「四角形の内角の和は３６０°」という、より初歩的な事実関係だけでじゅうぶんなのです。

図で言うと、中心角は \(180°-2\alpha\) で、そこと隣り合う二等辺三角形の中心角に相当する角は \(180°-2\beta\) です。これらを合わせると、\(360°-2\alpha-2\beta\) となります。

しかし、その角度はよく見ると \(180°-2\gamma\) に等しいのです。よって、次の関係が成立しています。

$$180°-2\gamma=360°-2\alpha-2\beta\Leftrightarrow 2(\beta -\gamma)=180°-2\alpha$$

ここで、式に出てくる \(\beta -\gamma\) は何かというと、これはじつは図の円弧ＡＢの円周角です。つまり、この場合でも「中心角＝円周角の２倍」が成立します。

そして、上記２つの場合において点ＡとＢは固定したままでよいという事に注意しましょう。移動するのは、円周角をなす点Ｃだけなのです。中心角は変化しません。という事は、上記２つの場合の円周角は、いずれも中心角の大きさの半分であり、ともに一致するのです。

ゆえに、内接三角形が円の中心を内部に含むかどうかは気にしなくてよい（その事が示された）という事です。

③内接三角形の１辺上に円の中心がある場合

さて、このように場合分けすると、「だったら三角形の１つの辺が『中心を通る場合』も考えなければだめではないか？」という話になります。実際その通りです。

ただし、この第３の場合が、じつは最も簡単なのです。

直径に対する円周角

円周角をつくる頂点から中心に向かって線分を引きます。すると、二等辺三角形が２つできます。ここで、円周角をなす頂点と直径からなる三角形は、２つの二等辺三角形の角だけから構成されるのです。

すると、三角形の内角の和が１８０°である事から、この場合の円周角の大きさは９０°である事が分かるという計算です。

それゆえ、このような場合でも定理の内容は成立しているので、上記２つの場合と合わせてまとめてよいという事になります。

関連事項：円に内接する四角形

同じく中学数学と高校入試で問われる内容として、
「円に内接する四角形の対角線上で向かい合う角の和は１８０°である」というものがあります。

この理由については、円周角の定理を使うとすぐに分かります。

図のように、補助線として対角線を引きます。この時、内接四角形の１つの角が２つの部分から構成されていると考えます。図で言うと ｘとｙで表しています。

$$\alpha=x+yとおきます。$$

円に内接する四角形

それらｘとｙについて、それぞれ異なる円周角であるとみなす事ができるので、それぞれについて定理を適用します。すると、対角線上で向かい合う内接四角形の角の大きさは、１８０°－（ｘ＋ｙ）という事になります。（「三角形の内角の和は１８０°」を使用。）

しかし \(\alpha=x+y\) でしたから、\(\alpha+180°-(x+y)=\alpha+180°-\alpha =180°\) です。これで題意は示された事になります。

円周角の定理は、高校数学での正弦定理を証明するために使われたりもします。

コーシーの積分定理

恭平

複素関数論の積分の理論における、コーシーの積分定理と、コーシーの積分公式について述べます。両者は名称が似ていて実際極めて近い関係にありますが、式の内容と使い方が少しだけ違うので名称が微妙に分けられているのです。

複素関数の微分、複素関数の積分の基本的な考え方は別途にまとめています。

■ 定理の内容　■ 証明　■ コーシーの積分公式　

定理の内容

コーシーの積分定理とは、積分経路が閉曲線である場合に成立する次の関係式です。

コーシーの積分定理

閉曲線Ｃで囲まれた領域内でｆ(ｚ)が正則である時、$$\int_Cf(z)dz=0$$ ☆ここで、「領域内」とはＣ上の点も含むものとします。

この定理が適用できる条件として領域内で正則であるという事がじつは重要で、１点でも正則でない部分があれば適用はできないのです。

正則でない・・実質的には「微分可能でない」という点は、多くの場合は分母が０になって関数自体定義できないパターンです。しかし、そのような正則でない点が有限個の場合などは、その周囲だけを除いてあげた領域を考えてコーシーの積分定理を適用できたりしいます。その考え方は後述する「コーシーの積分公式」に深く関わります。

しかしこの公式が確かに成立すると分かった時点で、あとは比較的速やかに話が進むのです。

積分定理と積分公式の違い
コーシーの「積分定理」と「積分公式」は一応違うものなので注意しましょう。

定理の証明

複素数の積分については「積分経路を閉曲線にとった場合」には次の式が成立します。

グリーンの公式

$$\int_Cf(z)dz=\int\int_D\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)f(x,y)dxdy$$

グリーンの公式
「グリーンの公式」は、コーシーの積分定理に直結するという意味で重要な公式です。

このグリーンの公式が成立する根拠については、別途に詳しく述べています。積分の経路が閉曲線であるという事がポイントです。複素関数論の初歩の中で、ここが一番難しい・理解しにくいという人も多いのではないかと思います。

グリーンの公式が成立するという条件のもとでは、「コーシーの積分定理」の証明はそれほど難しくはないのです。

グリーンの公式において、関数ｆ(ｚ)が「正則である」という条件をつけます。これは、大雑把には領域内の任意の点で微分可能であるという感覚です。

この時には、グリーンの公式に加えて、複素数の微分のほうについて「コーシー・リーマンの関係式」が成立します。ｆ(ｚ)＝ｕ(ｘ,ｙ)＋ i ｖ(ｘ,ｙ)とした時の、ｕとｖに対する偏微分についての関係式です。

これを使う：コーシー・リーマンの関係式

$$f(z)=u(x,y)+iv(x,y)が正則である時、\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y},かつ\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$$

グリーンの公式の積分の中身を、ｕとｖで表してみます。

$$\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)f(x,y)=\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)(u+iv)$$

$$=i\frac{\partial u}{\partial x}-\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}-i\frac{\partial v}{\partial y}$$

$$=-\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)+i\left(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\right)$$

こういうふうになるので、経路Ｃが閉曲線でｆ(ｚ)が正則という条件なら、関数と経路の形によらず定積分の「積分の中身」の値がうまい具合に必ずゼロになるので、定積分の値もゼロになるという事です。

$$f(z)が正則ならば\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)f(x,y)=-\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)+i\left(\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y}\right)=0$$

$$したがって、f(z)が正則ならば\int_Cf(z)dz=\int\int_D\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)f(x,y)dxdy【証明終り】$$

この定理は、別に魔法によって不思議に成り立つのではなくて「積分経路Ｃが閉曲線で領域内でｆ(ｚ)が正則」という、言ってみれば特殊な条件を課して限定する事によって成立するのです。

コーシーの積分公式

もう１つ重要なものとして、名称が少し紛らわしいのですが「コーシーの積分公式」というものがあります。これは、コーシーの「積分定理」のほうから導出されるものです。

コーシーの積分公式

$$f(z)=\frac{1}{2\pi i}\int_C\frac{f(\zeta)}{\zeta-z}d\zeta$$ この公式の積分の中身の中のｚは、積分変数に対しては定数扱いであり、積分変数（複素数）としては「ゼータ」を文字として使っています。
この関係式の詳細について、次に述べていきましょう。

考え方

コーシーの「積分定理」が適用できる複素関数と領域があったとします。そこで、領域内のてきとうな複素数ｚ＝ｗを考えて、関数をｚ－ｗで割ります。

$$\frac{f(z)}{z-w}を考えます。$$

ｆ(ｚ)が微分可能なら、それをｚ－ｗで割った関数も微分可能です。

ただし、ｚ＝ｗを除きます。

ｚ＝ｗにおいては、関数が定義されないので、当然微分不可能というわけです。
このように、わざと「微分不可能で正則でない点」を考えて、関数にくっつけているのです。

こういう場合に積分はどう考えるのかというと、もとの積分経路に、ｚ＝ｗを囲む（小さな）円を経路として付け足した別の経路を考えてみるのです。なぜ「円」を考えるのかというと、これは閉曲線の中では最も計算しやすいためです。

その円周の経路をＣ１としましょう。もとの経路をＣとし、合わせた経路をＣ＋Ｃ１とここでは書く事にします。積分する時には、次のように経路ごとに項を分ける事ができます。

このとき、小円の経路Ｃ１はその円に関して言えば時計回りに積分が行われています。つまり、小円の経路だけで定積分を考えた場合、本来の符号とは逆であり、そのためマイナス符号をつけます。

$$\int_{C+C1}\frac{f(z)}{z-w}dz=\int_C\frac{f(z)}{z-w}dz-\int_{C1}\frac{f(z)}{z-w}dz$$

ここで、経路Ｃ＋Ｃ１に対してコーシーの積分定理を使います。
（その領域においてｚ＝ｗは除外されていて、含まれていない事に注意します。）

$$0=\int_C\frac{f(z)}{z-w}dz-\int_{C1}\frac{f(z)}{x-w}dz\Leftrightarrow \int_C\frac{f(z)}{z-w}dz=\int_{C1}\frac{f(z)}{x-w}dz$$

ここで、小円の経路Ｃ１のほうについて、ｚ＝ｗ＋ｒeiθと置きます。これは、ｚ＝ｗを中心とした円周上の点を媒介変数表示したものです。ｒは何かてきとうな（小さい）実数であり、媒介変数はθです。

このとき、ｚ－ｗ＝ｒeiθですから、分母が簡単になるという１つのカラクリがあります。変数変換をしていますので微分も必要になりますが、この場合指数関数の微分ですから計算は容易なのです。

$$\frac{dz}{d\theta}=rie^{i\theta}と合わせて、\int_{C1}\frac{f(z)}{x-w}dz=\int_0^{2\pi}\frac{f(w+re^{i\theta})}{re^{i\theta}}\frac{dz}{d\theta}d\theta$$

$$=\int_0^{2\pi}\frac{f(w+re^{i\theta})}{re^{i\theta}}rie^{i\theta}d\theta =\int_0^{2\pi}if(w+re^{i\theta})d\theta$$

このように上手い具合に分母と、変数変換による微分の項が打ち消して消えます。

ここでｒ→０の極限を考えます。すると、f(ｗ＋ｒeiθ) → ｆ(ｗ)です。（これは、より厳密には上限で上から抑える不等式で示します。）

すると、次のようになるような、じゅうぶん小さいｒを必ず考える事ができるという事です。

$$\int_{C1}\frac{f(z)}{x-w}dz=i\int_0^{2\pi}f(w)d\theta=if(w)\left[\hspace{3pt}\theta \hspace{3pt}\right]_0^{2\pi}=i(2\pi-0)f(w)=2\pi if(w)$$

定積分の計算の最後のところは、ｆ(ｗ)が（θに関して）定数であるのでこのようにできるという事です。

整理しますと、結局次のように言えます。

$$\int_C\frac{f(z)}{z-w}dz=2\pi if(w)\Leftrightarrow f(w)=\frac{1}{2\pi i}\int_C\frac{f(z)}{z-w}dz$$

ここで、もとの閉曲線Ｃで囲まれた領域内の点ｗは、何か特別な点ではなく、領域内の任意の点でよかったわけです。ｗを変数ｚに置き換えて、積分の中の変数を何か別のてきとうなものを使っても同じ意味になります。このように、領域内の任意の複素数ｚにおけるｆ(ｚ)を積分で表したものがコーシーの「積分公式」です。

改めてコーシーの積分公式

$$f(z)=\frac{1}{2\pi i}\int_C\frac{f(\zeta)}{\zeta-z}d\zeta$$ この公式の積分の中身の中のｚは、積分変数に対しては定数扱いです。
また、上記の「コーシーの積分定理」との違いに注意してみてください。「コーシーの積分公式」は、複素関数の値自体を積分で表す公式です。

積分の中の変数の記号は別に何を使ってもよいのですが、「複素数の」変数である事を強調するためにギリシャ文字の「ゼータ」を使う事が多いようです。ここでもその表記を使っています。ｔなどを使っても別によいのですが、これは媒介変数として実数の変数を表す事が多いので、積分変数としてゼータを使用する事は、なるべく誤解を避けるための習慣であろうかと思います。

複素数の微積分の理論はこの先も続いていきますが、初歩的な理論としてはここまで理解していればそれほど難解な理論は少ないと思います。

三平方の定理およびその逆【証明】

恭平

三平方の定理は平面の直角三角形の辺の長さに関して成立する関係式です。（曲面に対して拡張したものも存在します。）別名をピタゴラスの定理とも言います。

目次：

  1. 定理の内容
  2. 証明
  3. 定理の「逆」も成立する
  4. 他の分野との関連

中学で教わる数学公式の中でも重要度が高いものの１つだと思います。

定理の内容

直角三角形の斜辺の長さの２乗は、残りの２つの辺のそれぞれの２乗の合計に等しいというのが三平方の定理の内容です。「平方（つまり２乗）」が３つある事が「三平方」の意味です。

図による説明
三平方の定理

直角三角形の斜辺の長さをｃ、残りの辺の長さをそれぞれａ、ｂとすると次の関係が必ず成立する：$$c^2=a^2+b^2$$

これは一般の鋭角三角形、鈍角三角形も含めた余弦定理の特別な場合です。
【余弦定理は、普通は高校数学で学習します。】

余弦定理の特別な場合が三平方の定理

$$c^2=a^2+b^2 -2ab\cos \theta$$ θ＝９０°の時 cosθ＝０であり、余弦定理は三平方の定理に一致します。
ただし、余弦定理の証明には三平方の定理が必要です。

具体的な適用例としては、直角を挟む２辺がそれぞれ３、４である直角三角形の斜辺の長さは５になります。

３２＋４２＝２５＝５２　という計算になるわけです。

また、１つの角度が４５°、６０°といった特別な三角形の斜辺の長さの計算にも三平方の定理を使います。

１つの角度が４５°の場合・・２つの辺の長さがそれぞれ１の時、
１２＋１２＝２　より、斜辺の長さは\(\sqrt{2}\)

１つの角度が６０°の直角三角形の場合は、２つ合わせると正三角形になる事を組み合わせて、斜辺と１つの辺から、もう１つの辺の長さを三平方の定理で計算するという流れになります。

$$c^2=a^2+b^2\Leftrightarrow b^2=c^2-a^2\hspace{5pt}の関係を使います。$$

斜辺の長さを２とすると、もう１つの辺の長さは１であるので、残る１辺の長さは\(\sqrt{2^2-1^2}=\sqrt{3}\)

ちなみにこれが三角比・三角関数における、角度が特別な時の値の正弦や余弦の意味に直接関連します。

$$ \cos 45°=\frac{1}{\sqrt{2}}$$

$$\cos 60°=\frac{1}{2},\hspace{10pt}\cos 30°=\frac{\sqrt{3}}{2}$$

証明

証明の方法は１つではなく複数ありますがここでは２つ紹介します。

※上記でも触れた余弦定理の証明には三平方の定理が必要なので、余弦定理の特別な場合として三平方の定理が成立するという事は、証明としては使用できないのです。

①三角形の相似関係を使う方法

この方法は、直角三角形の中には別の小さな直角三角形が必ずある事に注目して、三角形の相似関係から辺の長さを計算すると三平方の定理の内容が得られるというものです。

三角形の相似を使う方法は、アインシュタインが１２歳ほどの時に自ら証明したと、のちに語ったと言われているものです。これは、彼が「発見」したというよりは、どのように証明ができるのか自ら考え、自力で見出す事ができてとても嬉しかった、というエピソードですね。彼曰く、謙遜してかもしれませんが「苦労」したとのことです。

まず、直角の部分の頂点から、斜辺に向けて垂線を引きます。その垂線の足で斜辺の長さを分割するのです。

図のように長さを変数でおき、三角形の相似関係で式を組み立てます。

相似関係を使う証明

ｃ＝（ｃ－ｈ）＋ｈ　となるように辺ＡＢを分割します。
∠ＡＨＣ＝∠ＢＨＣ＝９０°となるようにします。（そのようにできる点Ｈが必ずＡＢ上に存在。）

この時、もとの三角形と相似関係にある小さな三角形は２つある事がポイントです。
すると、三角形の相似関係により辺同士の長さの比は次のようになります。

$$\frac{c}{a}=\frac{a}{c-h}\Leftrightarrow c^2-ch=a^2$$

$$\frac{c}{b}=\frac{b}{h}\Leftrightarrow ch=b^2$$

$$２式を合わせると、c^2-b^2=a^2\Leftrightarrow c^2=a^2+b^2【証明終り】$$

どの辺がどの辺に対応するか分かりにくい場合には、図のように相似関係が明らかに成立すると分かるように図を描き直して整理すると見やすいと思います。

②三角形の合同関係と面積を使う方法

この方法はユークリッドの『原論』における証明方法として古くから知られ、３つの「平方」とは正方形の面積であるという考え方によります。（※「ピタゴラス」によるものではないのです。）

直角三角形の各辺を1辺とする正方形を３つ作り、三角形の合同関係から斜辺の長さの正方形の面積は、残る２つの正方形の面積の合計に確かに等しい事を示せるのです。

補助線を１本引きますが、じつはこれは上記の相似関係で使ったものと同じです。ただしこちらの証明では、補助線は斜辺を突き抜けて正方形のもう１辺にまで伸ばす事になります。

ユークリッドによる証明

合同関係は、図で言うと△ＡＡ’Ｃと△ＡＢＣ’について成立します。合同という事は面積も等しい事がポイントで、図をよく見ると、この細長い三角形の面積は正方形の半分、つまりｂ２÷２です。底辺、高さともに長さはｂであることによります。

合同条件は「２辺とそのはさむ角が等しい」です。
図で言うと次のようになります。
ＡＣ＝ＡＣ’　ＡＡ’＝ＡＢ　∠ＣＡＡ’＝∠Ｃ’ＡＢ＝９０°＋∠ＢＡＣ　となります。

同様に、図の△ＢＢ’Ｃと△ＢＢ”Ａについても合同関係が成立し、こちらの面積はａ２÷２です。

ここで、補助線によって分割される大きな四角形の長方形部分の面積は、細長い三角形の面積の２倍である事に注目します。（底辺と高さの値が三角形のものと等しいため。）

長方形の面積の合計は正方形の面積ｃ２に等しいですから、ｃ２＝ａ２＋ｂ２が成立するというわけです。

証明の補助図
こちらは証明の補足です。四角形と細長い三角形の面積は一見すると共通点があるようには見えないかもしれませんが、底辺と高さを考えると確かに三角形と四角形の面積比は１：２になっています。

定理の「逆」も成立する

上記での証明は、正確には次の命題の証明になっています：
三角形の斜辺の長さがｃ、残りの２辺の長さがａ、ｂのもとで
三角形ＡＢＣは直角三角形　⇒　ｃ２＝ａ２＋ｂ２

では逆に、
ｃ２＝ａ２＋ｂ２　⇒　三角形ＡＢＣは直角三角形
という命題は成立するのかというと、じつは成立します。

この証明は次のようにします。（これもユークリッドの方法です。）

ｃ２＝ａ２＋ｂ２　が成立している三角形と１辺を共有する直角三角形を考えます。この直角三角形の１つの辺は、もとの三角形の別の１辺と同じ長さのものを考える事が必ず可能です。

この時点で、最初の三角形と別途に作った直角三角形は、２つの辺の長さが等しいわけです。

ここで、
命題：三角形ＡＢＣは直角三角形　⇒　ｃ２＝ａ２＋ｂ２は直角三角形
は上述の証明方法により真であると言えますから、新しく作った直角三角形についてこれを適用できます。

すると、２つの三角形は２辺が等しいですから、辺の長さについて「三平方」の関係がともに成立する条件になるので、残りの１辺の長さも等しくなるのです。

これによって、もとの三角形は新しく作った直角三角形と合同です。（合同条件は『３組の辺の長さがそれぞれ等しい』。）という事は、もとの三角形も直角三角形であるという事です。もちろん、斜辺に対応する角が直角になります。

よって、命題：ｃ２＝ａ２＋ｂ２　⇒　三角形ＡＢＣは直角三角形
も成立しますから、三平方の定理は「必要十分条件」の形という事になるのです。

三平方の定理は「必要十分条件」である事を明示する場合

三角形の斜辺の長さがｃ、残りの２辺の長さがａ、ｂのもとで
三角形ＡＢＣは直角三角形　⇔　ｃ２＝ａ２＋ｂ２

他の分野との関連

上記で三角比および三角関数との関連に少し触れましたが、他の数学的事項や物理学・種々の工学とも密接に関連します。

三平方の定理は様々な場面で「距離」を計算する計算のツールとして使われます。直交座標を考えた時、斜めの線の長さは２点間の距離になります。この時、座標さえ分かっていれば三平方の定理から距離を必ず計算できるというわけです。

この「距離」という考え方はもちろん理論の中だけではなくて現実の距離の計算にも適用できるので、物理学でもじつに頻繁に使用され、また測量のような、より実務的な事項にも間接的に利用されます。

数学の図形的な平面幾何以外の分野でも、ベクトルや複素数の理論において三平方の定理をもとに定義が成されます。ベクトルの「大きさ」や複素数の「絶対値」の考え方自体は、三平方の定理そのものです。

$$\overrightarrow{X}=(x,y)のとき、|\overrightarrow{X}|^2=x^2+y^2$$

$$z=x+iyのとき、|z|^2=x^2+y^2$$

三平方の定理の考え方は、直交座標、複素数、ベクトル、物理学、測量と、幅広く計算に使われます。

上記で少しアインシュタインに関するエピソードを紹介しましたが、彼の特殊相対性理論の考察においても三平方の定理は使用され、一般相対性理論では平面ではなくて曲面（４次元）において三平方の定理を拡張した考え方の一部が使用されています。なお、平面から曲面に拡張を行ったときには必ずしも「三平方」ではなくなってしまうので、その観点から「ピタゴラスの定理」のほうの名称を優先して使うべきではという考え方をする人もいます。

４次方程式の解の公式

恭平

４次方程式の「解の公式」の導出方法を説明します。

公式の導出の流れ

３次方程式同様に公式自体は複雑で、理論の中ですらあまり計算の役に立ちません。そのため覚える事は一般に不要ですが、４解を必ず「係数のベキ根で表せる」という事が数学的な事実として重要な位置付けなのです。「４次」までは方程式の係数を使った解の公式が存在するという事です。

解法の手順は多少３次方程式の場合に似ていて、いくつかのステップを経て下位の次数の方程式に変形できる事が、公式を導出できる根拠になります。

  1. 方程式の各項を左右の辺に分けて平方の形を作る事を考える
  2. 方程式の解とは別の未知数ｙを考え、加える事で「平方＝平方」の形になるｙの条件を考える
  3. 結果：ｙは３次方程式の解になり、もとの方程式の係数のベキ根の組み合わせで書く事ができる。よって、もとの方程式の解ｘを表す「公式」を得る。

公式の導出

４次と３次の項と、その他の項を両辺に分けます。

$$x^4+ax^3+bx^2+cx+d=0$$

$$\Leftrightarrow x^4+ax^3=-(bx^2+cx+d)$$

左辺を平方の形にする事を考えます。そのために、両辺に２次の項を加えるのです。

４次方程式の解の公式の導出①

$$両辺に\frac{ax^2}{4}を加えます。$$

$$x^4+ax^3+\frac{ax^2}{4}=-(bx^2+cx+d)+\frac{ax^2}{4}$$

$$\Leftrightarrow \left(x^2+\frac{ax}{2}\right)^2=\left(\frac{ax^2}{4}-b\right)x^2-cx-d$$

右辺は２次式なので、何かの項を加えれば強引に平方の形にできます。
しかし、ここでは左辺も平方の形である事を保ちたいのです。そのため、少々工夫をします。

今のこの状態で左辺は平方の形である事がポイントで、ある別の未知数ｙを使った次の項を両辺に加えます。

$$\left(x^2+\frac{ax}{2}\right)y+\frac{y^2}{4}を両辺に加えます。$$

$$\left(x^2+\frac{ax}{2}\right)^2+\left(x^2+\frac{ax}{2}\right)y+\frac{y^2}{4}=\left(\frac{ax^2}{4}-b\right)x^2-cx-d+\left(x^2+\frac{ax}{2}\right)y+\frac{y^2}{4}$$

$$\Leftrightarrow \left(x^2+\frac{ax}{2}+\frac{y}{2}\right)^2=\left(\frac{ax^2}{4}-b+y\right)x^2+\left(\frac{ay}{2}-c\right)x+\frac{y^2}{4}-d$$

左辺は再び平方の形であり、右辺はｙという未知数を含んだ２次式です。

ｙという数を加える前との違いは、それを加える前の各係数は所定の（任意の）係数ですので値を自由にいじれませんが、ｙというのは変数であるこの段階では任意ですので調整がきくという事です。次に問題となっていくのは、右辺を平方の形するためのｙを、「もとの方程式の係数ａ、ｂ、ｃで表せるか？」という事です。

４次方程式の解の公式の導出②

この段階で、右辺を平方の形にする事を考えましょう。これは、一般の２次関数をそのような形にするのと全く同じ要領です。式の形だけが多少込み入るので、右辺の式の係数をそれぞれＡ，Ｂ、Ｃと置いておきます。

$$右辺＝Ax^2+Bx+Cと置きます。$$

$$Ax^2+Bx+C=A\left(x+\frac{B}{2A}\right)^2-\frac{B^2}{4A}+C=0$$

$$よって、-\frac{B^2}{4A}+C=0\Leftrightarrow B^2-4AC=0となればよい。$$

この計算自体は、２次関数や２次方程式をいじくる時のものと全く同じですね。ここで、Ａ，Ｂ、Ｃをもとの形に戻して必要な条件を眺めてみましょう。

$$B^2-4AC=0\Leftrightarrow \left(\frac{ay}{2}-c\right)^2-4\left(\frac{ax^2}{4}-b+y\right)\left(\frac{y^2}{4}-d\right)=0$$

これが成立すればよいのですが、これを満たすｙが存在するかという話です。式をよく見ると、これはｙに関する３次方程式で、しかも係数はもとの４次方程式の係数ａ、ｂ、ｃの組み合わせで構成されている事がポイントです。３次方程式ですから、これは「解の公式」が存在しますからｙに関して解く事ができて、しかももとの４次方程式の係数ａ、ｂ、ｃで表す事ができるのです。

その条件をｙが満たすものとすると、もとの４次方程式は「平方＝平方」の形になりますから、これは２乗の形をはずす事ができます。その時に、もちろん正負の２つの外し方があります。

$$\left(x^2+\frac{ax}{2}+\frac{y}{2}\right)^2=A\left(x+\frac{B}{2A}\right)^2$$

$$\Leftrightarrow x^2+\frac{ax}{2}+\frac{y}{2}=\pm \sqrt{A}\left(x+\frac{B}{2A}\right)$$

$$A=\frac{ax^2}{4}-b+y,\hspace{5pt}B=\frac{ay}{2}-c$$

つまり、ｘに関する「２つの２次方程式」ができます。もちろん、これはｘについてさらに解く事ができるのです。また、解の個数は最高で２×２＝４個という事も分かります。すなわち、４次方程式の「解の公式」も方程式の係数を使って表す事ができるという事が示された事を意味します。

ただしこれまでの経緯を見て分かる通り、まずｙに関して３次方程式を解き、その解を係数として組み合わせた２次方程式をさら解くという作業があります。ですので、「４次方程式の解の公式」というのは少なくとも手計算では「使いたくない公式」である事はよく分かるかと思います。

２次方程式の解の公式も決してきれいな形ではないですが、あれはまだ一応手計算で「使える」公式であるという事が対比して分かると言えるかもしれません。

代数学の中での位置付け

さて問題は続き、「では公式の複雑さは度外視して、５次方程式も同じように『解の公式』を出せるのか」という話になります。結論は次の通りです：

  • １～４次方程式と同じ要領で、同じ意味での５次以上の方程式の「解の公式」を構成する事はできない。（それが数学的に正しい答えである）
  • その事を数学的に証明するには、視点を変えたより抽象的な考察が必要である。

言ってみれば、３次方程式や４次方程式の解の公式の導出は、多少計算が複雑だったり工夫が必要だったりするものの、やる事自体は「高校数学」の範囲で理解可能であるものなのです。

他方で、「視点を変えてみた抽象的な考察」というのが、大学以上の授業で言う「代数学」の分野の内容だと捉えればよいと思います。数学史的には、１９世紀以降に西欧で考察されるようになった数学の分野です。

言い換えるとそれは西欧でもその時期になって初めて本格的に研究されるようになった事案であって、言われなければ普通は気付かないし、言われずに気付いたとしても分かりやすい理論として即座にまとめるのは至難の業である事が反映されているように思えます。しかし簡単な事項から少しずつ整理すれば、もちろん誰にでも理解する事は可能です。

三角形の角の二等分線

恭平

三角形の角を二等分する線を引いた時に成立する１つの図形的性質があります。

これは高校入試の図形問題でよく出題され、場合によっては大学入試で部分的に扱われる事もあります。

三角形の角の二等分線に関して成立する関係

△ＡＢＣにおいて線分ＢＣ上に点Ｄがあり、線分ＡＤは∠ＢＡＣを２等分するという。
（つまり∠ＢＡＤ＝∠ＣＡＤとなっている。）
この時、線分の長さの比についてＡＢ：ＡＣ＝ＢＤ：ＣＤが成立する。

まず、三角形の１つの角を二等分する線を引きます。これは、例えば６０°の角度であれば３０°と３０°に分割する線を引くという意味です。

次に、その線が１つの辺とぶつかる交点を考えます。すると、じつはその交点は、他の２辺の長さの「比」でその辺を分割しているのです。こういったものは、図で見たほうが多分分かりやすいでしょう。

三角形の二等分線①
例えばＡＢ＝６、ＡＣ＝４であれば点ＤはＢＣを６：４＝３：２で分割します。ＢＣ＝５であればＢＤ＝３、ＤＣ＝２であると決まるという事です。

これを証明するのは比較的簡単です。次のようにします。
（★ただし、入試の問題を解くという観点からは結果の関係式を確実に覚えておいたほうがよいです。しかし仮に忘れた時でも証明は難しくないという事です。）

まず、二等分する角につながる三角形の辺の１つを延長します。次に、二等分する角の対辺の１端から、角の二等分線に「平行」な直線を引きます。すると三角の相似関係により証明ができるというのが簡単な流れです。この時、二等辺三角形ができる事に気付く事も１つの重要な点です。

三角形の二等分線②（証明）
１つの辺の延長と、補助線として設ける平行線をつなげると大きな１つの三角形ができます。それと元の三角形の相似関係を考え、さらに図の△ＡＣＥが二等辺三角形である事に注目すると関係式が得られるのです。

この関係が中学校の数学、特に高校入試で問われる場合は、単独ではなくて他の図形上の関係と合わせて計算をさせる事が多いと思います。例えば、三角形の相似問題の１つの条件として使われたり、三角形の面積比を計算させるといった具合です。

また、円周角関連の事項と合わせた出題もあり得ます。この手の問題は計算を面倒にさせようと思えばいくらでもそのように問いを作れるので、いくらか練習しておかないといきなり問われた時になかなかうまくいかない事もあろうかと思います。

高校入試などでは三角形の面積比を計算させる問いなどで使わせる例があります。この図の例では、例えば情報としてＡＢ、ＡＣ、ＢＣの長さだけが与えられていて△ＡＥＦと△ＡＢＣの面積比を計算させるといった具合です。

さて、この三角形の二等分線に関する問いは多いですが、中学での勉強を終えて高校での学習に移る時、そんなに使うのかというと正直あまり使わないと思います。ただし、図形の平行・直角・相似・合同といった考え方は引き続き使用される事があります。

そのため、試験問題を解くという事を抜きにして語るのであれば、重要なのは関係式が成立する「理由」のところだと思います。平行線の性質や相似関係によってこのような事が言えるという事が、本当は一番覚えて理解しておきたいところかとは思います。