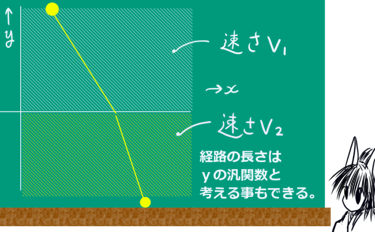
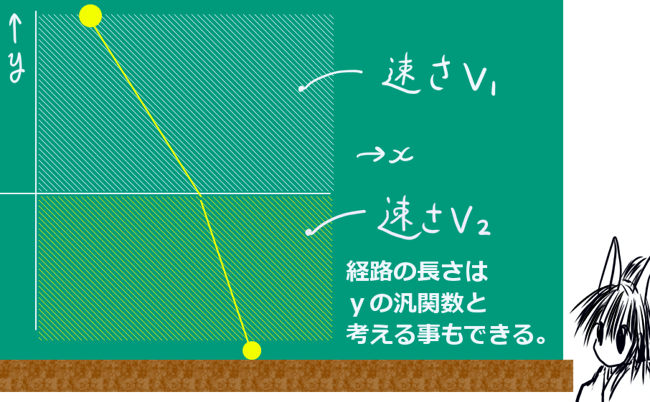
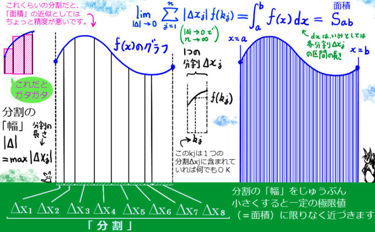
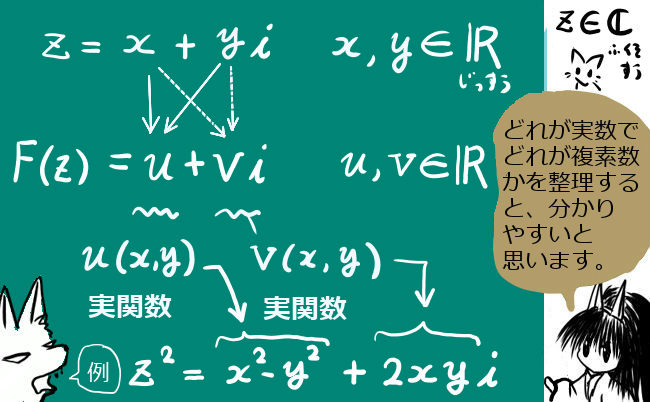ここでは複素関数論におけるグリーンの公式と呼ばれる式について説明します。
同じ名前の公式はいくつもあって大変紛らわしいのですが、ここでは複素関数論の、複素数の積分に関して成立する関係式について述べます。
この公式は、複素関数論で重要なコーシーの積分定理を証明するのに必要です。
複素数の定義と基本事項については別途に詳しくまとめています。
グリーンの公式とは?
■ 公式の内容 ■ 公式の別の表記法 ■ 複素関数論の中での位置付け
公式の内容
複素関数論におけるグリーンの公式とは、次の複素数の積分に関する関係式を言います。
$$ここで、\left(i\frac{\partial}{\partial x}-\frac{\partial}{\partial y}\right)f(x,y)=\left(i\frac{\partial f(x,y)}{\partial x}-\frac{\partial f(x,y)}{\partial y}\right)\hspace{5pt}の事です。$$
また、ここでのxやyでの偏微分は、
これらの変数を「独立変数であるように見なした時の」偏微分の計算を指します。
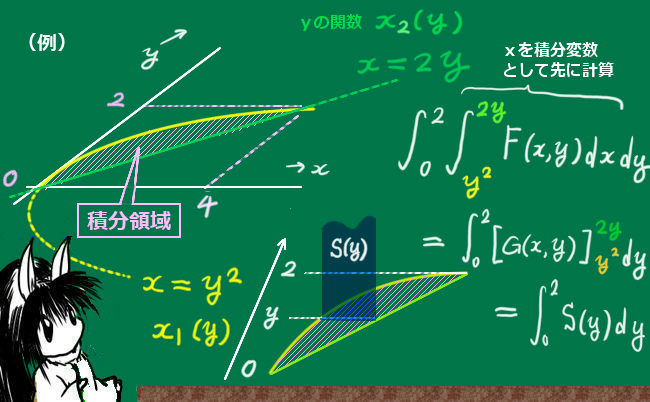
そのように言うのは、ここでは積分の経路として閉曲線を指定しますから、xとyは独立変数ではなく従属関係にあるからです。(例えばy=2xなど。これについてはこのページの後半でも再度触れます。 )
ただし、ここでの偏微分で表される計算は、通常の独立多変数に対する偏微分の時と同じく、「yを固定してxだけで微分操作をする」という意味である・・という事です。

この結果自体が得られると、その後の理論はしばらくの間は割と難しい理屈が少なく進んでいくところがあります。
公式の別の表記法
全く同じ公式を、別の表記で表す事もあります。
これは、形式的には「複素変数zで偏微分する」形で表されますが、じつはこれは普通の意味での偏微分ではなく、複素関数論において特別に定義される記号です。
z=x+iyの時、記号を次のように定義します:
$$\frac{\partial}{\partial \bar{z}}=\frac{1}{2}\left(\frac{\partial}{\partial x}+i\frac{\partial}{\partial y}\right)$$ $$\frac{\partial}{\partial z}=\frac{1}{2}\left(\frac{\partial}{\partial x}-i\frac{\partial}{\partial y}\right)$$この記号を使うと、上記のグリーンの公式は次のように書けます。
どちらの表記法でも問題ないですが、記号の定義を知らないと、「共役複素数で偏微分って何の事・・??」と、思ってしまうかもしれませんね。その記号は、あくまで定義によって特別に意味が約束されているものです。
複素関数論の中での位置付け
冒頭で少し触れていますが複素関数論の複素数の積分論の中で、「コーシーの積分定理」というものがあります。これは、正則関数を閉曲線に沿って定積分すると必ず0になるというもので、これをもとに種々の複素数の積分の理論は組み立てられています。
それで、その積分定理は自明な事かというと、そうではありません。その定理の証明のためにグリーンの公式が使用されます。
ですから複素関数論におけるグリーンの公式とは、言ってみれば理論上重要な定理の「補題」的な位置付けにあると言えると思います。
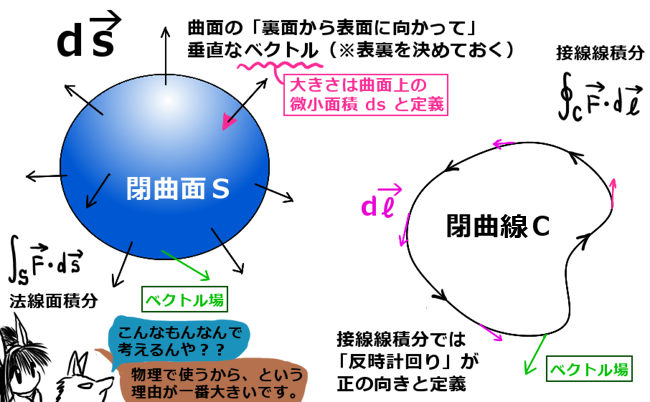
もちろん、必要があれば他の用途に使う事もできます。また、考え方自体は多変数関数の線積分や、ベクトル解析に共通するところがあるのでそれらの分野にも考え方を適用できます。
グリーンの公式の証明
証明のポイント
積分の経路として「閉曲線」考えている事と、定積分を行う場合には複素数の実部と虚部に分けて考えてよい事がポイントです。
公式の内容を見ると、曲線上の積分を領域内の重積分で表せるという事であるわけですが、ある関数はその導関数の定積分として上手く表せる事を利用します。この考え方はベクトル解析での定理の一部を示す時にも使用されます。
考え方はシンプルで、微積分学の基本定理をうまく使います。
定積分を考える時には項が2つ出てきてしまいますが、閉曲線を考えている事がポイントで、上手い具合に閉曲線の「上部分」「下部分」等の2つの部分に分けて必要な項を作れるのです。この時、後述しますがxとyによる積分それぞれについてそれらを考えるので、少なくとも4つの経路を考え、最後に合算します。
証明の後半では重積分の結果は積分変数の順序によらない事も使用します。
積分経路と媒介変数
dz=dx+idy において、閉曲線Cを指定する場合はxとyに従属関係があって、
1つの媒介変数tで表す事ができます。
$$x=x(t),\hspace{5pt}y=y(t)$$

(より一般的には閉曲線ならg(x,y)=0が成立。例えば円や楕円。)
積分する時にはxとyを別々に考える事ができるのであまり気にしなくてもよいのですが、 補足的に、述べておきます。
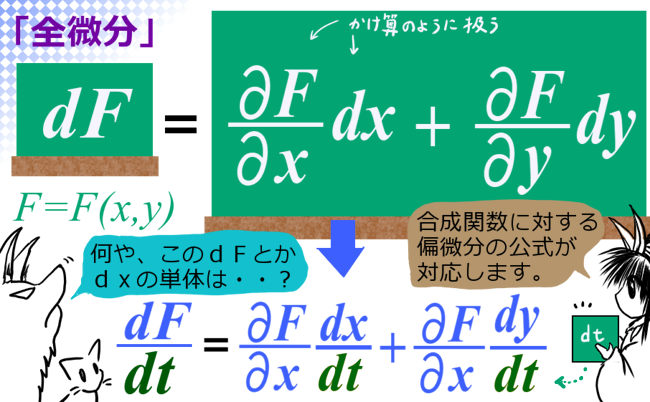
そこで、微分についても z=z(x,y) に対して次の関係があるわけです:
$$dz=\frac{\partial z}{\partial x}\frac{dx}{dt}dt+ \frac{\partial z}{\partial y}\frac{dy}{dt}dt $$
ここで、x、yによる偏微分は
「あたかも独立変数であるように、1つの変数のみで微分する」操作の意味です。
tによる微分の部分は、媒介変数が1つだけですので、
偏微分として書かなくてもよく通常の微分になります。
さて、となると、z=x+iy ですから、
$$ \frac{\partial z}{\partial x} =1,\hspace{10pt} \frac{\partial z}{\partial y} =i $$
となるので結局、
$$dz=\frac{dx}{dt}dt+ i\frac{dy}{dt}dt $$
という事になり、tで定積分を行う場合には1変数の合成関数の積分公式がそのまま使えて、結局xとyのそれぞれで積分して加えればよいという事です。
定積分においては、積分変数以外の変数は定数扱いで計算するとします。
もともとdz=dx+idyなので最初から積分する時には定積分を2つの部分の和にできると考えてもよいのですが、ここでは積分経路上でyとxには従属関係がある点に注意して説明をしておきました。
証明の計算
【グリーンの公式の証明】
さて、閉曲線上を経路として定積分する時にxとyに分けて定積分すればよいわけですが、ここでさらに、積分経路もxとyの各々について2つ以上に分けます。少なくとも4つの定積分を考える事がポイントです。
まずxについて。
閉曲線を切断するような、yが一定の直線分と、平面図上で閉曲線の上側の部分と下側の部分を考えます。この時、直線分に対して必ず上下に閉曲線の一部が対になって存在するようにします。このような閉曲線の分割を最低でも1つ行い、ものによっては2つ以上行います。
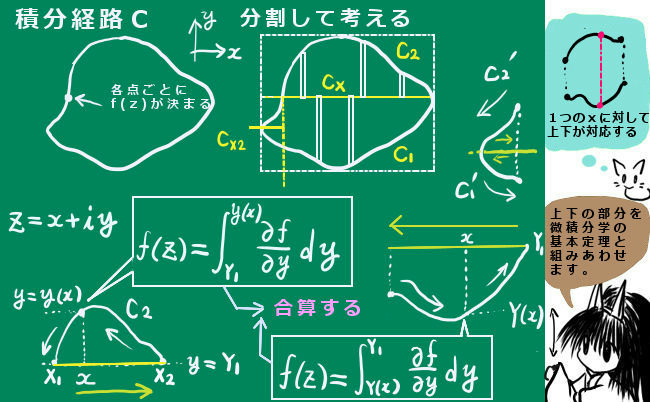
ただし、ここでは分かりやすくするために入れています。
ここで、f(z)=f(x,y)=f(x+iy) である事に注意します。まず「直線状の線分と閉曲線の下側の経路」(必ずしもつながってなくてもいい)で構成されるxによる定積分を、ぐるりと反時計周りに1周するように考えます。
$$\int_{C1}f(z)dx-\int_{CX}f(z)dx=\int_{X1}^{X2}f(x+iy)dx- \int_{X1}^{X2}f(x+iY_1)dx $$
$$=\int_{X1}^{X2} \left( – \int_ {y(x)}^{Y1} \frac{\partial}{ \partial y}f(x+iy)dy\right)dx = -\int_{X1}^{X2} \left(\int_ {y(x)}^{Y1} \frac{\partial}{ \partial y}f(x+iy)dy\right)dx $$
分割に使う直線分が2つ以上の場合も同様に定積分を考えておきます。
関数f(x,y)=f(x+iy) を、積分変数のみに着目した意味での(偏)導関数を定積分したものと考えるわけです。(プライスマイナスの符号に注意。)この考え方はベクトル解析などでも使います。
次に、 「直線分と閉曲線の上側の経路」で構成されるxによる定積分を、反時計周りに1周するように考えます。この時、直線部分は上記と同じものを共有してますが、積分の方向が逆です。曲線部分も積分の方向が逆なので符号が変わる点がポイントです。
$$-\int_{C2}f(z)dx+\int_{CX}f(z)dx=-\int_{X1}^{X2}f(x+iy)dx+\int_{X1}^{X2}f(x+iY_1)dx $$
$$= -\int_{X1}^{X2} \left( \int_{Y1}^{Y(x)}\frac{\partial}{ \partial y}f(x+iy)dy\right)dx $$
さきほどとは曲線が別のものになるので、y = y(x) ではなく y = Y(x) という形に書いて区別しています。
ここで、上記の2つのxについての「反時計回り」の定積分を加え合わせると、
$$\left( \int_{C1}f(z)dx-\int_{CX}f(z)dx \right)+ \left( -\int_{C2}f(z)dx+\int_{CX}f(z)dx \right) = \int_{C1}f(z)dx -\int_{C2}f(z)dx $$
$$= -\int_{X1}^{X2} \left( \int_ {y(x)}^{Y1} \frac{\partial}{ \partial y}f(x+iy)dy\right)dx -\int_{X1}^{X2} \left( \int_{Y1}^{Y(x)}\frac{\partial}{ \partial y}f(x+iy)dy\right)dx $$
$$= -\int_{X1}^{X2} \int_{y(x)}^{Y1} \frac{\partial f(x+iy) }{ \partial y}dxdy- \int_{X1}^{X2} \int_{Y1}^{Y(x)} \frac{\partial f(x+iy) }{ \partial y}dxdy $$
$$ =-\int_{X1}^{X2} \int_{y(x)}^{Y(x)} \frac{\partial f(x+iy) }{ \partial y}dxdy=-\int\int_D \frac{\partial f(x,y) }{ \partial y}dxdy $$
このように、もとの関数を(1つの変数以外は固定する意味で)偏微分したものの領域内に渡って重積分したものになるわけです。結果的にマイナス符号がついたのは「反時計回り」を考えた事に由来し、仮に「時計回り」を考えるならこの符号は逆になりプラスになります。xが変数の場合、右から左と、左から右に積分する場合では符号は逆になります。
上記のように重積分の形になると、それを「領域全体にわたって行う積分」とみなせます。
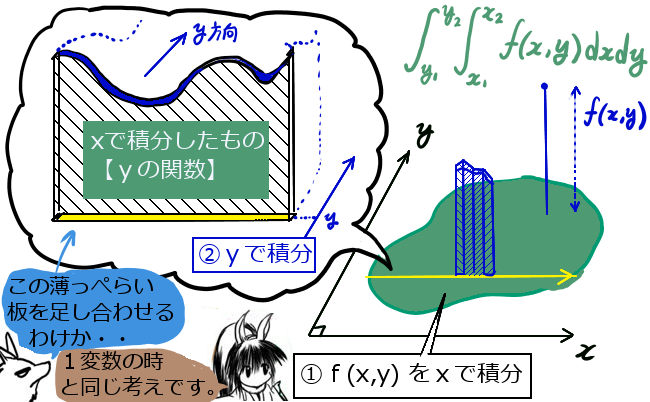
分割が2つ以上の場合でも、定積分を全て加え合わせて閉曲線が全てつながるようにします。(補助的に考えている直線状の線分の部分は、分割がいくつであっても全てプラスマイナスが打ち消し合って定積分の合計は0になります。)
今度は、yについての定積分についても同じ事をやります。途中の計算は全く同じなので少々省きますが、次のようになるのです。
$$\left( \int_{C3}f(z)dy-\int_{CY}f(z)dy \right)+ \left( -\int_{C4}f(z)dy+\int_{CY}f(z)dy \right) = \int_{C3}f(z)dy -\int_{C4}f(z)dy $$
$$ =\int_{Ya}^{Yb} \int_{x(y)}^{X(y)} \frac{\partial f(x+iy) }{ \partial x}dxdy=\int\int_D \frac{\partial f(x+iy) }{ \partial x}dxdy $$
yのほうには i を添えたうえで、得られた結果を合わせると次のようになります。
$$ \int_{C1}f(z)dx -\int_{C2}f(z)dx + i\int_{C3}f(z)dy -i\int_{C4}f(z)dy $$
$$= \int\int_D \left( – \frac{\partial }{ \partial y} +i\frac{\partial }{ \partial x} \right) f(x+iy) dxdy= \int\int_D \left( i\frac{\partial }{ \partial x} – \frac{\partial }{ \partial y} \right) f(x,y) dxdy $$
分割した部分がxとyについて合わせて4つを超える場合でも同じで、全て加え合わせます。
再びdz=dx+ i dyに戻ると、閉曲線C上で反時計周りに定積分を行う場合は次のようになります。
$$\int_Cf(z)dz=\int_Cf(x,y)dx+i\int_Cf(x,y)dy$$
$$= \int_{C1}f(z)dx -\int_{C2}f(z)dx + i\int_{C3}f(z)dy -i\int_{C4}f(z)dy $$
分割の部分が多い場合も同様です。もとの閉曲線の曲線部分が全て入るようにします。
xについては、左→右:+符号 右→左:逆で-符号
yについては下→上:+符号 上→下:-符号 として部分ごとに定積分を対応させます。
これによって、結局公式の通りの関係式が成立する事になります。
$$ \int_Cf(z)dz=\int_Cf(x,y)dx+i\int_Cf(x,y)dy = \int\int_D \left( i\frac{\partial }{ \partial x} – \frac{\partial }{ \partial y} \right) f(x,y) dxdy 【証明終り】$$
参考:長方形による近似を使う証明の方法
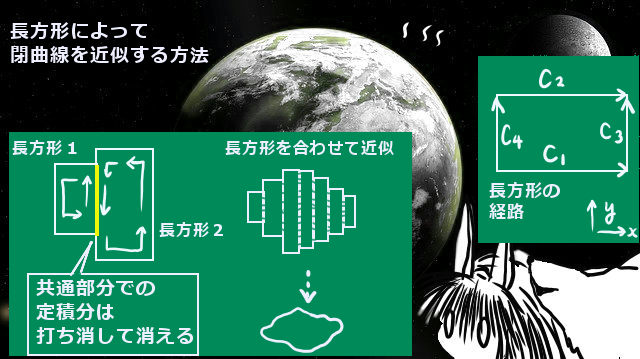
参考までに、積分経路として小さな「長方形」を考えて、これの合計として任意の閉曲線を経路とする時も成立するという証明の仕方もあります。
こちらの考え方だと、長方形ですので最初からxのみ、yのみという考え方が使えて、積分の計算がらくです。積分の方向を反時計回りという事で決めておけば、ぴったり隣り合う長方形同士の接する辺同士は積分が打ち消し合って周囲だけの分が経路として残るというわけです。
ただしこの方法の場合、じつは経路自体の形が「長方形 → 任意の(滑らかな)閉曲線」に移行する段階の時の話が少し面倒です。実際、円のような曲線を多角形で近似するような事は珍しくありませんが、「長方形」で近似するという事は、他の数学の分野ではあまり多くやらない事かと思います。一般の多くの複素関数論の教科書では、この詳細をあまり書きたがらない傾向があるように思います。
本質的には上記で述べた証明方法と比べて、やる事はそんなに変わりません。
前述の通り、複素関数論におけるグリーンの公式は、コーシーの積分定理に結びつく事で、さらなる積分の理論を組み立てる事に使われていきます。